机载布撒亚音速子弹药初始外弹道性能研究
王 尧,毛 亮,何 筱,魏晨杨,祁宇轩,姜春兰
(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
1 引言
先进的机载布撒武器作为一种防区外发射、精确制导的空对面武器系统,可携带各种不同类型的子弹药对目标进行攻击,在现代战争中扮演越来越重要的角色[1]。子弹药抛撒出舱后,为了获得理想的弹道条件,通常在弹体尾部会加装降落伞来进行调姿转向;而为了能获得理想的落点分布,子弹药通常会控制不同的延时开伞时间。机载布撒武器为了实现较高的效费比,子弹药一般都是无控的,属于非制导类子弹药。因此,在子弹药降落伞打开之前(即外弹道初始阶段),能否保证子弹药飞行的稳定性,对于实现最终毁伤目的尤为关键[2-3]。子弹药弹体结构特征是影响子弹药气动特性及飞行稳定性的重要因素。
Josyula等[4]采用不同格式模拟了超音速弹丸周围的绕流行为,结果表明,采用中心差分格式和迎风差分格式进行计算,分别在涡流和横流的模拟中具备精度优势。冯顺山等[5]模拟了尖拱圆柱形弹周围绕流在大攻角范围内的行为,将弹体绕流模拟攻角范围拓展至±180°。Jason Wang[6]使用任意拉格朗日-欧拉ALE(arbitrary lagrangian-eulerian,ALE)方法对减速伞流场行为进行了计算分析,将气动性能计算从刚体弹丸延伸到柔性体减速伞。Jubaraj等[7-9]基于流体动力学-刚体动力学CFD-RBD(computational fluid dynamics-rigid body dynamics,CFD-RBD)方法建立了超音速尾翼弹、旋转制导弹药等多种复杂结构飞行体的精确空气动力学模型,计算结果与试验结果较吻合。Harris等[10]在CFD-RBD方法基础上加入碰撞预测模型,对大批量子弹药分离过程进行了预测,将CFD-RBD方法拓展至了多体在复杂流场中的交互行为。钟阳等[11]基于任意拉格朗日-欧拉形式的流动模型,改进了高速旋转弹丸的CFD-RBD耦合模型,解决了传统方法或者不能直接用于研究弹丸的自由运动,或者远场计算不准确的问题。许伟[12]设计了机载布撒器抛撒系统,计算了子弹药的运动规律和散布落点,提出了抛撒弹道应满足的各项要求。毛亮等[13]采用MonteCarlo计算了单发机载布撒器对机场跑道的封锁效率受攻击角、随机扰动和风场的影响规律,基于质点弹道评估了子弹药外弹道性能。
总体而言,目前针对机载布撒武器子弹药外弹道性能计算的技术手段较为完备,针对某一种弹型的全弹道分析也较为普遍,但针对亚音速投放条件下弹体结构特征对其初始外弹道性能的影响研究较少,且局限于单纯分析弹体受力,未对流场行为描述分析。本文中主要针对几种常见的弹体头部和尾翼结构的气动力特性进行了数值仿真,通过分析弹体绕流行为,得到弹体气动外形与气动参数改变的内在联系,并结合仿真气动力参数和6自由刚体外弹道模型对其初始外弹道性能进行了计算分析,研究结果可为机载布撒子弹药的相关设计提供一定参考。
2 气动力仿真方法和外弹道模型
2.1 气动力仿真方法
2.1.1有限元仿真模型
子弹药飞行过程中的周围流场通常表现为层流-湍流共同作用的非定常流动,本文中,采用Fluent计算流体力学软件对长径比为3.7的无控尾翼式子弹药在攻角分别为0°、2°、4°、6°、8°时,0.72Ma亚音速来流下的气动力特性进行数值计算,将弹体视为刚性流场边界,通过建立流场网格得到其对弹体的作用力[14]。
子弹药弹体头部外形包含:平头、圆头与凹头,尾翼构型设置有6片尾翼和8片尾翼(二者总翼展面积一样),此外,在平头6片尾翼弹的头部增加了一个突起结构(主要用于目标探测)。具体计算模型如图1所示。

图1 子弹药计算模型
有限元模型如图2所示,流场大部分设置为四面体 Euler网格,在弹体表面设置四层膨胀网格,并进行局部网格细化。

图2 流场有限元仿真模型
2.1.2控制方程
将求解器设置为基于密度(density-based)的稳态(transient)模式。由于在亚音速条件下气体压缩不可忽略,将“energy”选项调至“on”。
流场湍流控制选择“Spalart-Allmaras”,流场材质选择“ideal gas”。流场粘度控制方程选择Sutherland模型。流场边界设置为无穷远处压力远场边界条件[15]。
求解策略选择显式(explicit)求解,通量格式选择“Roe-FDS”。空间离散方式中,梯度选择“Least Squares Cell Based”,层流、湍流动能和比能量耗散率均选择“Second Order Upwind”。根据试运行模型收敛情况将松弛系数设置为0.8。
2.2 外弹道计分析模型
2.2.16自由度刚体弹道模型
将子弹药视为刚体,在无风以及攻角较小条件下,建立6自由度刚体弹道模型,包含子弹药在6个自由度上的动力学与运动学关系共12个方程,以及弹轴坐标系与速度坐标系几何关系共3个方程。
(1)
式(1)中:x2、y2、z2角标代表速度坐标系三方向;ξ、η,ζ角标代表弹轴坐标系三方向;t为时间;m为弹体质量;A、C为弹体径向和轴向的转动惯量;v为弹体飞行速度;x、y、z为弹体空间位置坐标;θa、ψ2为速度坐标系与地面坐标系两方向上的夹角;φa、φ2为弹轴坐标系与地面坐标系两方向上的夹角;γ为弹体绕轴自转角;ω为弹体在弹轴坐标系中的角速度;F为弹体在速度坐标系中的受力;M为弹体在弹轴坐标系中所受的力矩;δ1、δ2、β为弹体飞行攻角和坐标系中间计算变量。求解此微分方程组,即可得到弹体飞行过程中弹道诸元变化情况。
2.2.2基于龙格-库塔法的弹道模型解析
龙格-库塔法是一种常微分方程数值解法,这一方法的优点在于计算精度高、程序简单、改变计算步长容易,可以自启动[16-17]。其中,4阶龙格-库塔法最为常用,其表述如下。
对含有m个函数yi的常微分方程组,表示为:
(2)
其具备初值为:
yi(t0)=yi0(i=1,2,…,m)
(3)
若已知其在t=tn时刻的取值yi,n,则其在下一时间步的取值为:
(4)
式(4)中各取值为:
(5)
由式(5)分析得到,常微分方程组下一个时间步的取值yi,n+1由现在时间步取值加上时间步步长h与估算斜率k的乘积所决定。而k为以下4个斜率的加权平均:k1是时间段开始时的斜率,k2是时间段中点的斜率,其函数值通过欧拉法采用斜率k1得到,k3也是时间段中点的斜率,但是其函数值通过欧拉法采用斜率k2得到,k4是时间段终点的斜率,其函数值由k3决定。
采用龙格-库塔法对6自由度刚体弹道模型进行求解,在输入初始弹道诸元和规定时间步以后,此方法可以以任意循环数计算每一个时间步时的弹道诸元。
3 弹体结构对流场行为和气动特性的影响
3.1 头部突起对流场行为与气动特性的影响
图3给出了来流流经有无头部突起2种弹型时的流场行为。

图3 头部突起对流场影响(δ=0°)
从图3可看出,弹体绕流受突起影响较小,弹侧湍流区和弹底低速区的规模,在有无突起时其区别不大。引入突起会在突起头部和侧面引入一片高速区,由于这一高速区规模较小,对弹体所受气动阻力的影响较小。由于突起的引入使弹体失去对称性,这一高速区对弹体所受气动升力和静力矩有一定影响。
表1给出了不同攻角时有无突起情况下子弹药的气动系数。

表1 有/无突起时弹体气动系数Table 1 Aerodynamic characteristics with/without head-rod
计算得到,未引入头部突起情况下,子弹药升力系数导数(对弧度制攻角的导数,下同)为7.40,静力矩系数导数为1.84;引入头部突起后,升力系数导数为5.76,静力矩系数导数为1.43。
可以看出引入突起对弹体阻力系数几乎无影响,会使得升力系数导数减小为无突起时的77.8%,静力矩系数减小为无突起时的77.7%,由于上述比例数值接近,分析认为引入头部突起对子弹药所受气动力压心位置影响较小。
3.2 头部外形对流场行为与气动特性的影响
图4给出了平头、圆头及凹头等3种弹型在攻角δ为0°的来流中的流场行为(以速度流线为例)。
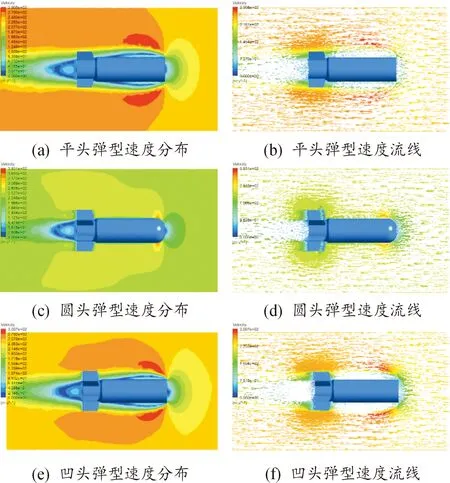
图4 头部外形对流场影响(δ=0°)
从图4可以看出,弹体所受气动阻力主要是头部流场速度骤减形成的高压区、弹体周围裹挟的气流对流场的阻碍作用以及尾部低速低压湍流这三者的共同作用。
弹头前方的来流在弹头阻碍下加速从头部边缘经过,从弹体头部边缘开始在弹身周围外层形成了高速层流区;在高速区的内部弹身周围内层存在速度近乎为零的低速附着湍流区,表现为弹体“裹挟”了气团;在弹底后方出现了低速湍流区,尾部直径缩小区域和尾翼后侧形成了规模较小的湍流。弹体周围“膨胀”的湍流“挤压”形成了外层高速气流,从这个角度上也可以视作弹体周围的低速附着层,增加了弹体直径的大小。
对平头弹型和凹头弹型,可以看出其头部高速区边缘非常清晰,边缘与弹体所形成的夹角也较大,这一高速区甚至延伸至弹底尾翼外侧,在尾翼附近形成了一定的高速区域。而在弹身周围的低速附着层,体积十分明显,就截面而言,其几乎将弹体半径增加1倍。
而对圆头弹型而言,其头部高速区边缘较为模糊,仅在圆头与弹身连接处有一定的“挤压”,生成了高速气流,但规模也较小。弹体四周几乎没有静滞气流。流体几乎以层流的形式流经弹身,这使得尾翼所受来流更为稳定,故围绕尾翼的流线也更稳定。表2给出了不同攻角下各头部外形弹型的气动系数。
通过计算可知,对平头弹型,子弹药升力系数导数为7.40,静力矩系数导数为1.84;对圆头弹型,升力系数导数为6.80,静力矩系数导数为0.86;对凹头弹型,升力系数导数为5.47,静力矩系数导数为1.84。
图5为不同头部外形弹丸的气动力系数随攻角的变化曲线。

表2 各头部外形弹体气动参数Table 2 Aerodynamic characteristics of different head shapes

图5 头部外形对弹体气动系数的影响
从表2和图5可以看出,圆头弹型阻力系数几乎不随攻角变化而变化,其数值约为平头弹形的31.4%。平头弹型和凹头弹型阻力系数接近。圆头弹型的升力系数关于攻角的导数约为6.8,由于气动力压心更加接近弹体中心,其静力矩系数导数仅为0.86,为平头弹形的46.7%。
由于流经圆头的气流更加倾向于层流,其对尾翼的阻力也更稳定,圆头弹型表现出更好的稳定性,其静力矩系数与攻角变化表现出较好的线性相关,而其他2种弹型在攻角较大时,其静力矩系数变化的线性变差。
3.3 尾翼构型对流场行为与气动特性的影响
由于尾翼是弹丸产生气动升力的主要部件之一,仅通过攻角δ为0°时的流场难以全面地反映尾翼外形和数量改变的影响。
图6、图7分别给出了6片尾翼与8片尾翼2种弹型在攻角δ为8°来流中的流场行为(以速度流线为例)。
在图6中,尾翼不同的2类弹形的头部速度分布并没有产生明显区别,而弹身侧面附着的低速湍流区体积也大致相同。结合第3.2节中对流场行为的分析,认为尾翼数量对弹体所受气动阻力影响不大。
此外,尾翼不同的2类弹型在迎风面上的速度分布差距并不明显,而在背风面(即图6中下方)存在着较明显的差异。以图6(c)、图6(d)为例,6片尾翼弹型的背风面尾翼处并未形成大规模的高速流线团簇,而8片尾翼弹型的背风面尾翼处明显有一团高速气流附着。这说明6片尾翼弹型的尾翼对来流起到了更好的阻碍效果,来流经过尾翼后大部分气体速度明显降低,而八尾翼弹型的尾翼对来流的阻碍效应就不那么显著了。分析认为8片尾翼弹型相对会受到更小的气动升力。

图6 尾翼构型对平头弹型流场影响(δ=8°)

图7 尾翼构型对圆头弹型流场影响(δ=8°)
分析对比图6、图7,可以看出,头部外形在攻角较大时对尾部流场的影响也较为明显,由于平头弹型头部对气流的阻碍作用较强,经过头部后气流的湍流性较强,放大了尾翼的作用,平头弹型在大攻角下尾部流场出现了明显的沿气流方向偏移,而圆头弹型在大攻角下尾部流场几乎关于弹轴对称,后者受到的弹体四周裹挟低速气流区的后续作用更小。表3给出了不同攻角下各尾翼构型的气动系数。
计算得到,对平头弹型,6片尾翼时子弹药升力系数导数为7.40,静力矩系数导数为1.84,8片尾翼时升力系数导数为7.26,静力矩系数导数为1.08;对圆头弹型,6片尾翼时升力系数导数为6.80,静力矩系数导数为0.86,8片尾翼时升力系数导数为5.80,静力矩系数导数为0.50。
各尾翼构型弹型的气动系数如图8所示。

表3 各尾翼构型弹体气动参数Table 3 Aerodynamic characteristics of different wings

图8 尾翼构型对弹体气动系数的影响
相对于6片尾翼的方案,8片尾翼的弹型在阻力系数上几乎没有差距,在升力系数上差距亦不大,而在静力矩系数上有较明显的降低,无论是平头还是圆头,8片尾翼弹型静力矩系数导数约为6片尾翼弹形的58%。对尾翼的选择需要结合实际工程上对弹体气动参数的需求而决定。
4 子弹药初始外弹道飞行稳定性分析
4.1 稳定储备量分析
对于尾翼稳定弹而言,静稳定储备量是评估子弹药气动稳定性的重要参数。对普通无控尾翼稳定弹的稳定飞行需求而言,根据工程经验,通常需要其静稳定储备量在10%~30%[18],如静稳定储备量过大,会使得弹体对风和其他扰动产生过度反应,也会增大振动频率,而稳定储备量过小则会使得弹体容易失稳,攻角不易收敛。表4给出了不同弹体头部外形和尾翼特征子弹药的静稳定储备量。

表4 各种弹型的稳定储备量Table 4 Stability storage of projectiles
从表4可以看出,除了凹头6片尾翼和圆头8片尾翼弹型外,其余弹型的稳定储备量均在工程经验范围内。凹头6片尾翼子弹的稳定储备量较大,而圆头8片尾翼子弹的稳定储备量较小。分析认为这是由于凹头6片尾翼弹型尾部流场湍流性质最强,其气动力压心相对最靠后,而圆头8片尾翼弹型尾部流场层流性质最强,其气动力压心相对最靠前。
4.2 弹体外形对攻角收敛的影响
实际抛撒过程中,由于子弹药侧向飞离布撒器时弹体方向仍与布撒器保持一致,使得子弹药初始弹道诸元即存在一定的攻角。上述初始侧向攻角,以及弹体由于重力下落产生的俯仰攻角,以及其他随机扰动产生的随机攻角,共同构成了弹体在全弹道过程中的总攻角。这一攻角能否稳定保持在一个较小范围内,是判断子弹药飞行稳定性的标准。
计算初始弹道诸元为:牵连速度vx=240 m/s、侧抛速度vz=12 m/s,初始攻角为δ0=0.05 rad,取大气密度ρ=1.226 kg/m3、重力加速度g=9.801 m/s。忽略随机扰动,将弹体气动特性近似视为线性,通过将前述各弹型气动特性代入6自由度刚体弹道模型,可以得到各弹体外形下攻角收敛情况,如图9所示。
从图9可以看出,各弹体外形均能在初始外弹道飞行时攻角快速收敛。头部外形中,收敛周期由短到长依次为:平头<凹头<圆头,单周期收敛幅度由小到大依次为:圆头<平头<凹头。6片尾翼弹型较八尾翼弹型攻角收敛周期更短、但单周期收敛幅度也更小,总体而言,凹头弹型和6片尾翼弹型收敛更快。这与第4.1节结论中,凹头6片尾翼子弹的稳定储备量33.6%为各弹型中最大相符。

图9 弹体外形对攻角收敛影响
4.3 非气动因素对攻角收敛的影响、
实际工程情况中,由于弹药结构设计不同,其自身质量及径向转动惯量会存在差异。
图10、图11给出了不同子弹药质量和径向转动惯量条件下,子弹药在初始外弹道飞行阶段的攻角收敛情况。

图10 弹体质量对攻角收敛影响

图11 弹体径向转动惯量对攻角收敛影响
由图10可以看出,当弹体质量增大时,子弹药在一个攻角震荡周期中收敛的幅度基本不变,同时其攻角振荡周期略有缩短。分析认为子弹药质量对初始外弹道飞行稳定性的影响较小。
由图11可以看出,当径向转动惯量增大时,子弹药在一个攻角振荡周期中收敛的幅度基本不变,同时其攻角振荡周期明显延长。分析认为,径向转动惯量对初始外弹道飞行攻角收敛速度的影响较大,增加径向转动惯量对子弹飞行过程中飞行稳定性较为不利。
5 结论
基于CFD对不同弹体结构在亚音速流场下的气动特性进行数值仿真分析,并基于龙格-库塔法求解了6自由度刚体外弹道模型,主要结论如下:
1) 亚音速流场中,弹体周围附着的低速湍流区大小是决定弹体所受空气阻力的重要因素。弹体头部突起基本不影响弹体所受气动阻力;圆头弹型阻力系数和静力矩系数导数为0.349和0.86,相应为平头弹型的31.4%和46.7%;在总翼展面积相同时,增加尾翼数量会减小弹体所受气动升力,8片尾翼弹型的静力矩系数为6片尾翼弹形的58%。
2) 除了凹头6片尾翼和圆头8片尾翼弹型外,其余弹型的稳定储备量均在工程经验范围10%~30%;凹头6片尾翼子弹的稳定储备量较大,而圆头8片尾翼子弹的稳定储备量较小;分析认为其原因是弹体绕流的层流/湍流行为不同导致的气动力压心位置变化。
3) 各弹体外形均能在初始外弹道飞行时攻角快速收敛。头部外形中,收敛周期由短到长依次为:平头<凹头<圆头,单周期收敛幅度由小到大依次为:圆头<平头<凹头;6片尾翼弹型较8片尾翼弹型攻角收敛周期更短、但单周期收敛幅度也更小,总体而言,凹头弹型和6片尾翼弹型收敛更快。非气动因素中,弹体质量对初始外弹道攻角收敛影响较小,而当径向转动惯量增加时,会显著增加攻角收敛的周期长度。

