基于Sage-Husa自适应滤波的快速系统级标定方法

赵桂玲，谭茂林，姜子昊

(辽宁工程技术大学 测绘与地理科学学院， 辽宁 阜新 123000)

1 引言

捷联惯导系统的核心是由3个加速度计和3个陀螺仪组成的惯性测量单元(inertial measurement unit，IMU)，其主要误差为零偏误差、标度因数误差、安装误差、随机噪声[1-2]。IMU的误差对导航精度会产生很大影响，并且随时间累积，因此必须对其进行标定和补偿,以提高实际应用中系统的导航精度[3-5]。

在系统级标定滤波法中，IMU误差参数作为状态量，通过构建Kalman滤波器将其估计出[6]。文献[7-10]构造不同的误差模型、设计标定路径，通过Kalman滤波来估计IMU误差参数。文献[11]使用强跟踪滤波(strong tracking filter，STF)来估计IMU零偏误差和标度因数误差。文献[12]提出一种甲壳虫群须搜索(beetle swarm antenna search，BSAS)算法，通过设计24个测量位置标定出三轴加速度计零偏误差、标度因数误差、安装误差和加速度计二次项误差共计15项误差参数。文献[13]结合模型预测滤波和Sage-Husa自适应滤波，提出一种自适应模型预测组合滤波算法用于在线标定，标定出IMU标度因数误差和零偏误差共10项误差参数。文献[14]设计一种基于新息自适应滤波方法在线标定方案，克服常规Kalman滤波需预先设置噪声的不足，标定出24项IMU误差参数。在系统级标定中，是否可以引入新的滤波算法？以提升滤波收敛精度或收敛速度。

本文提出一种基于Sage-Husa自适应滤波的系统级标定方法，对系统中量测噪声方差阵进行自适应处理。对噪声进行自适应处理的效果与系统的可观测性强度有一定关系[15-16]，将标定模型降维，设计中间参数对误差参数项进行合并，得到12维的可观测性高的滤波模型。采用6个静态位置进行标定实验，利用得到的每个静态标定位置下中间参数滤波收敛结果进行解耦计算，最终成功标定出24项IMU误差参数。仿真实验表明，相较于常规Kalman滤波系统级标定，本文中提出的方法在滤波收敛速度更快，可节省标定所需时间。

2 Sage-Husa自适应滤波算法

Kalman滤波是一种最优估计技术，根据系统量测量估计系统的状态量[17]。系统状态空间模型由状态方程和观测方程组成，设离散化后的状态方程和量测方程为：

(1)

式中:k为离散时间；Xk为k时刻的状态向量；Φk|k-1为k时刻到k-1时刻的状态转移矩阵；Γk-1为系统噪声矩阵；Wk-1为系统噪声；Zk为量测向量；Hk为量测矩阵；Vk为量测噪声。

应用Kalman滤波时，一般要求Wk和Vk互不相关，且均为零均值白噪声。离散系统标准Kalman滤波由5个基本公式构成，如下：

1) 时间更新方程

(2)

(3)

2) 量测更新方程

(4)

(5)

Pk=(I+KkHk)Pk|k-1

(6)

常规Kalman滤波只有在随机动态系统结构参数和噪声统计特性参数都准确已知的条件下,才能获得状态的最优估计[18]。在使用常规Kalman滤波时，对噪声协方差阵进行经验设定，即系统噪声方差阵Qk和量测噪声方差阵Rk被设定为固定不变的经验值，滤波的状态估计结果将受到影响[19]。自适应滤波对噪声进行实时估计和更新，能够减小滤波器对先验信息的依赖，有助于提升滤波状态估计效果[20]。文献[21]提出一种基于Sage-Husa滤波渐消因子选择的陀螺在线标定方法，在外部环境变化情况下，对比常规Kalman滤波，该方法在标定时间和标定精度上更能有效地估计出陀螺零偏误差和标度因数误差。文献[22]利用Sage-Husa自适应滤波对捷联惯导系统进行初始对准，实验结果表明，相对常规Kalman滤波，自适应滤波在收敛时间上优势明显。

自适应滤波要解决的主要问题是估计Qk和Rk。Qk与系统特性有关，不易发生改变。量测噪声由外部因素引起，容易发生较大变化，设定固定不变的Rk可能对收敛时间和收敛精度造成影响[15,23]。因此为准确掌握量测噪声方差阵Rk的特性，以提升捷联惯导系统级标定的效果，引入Sage-Husa自适应Kalman滤波，对系统中Rk进行估计和更新。Sage-Husa自适应Kalman滤波的Wk和Vk满足下式：

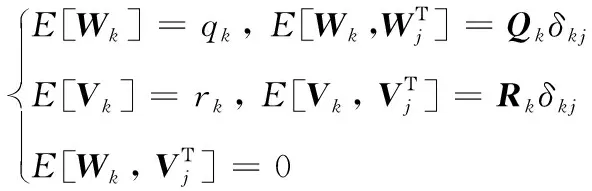
(7)

式中:qk、rk、Qk、Rk为噪声参数;δkj为克罗尼克函数。

本文中提出的Sage-Husa自适应滤波方法，是在常规Kalman滤波的基础上，对量测噪声方差阵Rk进行估计，计算更新形式如下：

(8)

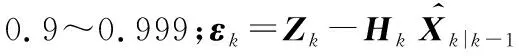
图1 Sage-Husa自适应滤波计算流程

3 降维模型的建立

对IMU零偏误差、标度因数误差和安装误差这3种主要误差进行研究，IMU误差参数模型可写为：

(9)

静基座下IMU误差与速度误差和姿态误差的关系为：

(10)

结合式(9)，式(10)进一步可以写为：

(11)

根据系统误差方程(11)建立滤波模型，模型维数为30维。由于自适应滤波算法的处理效果与系统可观测强度存在关系，减少模型维数，有利于增强自适应滤波的有效性。将IMU误差参数先进行合并，引入6个中间参数如下：

(12)

(13)

将式(12)和式(13)代入误差方程(11)有：

(14)

于是，滤波器的维数由原来的30维降为12维，模型的可观测强度有了很大的提升，滤波器状态向量如下：

(15)

根据式(11)和式(14)，滤波器的状态方程为：

(16)

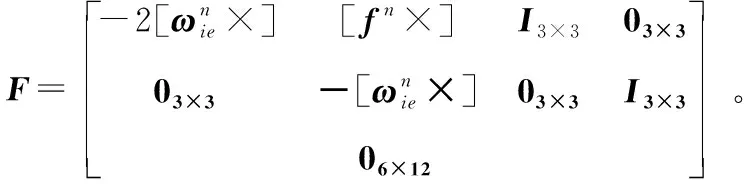
滤波器的量测方程为：

Z=HX+V

(17)

设计6个静态标定位置，标定路径示意图如图2所示。

图2 6位置标定路径示意图

通过滤波算法可以得到每个静态标定位置下中间参数的收敛结果，即得到6个滤波收敛结果为e1-j～e6-j(j表示标定位置，j=1,2,…,6)。

将每个静态标定位置代入系统速度误差和姿态误差方程中，可得到每个位置下中间参数和待标定误差之间的关系。例如将位置1(东北天)代入公式(14)有：

(18)

式(18)为位置1下中间参数与待标定IMU误差参数的数学关系。通过6个标定位置下中间参数与待标定参数的数学关系组，进一步进行解耦计算，最终解得待标定误差参数数值，实现了IMU误差参数的全标定。

4 仿真实验

为验证本文中提出的基于Sage-Husa自适应滤波的系统级标定方法的有效性，对比常规Kalman滤波分别开展仿真实验，IMU误差参数预设值见表1和表2。各位置下IMU标定仿真时间设置均为10 min，其中为使得与加速度计有关的3个中间参数在2种滤波下的比较更为明显，与加速度计相关的滤波估计曲线截取标定时间内第0～1 min进行展示。6个静态标定位置下的滤波估计曲线如图3—图8所示。

图3 位置1下2种滤波估计曲线

图4 位置2下2种滤波估计曲线

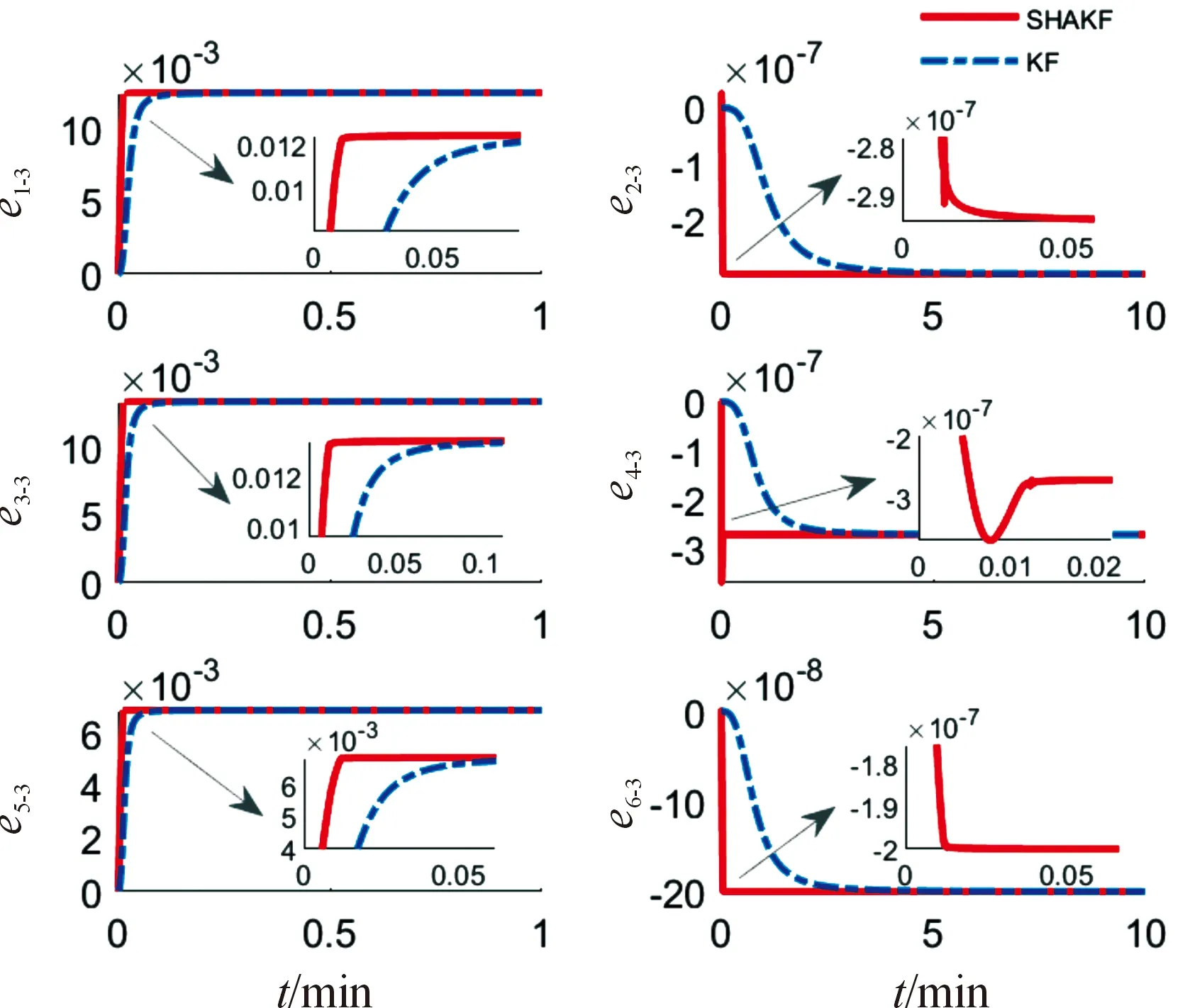
图5 位置3下2种滤波估计曲线

图6 位置4下2种滤波估计曲线

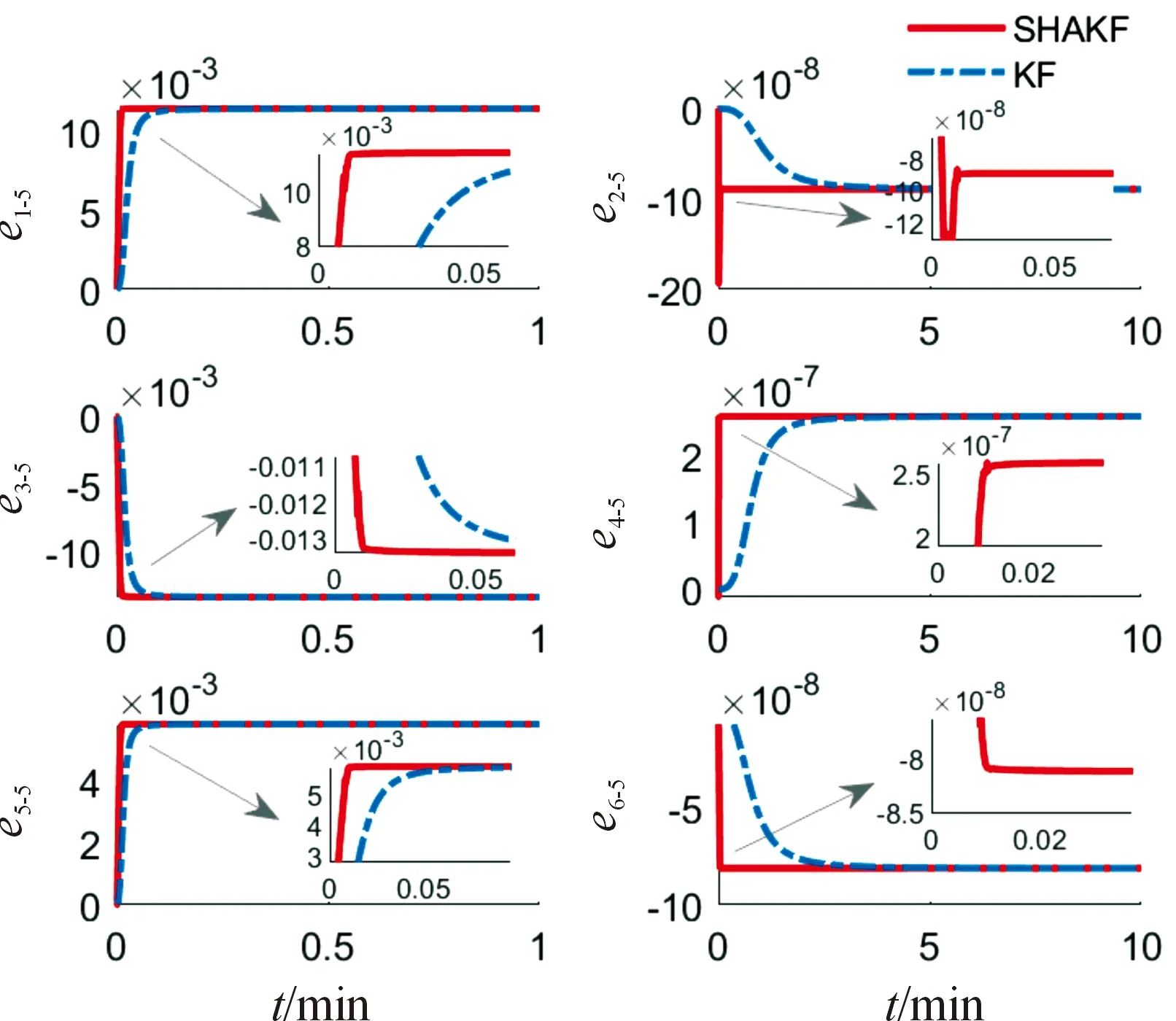
图7 位置5下2种滤波估计曲线

图8 位置6下2种滤波估计曲线

根据6个位置下滤波收敛结果，进一步完成解耦计算，得到IMU误差参数的标定结果如表1和表2所示。

表1 加速度计误差参数标定结果Table 1 Acceleration error parameter calibration results

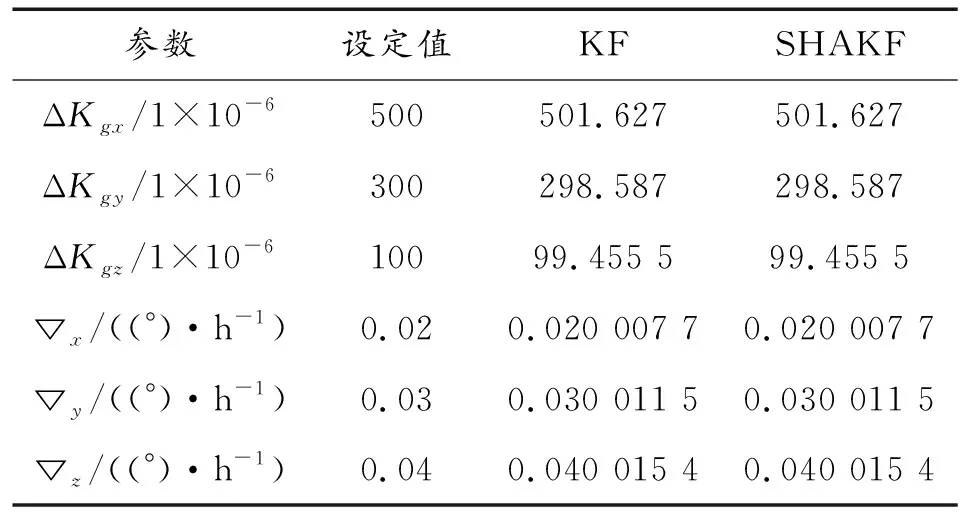
表2 陀螺误差参数标定结果Table 2 Gyro error parameter calibration results

从图3—图8的6个静态标定位置下的滤波估计曲线可看出，中间参数在每个静态标定位置下滤波均有较好的收敛结果。根据表1和表2的标定结果可知2种方法的相对误差均小于0.6%，2种方法在标定精度上相当。相较于常规Kalman滤波(对应图中KF)，本文提出的Sage-Husa自适应滤波算法(对应图中SHAKF)的收敛速度更快。在与陀螺有关的中间参数滤波收敛上，Sage-Husa自适应滤波算法优势十分明显，常规Kalman滤波需要大约5 min才能满足收敛条件，而Sage-Husa自适应滤波算法仅6 s即满足了收敛条件。

5 结论

本文所提出的标定方法对降低捷联惯导系统级标定时间具有一定的参考价值，仿真结果表明：系统级标定采用常规Kalman滤波算法，将量测噪声方差阵设定为固定值，使得滤波收敛速度慢。采用Sage-Husa自适应滤波对量测噪声方差阵进行实时估计和更新，能有效降低标定时间。与常规Kalman滤波相比，标定精度相当，均小于0.6%；滤波收敛速度有显著提升，标定时间由5 min缩短至6 s，缩短了98%。