基于Scanlan颤振导数理论求解水翼临界颤振状态
魏子天,洪 亮,刘新月,南 栩
(1.中国船舶科学研究中心国家船舶噪声与振动重点实验室,江苏 无锡 214000;2.南京理工大学 能源与动力工程学院, 南京 210000)
1 引言
水翼是船舶上调整航向的结构,水翼处在密度较大的水流中,水流会对水翼产生非定常激励从而导致水翼振动。近年来造船技术飞速发展,船舶航行速度越来越高。在高流速下,一种特殊的振动“颤振”愈发引起研究者的注意,颤振是结构阻尼无法消耗流场的输入能而导致振幅不断扩大的振动。颤振最早发现于航空器,早期航空器多采用展弦比较大的机翼,颤振现象频发,对于机翼颤振的研究也较多,现阶段水翼颤振的相关研究也多由空气动力学领域的相关理论改进而来。
目前常用的颤振预测方法有ONERA失速气动力模型,展志焕等[1]基于该模型,建立二元翼型的非线性颤振运动的方程,获得非线性颤振时域响应曲线,由二分法寻找翼型的临界颤振状态。在发生颤振时机翼气动力具有非线性,赵永辉等[2-3]使用该模型对三维弯扭耦合梁进行了失速攻角下的颤振状态分析。此外,Theodorsen[4]提出的基于非定常气动力线性化精确解的Theodorsen非定常气动力模型应用也较多,刘胡涛[5-6]由该理论的理论解求解水翼算例的水弹性不稳定边界条件,并使用龙格-库塔法进行了验证。李景奎等[7]使用V-g法对气动弹性运动方程的特征值进行求解,获得机翼的临界颤振速度。在试验方面,Song[8]采用实验的方法,对三维机翼上的非定常水动力及其水动弹性特性进行了实验测定。并通过水洞试验对不同机翼的颤振速度进行预测。Jewell[9]在美国的戴维-泰勒拖曳水池,通过设置2个自由度弹簧系统,以结构阻尼比为变量做了大量关于水翼颤振的试验。
对于水翼颤振的研究理论仍较为匮乏,本文引入桥梁振动领域应用较多的“Scanlan颤振导数理论”,使用CFD模拟的方法,根据理论求取水翼的颤振导数,进而求得水翼的临界颤振状态,最后采用非线性振动求解方法纽马克-β法对求得的结果进行验证与分析。
2 水翼计算模型
采用二维模型进行计算,选取单位长度的水翼节段,设定水翼有沿着翼展方向“竖弯”方向运动自由度,以及沿旋转轴转动的“扭转”自由度,将这2个自由度方向上的运动进行结合,来表达二维水翼的振动情况。2个自由度上的运动由弹簧-阻尼系统进行控制,如图1所示。
使用NACA0015翼型,水翼弦长b=0.35 m,攻角为0°。水翼的竖弯及扭转2个方向上水翼的固有频率分别为ωh=4.37 Hz及ωα=2.95 Hz。水翼每延米的质量为m=206 kg,扭转惯性矩为Im=12.11 kg·m2/m。刚心设置在距离水翼前缘0.42倍弦长处,与水翼的重心位置重合。

图1 2个自由度模型
应用Fluent软件进行计算。水翼的振动涉及到边界的运动,需要用到“动网格”,本文采用Fluent前处理软件ICEM进行建模和网格划分,网格使用“刚性边界层运动区域+动网格变形区域+外流场”的划分策略。图2给出了网格划分的大致示意图。流场网格如图3所示,水翼前、后缘网格如图4所示。

图2 网格区域示意图
图2中,A区域为刚性运动区域,该区域与水翼一起运动。该区域的半径为b,采用四边形结构化网格划分,以保证水翼运动时计算的收敛性。B区域为动网格区域,采用了三角形非结构化网格进行划分。该区域的网格更新策略为“Smoothing”和“Remeshing”。C区域为外流场区域,流场的尺寸为20b×26b。流场设置的较大,可以避免流场边界与水翼附近流场相互干涉而影响计算的准确性。

图3 流场网格

图4 水翼前、后缘网格
3 水翼颤振导数求解
Scanlan颤振导数理论内容较多,具体可参考文献[10],本文仅对关键点进行介绍。
对于均匀水平来流中攻角为0°的理想薄平板作频率为ω微小简谐运动时,薄平板的微幅振动会对平板上下表面的气流产生扰动。气流的运动反过来也会对平板产生作用力。由于平板自身运动所产生的的力称为自激力,自激力的理论解可表达为:

(1)
(2)
式(1)—(2)中:L、M分别为平板所受到的升力及扭矩;ρ为标准温度下流体密度;b为薄平板半宽,2b=板宽B;U为流体流速;h;α为平板的竖向位移和扭转角;K为无量纲折算频率,K=ωB/U,ω为振动圆频率。
式(1)—(2)是基于薄平板推导得出,Scanlan认为无论是钝体还是流线体都满足该式,并对式(1)—(2)进行了改编,引入一组仅与截面形状有关的无量纲参数“颤振导数”,以实现模型力和原型力的转换,此时自激力公式可改写为:
(3)
(4)
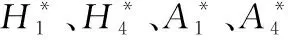
根据所求得的水动力数据,采用最小二乘法即可求解颤振导数,最终求得水翼的颤振导数值如表1所示。

表1 颤振导数值Table 1 Flutter derivatives
4 水翼临界颤振状态求解
求解颤振导数的目的是预测水翼的临界颤振状态,本文使用Scanlan于1951年提出的计算二维截面临界颤振速度的方法[10]。
(5)
将Scanlan自激力式(3)和式(4)代入2个自由度截面运动方程(5),并引入无量纲时间概念:s=tU/B,对截面运动方程进行无量纲化,可得:
(6)
(7)
定义未知函数X=ω/ωh,代入上述方程进行整理可得一个关于X的4次多项式。假定在颤振状态下X总为实数,可以得到实部和虚部2个方程为:
A4RX4+A3RX3+A2RX2+A1RX+A0R=0
A3lX3+A2lX2+A1lX+A0l=0
(8)
式(8)中各项系数值为:
(9)
式(8)为一元高次方程,可对其进行分别求解,实部方程和虚部方程分别可求得4个解和3个解。舍去负解和不合理的解,绘出实部解XR和虚部解Xi随折算速度Vr变化的曲线,它们的交点(XC,VrC)即代表临界颤振状态,临界颤振速度计算式为:
UC=BωhXCVrC
(10)
对于水翼算例,由求得的颤振导数,结合式(9)可以求得式(8)的各项系数,如在折算速度为3.33时,实、虚部方程为:
1.118 6X4-0.002 7X3-1.637 8X2+0X+0.456 4=0
-0.393 0X3-0.018 4X2+0.205 3X+0.011 3=0
利用高斯消元法对上式进行求解:实部方程解为:-1.042 1;-0.612 5;1.045 7;0.611 3。虚部方程解为:0.728 3;-0.720 3 -0.055 1,其他折算速度下求解同理。实、虚部方程的解舍去负解并进行二次多项式拟合,实、虚部解拟合曲线如图5所示。

图5 实、虚部解拟合曲线
拟合曲线的交点为(12.72,0.38),由式(10)求得临界颤振速度为:
Uc=BωhXCXrC=0.35×4.37×12.72×0.38=7.39 m/s
即求得该水翼的临界颤振速度为7.39 m/s。
5 验证与分析
使用纽马克-β法对第4节求得的结果进行验证。纽马克-β法是求解非线性振动的一种方法,本文根据其原理,编写UDF嵌入Fluent软件中实现水翼的流固耦合计算。判断水翼是否发生颤振的依据如图6所示。
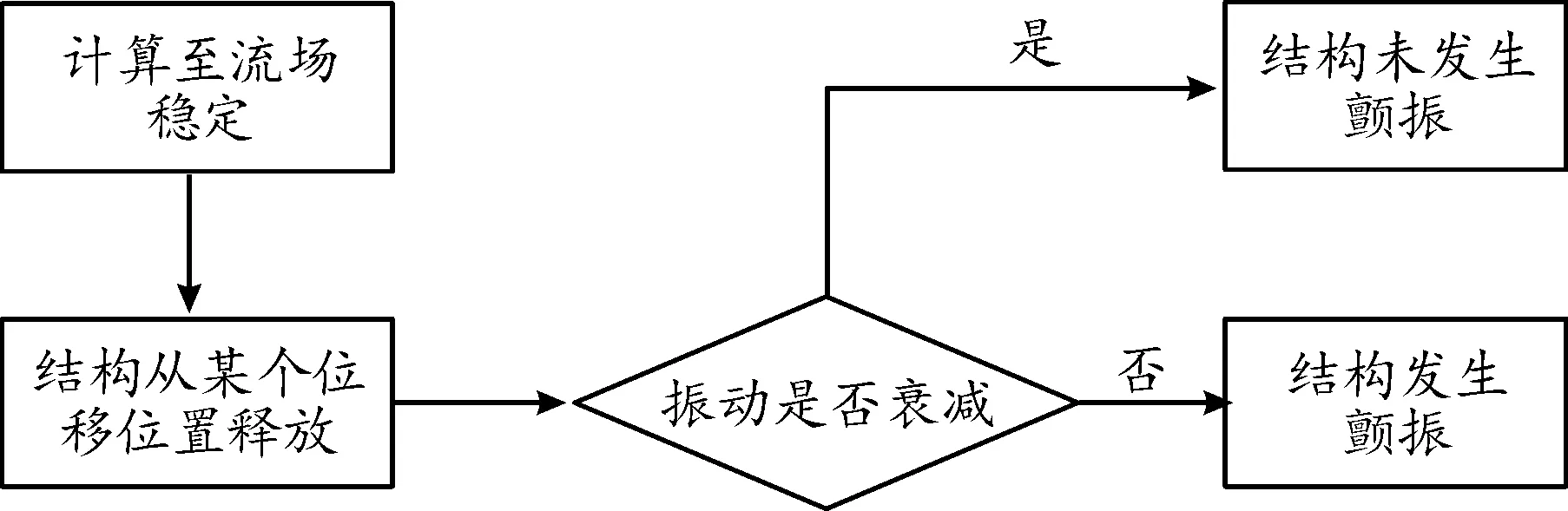
图6 临界颤振状态判断依据
给予水翼一个很小的位移,使水翼处于不平衡状态,待流场稳定后释放,水翼若在自激力的作用下,发生振幅越来越大的振动,则水翼进入颤振状态。编写Profile文件使水翼在前一秒内两自由度皆做频率为0.75 Hz的小幅正弦运动,待1 s时,竖弯和扭转2个自由度的振幅皆达到最值时,将处于不平衡状态的水翼释放,启动纽马克-β算法进行计算。
图7—图11给出了水翼在各流速下的竖向振动及扭转角时程图。

图7 扭转、竖弯振动时程图(U=3.0 m/s)

图8 扭转、竖弯振动时程图(U=7.0 m/s)

图9 扭转、竖弯振动时程图(U=7.3 m/s)

图11 扭转、竖弯振动时程图(U=8.0 m/s)
由图7—图11可知,前1 s内水翼竖弯及扭转方向皆由Profile驱动做规律的正弦运动。在流速为3 m/s时,水翼的振幅迅速衰减,而后做微幅振动以抵消流场输入的能量。当流速提升至7 m/s时,水翼被释放瞬间竖弯及扭转方向振幅明显要比U=3 m/s要大,振幅衰减速度比U=3 m/s时要慢。流速为7.3 m/s时,水翼竖弯及扭转方向皆做等幅简谐振动。当流速提升至7.5 m/s,2自由度方向的振动总体呈现缓慢发散态势。U=8 m/s时,发散速度要比U=7.5 m/s时快的多,结构已经发生颤振,在计算中由于振幅发散过快,水翼运动至动网格区域边缘导致计算报错。根据以上运动图像及分析可以推断,水翼的临界颤振速度约为7.3 m/s。
图12—图14给出了水翼在流速为7、7.3以及7.5 m/s时的升力、力矩时程图。
由图12—图14可知,水翼所受升力在1 s后的幅值差距不大,约为3 800 N左右,但之后流速为7 m/s时的水翼受到的升力越来越小,7.5 m/s时的水翼受到了越来越大的升力。流速为7.3 m/s时水翼受到了呈稳定大小以正弦规律变化的升力。水翼所受力矩规律与之相似。可见当结构进入颤振状态时,受到的升力及力矩会随时间推移而越来越大,相应的振动振幅也会越来越大,最终导致结构失稳。
图15—图17给出了水翼在流速为7、7.3以及7.5 m/s时的扭转、竖弯振动相轨线图。

图12 升力及力矩时程图(U=7.0 m/s)
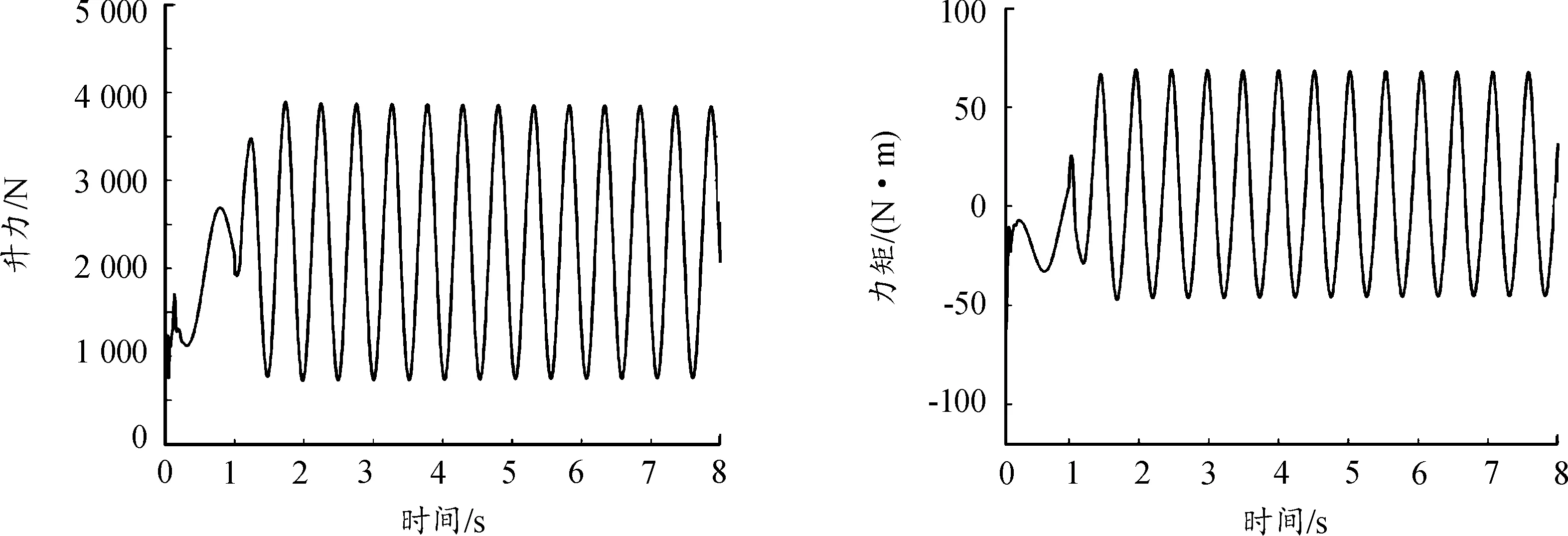
图13 升力及力矩时程图(U=7.3 m/s)

图14 升力及力矩时程图(U=7.5 m/s)
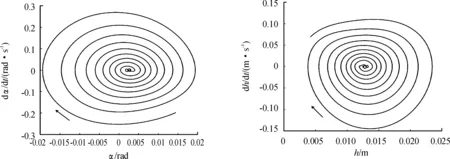
图15 扭转、竖弯振动相轨线图(U=7.0 m/s)
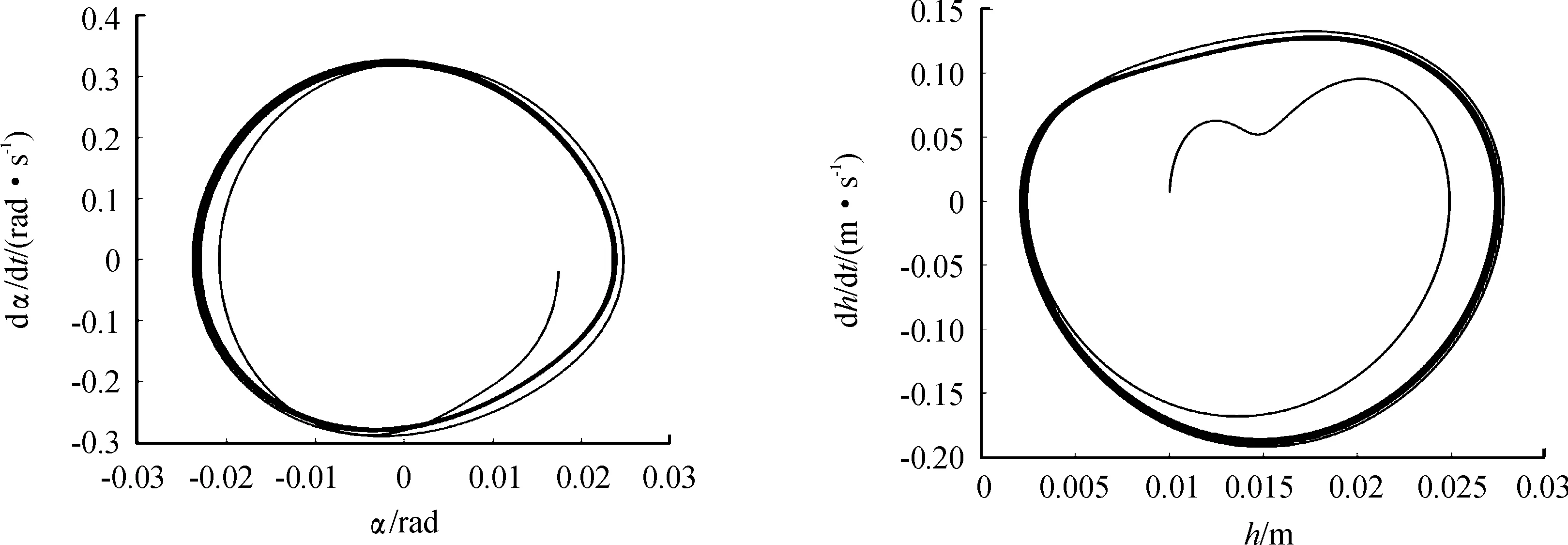
图16 扭转、竖弯振动相轨线图(U=7.3 m/s)

图17 扭转、竖弯振动相轨线图(U=7.5 m/s)
由图15—图17可知,在U=7.0 m/s时,水翼没有达到临界颤振速度,水翼的动能及势能在运动过程中逐渐被消散,水翼在竖弯及扭转自由度上的振幅及振动速度都在不断减小,相轨线不断向系统平衡点接近,直至达到稳定状态。当U=7.3 m/s时,竖弯及扭转振动演化为典型的极限环振动,水翼的能量在动能和势能之间不断转化。当流速提升至7.5 m/s时,水翼已达到颤振速度,系统的振幅及振动速度在流场不断做正功的原因下不断增大,直至结构破坏。
对水翼在2个自由度上的振动频率进行了统计,如图18所示。

图18 扭转、竖弯振动频率
由图18可知,2自由度的振动频率都随着流速的增加而逐渐减小。流速较低时,2自由度的振动频率差距较大,随着流速增加,振动频率趋向一致;当流速大于或等于临界颤振速度时,2自由度的振动频率相等。印证了颤振是由具有2个自由度以上的结构物以同一频率耦合振动的现象。
经过以上分析,由纽马克-β法求得的水翼临界颤振速度为7.3 m/s,与Scanlan颤振导数理论求得的结果基本一致。
6 结论
1)引入Scanlan颤振导数理论,由该理论成功求解水翼的临界颤振速度并进行了验证,证明Scanlan颤振导数理论可以应用在水翼的临界颤振状态求解。
2) 由纽马克-β法对水翼的振动状态进行了分析,水翼一旦进入颤振状态,振幅会不断扩大直至破坏。升力和力矩的变化情况和振幅一致。
3) 水翼进入临界颤振状态时,动能和势能总和不变,并在不断转化中。2自由度的频率一致,印证了颤振是由具有2个自由度以上的结构物以同一频率耦合振动的现象。

