基于剖分网格的电磁环境可视化

胡豪杰,方胜良

(航天工程大学， 北京 101400)

1 引言

信息化战场分秒必争，如何高效呈现战场电磁环境的各维度信息，提供高效、直观的电磁环境可视化视图成为提升对电磁态势控制能力的关键[1]。

关于电磁环境的可视化展示，相关论文以可视化雷达作用区域、探测范围或者以热力图形式对电磁态势进行显示为主。如文献[2]讨论了山地、建筑物遮挡下的雷达辐射范围变化情况，通过判断两点之间能否通视来绘制雷达辐射范围的三维图像，但其仅对辐射范围进行了可视化，并未呈现电磁场内部细节信息。文献[3]立足于战场电磁态势可视化，以装备电磁辐射范围为重点，构建了通信、侦察以及干扰情况下的雷达作用范围可视化视图。关于空间电磁场绘制方法，以面绘制和体绘制2种方法为主。文献[4]研究了柱坐标系下电磁场数据的可视化问题，对面绘制算法Marching Cubes进行了改进，利用柱坐标系下规则网格数据进行等值面提取，改进体绘制光线投射算法，使其能够适应柱坐标系下的电磁场数据绘制。文献[5]将等值面绘制与体绘制方法进行融合处理对电磁环境进行可视化，设置了多层等值面用以表示不同阈值电磁场的分布，并用体绘制增强数据的表现能力。文献[6]采用了面绘制算法对气象雷达边缘轮廓的进行了三维重构，并对比了Delaunay三角网、Crust以及Marching Cubes几种曲面重构算法的优劣，验证了Marching Cubes算法的独特优势。

综上所述，目前电磁环境三维可视化的研究中，大多数文献通过绘制雷达探测范围覆盖曲面来表示雷达的作用距离，或者采用热力图形式对电磁场进行可视化显示，难以表示电磁场内部细节特征对于整体电磁态势的影响。在可视化绘制方法上，以面绘制方法为主对数据进行快速可视化重构。面绘制通过对三维模型表面进行轮廓识别、分割、提取、映射等步骤，实现对三维数据场或物体表面特征的绘制，相比较于体绘制方法，面绘制仅能够提取三维模型表面信息，难以展示电磁场内部细节特征与外部表象之间的关系，但是，其原理简单、快速绘制等优点也使得面绘制方法成为三维模型表面纹理绘制的主要方法之一[7]。为此，引入剖分网格对电磁场数据进行组织，便于数据的查询检索操作并将面绘制Marching Cubes算法与剖分网格相结合，减少了算法对大量处于非等值面的空数据立方体的遍历查询，从而提升面绘制的效率，同时通过改变可视化策略对三维空间范围内经纬高3个维度的剖分实现对电磁场内部细节特征的可视化，满足了用户对电磁场整体分布和细节特征的多视角观察需求。

2 空间电磁场数据剖分理论

2.1 GeoSOT-3D空间剖分理论

GeoSOT-3D剖分网格是由北京大学程承旗教授团队提出的一种整分、整秒、整型剖分方法，全称为基于2n整型一维数据全球经纬度剖分网格(Geographical coordinate global Subdivision based on One-dimension-integer and Two ton-th power,GeoSOT)，按照八叉树划分的方式构建了覆盖全球范围的0-32级网格，支持多粒度的划分，网格最大尺度为全球(0级网格)，最小尺度约为1.5 cm(32级网格)[8-9]。

GeoSOT-3D剖分网格通过对经纬度的3次扩展，即将地球表面经纬空间由180°×360°扩展至512°×512°，将1°由60′扩展至64′，将1′由60″扩展至64″，与高程信息结合，实现了对经纬高3个维度共计512°×512°×512°的八叉树整度、整分、整秒剖分，由于经纬度扩展空间的存在，不属于实际地理空间的扩展范围不再进行剖分处理[10]，此外由于南北两极地区上空网格所占空间逐渐变小，剖分网格在两极地区的剖分方式做了部分调整，在此不做详细解释。

在完成GeoSOT-3D格网剖分以后，按照“Z”序为每个体块赋予唯一层次性编码，将体块的编码作为数据存储、索引和运算的基本，形成“体块对应编码-空间剖分体块-空间数据信息”的对应关系。

由于网格采取八叉树方式向下剖分，因此在编码时按照“Z”序对每个剖分体块进行编码，其中将北半球中国所在区域定义为G0，然后按照“Z”序对剖分体块进行填充，在完成第二级剖分以后，按照三维“Z”序由0～7进行编码，以次类推，完成对本级剖分体块的编码。由于编码的唯一确定性，通过编码即可查询出该体块所在地理空间位置。

2.2 基于剖分网格的空间电磁场数据组织模型

GeoSOT-3D剖分网格构建了全球范围内的三维空间立体剖分，利用剖分网格建立空间电磁场数据的组织模型，可以实现对电磁场数据的多粒度表达、全球统一编码、快速查询与检索的统一。模型的可视化表达架构如图1所示。

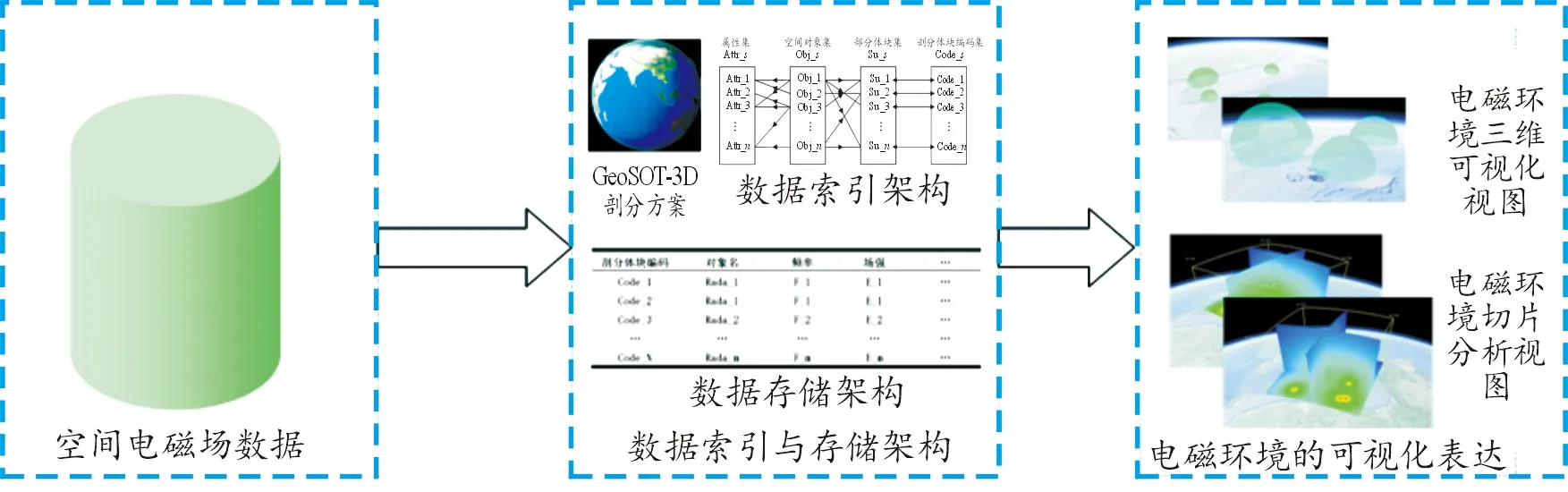
图1 基于剖分网格的电磁环境可视化表达架构

2.2.1空间电磁场数据组织模型建立

根据空间电磁场数据的采样粒度选择对应的剖分网格层级建立基于剖分网格的电磁场数据组织模型，形成“空间电磁信息-空间剖分体块-体块对应编码”特征结构。本文中设计了空间电磁场数据组织模型及多层级数据转换策略，通过对初始剖分网格层级下数据的采样获取全层级下的数据组织模型，避免了对空间电磁场数据的重复采样与数据组织。

模型建立流程如下：

Step1确定空间电磁场数据的采样粒度δ；

电磁场在空间的分布具有连续性，由于数据采集手段的限制，无法对空间数据进行连续采样，因此，在数据模型建立前，要确定空间电磁场数据的采样粒度。

对于获取的空间电磁场数据，假设数据在经纬高3个维度的间距分布为：经度间距为Δlon，纬度间距为Δlat，高度间距为Δh，则其采用粒度为三者最小值，即：

δ=min(Δlon,Δlat,Δh)

(1)

Step2根据采样粒度确定GeoSOT-3D网格剖分层级；

剖分层级越高，剖分体块的几何体积越小，随之则数据量越大，因此剖分层级的确定应当尽量接近采样粒度，以保证采样得到的数据点能够被最大限度利用，且建模后数据量保持基本不变。在确定空间电磁场数据的采样粒度δ后，按照如下原则确定GeoSOT-3D剖分网格层级N：

规则1如果size(n)=δ,则N=n;

规则2如果size(n+1)≤δ≤size(n),则N=n+1;

其中，表示第n层级下的剖分粒度。

Step3建立空间电磁场数据与N级剖分网格编码下的映射关系；

根据空间电磁场数据采样的经纬高，计算其对应的剖分网格，具体计算对应关系如下：

假设数据采样点P坐标为集合(lonp,latp,hp),网格层级N，该层级下网格体块大小为(Δlon,Δlat,Δh)，其中某一体块所占据空间坐标范围为集合(lonmin,lonmax)，(latmin,latmax)，(hmin,hmax)，则根据映射法则，当采样点经纬高坐标落入体块坐标范围时，即满足如下规则，将采样点属性映射至网格坐标。

lonmin≤lonp≤lonmax

latmin≤latp≤latmax

hmin≤hp≤hmax

(2)

Step4空间插值；

空间电磁场数据分布的不均匀性以及采样的不完全性，因此，将空间电磁场数据映射至剖分网格过程中，可能存在部分剖分体块缺失属性信息。此时，需要根据已知剖分体块的属性及数值拟合出未知剖分体块的属性及数值，采用空间插值的方法对数据进行处理，补全缺失的属性信息。

Step5建立剖分层级N下的频谱测绘数据组织模型；

由于GeoSOT-3D网格剖分具有全球唯一性，因此，在建立频谱测绘数据与剖分网格的对应关系后，采用GeoSOT-3D网格编码方案对每个体块进行编码，得到基于GeoSOT-3D网格剖分的频谱测绘数据组织模型。

2.2.2数据存储

网格编码对于空间实体数据以及空间场数据的组织形式略有不同，对于实体数据根据实体数据占据的网格体块进行映射，空间场数据需要界定空间场所体块层级、体块区域等，然后以体块为桥梁建立体块编码与场数据属性间的关联，我们只讨论空间电磁场数据的存储与索引问题。

对于空间电磁场数据，由于同一电磁场数据可能会对应多个剖分体块，并且每个剖分体块的属性不尽相同，因此空间电磁场数据的存储结构如表1所示。

表1 空间电磁场数据存储结构Table 1 Storage structure of electromagnetic data

某一对象可能对应多个剖分体块，对于某一剖分体块，也可能对应多条属性。因某一定层级表达粒度下，编码位数相同，也可使用数组结构存储剖分体块编码，减少数据冗余。

2.2.3数据索引

剖分体块与剖分体块编码之间是一一对应的关系，空间对象与剖分体块之间是一对多的关系，空间对象与属性数据集之间也是一对多的关系。由此构成“剖分体块——体块编码——属性数据集”的数据结构模型。

按照剖分编码设计，数据的查询检索可以有如下几种方式[11]：

一对多的查询方式：根据属性查询空间对象和其所在位置；根据空间对象查询其属性和位置；根据空间位置查询该空间位置处的空间对象和属性。

多对一的查询方式：根据空间对象和其所在位置查询其属性；根据属性和位置查询空间对象；根据空间对象和属性查询其所在位置。数据的查询检索模型如图2所示。

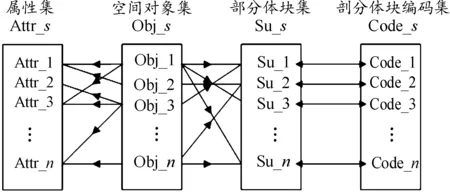
图2 数据的查询检索模型

2.3 运算原则

在剖分网格模型下，空间电磁场数据是以剖分体块集合的形式进行组织的，并由剖分体块编码及其属性定义，因此，对数据的运算转变为对集合的运算。主要包含体块基础运算、体块集合运算以及典型空间分析等。因篇幅有限，只对与面绘制相关的几个运算规则进行说明。

2.3.1相交运算

通过相交运算计算多部雷达空间覆盖范围的交界，以2部雷达交界为例，数学表达模型如下：

在剖分层级L下，对于场强值为EdBm的雷达A和雷达B雷达包络体块集合分别为集合{CodeA}和集合{CodeB},通过相交运算来求解2个雷达包络的交界，记为S={CodeA}∩{CodeB}。

2.3.2位移运算

通过位移运算实现对剖分体块及其属性信息的快速查询，以体块CodeM为例，查询距离其经纬高分别为Δlon,Δlat,Δh上的体块CodeN，其数学表达模型如下：CodeN=Move(CodeM,VM)。

其中，VM=(Δlon,Δlat,Δh)。

2.3.3聚合和解聚

剖分体块聚合和解聚的过程就是空间电磁场数据在不同剖分层级间相互转换的过程，分为由小体块到大体块的聚合以及由大体快到小体块的解聚。空间电磁场数据剖分模型将处于空间范围内的电磁场按照指定层级进行剖分，从而形成该层级下的空间数据集合，每个剖分体块的空间位置和携带的空间电磁场属性信息由剖分体块的编码和空间电磁场编码唯一确定，即

(3)

式中：E表示空间电磁场；Codei表示代表剖分层级下体块的编码；CodeE表示对应的空间电磁场属性编码信息。

聚合：当空间电磁场占据区域较大或者选择的剖分层级较高时，则剖分体块的数目N会急剧增大，为便于数据组织、减少存储空间、满足电磁环境多尺度表达需求，可以将处于较高剖分层级的体块进行聚合来降低数据规模从而提升数据的组织管理能力。此时，空间电磁场E表达如下：

(4)

式中：Codei, j表示剖分层级i下第j个体块的编码；CodeE表示对应的空间电磁场属性编码信息；M表示最大的剖分层级。

对于空间电磁场信息，其聚合的原则是遍历空间电磁场的编码集，同属一个父体块的编码用父体块编码代替，直至对空间范围内所有体块完成聚合。

解聚：解聚的过程与聚合相反，将父体块的分解成子体块来显示更加精细的电磁环境相关属性信息，解聚的原则是确定需要解聚的体块集合以及目标子体块层级，然后将集合中的父体块进行剖分得到目标层级的子体块，在剖分过程中，子体块的属性编码通过对应父体块属性编码的线性插值完成。

3 基于剖分网格的面绘制算法

面绘制主要有Marching Cubes算法、MarchingTetrahedra算法以及Dividing Cubes 算法。几种算法原理相似，其中Marching Cubes算法通过将三维模型分割为六面体的方式进行等值面查找，对于某些特定数据集采用MarchingTetrahedra算法进行分割，四面体的数据组织方式有利于等值面的查找，Dividing Cubes 算法则针对数据密度较大的数据集进行绘制[12-13]。本文中数据采用基于GeoSOT-3D剖分网格的数据组织模型，GeoSOT-3D剖分网格按照八叉树剖分的方式构建覆盖全球范围的数据立方体，综合考虑，采用同样利用具有严密网格组织逻辑的Marching Cubes算法(简称MC算法)绘制电磁态势的表面纹理。

3.1 Marching Cubes算法

MC算法最初是由Lorensen于1987年提出，也称为等值面提取算法，是一种通过提取等值面来重构数据三维形态的算法[14]。MC算法将三维体数据存放于六面体的顶角上，其基本原理就是通过遍历数据立方体中的数据单元，寻找出与等值面相交的立方体集合，判断六面体顶点与等值面的关系，然后通过插值算法构建出三维数据体的轮廓。算法的基本流程如图3所示。

图3 MC算法流程框图

根据等值面属性设定阈值，然后判断数据立方体8个顶点与阈值的大小关系，大于阈值的顶点记为“1”即标记点，小于阈值的顶点记为“0”即非标记点，8个顶点遍历完毕后可以创建八位的标识码。由于数据的连续性，等值面必位于标记点与非标记点之间，因此可以根据标记点与非标记点的位置关系提取出该数据立方体内部的等值面。

MC算法的核心在于寻找与等值面相交的数据立方体并判断该立方体顶点与等值面的相对位置关系，由于立方体的8个顶点必处于“0”或者“1”状态，因此根据MC算法立方体顶点与等值面的关系分布共有28～256种情况。在实际过程中，将所有的等值面分布情况构建成查找表，然后遍历所有的数据立方体，并记录下数据立方体的等值面分布情况与查找表对比，将所有处于等值面上的数据立方体按照等值面相连即可重构出数据的三维轮廓。为简化计算，根据立方体的对称性和旋转性可以将该256种情况简化为以下15种，如图4所示。

图4 等值面与数据立方体顶点关系图

3.2 剖分网格下的算法优化

通过等值面提取的基本原理可以看出，MC算法由于需要遍历三维空间数据体内每个数据立方体的8个顶点，而数据的等值面是一个曲面，横跨等值面的数据立方体占所有立方体的比例很低，导致大部分时间浪费在处理处于非等值面上的数据立方体上。相关研究表明，MC算法超过一半的时间用于遍历空的数据立方体[8]，严重降低了等值面的绘制效率。

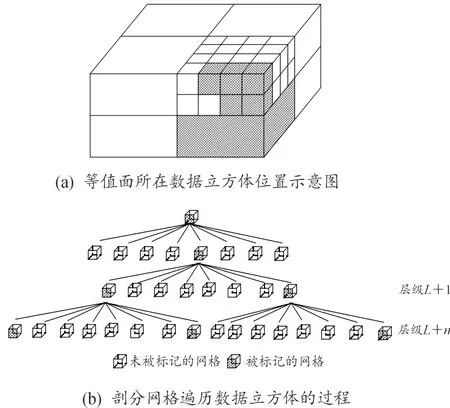
图5 基于GeoSOT-3D网格的MC算法原理示意图

由于剖分网格在空间上采用八叉树剖分的方式，可以利用此特性优化等值面查找过程。如图5所示，显示了GeoSOT-3D剖分网格下等值面的查找过程。首先对较低层级的剖分网格进行遍历，对其顶点进行标记，若全为“0”，则停止对该网格及其剖分层级网格的查找；若存在标记为“1”的顶点，则将该网格进行剖分继续查找等值面。然后以此类推，直至所需精度下剖分网格体块，最终得到等值面所在剖分网格的精确位置。

具体算法流程如图6所示。

图6 基于GeoSOT-3D网格的MC算法搜索标记流程

4 实验与分析

4.1 仿真环境

为验证本文方法，构建了基于剖分网格的频谱态势可视化原型系统，实现了相关功能，仿真具体软硬件配置如表2、表3所示。

表2 实验硬件环境Table 2 Hardware environment

表3 实验软件环境Table 3 Software environment

仿真实验数据为经度108°～118°，纬度16°～22°，高度0～1 000 km，按照自由空间传播模型进行计算得到该三维区域内场强密度值，随机布置5个辐射源，均采用全向天线，具体设置参数如表4所示。

表4 辐射源参数设置Table 4 Radiation source parameter setting

4.2 结果分析

为验证本文中所提方法的有效性，设计了三维重建视觉效果对比实验用以说明本文方法在视觉上能够还原绘制出电磁环境三维轮廓，并通过算法性能的实验数据的详细对比验证了本文方法相比较于传统MC算法的效率提升。

4.2.1三维重建视觉效果对比

图7给出了传统MC算法和本文改进MC算法的三维重建效果对比图。实验采用剖分网格层级为12层级，对应数据立方体约为16 km×16 km×16 km，场强等值面取值38 dbm。从视觉效果看，2种方法均能够绘制出电磁场的表面轮廓，本文改进算法继承了传统MC算法在表面轮廓绘制的优点，能够绘制出电磁环境的三维轮廓，且重构视觉效果符合空间电磁场分布情况。

图7 重构图视觉对比

4.2.2算法性能对比

为对比传统MC算法与本文改进算法性能的优劣，采用三角面片数、遍历数据立方体数目、总体绘制时间四个指标进行对比，其中三角面片数的多少与三维重建的效果有关，面片数越多则表面轮廓越光滑，其余两个指标与重建的效率有关，遍历的数据立方体数目和总体绘制的时间越少则算法的效率越高。算法性能对比表如表5所示。

表5 算法性能对比表Table 5 Algorithm performance comparison table

通过对比可以得出：

1) 本文中改进算法与传统MC算法在绘制三角面片数目上基本一致，两者的三维重建视觉效果对比也佐证了该结论。

2) 在绘制效率上，本文改进算法在遍历数据立方体数目上比传统算法减少约76%，总体绘制时间减少约34%，这是由于层级L与层级L+n下网格体块数目差为8n，通过这种低层级确定横跨等值面网格所在区域、高层级确定横跨等值面网格精确位置，可以有效减少对空数据立方体的查找，从而提升算法效率。具体效率提升与采用的剖分网格层级以及等值面分布有关。

为验证本文算法在不同剖分网格层级下三维重建能力，图8给出了不同网格层级下的绘制结果对比图。图9给出了不同网格层级下绘制等值面的时间开销，通过对比可以看出，层级越小其绘制效率高但是表面轮廓相对粗糙，这是由于绘制精度与立方体网格大小有关，精度越高需要遍历的网格立方体越多时间开销也就越大。

图8 不同等级网格绘制结果对比

图9 不同网格层级下绘制等值面的时间开销

4.2.3电磁环境三维剖分可视化表达

为了增强可视化系统的对于电磁环境内部细节特征的表现能力，从高度和经纬3个维度对仿真区域内电磁场切面进行可视化，通过改变经纬高的显示策略可以查看任意高度、长宽切面上的磁场分布情况。图10给出了仿真实验条件下的电磁态势空间切面分布情况，通过交互操作实现对不同高度和经纬度频谱态势切面的可视化查询，允许用户交互控制的参数包含：剖分层级、经纬、维度、高度和等值面阈值，从而满足用户多视角的观察需求。

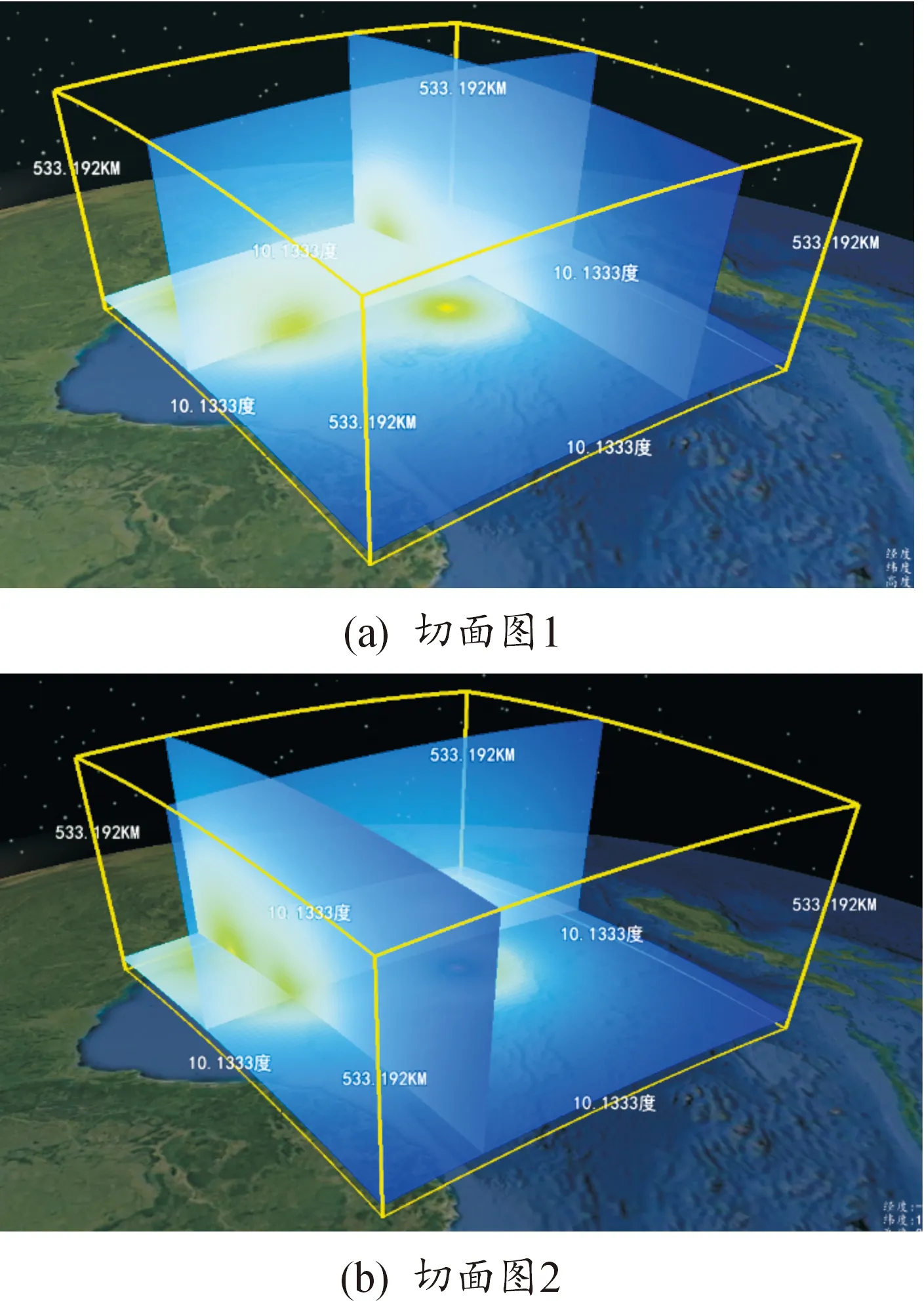
图10 三维切面图

5 结论

本文中建立了基于剖分网格的电磁数据组织模型有效避免了对空间电磁场的重复采样，改进了面绘制MC算法有效提升了绘制效率，采用三维剖分表达的方法实现了对电磁场内部细节特征的可视化。仿真实验显示，本文方法能够精确绘制出电磁场的空间轮廓，验证了本文方法在可视化效果上的有效性；在相同空间采样粒度的前提下，相比较经典算法本文方法能够有效提升绘制效率30%左右，且可以通过改变剖分网格层级实现对空间电磁场的快速绘制；通过三维剖分表达实现了对空间经纬高3个维度上电磁场细节特征可视化表达。通过本文中工作可以实现对空间电磁场的数据组织与可视化，帮助用频人员快速掌握电磁环境、做出科学决策。

本文中尚存在以下2点可后续改善：① 考虑与地形结合的电磁场三维可视化，通过对地形编码集合与电磁场空间范围编码集合的求交运算，计算地形对于电磁场传播的影响；② 考虑多种电磁传播影响因子对于可视化结果的影响，将大气损耗因子转换为损失函数与剖分网格相结合进行运算，对多种传播影响因子下电磁场空间分布进行可视化。