水下爆炸载荷下舰船双层底部结构的毁伤特性
陈岩武, 孙远翔, 王成
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
0 引言
舰船在服役期间极易遭到鱼雷、水雷等水下兵器爆炸载荷的威胁[1-3],为增强防护能力,现代水面舰船底部多为双层结构。然而水下爆炸载荷在双层结构中的传递过程与双层底结构的响应特征均比较复杂[4-5],张振华等[6]试验研究了远场爆炸冲击波在双层底部结构间的传播规律。Liu 等[7]使用改进的 2 阶双重渐进近似方法,研究了冲击波载荷在充水双层壳体结构间的传播机理。古滨等[8]建立了水下爆炸载荷与双层壳结构的耦合计算模型,探究了不同板间介质对冲击波载荷传播的影响规律。郭君等[9]采用AUTODYN 研究了爆炸冲击波载荷在双层底结构中的传播,并分析了双层底结构的破坏过程。
上述研究仅涉及远场爆炸冲击波载荷在双层结构中的传播特性,未对气泡载荷进行研究。当舰船双层底部结构遭遇水下战斗部近距离爆炸载荷时,爆炸冲击波使外板出现破口,紧接着,爆炸气泡会通过外板破口进入舰船底部双层板间舱室,进而对内底板造成毁伤[10]。Quah 等[11]使用电火花气泡代替爆炸气泡,研究了双层板间距与气泡射流形成方向的关系。Zeng 等[12]发现了双层板间的三种气泡射流形式。Su 等[13]进行水下微当量炸药爆炸实验,捕捉到了气泡坍塌和射流形成的细节。 Chen 等[14]进一步研究了爆距、破口大小、双层板间距对气泡射流载荷的影响。盛振新等[15]建立了爆轰产物冲击双层板结构的内板载荷理论模型,并分析了药量、破口半径和舱室宽度对气泡运动和内板壁压的影响规律。
但上述研究[11-15]均将内外板视为刚性结构,忽视了板的变形和破坏过程与气泡脉动过程的耦合作用,难以真实反映舰船在水下爆炸载荷下的响应特征。张梁[16]考虑结构的弹塑性响应,使用 LSDYNA 模拟了爆炸气泡在双层带破口空舱附近的运动特性以及舱室内压特性。吴林杰等[17]实验研究了水下接触爆炸冲击波与气泡载荷联合作用下防雷舷侧双层空舱的动态响应。杨棣等[18]根据冲击因子设定水下爆炸工况,总结了近场及接触爆炸载荷下双层底结构的损伤模式。陈娟等[19]研究了水下近场爆炸载荷下,双层底结构的整体与局部毁伤情况。苏标等[20]通过高速摄像机拍摄水下光学影像,探究了不同爆距下板架的损伤模式,但由于受到实验手段的限制,并未捕捉到气泡与双层板架结构的详细相互作用过程。
总之,目前关于双层板结构的内板受到的爆炸气泡载荷研究较多,关于爆炸气泡与双层板结构的相互作用过程研究较少。鉴于此,本文首先进行电火花气泡与带破口双层结构相互作用实验,并使用LS-DYNA 对实验工况进行建模,验证数值模型的有效性。然后建立实尺度舰船双层底舱段数值模型,对水下爆炸载荷下舰船内、外板的变形和破坏过程与气泡脉动的耦合作用进行模拟,获得气泡与双层板结构的详细相互作用过程,探究不同爆距、不同双层板间水位条件下舰船双层底结构的毁伤特性。
1 电火花气泡实验
1.1 实验装置与实验模型
为清晰地观测到气泡与双层底板的相互作用,本文使用电火花气泡代替爆炸气泡,进行电火花气泡与带预制破口的双层底结构相互作用实验。使用的电火花气泡发生装置包括充放电开关、电容器、铜丝、高速摄像机同步触发接口及遥控器等。根据电容器充电电压的不同,该装置可产生直径30~ 50 mm 的电火花气泡。
设计的带预制圆形破口的双层底结构实验模型如图1 所示,由内底板、外底板、支撑结构和板间水组成,在外底板正中心预制一个圆形破口。模型中支撑结构高度l=25 mm,板间水位h=15 mm,预制圆形破口直径d=20 mm,电火花气泡在破口正下方R=10 mm 处生成。

图1 带预制破口的双层底结构实验模型示意图Fig. 1 Schematic of experimental model of doublebottom structure with a prefabricated hole
实验模型的内板和外板均为1 mm 厚的铝合金板,四周支撑结构为透明亚克力板,以保证高速摄像机能够清晰捕捉到板间的气泡脉动画面。事先使用油纸对外板破口进行密封,这样即能保证电火花气泡生成瞬间产生的冲击波可轻易冲开油纸(类似于实际海战中冲击波对外板造成的局部毁伤),又能使冲击波到达模型之前保证内板底板之间的密封性,实现预定的双层板间水位。
1.2 实验过程
实验开始时,首先将实验模型放置于尺寸为500 mm×500 mm×1 000 mm 的透明水槽中,并将电极两端的铜丝进行搭接,使铜丝的交点位于实验模型正下方10 mm 处。使用日本Photron 公司生产的SA4 高速摄像机,将高速摄像机对准铜丝交点处,并将拍摄帧率调节为8 000 帧/s,曝光时间为10 ms,同时连接高速摄像机与电火花气泡实验装置,实现二者的同步触发,保证电火花气泡生成的同时,高速摄像机同时进行拍摄。随后打开充电开关,对电容器充电至600 V,充电完成后点击遥控器的放电开关,使电路发生短路,铜丝交点处被瞬间融化并使周围的水汽化,形成电火花气泡,气泡的球心处于铜丝的交 点处。
实验结束后,使用PFV4 软件对高速摄像机拍摄到的气泡脉动数据进行处理,得到电火花气泡的最大半径约为22.61 mm。
2 数值模型与有效性验证
2.1 数值模型
使用LS-DYNA 软件对1.1 节中的实验工况进行建模,由式(1)计算可知,在自由水面附近,0.002 6 g TNT 产生的爆炸气泡最大半径为22.48 mm,与电火花气泡最大半径十分接近,因此,选取该当量的TNT 作为爆源进行模拟。
式中:W为装药质量(kg);H为爆炸所处水深(m)。
由于电火花气泡威力较小,实验过程中内、外板均未出现明显的变形,可以将内、外板视为刚性结构,使用*MAT_RIGID 材料模型描述,使用铝合金的材料参数,密度ρ=2.81 g/cm3,弹性模量E=71 GPa,泊松比μ=0.33。水介质和空气均选用*MAT_NULL 材 料 模 型 和 *EOS_LINEAR_ POLYNOMIAL 多项式状态方程描述,如式(2) 所示:
式中:p为压力;Ci(i=0, … , 6)为常数;,ρ为冲击波压缩后材料的密度,ρ0为材料的初始密度;E为材料单位体积内能,其取值及单位如表1 所示。

表1 水和空气的材料模型及状态方程参数Table 1 Material models and equation of state parameters of water and air
炸药采用*MAT_HIGH_EXPLOSIVE_BURN材料模型和JWL 爆轰产物状态方程描述,如式(3)所示。炸药为球形装药,装药半径为0.725 mm。
式中:p为爆轰产物的压力;V为爆轰产物的相对体积;A、B、R1、R2和ω为表征炸药特性的参数。参数取值如表2 所示,其中DC-J和pC-J分别为炸药的爆速和爆压。
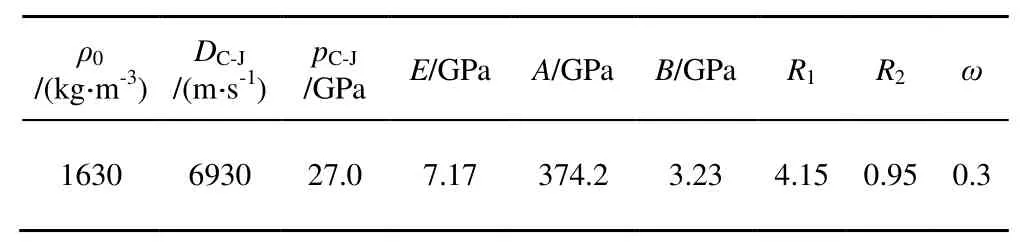
表2 炸药的材料模型及状态方程参数Table 2 Material model and equation of state parameters of the explosive
由于模型具有对称性,为减少计算时间,建立图2所示的1/4 有限元数值模型,水域尺寸为80 mm× 80 mm×90 mm,空气域尺寸为80 mm×80 mm×30 mm,在两个对称面上施加位移约束,实现对称边界条件,空气域的上表面和水域的下表面施加无反射边界条件,水域和空气域划分的网格尺寸均为0.5 mm。
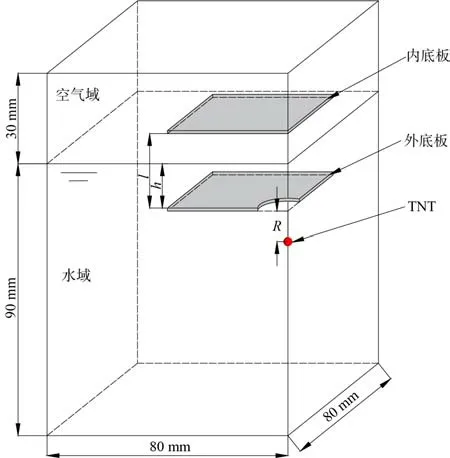
图2 有限元模型Fig. 2 Finite element model
其中内、外底板采用Lagrange 实体单元,水、空气和炸药采用ALE 实体单元,使用关键字*CONSTRANED_LAGRANGE_IN_SOLID 定 义Lagrange 实体单元与ALE 实体单元之间的流固耦合作用,采用允许Lagrange 实体出现侵蚀的罚函数耦合方式,并使Lagrange 实体单元与所有的多物质组耦合。使用*LOAD_BODY_Z 关键字定义整个模型的重力场,以模拟自由液面的水冢现象。
2.2 有效性验证
图3 和图4 所示分别为气泡脉动过程的实验结果与数值模拟结果。实验过程中,高速摄像机与电火花发生装置为同步触发,但电火花气泡的生成可能存在时间延迟,导致实验结果的时间较数值模拟结果存在0.175~0.200 ms 的延迟。

图3 不同时刻气泡形态(实验结果)Fig. 3 Bubble shape at different moments (experimental results)

图4 不同时刻气泡形态和流场压力云图(模拟结果)Fig. 4 Bubble shape and flow field pressure at different moments (simulation results)
气泡在带破口双层结构下方的脉动过程较为复杂。气泡在膨胀时穿过外板破口,进而被分割成了外气泡和内气泡,内气泡的膨胀导致板间液面处出现水冢,如图3(a)和图4(a)所示。紧接着,外气泡和内气泡同时达到最大,外气泡的半径达到 22.61 mm,而内气泡呈椭圆形,半长轴长度达到17.56 mm,此时液面水冢开始接触到内板。之后外气泡和内气泡均开始收缩,而液面水冢开始变高变窄,如图3(c)和图4(c)所示。之后,内气泡消失,在外板破口处出现压力达到2.5 atm 的高压区,使气泡形成向下的射流,高压区随着射流的形成由开始向下移动,如图3(e)和图4(e)所示,高压区逐渐转移到气泡底部。与此同时,液面水冢持续作用于内板,由于外气泡的收缩作用,液面不再保持水平,开始向下凹陷。最后气泡收缩到最小,产生压力高达10 atm 的二次压力波,对内、外板均产生严重的二次毁伤作用。由此可见,数值模拟得到的气泡动态演化过程与实验结果较为一致,验证了所建数值模型的有效性。
3 实尺寸舰船双层结构毁伤特性研究
为更加真实地反映海战情况,以实船尺寸舱段为研究对象,然而由于实船实验准备周期长、花费过高,因此使用数值模拟的方法进行研究。基于 第2节数值模型中选取的单元算法、流固耦合方式和材料参数,建立实尺寸舰船双层底舱段模型,探究舰船双层底板结构在水下爆炸载荷下的毁伤特性。
3.1 数值模型建立
建立图5 所示的真实舰船双层底舱段模型[21],舱段半宽620 cm,舱段长度600 cm,吃水深度415 cm,水面以上高度257 cm,舱段的双层底间距为100 cm。
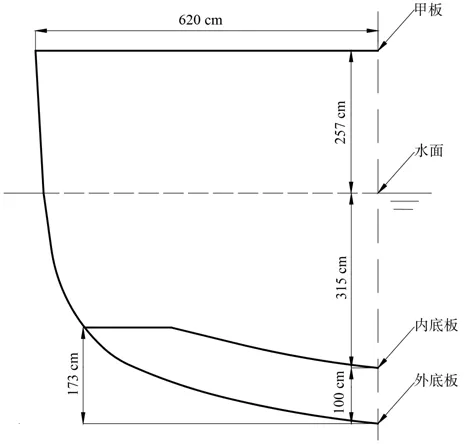
图5 舰船舱段模型截面尺寸图Fig. 5 Section dimension drawing of ship cabin model
整个舱段的板厚均为2 cm,材料为船用907A钢[22],使用塑性随动强化材料模型,如式(4)所示,使用*MAT_PLASTIC_KINEMATIC 关键字描述:
式中:σ0为初始屈服应力,取490.1 MPa;ε˙为应变率;C为应变率参数C=6 180 s-1;P=1.56。当材料的等效塑性应变大于失效应变0.25 时,材料发生失效。
钢板密度为 7.85×103kg/m3,弹性模量为 207 GPa,硬化模量为1.05 GPa,泊松比为0.3。选取 51 kg 球形 TNT 炸药作为爆源,装药半径R0=19.54 cm。由于舰船舱段模型具有对称性,为减少计算时间,建立 1/4 尺寸模型,水域尺寸 1 000 cm×1 000 cm×1 465 cm,空气域尺寸 1 000 cm×1 000 cm×385 cm。计算时长1 000 ms,大于气泡一次脉动周期。
3.2 数值模拟工况和结果
由于引信和制导的误差,水下战斗部会在舰船底部不同距离处发生爆炸,又由于压载和防护的需要,舰船双层底板间的水位会出现不同的装载状态。鉴于此,本文通过改变爆距R和双层板间 水位h,设置15 个数值模拟工况,如表3 所示。爆距R和双层板间水位h的定义如图6 所示,炸药位于舰船正下方。
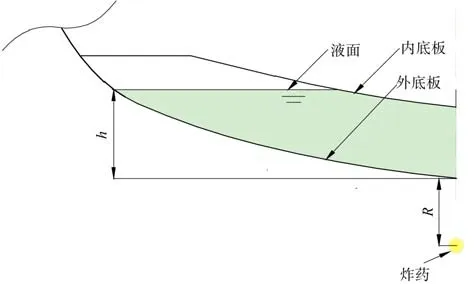
图6 爆距R和双层板间水位h定义示意图Fig. 6 Schematic of the definitions of explosion distance and water level between double bottoms

表3 数值模拟结果Table 3 Numerical simulation results
对数值模拟结果进行后处理发现,部分工况的外底板出现花瓣型破口,另一部分出现塑性大变形,而内底板均出现塑性大变形,为了便于对双层板结构的毁伤机特性进行合理分析,下面对板挠度、板破口尺寸和舱段位移进行定义。
图7 给出了舱段初始状态与毁伤后状态示意图,首先在舱段模型上取了3 个关键点,I点为内、外底板交线与舱段对称剖面的交点,J点为外底板的中心点,K点为内底板的中心点。舱段毁伤后,I、J、K三点分别移动到I′、J′、K′三点,其在竖直方向的位移分别为s、so和si。在此基础上,将s定义为舱段位移,内板挠度wi定义为wi=si-s,外板挠度wo定义为wo=so-s。
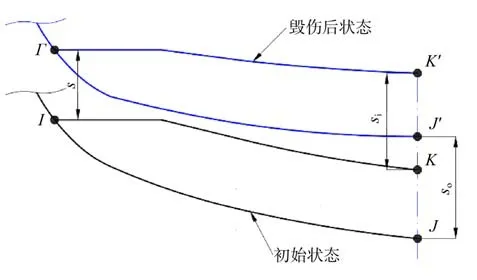
图7 舱段初始状态与毁伤后状态示意图Fig. 7 Schematic of initial state and damaged state of cabin
板的破口半径Rp定义为Rp=(dx+dy)/4,其中dx为破口在x轴方向上的最大撕裂宽度,dy为破口在y轴方向上的最大撕裂宽度,本文的模拟工况仅得到菱形和六边形破口,不同形状破口的最大撕裂宽度定义如图8 所示。
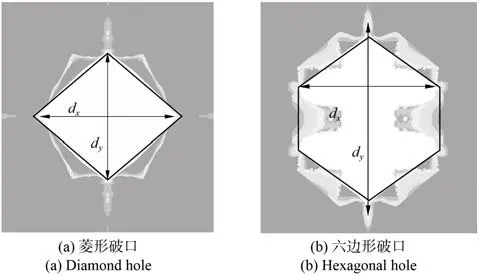
图8 破口最大撕裂宽度定义示意图Fig. 8 Schematic of the definition of maximum tear width
根据以上定义,得到了不同工况下内板最大挠度wim、外板最大挠度wom、破口面积S、破口半径Rp和舱段最大位移sm的结果,如表3 所示。
根据文献[23]中研究,当爆距R=R0,即药包与背空板接触放置时,计算背空板花瓣破口半径Rp的半经验公式可以表示为
式中:η=12.36%;W为装药量(kg);Em为炸药单位质量内能,对于 TNT 炸药而言,Em=4.4× 106J/kg;δ为板厚,δ=0.02 m;σ0为初始屈服应力,σ0=490.1 MPa;εf为失效应变,εf=0.25。工况1 中的外底板为背空板,并且爆距R=R0,按 式(5)估算破口半径Rp为2.68 m,数值模拟得到的破口半径为3.04 m,误差为13.4%,误差在可接受的范围之内。
3.3 不同爆距条件下毁伤特性分析
表3 中工况1~工况9 的爆距R从R0到5.0R0进行设置,板间水位h不变,进而研究爆距对双层底结构毁伤特性的影响。
3.3.1 工况1~工况3 的毁伤特性
对模拟结果进行对比分析发现,工况1~工况3的毁伤特性相似,下面对工况3 进行分析。图9 所示为工况3 中不同时刻气泡与双层板相互作用过程和内、外底板的等效塑性应变云图,每一幅图的左半部分为外底板与气泡的相互作用过程,右半部分为内底板与气泡的相互作用过程。由图9 可见:
1) 在t=2 ms 时,前导冲击波作用下外板首先出现小破口,由于破口大小的限制,气泡的膨胀过程变缓,呈现上尖下大的鸡蛋形,双层板间介质为空气,冲击波到达内底板时超压峰值严重衰减,未能使内板出现明显的塑性变形,如图9(a)所示。
2) 在t=8 ms 时,气泡逐渐被破口分割成外气泡和内气泡两个部分,外气泡在外底板下方持续膨胀,其膨胀过程受双层板的影响较少。而内气泡上表面与内底板接触,侧表面与外底板的破口接触,导致内气泡在膨胀过程中一方面使外底板破口持续增大,逐渐转化成花瓣型破口,另一方面使内底板开始的挠度增加,出现塑性大变形,如图9(b)和 图9(c)所示。
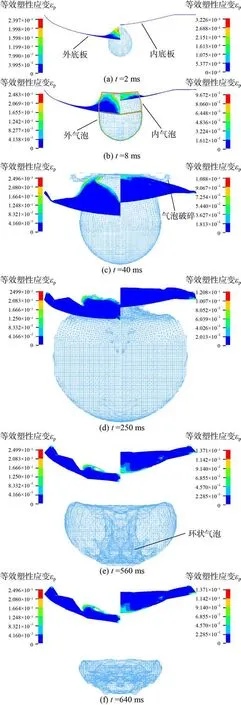
图9 工况3 不同时刻气泡与双层板相互作用过程Fig. 9 Interaction between bubbles and the double bottoms at different moments (Scenario 3)
3) 在t=40 ms 时,气泡逐渐破碎,气泡内部气体与双层板间气体联通,气泡内部气体压力减小,气泡的膨胀作用减弱,导致气泡在t=250 ms时就已经达到最大半径。之后气泡进入收缩阶段,t=560 ms 时,形成明显的环状气泡,逐渐形成向下的射流,该射流方向未指向双层板结构,因此对双层板不具有毁伤作用。
4) 大约在t=640 ms 时,气泡完成一个脉动周期,收缩到最小体积,而根据自由场气泡脉动周期经验公式(式(6))[24]计算得到的气泡脉动周期为 844 ms,模拟得到的气泡脉动周期较自由场气泡脉动周期小了24.17%。文献[20]的实验结果也表明,由于气泡内部气体与双层板间气体发生交换,使气泡脉动的动力降低,导致气泡在破口附近的脉动周期明显小于相同条件下的自由场脉动周期。
图10 所示为工况3 中舱段的位移和内底板挠度时程曲线。由图10 可以看出,内底板挠度约在t=90 ms 时就已经达到最大,之后开始收缩,约在t=600 ms 内板挠度再次开始增加,开始的时间与气泡脉动周期接近。综合图9 所示的气泡与双层板相互作用过程图可以看出,内底板挠度的第一次增加主要是穿过外板破口的内气泡的膨胀作用造成。在气泡膨胀的后期,气泡滞后流载荷向下,导致内底板挠度减少。之后由于涌流效应,双层板间水位增加,双层板间介质由原来的空气变成了海水,导致气泡的二次脉动压力波载荷可以传递到内底板,使内底板挠度再次增加。

图10 工况3 内板和舱段位移时程曲线Fig. 10 Displacementtime history curves of inner plate and cabin (Scenario 3)
由于舱段质量较大和周围水域的阻尼作用,导致舱段位移在冲击波加载阶段的增加速度较为缓慢,舱段位移约在t=420 ms 时达到最大。在气泡脉动二次压力波加载阶段,即t=640 ms 时,舱段位移再次增加,但增加不明显,因此气泡脉动二次压力波载荷对舱段位移的影响不大,而前导冲击波载荷和气泡脉动滞后流载荷对舱段位移起到决定性作用。
3.3.2 工况4 的毁伤特性
当爆距增加时,前导冲击波载荷减弱,双层板的毁伤特性与工况1~工况3 有所不同。图11 所示为工况4 中不同时刻气泡与双层板相互作用过程和内、外底板的等效塑性应变云图。
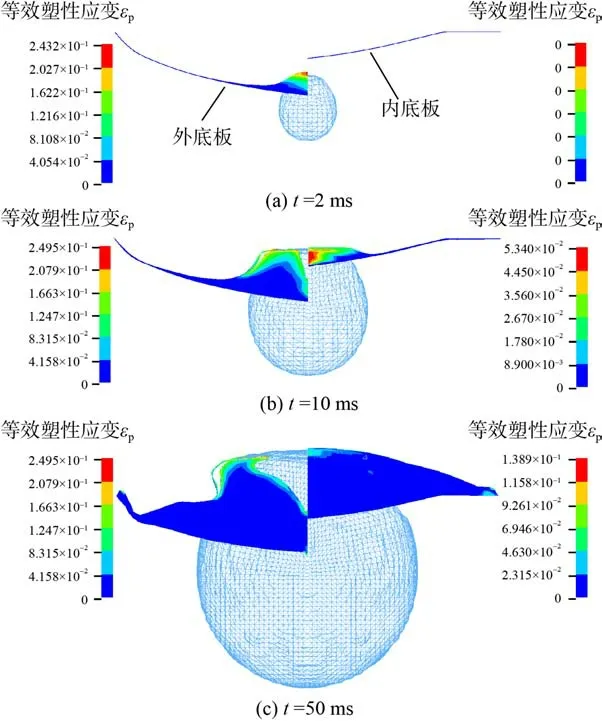
图11 工况4 不同时刻气泡与双层板相互作用过程Fig. 11 Interaction between bubbles and the doublebottoms at different moments (Scenario 4)
在t=2 ms 时,外板在冲击波作用下未出现破口,但外板中心处的等效塑性应变已经接近断裂应变0.25,如图11(a)所示。紧接着内气泡的膨胀作用使外板的等效塑性应变增加,中心处出现裂纹,进而逐渐演化成花瓣型破口,如图11(b)所示,与工况1~工况3 不同的是,气泡膨胀作用形成的破口花瓣个数为6 个,破口形状接近六边形,虽然破口的撕裂宽度较工况2、3 略小,但破口面积更大,导致后期的舱室涌流效应更加明显,舰船更容易丧失生命力。
3.3.3 工况8 的毁伤特性
当爆距进一步增加时,前导冲击波载荷进一步减弱,双层板的毁伤特性也发生变化。工况5~ 工况9 的毁伤特性相似,选择工况8 进行分析,如图12 所示。该工况下冲击波和气泡载荷均未使外底板出现破口,但随着气泡的膨胀,外板的挠度逐渐增加。当外板的变形量超过双层板间距时,内、外底板发生接触,导致内底板开始出现塑性变形。由于外底板未出现破口,导致气泡的膨胀作用不能直接作用到内板上,如图12(a)和图12(b)所示。

图12 工况8 不同时刻气泡与双层板相互作用过程Fig. 12 Interaction between bubbles and the double bottoms at different moments (Scenario 8)
3.3.4 不同爆距条件下的毁伤特性总结
图13 所示为工况1~工况9 中双层底结构的毁伤情况,包括内、外底板的挠度,外底板的破口面积和舱段最大位移。结合图9 和图11 可以看出,当爆距小于2 倍装药半径时,外底板破口由前导冲击波造成,且随着爆距的增加,破口面积有所减小,当爆距为2.5 倍装药半径时,外底板破口由气泡的膨胀作用造成,且破口面积更大。
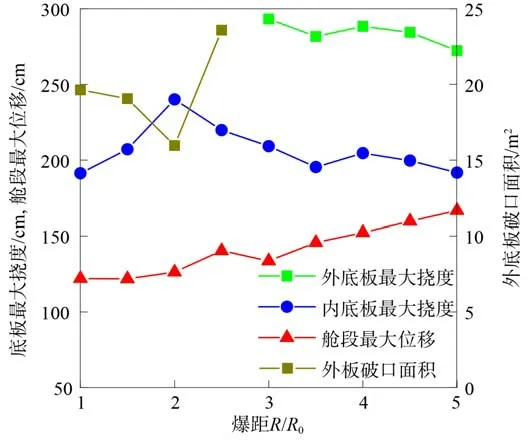
图13 不同爆距条件下结构毁伤情况Fig. 13 Damage to structure under different explosion distances
值得注意的是,当爆距小于2 倍装药半径时,内底板的挠度随着爆距的增加而增加。这是因为当爆距越小时,气泡在膨胀阶段进入破口的部分更多,气泡在双层板间破碎泄压更为严重,气泡能量过多的释放,导致气泡脉动压力波减小,气泡脉动压力波的加载作用减弱,如图14 和图15 所示。

图14 工况1~工况4 中气泡与破口 相互作用情况(t=2 ms)Fig. 14 Interaction between bubble and hole (t=2 ms, Scenario 1~4)
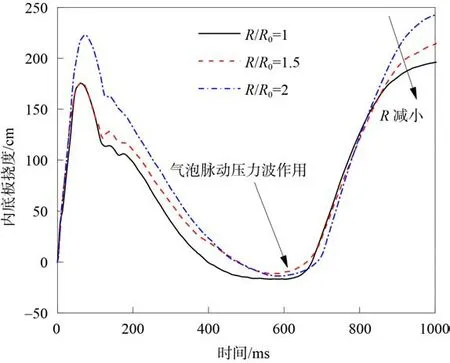
图15 不同爆距条件下内底板挠度时程曲线Fig. 15 Time-history curves of deflection of inner bottom under different explosion distances
当爆距大于2 倍装药半径时,内、外底板仅出现塑性大变形,且内、外底板的挠度值随爆距的增加呈现减小的趋势。当爆距为2 倍装药半径时(R/R0=2 时),内底板的挠度达到最大,当爆距为2.5 倍装药半径时(R/R0=2.5 时),外底板的破口面积达到最大,即存在最佳爆距使炸药对双层底结构的毁伤威力达到最大。
He 等[25]进行了TNT 炸药在不同爆距条件下对船体梁模型的毁伤实验,结果也表明:正如图13中数值模拟所体现的,确实存在使船体挠度值达到最大的最佳爆距,并且对应的最佳爆距与药包半径的比值R/R0≈3,而本文的数值模拟结果得到最佳爆距与药包半径的比值R/R0≈2.0~2.5。可以看出,文献[25]的实验结果与本文的数值模拟结果较为 一致。
值得注意的是,爆距在1 倍药包半径到5 倍药包半径之间时,舱段位移随着爆距的增加而增加,这是因为当爆距增加时,水下爆炸载荷对舱段的作用范围更大,使内、外底板的局部毁伤效应(花瓣破口、塑性变形)减弱,导致更多的水下爆炸能量转化为舱段动能。实际的水面舰船由若干舱段组成,舱段在水面上的整体运动导致舰船出现鞭状运动,当舰船的鞭状运动频率与其低阶固有频率接近时,舰船容易发生整体折断,使舰船丧失生命力。
3.4 不同板间水位条件下毁伤特性分析
表3 中工况1 和工况10~15 的板间水位h从 0 cm 到173 cm 进行设置,爆距R不变,进而研究板间水位对双层底结构毁伤特性的影响。
3.4.1 典型工况的毁伤特性
对模拟结果进行对比分析发现,工况1、10~工况15 的毁伤特性相似,外底板均在前导冲击波载荷作用下出现了花瓣破口,内底板均出现塑性大变形。下面取典型工况14 进行分析,如图16 所示。
由图16 可见:
1) 在t=2 ms 时,外板在冲击波的作用下出现较小的冲塞型破口,同时内气泡形成,呈现上窄下宽的蘑菇形。由于该工况下板间水位为125 cm,大于双层板间距,部分水域与内底板接触,导致前导冲击波载荷可以作用到内底板上,使内底板出现塑性变形,如图16(a)所示。紧接着内气泡的垂向膨胀使内底板挠度增加,横向膨胀使外底板的破口扩大,如图6(b)所示。
2) 在t=60 ms 时,内气泡继续膨胀,但此时气泡已经接近最大半径,气泡的膨胀作用减弱,难以使内底板挠度和外底板的花瓣破口面积继续增加,此时内气泡呈现出上宽下窄的手柄形,而外气泡继续保持球形,整个气泡出现缩颈现象,如图16(c)所示。随着气泡进入收缩阶段,内气泡向下转移,逐渐与外气泡分离,内、外底板受到气泡滞后流 载荷的作用,其挠度逐渐减小,出现负挠度,如 图16(d)和图16(e)所示。最后气泡达到最小体积,产生的二次脉动压力波作用到内、外底板,使其恢复正挠度,如图6(f)所示。
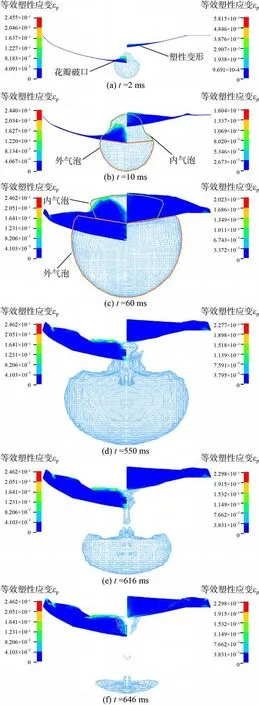
图16 工况14 不同时刻气泡与双层板相互作用过程Fig. 16 Interaction between bubbles and the double bottoms at different moments (Scenario 14)
3.4.2 不同板间水位条件下的毁伤特性总结
图17 所示为计算结束后工况1 和工况10~ 工况15 中结构的毁伤情况,包括内底板的最大挠度,外底板的破口面积和舱段最大位移。
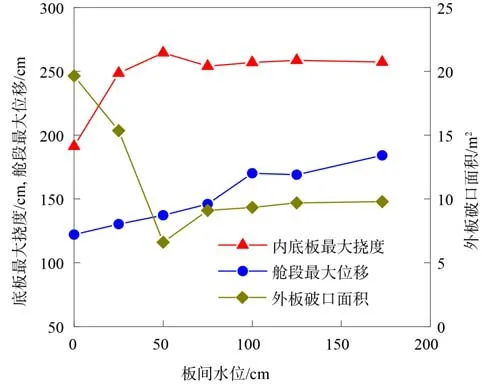
图17 不同板间水位条件下结构毁伤情况Fig. 17 Damage to structure under different water levels
由图17 可以看出,当双层板间水位h小于 50 cm 时,随着板间水位的增加,外底板的破口面积减小,内底板的挠度增加。这是因为当双层板间存在少量压载水时,外底板上方的水介质分担了爆炸载荷冲量给予外底板的动量增量,减弱了外底板花瓣破口的撕裂作用,使破口面积减小。而该部分动量增量又通过双层板间水介质,以冲击波的形式作用到内底板,使内底板挠度增加。
由图18 可以看出,当双层板间水位h大于 50 cm 时,随着板间水位的增加,内底板的挠度基本不变,而外底板的破口面积略微增加。这是因为当双层板间水位达到某一特定值时(小于双层板间距),在水下爆炸气泡膨胀作用下,双层板间空间减小,双层板间介质全部变为海水,因此内底板会受到前导冲击波载荷的作用。当板间水位进一步增加时,内底板受到的前导冲击波载荷不再明显增加,因此当板间水位达到某一特定值后,内底板挠度保持稳定,不再增加。

图18 不同板间水位条件下内底板挠度Fig. 18 Deflection of inner bottom under different water levels
4 结论
本文首先进行电火花气泡与带预制破口的双层底结构模型相互作用实验,并建立该实验的有限元数值模型,根据实验结果验证了数值模型的有效性。在此基础上建立了实尺度的舰船双层底舱段模型,通过改变爆距和双层板间水位,设置15 个数值模拟工况,探究了爆距和双层板间水位对舰船双层底结构在水下爆炸载荷下的毁伤特性的影响。得出主要结论如下:
1)当爆距小于2.5 倍装药半径时(双层板间水位为0 cm,即空舱),外底板在水下爆炸载荷下出现花瓣破口,爆炸气泡在破口处被分割成内气泡和外气泡,内气泡的膨胀速度大于外底板花瓣破口的撕裂速度,内气泡的膨胀作用加剧了外底板破口的撕裂,同时使内底板出现塑性变形。当爆距大于 2.5 倍装药半径时(双层板间水位为0 cm,即空舱),水下爆炸载荷不足以使外底板出现破口,内气泡无法形成,此时内底板的毁伤特性是:外底板发生大变形后,与内底板接触,外底板的变形带动了内底板的变形。
2)当双层板间水位小于50 cm 时(即爆距为 1.0 倍药包半径),前导冲击波载荷传递到内底板时会经过板间空气介质,导致冲击波载荷衰减较大,对内底板毁伤作用较小,此时内气泡的膨胀对内底板的变形起到主要作用。当双层板间水位大于 50 cm 时(爆距为1.0 倍药包半径),外底板的变形和破坏使板间水直接接触到内底板,前导冲击波载荷和气泡脉动二次压力波载荷衰减较小,二者能够共同通过水介质作用到内底板,使内底板产生变形。
3)当爆距在1 倍药包半径到5 倍药包半径之间时,舱段最大位移随着爆距的增加而增大(见 图12)。当双层板间水位在0 cm 到173 cm 之间时,舱段最大位移随着双层板间水位的增加而增大(见图16)。
4)在毁伤方面,当水下炸药距离舰船底部结构2.5 倍装药半径爆炸时,其毁伤威力达到最大。在防护方面,当双层板间的压载水位为50 cm,即双层板间距的一半时,对水下爆炸载荷的防御能力达到最强。上述研究可为舰船双层底部结构的毁伤与防护技术提供指导。

