如何用构造函数法解答含参不等式恒成立问题
陈正民

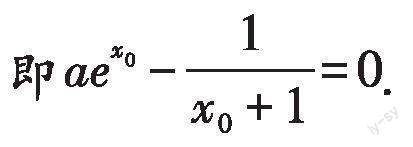
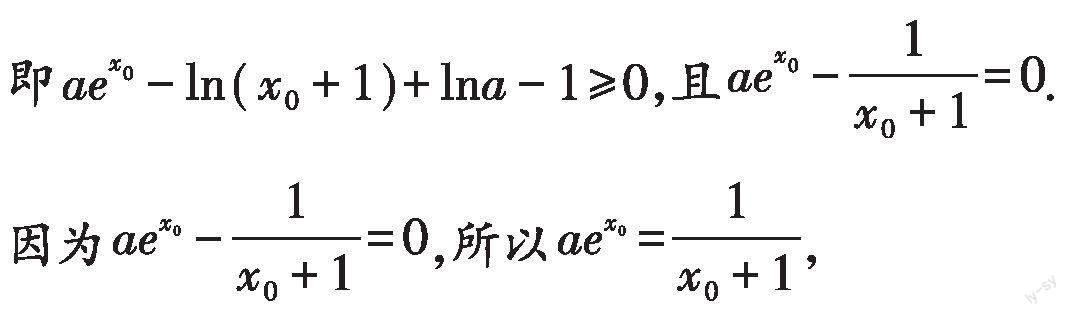
含参不等式恒成立问题通常较为复杂,侧重于考查同学们综合运用函数、不等式、导数、平面几何等知识解题的能力.解答此类问题的常用方法是构造函数法.那么,如何构造合适的函数呢?下面结合实例来进行探讨.
例题:若对于任意的[x>-1],不等式[aex-ln(x+1)≥1-lnaa>0]恒成立,求实数[a]的取值范围.
该不等式中含有指数式、对数式、参数,较为复杂,需灵活运用构造函数法求解.
一、通过移项构造函数
若不等式的两侧均含有代数式,则需将不等式两侧的式子进行移项,并将其一侧或两侧的式子构造成函数,即[f(x)>0、f(x)<0]、 [f(x)>g(x)、f(x) 解法1.由[aex-ln(x+1)≥1-lna]可得[aex-ln(x+1)+lna-1≥0]. 令[f(x)=aex-ln(x+1)+lna-1(x>-1)], 所以[f(x)]在[(-1,+∞)]上是单调递增的, 当[x][→-1]时, [f(x)→-∞];当[x→+∞]时,[ f(x)→+∞], 所以存在[x0∈(-1,+∞)],使得[f(x0)=0], 当[-1 所以[f(x)]在[(-1,x0)]上单调递减,在[(x0,+∞)]上单调递增, 所以[f(x)min=f(x0)=aex0-ln(x0+1)+lna-1], 要使[f(x)≥0]恒成立,须使[f(x0)≥0], 在上式的两边同时取对数, 得[lna=-x0-ln(x0+1)], 所以[g(x)]在[(-1,+∞)]上单调递减,且[g(x0)≥g(0)]. 不等式两边的式子中都含有对数式、参数,需将其左右两边的式子移项,这样便将不等式左边的式子构造成函数[f(x)=aex-ln(x+1)+lna-1(x>-1)].然后对函数進行两次求导,通过虚设零点,判断出函数的单调性,进而求得函数的最小值和参数的取值范围. 二、通过变更主元构造函数 在解答数学问题时,通常会将x、y视为主元,将其他变量视为参数.在解答含参不等式恒成立问题受阻时,不妨将x、y视为辅元、参数视为主元,来构造出新函数,以通过变更主元,将不等式恒成立问题转化为关于新元的函数最值问题来求解,从而轻松获得问题的答案. 解法2.由[aex-ln(x+1)≥1-lna]可得[aex-ln(x+1)+lna-1≥0]. 令[a=1],则[f(x)=ex-ln(x+1)-1(x>-1)], 所以[f(x)]在[(-1,0)]上单调递减,在[(0,+∞)]上单调递增, 所以[f(x)min=f(0)=0],即[f(x)≥0]. 所以[a=1]时,[ f(x)≥0]恒成立. 令[g(a)=aex+lna-ln(x+1)-1(x>-1)(a>0)], 所以[g(a)]在[(0,+∞)]上单调递增. 当[a≥1]时,[g(a)≥g(1)≥0],所以[f(x)≥0], 当[0 因为[0 可得[f(0)=(a-1)+lna<0],所以[0 综上可知,当[a≥1]时不等式恒成立. 我们先变更主元,将不等式中的参数a看作主元,构造函数[g(a)=aex+lna-ln(x+1)-1(x>-1)];然后对函数求导,而求导后的式子较为简单,只需分[a≥1]、[0 三、结合同构式构造函数 有时通过变形、化简、移项、添项、去项等,可以将不等式两边的式子变成结构一致、形式相似的式子,即同构式,此时可根据同构式的结构特征,构造出函数模型,将不等式两边的式子看作不同自变量的函数值.那么我们只需判断出函数的单调性,或求得函数的最值,即可建立新不等式,从而快速求得参数的取值范围. 解法3.由[aex-ln(x+1)≥1-lna]可得[aex+lna≥ln(x+1)+1]. 因为[a=elna],所以[ex+lna+lna≥ln(x+1)+1], 在不等式的两边同时加上[x], 得[ex+lna+(x+lna)≥ln(x+1)+(x+1)]. 令[f(x)=lnx+x(x>0)], 则[f(ex+lna)≥f(x+1)], 所以[f(x)]在[(0,+∞)]上单调递增. 因为[f(ex+lna)≥f(x+1)], 所以[ex+lna≥x+1], 当[-1 当[x>0]时,[g(x)]在[(0,+∞)]上单调递减, 所以[g(x)max=g(0)=1], 所以当[a≥1]时,不等式恒成立. 将不等式移项,并在其左右两边的式子上同时加上x,即可得到同构式[ex+lna+(x+lna)、ln(x+1)+(x+1)].然后根据同构式,构造函数[f(x)=lnx+x(x>0)],通过研究其导函数,判断出函数的单调性,求得其最值,即可解题.在构造同构式时,同学们要仔细观察不等式的结构特征,发现其共同点,对其进行合理的变形、配凑. 由此可见,运用构造函数法解答含参不等式恒成立问题,关键是通过移项、变更主元,结合同构式的特征,构造出合适的函数模型,这样才能将复杂的题目转化为简单问题来求解,从而达到化难为易的目的.

