GNSS 外辐射源雷达低慢小目标探测概率

苗铎，杨东凯，许志超，王峰，吴世玉

(北京航空航天大学 电子信息工程学院，北京 100191)

近年来，随着科学技术的不断发展，传统单基地雷达面临着电磁干扰、低空/超低空突防、高速反辐射导弹、隐身飞机等威胁，无法有效应对新技术和新方案的挑战[1]。外辐射源雷达作为一种双/多基地无源雷达，具有隐蔽性强、成本低、可用信号源丰富等优点，已成为雷达领域的研究热点之一。20 世纪90 年代末，美国洛克希德·马丁公司以调频广播(frequency modulation, FM)信号作为外辐射源，推出了成熟适用的商用被动雷达“沉默哨兵”[2-3]。目前外辐射源雷达所使用的非合作外辐射源主要有FM 信号[4]、数字电视信号[5]、全球移动通信信号[6]及导航卫星信号[7]等。在各类外辐射源中，全球导航卫星系统 (global navigation satellite system，GNSS)因信号源广泛、覆盖率高、易进行时间同步等特点，使得针对该技术的研究日益增多。

双基地雷达的几何构型复杂多变，主要分后向和前向探测模式。后向探测模式与传统单基地雷达探测模式类似，利用反射回波中携带的目标时延及多普勒信息检测目标。相比于后向探测模式，前向散射雷达(forward scattering radar, FSR)可以提高目标的雷达散射截面积（radar cross section, RCS），在反隐身探测领域具有重要意义，成为了一项新的研究方向[8]。英国伯明翰大学微波集成系统实验室(microwave integrated systems laboratory, MISL)近年对前向散射雷达开展了一系列研究，完善了地面、海洋及空中目标探测的理论基础[9-15]。北京理工大学自2006 年起与伯明翰大学MISL 开展联合研究，在前向散射雷达的杂波分析、运动目标参数估计及多目标分辨特性等问题上取得了一定的研究进展[16-18]。尽管基于外辐射源雷达目标探测的基础理论已逐渐成熟，但探测模式单一且存在一定的局限性，限制了外辐射源雷达的探测性能和使用环境，尤其由于GNSS 外辐射源雷达的信号源并非固定辐射源，使得某些时刻可用的辐射源较少，单一模式的探测难以满足实际的探测需求，漏警率较高。

本文以“低慢小”飞行器作为典型的探测目标，统计分析GNSS 无源雷达在不同单一探测模式下目标探测概率，针对在单一模式下探测概率较低的问题，提出多辐射源融合及前后向协同探测模式，并分析协同融合的外辐射源雷达目标探测性能。

1 双基地角与目标雷达散射截面积的关系

1.1 GNSS 无源雷达双基地角

在实际探测场景中，双基地角 β是一个受多因素影响的复杂三维空间变量。GNSS 无源雷达的空间几何构型如图1 所示，其中选取地面基站的接收天线作为原点O，天线照射方向在地平面上的投影作为y 轴建立三维空间坐标系，图中：S′为卫星S 在yOz 平面的投影，ϕT为卫星与yOz 平面的夹角，RT为 卫星辐射源到目标的距离，RR为目标到地面基站的距离，L 为卫星辐射源到地面基站的距离，β为双基地角，θT为 卫星仰角，θR为地面基站接收天线在yOz 平面的照射方向，β′为 双基地角 β在yOz 平面的投影。

图1 双基地雷达三维空间几何构型Fig.1 Three-dimensional geometric configuration of bistatic radar

1.2 目标雷达散射截面积

由于通过电磁理论精确计算目标RCS 十分困难，因此，在仿真过程中采用近似计算的方法来估计复杂目标RCS。常用近似计算方法有物理光学法(physical optics, PO)、几何光学法(geometrical optics, GO)、物理绕射理论(physical theory of diffraction, PTD)、几何绕射理论(geometrical theory of diffraction, GTD)、矩量法(method of moments, MOM)等[20]。矩量法将被探测目标分割成多个小部分，用标准的矩阵代数求解麦克斯韦积分方程组，实现目标RCS的解算。相比于其他方法，由于该方法求解积分方程的使用限制更小，可应用在多种情况的近似计算中，因此，本文采用矩量法进行“低慢小”目标RCS的计算。为简化仿真计算的复杂度，选取如图2 所示的金属圆柱体作为“低慢小”飞行器的近似模型，其中圆柱体半径r=0.27 m，高度h=0.3 m；入射波为频率1 176.45 MHz 的GPS L5 信号，沿z 轴负半轴方向进行照射；双基地角 β取值范围为0°～360°。仿真过程中仅考虑入射波和散射波形成的双基地角对双基地RCS 的影响，忽略因目标姿态角变化引起的RCS 变化。

图2 金属圆柱体模型Fig.2 Metal cylinder model

图3 为仿真的GNSS 信号左右旋极化的目标RCS 随双基角的变化曲线。目标再辐射的GNSS散射信号发生了极化变化，由右旋圆极化波转变成椭圆极化波。随着双基地角 β的变化，椭圆极化波的轴比不断改变。在后向散射区域散射波以左旋圆极化波为主，应采用左旋天线接收，且随着双基地角增大，目标RCS 呈下降趋势，即在后向模式中应尽量选取双基地角较小的几何构型进行目标探测。在前向散射区域散射波以右旋圆极化波为主，应采用右旋天线接收，且随着双基地角的增大，目标RCS 呈上升趋势，在双基地角接近180°时达到最大。此外，通过对比可看出前向模式下目标RCS较后向模式高。

图3 不同极化情况下的RCS 仿真结果Fig.3 RCS simulation results under different polarization conditions

2 GNSS 外辐射源雷达探测性能

相比于GPS L1 信号，GPS 卫星发射的新型民用信号GPS L5 信号的发射功率更高、频带宽度更宽且引入了不含数据调制的导频通道，使其更适合作为目标探测的外辐射源[21]。在不考虑传播损耗的情况下，地面基站接收天线所接收的信号功率为[22]

本文选取“低慢小”飞行器作为典型目标，假设RCS 为5 m2，接收天线增益为25 dB。当目标检测所需最低信噪比为8 dB 时，目标最大检测距离与积分时间及非相干累加次数的关系如图4 所示。从图4 可知，随着相干积分时间及非相干累加次数的增加，最大探测距离不断提高。由于目标出现在探测区域的时间有限，积分时间并不能无限增大。通常将该目标的出现时间作为最大检测时间，以限制数据处理过程中的相干积分时间与非相干累加次数。最大检测时间可表示为相干积分时间与非相干累加次数的乘积 Tdet=TintN。受目标飞行速度、飞行姿态、接收天线波束角范围等因素约束，通常以约1 s 的检测时间对大多数民用交通为最佳[23]。选取L5 信号导频通道的Neuman-Hoffman同步码(NH 码)周期(20 ms)作为相干积分时间，最大处理时间为1 s，则非相干累加次数为50。选取“低慢小”飞行器作为典型目标，代入式(12)计算可得最大探测距离为674.29 m。

图4 最大探测距离随积分时间及非相干累加次数的变化Fig.4 Variation of the maximum detection distance at different integration time and incoherent accumulation times

3 “低慢小”目标的探测概率

3.1 目标的探测概率

式中：v 为不完全伽马函数的积分变量。

图5 为虚警概率 Pfa=1×10-6，非相干累加次数为50 时，目标检测概率随SNR 的变化。从图5中可看出，在累加次数一定的情况下，目标检测概率与接收信号SNR 成正比例关系。通常认为当目标检测概率达到90%时可实现目标的有效探测[24]，此时所需的接收信号的SNR 约为8 dB。

图5 目标检测概率随SNR 的变化Fig.5 Variation of target detection probability with SNR

实际探测过程中，信噪比难以被直接观测，由式(11)可知，在一定条件下SNR 是目标最大探测距离的函数。假定所选探测目标RCS 为5 m2，接收天线增益为25 dB，虚警概率 Pfa=1×10-6，图6 为目标检测概率随最大探测距离的变化。随着最大探测距离的增加，目标的检测概率不断下降，当检测概率低于90%时可以认为在该距离下无法有效检测到目标。对比不同累加情况下的变化曲线，不进行累加情况下，最大探测距离不足100 m；单独进行20 ms 的相干积分和50 次的非相干累加时，最大探测距离可以提升到200 m 左右；2 种累加方法共同作用时，目标的最大探测距离超过600 m，探测性能得到了有效提升。

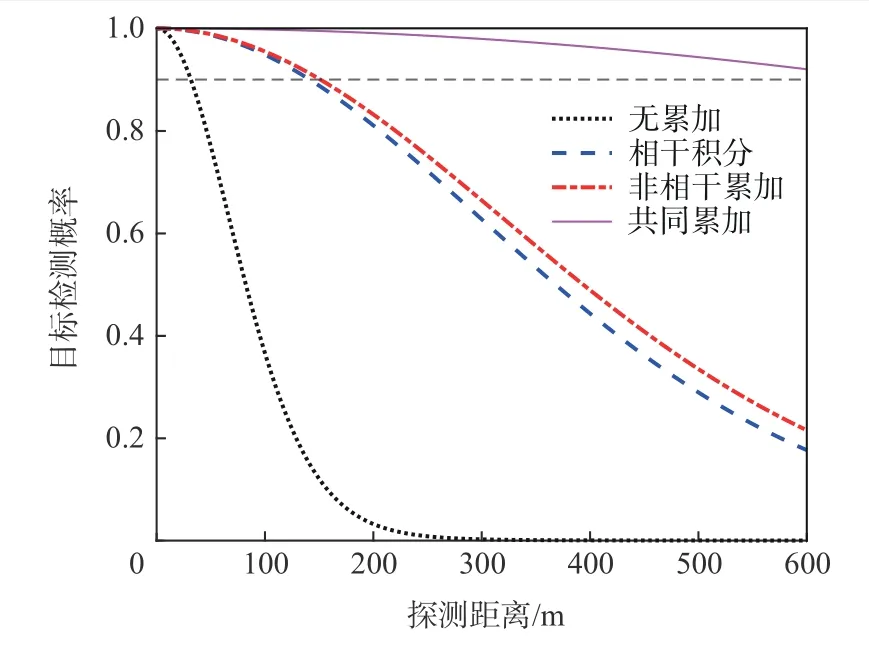
图6 目标检测概率随探测距离的变化Fig.6 Variation of target detection probability with detection distance

另一方面，将式(10)代入式(16)可知，目标检测概率是关于RCS 的函数。当其他条件固定时，目标检测的概率将随双基地角的变化而改变，即几何构型直接影响到双基地雷达的目标检测性能。以图2 所示仿真模型作为“低慢小”目标，接收天线增益为25 dB，相干积分时间为20 ms，非相干累加次数为50，计算不同目标探测距离下目标检测概率随双基地角的变化情况，结果如图7 所示。随着探测距离的提升，目标探测概率减小。当目标探测距离相同时，检测概率随双基地角改变呈现出先下降后上升的变化趋势。在后向散射情况下，较小的双基地角可实现对目标的有效探测，随着双基地角的提高，检测概率逐渐减小；当形成前向散射的几何构型后，目标检测概率随着双基地角的增加呈递增趋势，在双基地角为180°时取得最大值。当目标探测距离为500 m 时，后向散射模式满足有效探测的双基地角范围为0°～20°，前向散射情况下对应的双基地角范围是161°～180°，即约21.67%的双基地角条件可满足有效探测需求，实际探测中需要准确配置几何构型以提高雷达探测性能。

3.2 单颗卫星的有效探测时间覆盖率

为模拟卫星在一天内的双基地角变化情况，需设定模拟实验地点及实验日期，通过仿真实验区域的坐标信息，结合精密星历计算得到卫星在任意时刻的双基地角大小。截止到2020 年12 月31 日，发射GPS L5 信号的在轨卫星共有16 颗。选取模拟观测地点为北京首都国际机场，经、纬和高分别为116.614 3 °E、40.055 4 °N 和 50 m。模拟观测日期为2021 年3 月16 日。根据GPS 官方提供的精密星历计算每颗卫星在24 h 内的双基角变化。选取模拟探测目标为图2 所示的仿真目标，接收天线增益为25 dB，相干积分时间为20 ms，非相干累加次数为50，目标探测距离为500 m。一天内前后向散射模式下单颗卫星的目标探测概率统计如图8所示。统计结果显示在后向散射模式下单颗卫星能实现有效探测的情况仅占全天时间的0.26%，而前向散射模式下有效探测的时间覆盖率为0.52%。这说明采用单颗卫星进行目标探测时，一天内仅有极少数几何构型满足实际探测需求，须严格设计接收天线的位置及朝向获得最优探测效果。在后向散射模式下大部分时间内L5 卫星同目标和接收天线构成的双基地角较大，使得目标双基地RCS 较小，不足以实现有效探测。前向散射模式对几何构型要求更严格，据统计在单星情况下全天仅有4.95%时间可满足前向散射模式双基地角要求，无法充分发挥前向散射高目标RCS 优势，使得整体探测概率较低。

图8 单颗卫星的目标探测概率Fig.8 Target detection probability of a single satellite

3.3 多辐射源融合的有效探测时间覆盖率

由3.2 节结果可知单颗卫星的目标检测性能较差，无法满足“低慢小”目标的探测需求。多辐射源融合是提升目标探测性能的可靠方案。在目标探测过程中将每颗卫星看作独立的辐射源进行探测，不同卫星的信号可通过其伪随机码（pseudo random noise，PRN）进行区分，多辐射源的探测过程可假设为一个独立分布的随机过程。由于每颗星的位置不同，同一时刻其构成的双基地角不同，导致不同辐射源下目标的双基地RCS 不同，探测结果存在差异。多辐射源融合指的是将多颗卫星单独的探测结果进行叠加，取并集得到探测结果，即对探测结果进行了逻辑或运算，其探测概率可表示为

式中：Pdi为单颗卫星的目标检测概率。在后向散射模式下进行多源融合的目标探测，其探测概率统计如图9 所示。相比于图8 的单星检测结果，多辐射源融合后的目标探测概率明显得到提升。多源融合的后向散射模式在全天内有8.33%的时间可实现有效探测，而前向散射模式的有效探测的覆盖率可达到11.46%，极大地提高了目标检测概率，有效提升了目标探测性能。

图9 多源融合的目标探测概率Fig.9 Target detection probability with multi-satellites

3.4 前后向协同的有效探测时间覆盖率

在单一探测方式下后向模式由于目标本身的双基地RCS 较小，探测概率受到了较大程度限制。前向模式的目标探测概率受限于前向散射构型的覆盖率。如图9 所示，多源融合后一天内可以形成前向散射结构的时间仅占61%，使得有效探测的时间覆盖率仅达到11.46%，整体探测性能有限。前后向协同探测方式可充分发挥GNSS 外辐射源雷达的探测性能。前后向协同的探测模式的多源融合目标探测概率统计如图10 所示。利用前后向协同的多源融合探测方式，目标探测性能进一步提升，有效探测的时间覆盖率可达25%，极大程度减小了几何构型对目标探测场景的制约，使GNSS 外辐射源雷达的性能得到充分发挥。

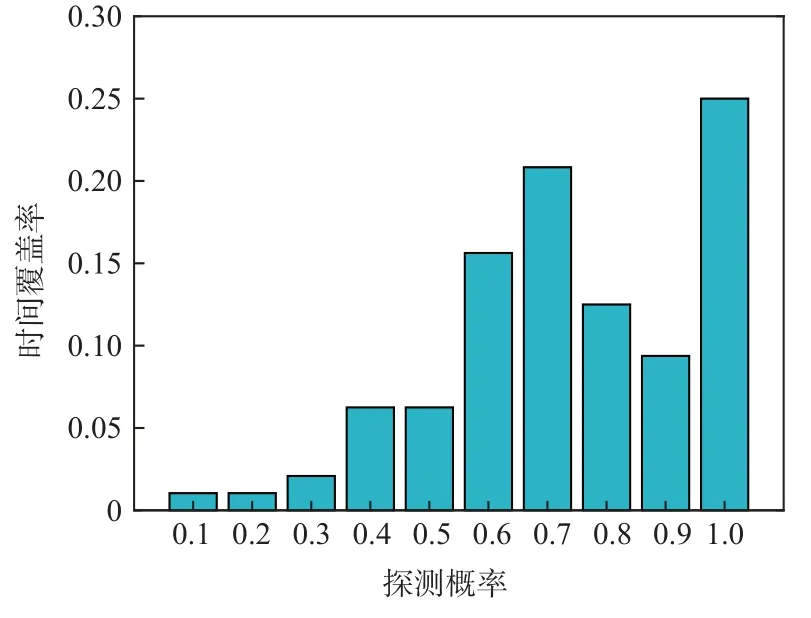
图10 前后向协同情况下多源融合的目标探测概率Fig.10 Target detection probability under backscattering and forward scattering condition with multi-satellites

3.5 连续扫描式检测的有效探测时间覆盖率

根据3.2 节～3.4 节的结论可以看出，当天线照射方向固定时，进行有效探测的时间覆盖率并不理想。为了实现目标的连续检测，可以根据卫星所在的方位，实时改变天线照射方向以提高目标的检测概率，即在后向散射模式下使卫星与天线照射方向所成的方位角为0°，前向散射模式下使方位角为180°。图11 为单星单基情况下，采用连续检测方式对全天的目标探测概率统计结果。在该情况下，后向散射模式有效探测的时间覆盖率提高到7.23%，前向散射模式下时间覆盖率提高到8.27%。可以看出实时改变天线照射方向确保在最优几何构型下进行目标探测时，检测性能得到了有效提升。

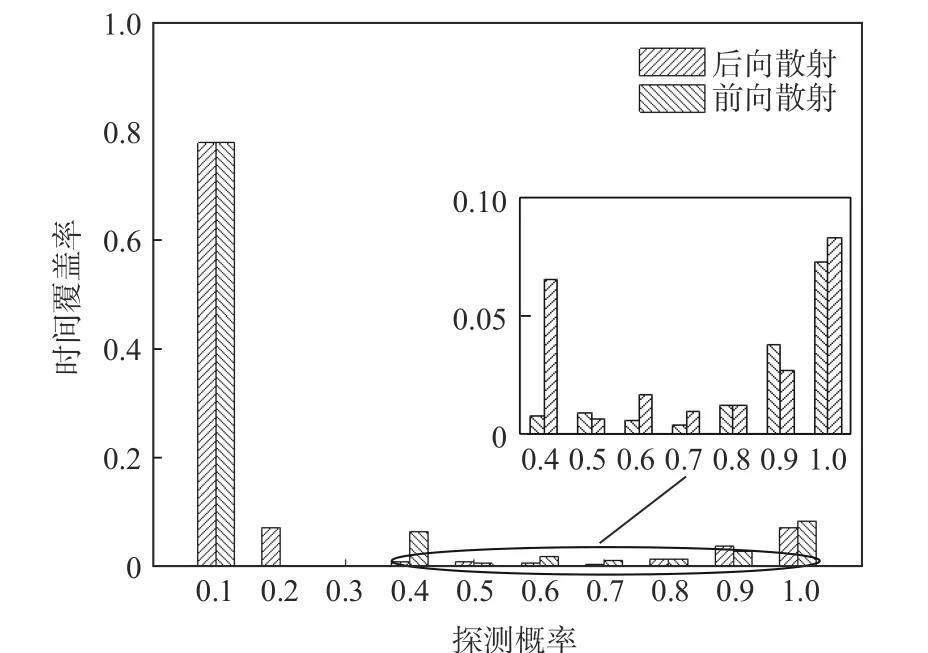
图11 连续检测情况下单颗卫星的目标探测概率Fig.11 Target detection probability under continuous detection of a single satellite

图12 为在多源融合的情况下实时改变天线位置进行连续扫描检测时有效探测的时间覆盖率。结果显示在后向散射模式下多源融合的连续扫描检测目标的有效探测时间覆盖率可达80.21%，前向模式下达88.54%；通过前后向协同有效探测的时间覆盖率可达98.96%，基本实现了全天时的有效探测。值得注意的是连续扫描检测实现多源融合需要依靠多接收天线协同工作，无疑增加了系统和算法复杂度。

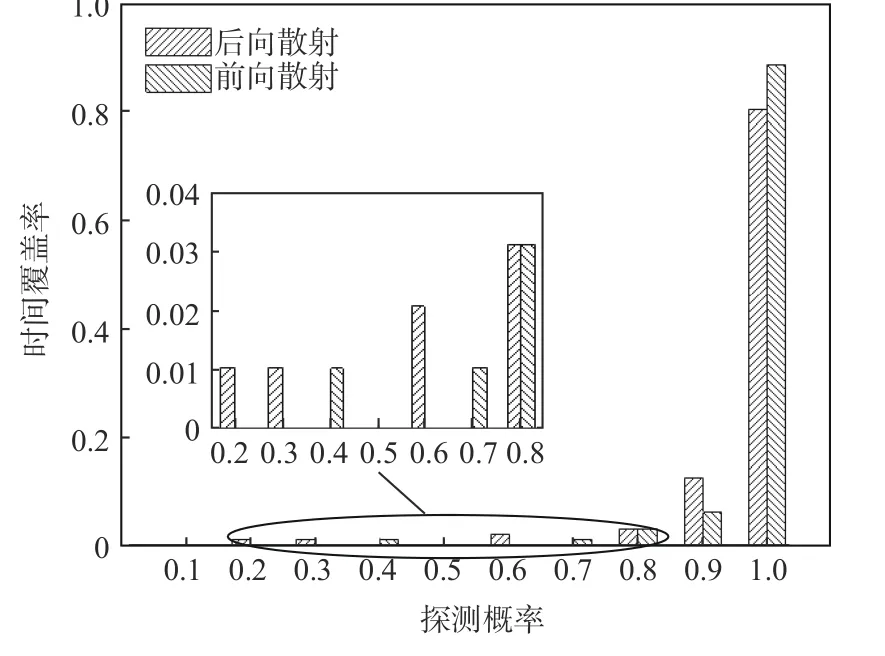
图12 连续检测情况下多源融合的目标探测概率Fig.12 Target detection probability under continuous detection with multi-satellites

4 结 论

1）后向散射模式以左旋圆极化散射波为主，而前向以右旋圆极化波为主。在建立的近似模型基础上，利用Swerling 起伏模型，计算了不同情况下GNSS 外辐射源雷达的目标检测概率，研究了多辐射源融合及前后向协同探测对于目标检测概率的提升作用。单星情况下目标检测性能较低，有效探测的时间覆盖率不足1%；通过采用多星融合及前后向协同可将有效探测的时间覆盖率提高至25%。通过卫星位置对天线照射方向进行实时调整，使系统以连续扫描的模式进行工作，单星及多源融合下有效探测的时间覆盖率得到了极大提升，在前后向协同的多源融合探测模式下，有效探测的时间覆盖率可达98.96%，基本可满足全天时检测的需求。

2）由于实际目标的双基地RCS 计算复杂，除外辐射源的照射方向引起的双基地角变化之外，目标的具体形状、表面材料及运动姿态均会影响双基地RCS。

本文旨在研究多源融合对目标探测概率的提升效果，仅采取简易模型进行了近似分析。在后续研究中将针对具体目标进行更精确仿真建模及分析。此外本文选用的卫星辐射源为GPS L5 信号，仅16 颗卫星在轨。随着GPS 现代化和北斗-3 系统的全面建成，在轨高带宽卫星信号的增大，GNSS 外辐射源的目标探测性能将进一步提升。