一种基于组合赋权法的小波去噪质量评价方法

李晋斐，赵冬青，王栋民，蔡聪聪，贾晓雪，张乐添

(信息工程大学 地理空间信息学院，郑州 450001)

在多传感器融合定位中，由于惯性导航系统能够持续输出姿态和位置信息，一般多以惯性导航误差模型建立状态方程。惯性元件随机误差对惯性导航系统产生的影响较大，因此需有效降低惯性元件的随机误差，达到提高惯性导航系统测量精度的目的。小波变换具有在时域和频域同时表征局部特征的能力[1]，采用多分辨率特性，使得去除噪声的过程中保持原始信息，能够很好地刻画信号的非平稳特征，且不需要建立精确的随机误差模型，即可分析处理非平稳信号，故非常适用于处理陀螺的状态信息[2]。

所有小波去噪算法都有共同的结构，但其有效性非常依赖相关参数的选择，主要涉及小波基函数、阈值选取规则、阈值函数、分解尺度等[3]。该过程中，很多学者关注了如何改进阈值函数来提高去噪能力，并取得了一定效果，而对于其他参数的选择却十分困难[4]，更多的是以经验或直接给定参数来得到最终结果，很少分析这些参数对最终效果的影响，也没有明确的小波基函数与分解层数等最优参数的确定方法。例如，对于惯性元件随机误差的小波去噪参数，文献[5]直接选定db4 小波基，3 尺度分解；文献[6]直接选定db6 小波基，5 尺度分解。然而，根据多次实验对比发现，采用小波去噪时，去噪效果随着每个尺度下所选择的小波变化而变化，很难直接确定分解层数；而分解层数与小波基函数的选取对去噪效果的影响不可忽略。要使去噪效果最好，必须选择最佳的小波参数，通常选择信噪比（signal-noise ratio，SNR）、相关系数 R、均方根误差（root mean square error，RMSE）、平滑度r等参数作为指标来衡量小波去噪效果[7]。在实际应用中，由于信号真值是未知的，上述单一的评价标准通常无法准确判断去噪效果，具有很大的局限性。因此，陶珂和朱建军[8]通过融合去噪过程中信号RMSE、SNR 和平滑度的变化量构造具有收敛特性的新统计量，通过识别拐点判断最佳分解尺度。朱建军等[9]通过变异系数法进行定权，选择信号的平滑度与RMSE 2 种指标进行组合，进而指导小波去噪相关参数的选择。王旭和王昶[10]利用熵权法将RMSE 与平滑度变化量线性组合得到复合评价指标，利用其收敛特性确定最优分解层数。实际计算表明，在真值未知时，这些方法都有较好效果，但在准确度上存在不同程度的缺陷，且在判断收敛性方面缺乏相应的理论依据。因此，本文构建了一种新的评价指标，并通过对惯性元件随机误差的分析，验证其在小波降噪过程中对相关参数选择的有效性。

1 小波阈值去噪质量分析

小波阈值去噪算法的实质是抑制信号的无用部分，最大限度保留信号的有用部分。利用小波分析的多尺度特性，把含有噪声的信号分解到多个尺度上，再在每一尺度上分别设定对应的阈值，其中，将噪声信号归纳为小于该阈值的小波系数，将有用信号归纳为大于该阈值的小波系数，分别去除各尺度上的噪声信号，同时保留有用信号，即可重构出去噪后的信号[11]。可以看出，同阈值函数一样，小波基函数和分解层数的选择对小波阈值的去噪结果也有很大影响。

1.1 小波阈值去噪模型

一个含噪声的一维信号可表示为[12]

式中：f(t)为 含有噪声的信号；s(t) 为 纯净信号；σ为噪声标准差；w(t)为噪声信号。

有用信号一般为低频信号，而噪声通常为高频信号。例如，对原始信号进行3 层分解：

式中：cAi为 分解的近似部分，cDi为分解的细节部分，i =1,2,3，噪声部分通常包含在c D3、cD2、cD1中。

总结去噪过程，主要包括以下3 个步骤[13]：

1）对原始信号进行小波分解。选择最佳的小波基和分解层数，将原始信号进行多尺度分解得到相对应的小波系数。

2）小波分解阈值量化。选择相对应的阈值及阈值函数，对小波系数进行阈值量化处理。

3）小波系数重构。将阈值化处理后的小波系数进行重构，得到去噪后的信号。

从上可知，最优的小波阈值去噪方案，不仅与阈值函数的选取有关，小波基函数、分解层数的选择都直接影响信号去噪的质量，而对于小波基函数与分解层数的选择大多基于经验或直接给定得到，未充分分析其对去噪效果的影响，如果能选择最优的小波基函数和分解层数，对于提高去噪效果将会有明显的帮助[14]。

1.2 小波去噪质量评价指标

小波基函数及分解层数都直接影响小波去噪效果，而使用不同的小波基与分解层数，去噪后的效果也不相同。如果分解尺度过小，则信号中仍存在较多的噪声数据，无法获得理想的去噪结果；如果分解尺度过大，则会将信号中的部分细节信息当做噪声删除，容易造成信号失真，同时增加计算复杂度，而去噪效果却没有显著改善[15]。因此，在去噪效果和分解层数之间找到平衡非常重要，需要构建一种全面的质量评价指标来衡量去噪效果。

当前，RMSE、SNR、平滑度r 等指标常被用于分析小波去噪的效果[16]。RMSE 指去噪信号与原始信号之间方差的平方根，其值越小说明去噪效果越优；SNR 是原始信号功率与噪声信号功率之间的比值，其值越大说明去噪效果越优[17]；平滑度是去噪信号一阶差分与原始信号一阶差分之间方差根比值，代表信号整体的变异信息，其值越小说明去噪效果越优。

为了评估这些指标的有效性，本文采用一组真值已知、小波去噪专用的测试数据即多普勒信号和一组真值未知的陀螺输出数据来进行小波分析，同陀螺信号类似，多普勒信号是一种非平稳信号，在原始信号上加入8 dB 的高斯白噪声，以及系数为0.1 的随机游走，信号长度为1 024 个点，采样频率为1 Hz。由于已知未加噪声的纯净信号，可求得重构信号与理论纯净信号的RMSE 及SNR，当RMSE最小且SNR 最大时，所配参数即为最佳的去噪参数。真实信号为采集的加拿大诺瓦泰公司SPANISA-100C 型高精度光纤惯导的静态陀螺数据，时长为5 h，采样频率为200 Hz。利用上述评价指标来判断最优分解层数，对于2 类信号，都以sym 4 作为小波基函数，分解层数为2～10。图1 为真值已知情况下多普勒信号小波去噪的质量评价结果，从RMSE 和SNR 结果中可以看出，最优分解层数为6 层，平滑度无法判定。图2 为真值未知情况下陀螺输出数据小波去噪的质量评价结果，此时无法找出最优分解层数，这是因为所测信号的真值是未知的，参与计算的是含有噪声的原始信号与去噪信号，如果未去掉任何噪声或去噪效果差，但得到的RMSE 值却很小，SNR 值很大，这与评价依据不一致，纵然平滑度是减小的，但却无法判断最优层数。通过分析可得在真值未知情况下3 种评价指标特点如表1 所示。

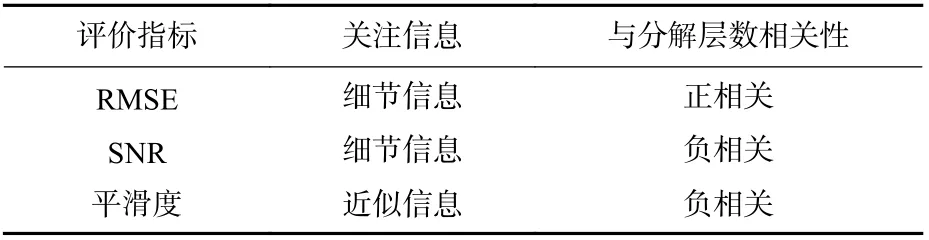
表1 真值未知时评价指标特点Table 1 Characteristics of evaluation indexes when truth value is unknown

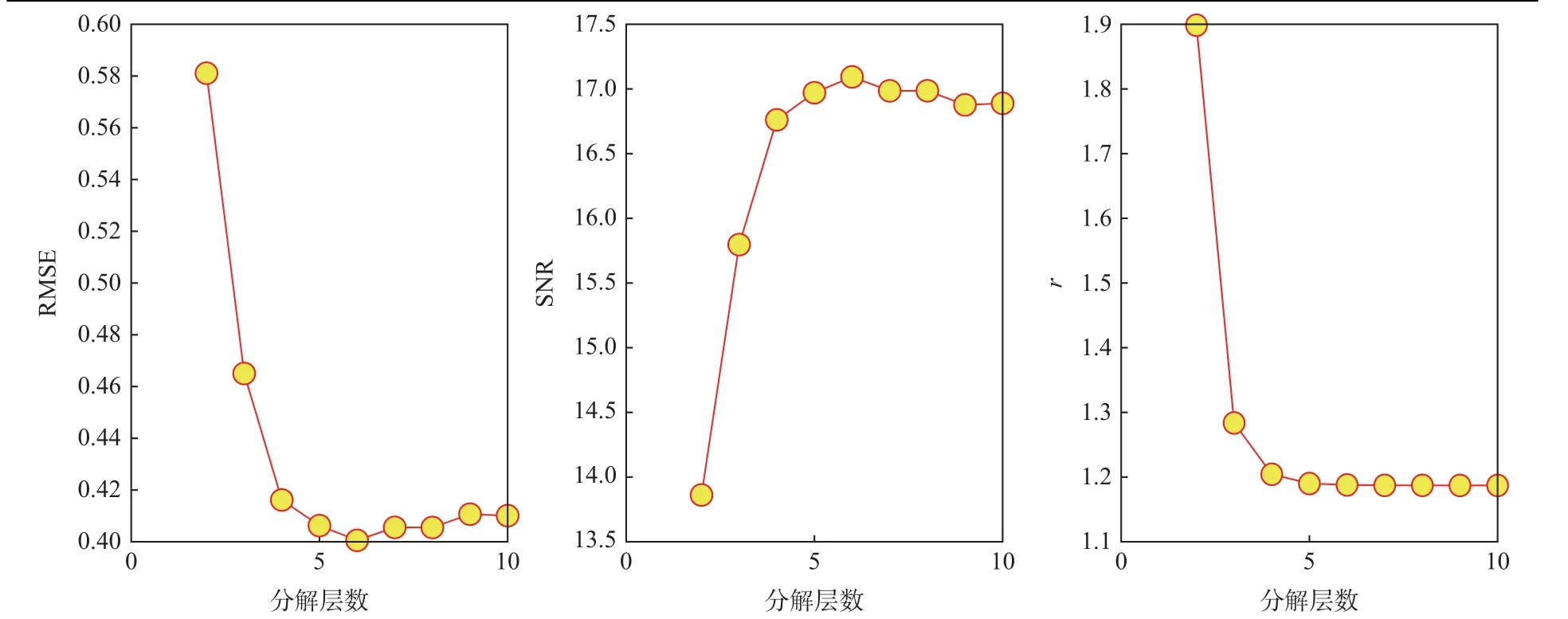
图1 真值已知的多普勒信号的单一评价指标趋势Fig.1 Trends of single evaluation index of Doppler signal with known truth value

图2 真值未知的陀螺输出数据的单一评价指标趋势Fig.2 Trends of single evaluation index of gyro output data with unknown truth value

因此，单一的评价指标具有一定的欺骗性，难以满足惯性元件误差分析的需求。若将多类评价指标进行赋权融合，以更加全面的视角来构建复合评价指标，从而满足在真值未知情况下小波去噪参数的选择。

2 复合评价指标构建

考虑到模型需简单且具有可行性，根据RMSE、SNR 及平滑度的几何与物理意义，选取RMSE 与平滑度2 个指标来构建复合评价指标。主要原因在于：RMSE 和SNR 都是关注信号的细节信息，而平滑度关注的是信号近似信息，为反映去噪信号的整体特征，应使用平滑度指标，同时，考虑到第1 节实验中SNR 值与平滑度值随分解层数的增加都减小，而RMSE 值随分解层数的增加而增大，故用平滑度与RMSE 构建复合评价指标。随着分解层数不断增加，必定出现一个极值，即去噪信号的近似信息与细节信息达到了最优的组合，对应的是最优分解层数。

由于RMSE 与平滑度值变化的范围不同，先将其归一化[18]，使2 个指标都处于[0,1]区间。归一化算法为

式中：PRMSE和 Pr分别为归一化后RMSE 和平滑度的值；m in和 max分别为最小值和最大值函数。

由于这2 个指标对信号特征的描述程度不同，在复合过程中权重也不一致，需要进行赋权处理。目前，有关评价指标权系数的确定方法很多，主要分为主观赋权法、客观赋权法、主客观集成赋权法3 类[19]，其中客观赋权法主要以其强大的数学理论做支撑，相比其他方法更加可靠。本文基于信息熵权法和变异系数法2 种客观赋权思想，提出了一种基于熵权与变异系数组合赋权的复合评价指标。

首先，以RMSE 为例，给出熵权法定权的计算公式为

式中：σPRMSE和 µPRMSE分别为RMSE 的标准差和均值；σPr和 µPr分 别为平滑度的标准差和均值；CVPRMSE和CVPr分 别为RMSE 变异系数和平滑度变异系数；WPRMSE和 WPr分别为RMSE 和平滑度的权值。

得到上述2 种赋权方法所计算的权值后，为了弥补各自不足，最大限度地减少有用信息的损失，将熵权法与变异系数法相结合，构建组合赋权法，从而使指标的权值更加客观合理，得到最终权值，则有

在本文中，由于熵权法和变异系数法没有明确的可靠性比较，设为0.5 将组合赋权得到的RMSE 与平滑度的权值分别与归一化得到的RMSE 与平滑度值相乘并作和，得到复合评价指标 H，其表达式为

根据RMSE 与平滑度的定义及定权过程可知，随着分解层数的增加，复合评价指标 H将会出现一个极值，且这个极值为最小值，所对应的分解层数即为最优分解层数。

3 实验分析

3.1 仿真实验

为了能够准确比较验证本文所提出的复合评价指标在判断最优参数方面的有效性，采用第1 节真值已知的仿真信号进行分析。

分析时采用控制变量法，即在小波基不变的情况下，采用不同分解层数对含有噪声的信号进行处理，并选用不同的小波基分别对含噪信号进行处理。其他参数保持不变，阈值估计方法采用基于史坦的无偏似然估计原理（rigrsure）及软阈值处理函数。为验证方法的适用性，本文选取了文献[9]和文献[10] 2 种较为成熟的方法进行对比。

以sym4 小波基及db5 小波基为例，先计算多普勒信号在真值已知情况下（原始信号为无噪声的纯净信号）的RMSE 及SNR，再计算其在真值未知情况下（原始信号为加噪声的信号）的RMSE 与平滑度，并计算本文的复合评价指标 H、采用文献[9]的指标 T 和文献[10]的指标S，结果如表2 和表3 所示。

从表2 可以看出，选用sym4 小波基进行去噪处理时，在真值已知情况下，当分解层数为6 时，RMSE 最小，同时SNR 最大，说明最优分解层数为6；在真值未知情况下，随着分解层数的增加，RMSE不断增加，平滑度r 不断降低，这与前文判断一致，无法判断最优分解层数。根据复合评价指标 H，当分解层数为6 时出现最小值，说明最优分解层数为6，这与实际情况相符；文献[9]的指标 T也有类似的结论；而文献[10]的评价指标 S从第5 层开始变化率趋于平缓，判定最优分解层数为5，与实际情况不符，同时对于判断变化率是否趋于平缓具有一定程度的主观性。

表2 不同分解层数利用sym4 小波基处理的评价指标Table 2 Evaluation indexes of sym4 wavelet basis processing for different decomposition layers

从表3 可以看出，选用db5 小波基进行去噪处理时，在真值已知情况下最优分解层数为7，而在真值未知情况下，利用指标 H得到的最优分解层数为7，与实际情况相符；指标 T得到的最优分解层数为6，与实际情况不符；指标 S得到的最优分解层数为7，与实际情况相符。由此可以看到，复合评价指标H相比现有方法精度更高，具有更高的可信度。

表3 不同分解层数利用db5 小波基处理的评价指标Table 3 Evaluation indexes of db5 wavelet basis processing for different decomposition layers

为了更加全面地分析本文方法的可靠性，避免单一小波基函数对实验结果的误导，在真值未知情况下分别选择不同类型的小波基进行去噪分析，得到复合评价指标，从而判断最优分解层数，并以真值已知情况下得到的最优分解层数为参考，对比本文方法与现有方法，结果如表4 所示。

表4 不同小波基对应的最优分解层数Table 4 Number of optimal decomposition layers corresponding to different wavelet bases

从表4 可以得到，本文方法的正确率为80%，文献[9]和文献[10]所用方法的正确率分别为53%和47%，由此可看出，相比于现有方法，本文所提方法具有更高的准确率及可信度，而且可广泛应用于各种类型的小波基，是一种可靠的小波去噪质量评价方法。

3.2 实测惯性数据处理

为验证本文方法对惯性元件随机误差降噪处理的适用性，分别利用加拿大诺瓦泰公司SPAN-ISA-100C 型高精度光纤惯导和迈普时空研发的MPM39 型MEMS 惯性测量单元进行数据的采集。将2 款不同精度惯导设备安装在静态环境中，并预热30 min 后开始工作。为了使2 款设备的微小误差能够表现出来，需尽可能采集多的数据，为了达到光纤惯导采样时间，将2 款设备同样采集5 h 实验数据[20]，记录得到本次实验测试数据样本，采样频率设为200 Hz。

首先，利用Allan 方差分析误差信号的特点，Allan方差的最大特点就是能够对各种误差源进行单独辨识分析。2 款陀螺仪的误差分析结果如表5 和表6 所示。

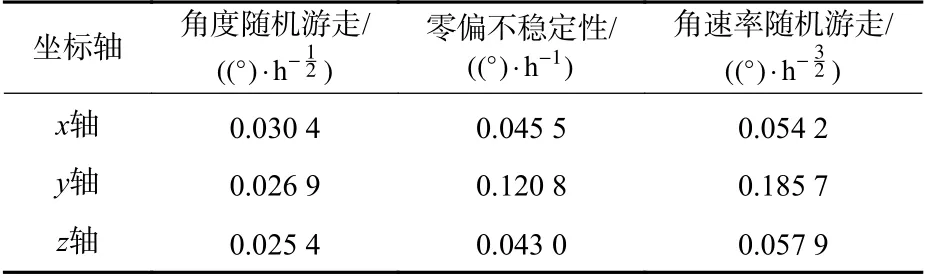
表5 SPAN-ISA-100C 陀螺仪Allan 方差分析结果Table 5 Allan variance analysis results of SPAN-ISA-100C gyroscope

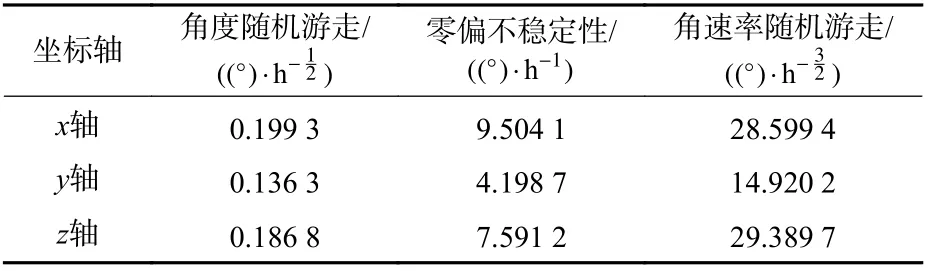
表6 MP-M39 陀螺仪Allan 方差分析结果Table 6 Allan variance analysis results of MP-M39 gyroscope

由表5 和表6 可知，陀螺仪的主要误差来自于角度随机游走、零偏不稳定性及角速率随机游走，随着陀螺精度的降低，3 轴各项误差源也随之变得不稳定，同时误差系数变大。

在小波去噪之前，确保其他参数一致，采用rigrsure 阈值选取准则、软阈值处理函数，选取不同的小波基函数，分解层数为2～10 层，采用控制变量法，选定sym6 小波基函数，分别利用本文复合评价指标 H 及文献[9]的指标 T进行最优分解层数的判定。2 款惯导设备的3 轴陀螺数据所对应的最优分解层数列于表7。其中，x1、y1、z1 分别表示SPAN-ISA-100C 陀螺仪的3 轴数据，x2、y2、z2 分别表示MP-M39 陀螺仪的3 轴数据。

在实验中同时发现,对于这2 款惯导设备共6 组数据，每组数据选取不同小波基函数得到的最优分解层数是相同的，SPAN-ISA-100C 的x 轴输出数据最优分解层数为4，其余数据得到的最优分解层数为5。由此，可以将对应最优分解层数设置为表7 中的分解层数，其他参数保持不变，根据复合评价指标 H判定最优小波基函数，得到对应最优小波基函数如表8 所示。

表7 陀螺数据对应的最优分解层数Table 7 Number of optimal decomposition layers corresponding to gyro data

表8 陀螺数据对应的最佳小波基函数Table 8 Optimal wavelet basis functions corresponding to gyro data

可知，复合评价指标 H可以将小波阈值去噪参数中的分解层数与小波基函数的选择统一起来，对SPAN-ISA-100C 的x 轴输出数据选用sym6 小波基函数，4 层分解层数；y 轴输出数据选用sym4 小波基函数，5 层分解层数；z 轴输出数据选用db8 小波基函数，5 层分解层数，取得最优的去噪效果。对MP-M39 的3 轴输出数据皆选用db7 小波基函数，5 层分解层数，取得最好的去噪效果。另外，对于不同的传感器所选择的最优参数往往不同，且对于同一传感器，由于其所处环境不同，所选用小波去噪参数亦不一致。基于经验所选择的参数缺乏理论指导，并不一定准确可靠。

同时，从表7 可以看出，利用2 种方法进行小波去噪时，SPAN-ISA-100C 的x 轴数据对应分解层数是相同的，但其他最优分解层数有所不同。为了直观判定2 种方法所得结果的准确性，以SPAN-ISA-100C 的y 轴输出为例，分别利用2 种方法得到降噪信号的时域曲线与频谱曲线，结果如图3 和图4所示。

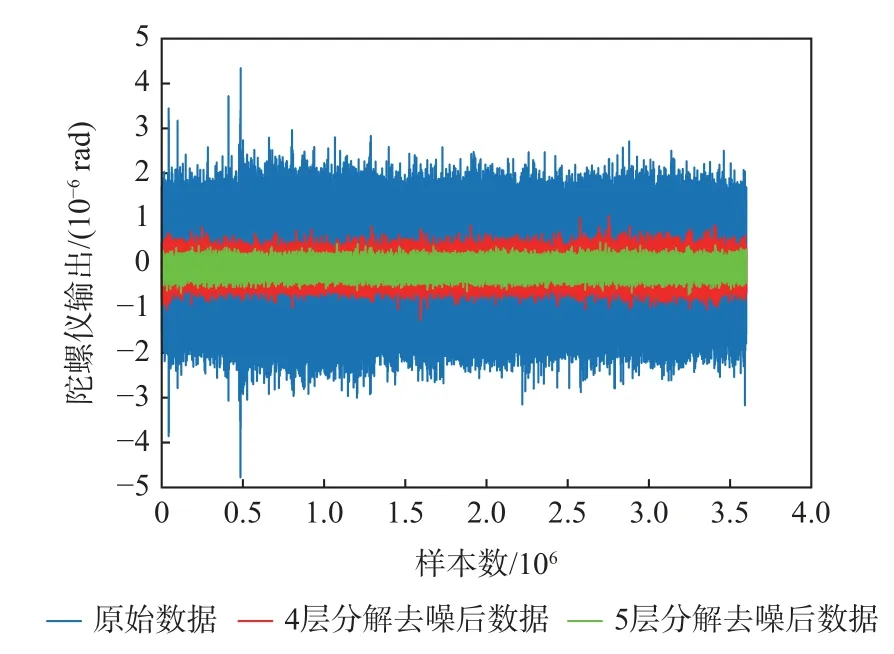
图3 原始信号与降噪信号时域曲线Fig.3 Time-domain curves of original signal and denoising signal

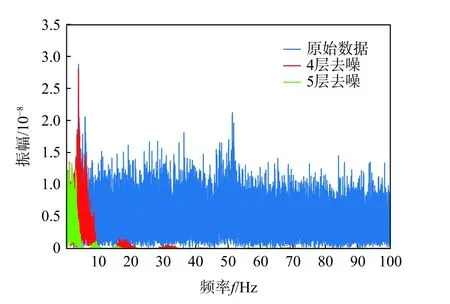
图4 原始信号与降噪信号频谱曲线Fig.4 Spectrum curves of original signal and denoising signal

图3 中，小波去噪后的信号都保留了原始信号的变化趋势，相比于4 层分解，5 层分解降噪信号峰值曲线更加光滑，波形图更加平稳，消除噪声更加彻底。图4 为信号的单边振幅谱图，去噪主要剔除高频无用细节信息，同时保留了低频有用近似信息，这也与小波去噪原理相符。5 层分解信号比4 层分解信号更有效地剔除了高频噪声，同时也说明5 层分解降噪信号的SNR 更高。由此可得，选取5 层分解降噪在此状态下效果最优，这也从另一个侧面说明了复合评价指标 H的有效性。

为了更加清晰地判断小波去噪效果，图5 给出了原始信号与分解层数为4 和5 的去噪信号的功率谱密度估计。可以看出，保留了低频有用信息，剔除了高频无用信息，同时，对中间的过渡信息适当进行了保留，相比于4 层分解降噪信号，5 层分解降噪信号剔除了较为微弱的噪声信号，也证明了5 层分解层数是最优分解层数。由于篇幅所限，本文不再分析其他输出数据去噪效果对比结果。

图5 原始信号与降噪信号功率谱密度图Fig.5 Power spectral density diagram of original signal and denoising signal

4 结 论

针对传统方法中经验模型缺乏理论依据的不足，本文提出了一种基于组合赋权法的小波去噪质量评价方法，得出以下结论：

1）通过实验发现，在真值未知情况下，单一评价指标无法指导小波阈值去噪过程中相关参数的选择，需构建更加全面的质量评价指标。

2）选取RMSE、平滑度2 个指标作为评价依据，对其进行初始化，通过引入信息熵权与变异系数2 种客观赋权法进行组合赋权，将归一化值与权值线性组合形成了一种新的小波去噪质量评价指标，并得出了相关计算公式。

3）通过对真值已知的模拟信号和真值未知的实测信号进行处理，证明该方法能够指导小波阈值去噪过程中相关参数的选择，具有更高的准确性与广泛适用性。