单目标概率约束规划的微种群免疫优化算法

李静，张仁崇，*，潘春燕，杨凯

(1.贵州商学院 计算机与信息工程学院，贵阳 550014；2.黔南民族师范学院 数学与统计学院，都匀 558000；3.贵州大学 贵州省大数据产业研究院，贵阳 550025)

在实际工程优化过程中，涌现出许多设计问题，如锌精矿混合成分[1]、第四方物流路径优化[2]、鲁棒动态调度[3-4]、电力系统故障诊断[5]、分布式微电网优化[6]、水资源管理[7]等，这些问题均被描述为单目标概率约束规划(single objective probabilistic constrained programming, SOPCP)，其模型主要有以下5个特征：①随机变量（噪声）一般呈复杂或未知分布；②目标函数在给定置信水平下由概率不等式确定；③约束条件至少含一个概率约束或一个机会约束；④随机函数通常是非线性、多模态或非凸；⑤决策变量通常在非凸区域取值。SOPCP 由于存在以上特征，导致其难以进行求解。因此，探讨出具有效率和效果突出、应用潜力高、抑噪能力强等优势的先进智能优化技术求解SOPCP，已成为亟待解决的技术难关。

在噪声处理方面，若噪声先验概率分布已知时，如噪声服从指数分布、正态分布、某些特殊非正态分布、均匀分布等，则凸性近似[8-9]、对数凹变换[10]、离散阶跃变换[11]等数学方法能转化部分SOPCP 为确定性解析模型，从而借助现有规划方法和静态智能算法求解，但由于模型转换复杂且需已知先验概率分布，致使它们在实际应用中受到很大限制。若噪声分布复杂或未知时，蒙特卡罗随机模拟因不受限噪声分布而被广泛用于SOPCP 的求解中。就其样本采样方法而言，重要采样[12]、拉丁超立方采样[12]均可处理机会约束，但此类方法实现较为困难且效率低下；静态采样、动态采样[13]、自适应采样[14-20]是处理机会约束和估计目标函数值的常用方法。静态采样要求所有个体都附加相同且足够大的样本量以获得近似解，尽管该方法简单，但会导致昂贵的计算资源消耗；动态采样要求个体依据其质量动态获取样本量，该方法样本总量小、效率高，但设计困难；自适应采样优于静态采样和动态采样，其要求个体自适应附加样本量，即质量越高的个体附加的样本量越大，反之则个体附加的样本量越小，这使得其在随机优化的背景下变得越来越流行。

从智能优化和工程应用角度来看，SOPCP 的研究成果依据算法类型主要分为3 类：遗传算法[1-3,5,7,21-22]、粒子群优化算法[6,23-27]和免疫优化算法[16-20,28]。遗传算法是在静态采样下求解SOPCP 问题的一种简单且实用的优化方法，其中个体的适应度通过随机模拟、模糊模拟、神经网络及同步扰动随机逼近等方法来估计，在工程优化设计中得到较好的应用，但其计算效率、求解质量和模型逼近还有待改进。例如，Liu[21]采用神经网络训练获取SOPCP 的近似模型，提出了几种适用于求解SOPCP 的改进混合遗传算法；卢福强等[2]构建了第四方物流路径优化的SOPCP 模型，引入移民算子增强种群多样性，且加入精英算子保存最优个体，从而获得改进型遗传算法求解。

粒子群优化算法具有结构简单、参数少、效率高等优点，在静态采样下与随机模拟、不确定函数模拟、神经网络结合已成为求解SOPCP 问题的替代方法，但该方法效率较低，解质量极大依赖于训练样本分布及规模，全局勘探能力不足。为克服此缺点，肖宁[23]将粒子的惯性权重设置为零，增强局部搜索能力，通过加入随机粒子丰富粒子群多样性。此外，粒子群优化算法已广泛应用于可描述为SOPCP 的工程优化问题[6,24-27]。

近年来，免疫优化算法被初步应用于求解SOPCP问题，且已有少量研究成果。在静态采样方面，段富等[28]利用随机模拟及神经网络逼近模型处理目标函数和机会约束概率值的估计问题，采用双变异和双克隆策略，提出改进的克隆选择算法求解。在自适应采样方面，张著洪等[16-17]针对一般类型的SOPCP问题，基于备受关注的危险理论，提出2 个具有自适应采样、繁殖、变异的微种群免疫优化算法求解，该方法效率较高，效果令人满意；同时，张著洪等[18-20]还针对单目标、多目标的概率优化问题分别设计了免疫优化算法求解，证明免疫优化算法求解此类问题具有良好潜力。

除上述算法外，部分其他启发式算法在静态采样下亦可有效求解SOPCP 问题，如量子进化算法[29]、帝国竞争算法[30]等。

综上所述，由于目标函数和约束条件存在随机变量，导致SOPCP 的求解一直是个难题。尽管一些智能算法在静态采样下能有效求解，但在效率和求解质量上的缺陷明显限制了其实际应用；虽然2 个自适应采样的微种群免疫优化算法[16-17]可高效求解SOPCP 问题，但其效率和寻优效果需进一步改善。因此，本文从生物免疫系统危险理论的免疫应答中获取灵感，探讨具有参数少、效率高、进化能力强、噪声抑制效果好、应用潜力高等优点的微种群免疫优化算法（micro immune optimization algorithm，µIOA-Ⅲ），同时提出目标值、机会约束的估计法分别高效估算目标值和机会约束的概率值。

本文µIOA-Ⅲ与µIOA[16]、µIOA-Ⅱ[17]借助危险理论启发和不同设计灵感，设计微种群免疫优化算法求解SOPCP 问题。其中，µIOA 是初次探讨问题求解的微种群免疫优化算法；µIOA-Ⅱ对µIOA 结构的复杂性和适应性进行改进，设计新变异策略提高解搜索能力，使用新的排序方法划分种群，将个体支配概念扩展到一般情况，引入个体生命周期模型防止劣质个体在进化过程中停留太久；在µIOA-Ⅱ的基础上，µIOA-Ⅲ构建新生命周期模型，基于此模型引入交叉算子加强群体内个体间信息交流，设计变异策略增加算法搜索能力，同时改进机会约束概率值的误差幅度和设计目标值的近似误差幅度，提出2 个新方法分别估计机会约束概率值和目标值。

1 问题描述与概率估计

1.1 问题描述

考虑如下SOPCP 问题:

其中：pˆi(x)为 pi(x)在 样本量ni(x)下的估计值；I{·}为指示函数，若条件为假则取0，反之取1；Δi(x)为改进的误差幅度，其设计如下：

式中：u(1+δ)/2表 示标准正态分布 的(1+δ)/2 分位数，δ ∈(0,1)；ψi(x) 为 pi(x)与 pˆi(x)的绝对误差幅度[14]，为更贴近真实误差幅度，被改进为 Δi(x)。一旦样本量ni(x)增大，则误差幅度 Δi(x)将变小，这有助于设计算法1 ，使个体自适应附加样本量高效获取估计值 pˆi(x)，并 给 出 经验约束 违 背 量 Γ(x)。若 Γ(x)=0，称x 为经验可信解，经算法2 可快速获得 x的经验目标值 fˆ(x)；反之，则称x 为经验非可信解。为有效比较候选解x 和y，引入如下经验支配概念[17]。

定义1 对于候选解 x,y ∈D，如果其满足下列4 个条件之一，则称x 经验支配y（简记 x ≺y）：

1)Γ(x)=0=Γ(y)∧fˆ(x)＜fˆ(y)。

2)Γ(x)=0 ＜Γ(y)。

3)0 ＜Γ(x)＜Γ(y)。

4)0 ＜Γ(x)=Γ(y)∧G(x)＜G(y)。

在以上4 个条件中，若x 和y 满足条件4)，此时可用G(x)和G(y)确定x 和y 的经验支配关系。

定义2 x*∈D称为SOPCP 问题的经验最优可信解，如果对于 ∀ x ∈D ，均有 x*≺x。

1.2 噪声处理

由于目标函数和约束函数存在分布未知或复杂的随机向量，SOPCP 问题极难或不能转化为解析模型，而随机模拟却是处理此类随机规划问题的有效工具。根据大数定律可知，样本量足够大时，机会约束的概率值和目标函数的估计值均逼近真实值，但不可避免会导致高计算复杂度；反之，每个候选解都附加一个小样本量，非可信解易被误认为是可信解，且优质和劣质的候选解难以辨别，使得优化质量严重受到噪声影响。为快速计算机会约束的概率值和目标函数的估计值，现提出以下2 种估计算法。

1.2.1 概率值估计

为快速有效地判定候选解x 是否经验可信，提出了机会约束概率值估计法。算法设计中，先计算确定约束的约束违背量 H(x)，在固定小样本量下快速初始估计所有机会约束的概率值 pˆi(x)。若x 不满足确定约束条件，则判定x 为非可信解；否则，借助误差幅度 Δi(x) ，自适应采样更新所有估计值 pˆi(x)，在较大样本量下使 pˆi(x)逼近真实值，依式(1)计算经验约束违背量 Γ(x)，判定x 是否为经验可信解。

算法1 机会约束概率值估计法。

同时更新 Δi(x) ，置 ni(x)←ni(x)+M。

步骤4.7 若i ＜ I，则i ←i +1，并转步骤4.2。

步骤4.8 若l ＜ I，则转步骤4.1；否则，转步骤5。

步骤5 置 δ ←δmin，依据式(3)重新计算误差幅度 Δi(x)，i=1, 2,···, I；依据式(1)计算经验约束违背量Γ (x)，并输出Γ (x)。

注：δmax和δmin选取较大值，δmax避免非可信个体因采样不足被误判为经验可信，且个体可信的概率至少为δmin。

在以上描述中，该算法的计算复杂度主要取决于步骤3 和步骤4，其在最坏情况下为O(ITmax+J+K)。步骤4 被设计自适应控制并赋予各机会约束不同样本量，使算法缩减样本总量并快速更新估计值 pˆi(x)；若x 不满足确定约束条件或不满足某个机会约束条件或明显满足所有机会约束条件，抑或是满足终止条件时，经步骤5 计算并输出 Γ(x)有效判定候选解x 经验可信性。此外，样本量 Tβi被设计与 βi有 关，若概率值 pi(x)与 置信水平 βi接近1（或0）时，则估计值 Δi(x)将非常小，极易使非可信解x 在式(1)下因采样不足被误判为经验可信解，此时x被要求在较大样本量 Tβi下 更新估计值 pˆi(x)。

1.2.2 目标值估计

为抑制噪声对目标函数的影响，提出目标值估计法。该算法在小样本量下，借助蒙特卡罗随机模拟，通过线性、加权、继承等方式强化噪声抑制效果，初始快速估计所有经验可信解x 的经验目标值fˆ(x)；在样本量上限Mn下，借助目标值近似误差幅度 Λ(x)辨析个体间优劣关系，并基于此设计自适应采样更新经验目标值 fˆ(x)，使 fˆ(x)逼近真实值。

算法2 目标值估计法。

步骤 1 输入参数：群体 Q={x1,x2,···,x|Q|}，置信水平 α，样本量m、Mn，参数δmax，m＜＜Mn。

步骤 2 置 m (xi)←m，δ ←δmax，i=1, 2,···, |Q|。

步骤 3 估计Q 中每个B 细胞x 的经验目标值。

步骤 3.1 令 s=m(x)；随机产生s 个样本向量ζk及其观测值 fˆs(x,ζk)(1≤ k ≤ s)，采用蒙特卡罗随机模拟估计B 细胞 x的 目标值 fˆs(x)。

步骤 3.3 借助数理统计[31]，将 Fˆ(x)- fˆ2(x)作为f¯(x)经 验目标值的近似偏差平方和，进而设计f¯(x)和 fˆ(x)的 误差幅度 Λ(x)如下：

步骤 4.5 i←i+1，若i ≤ |Q|，转步骤4.3。

步骤 4.6 若 j＜|Q|，转步骤4.1。

步骤 5 输出Q 中全体B 细胞 x的经验目标值fˆ(x)。

注：δmax选取较大值，利于设计算法自适应分配样本，并避免劣质个体在小样本下被误判为优质个体。

以上算法描述中，步骤3 经蒙特卡罗随机模拟和式(5)线性化初步抑制噪声获取估计值 fˆs(x)；再经式(6)继承、加权方式增强抑噪效果更新估计值fˆ(x)；设计 Fˆ(x)经式(7)继承、加权方式获得，进而设计目标值近似误差幅度 Λ(x)(见式(8))。步骤4 被设计使群体内所有个体循环依据经验目标值的误差幅度辨析其优势，并自适应附加样本量更新经验目标值；若个体与群内其他个体的目标值偏差较大使其易于辨析，其目标值可在小样本量下估计；反之，其目标值在较大样本量下估计。

2 危险理论与微种群免疫优化算法

2.1 危险理论

危险理论[32]是一种新流行的免疫学理论，与传统“自我-非我”模型区分异己的免疫理论应答机理不同。该理论认为，免疫应答启动仅取决于机体内受损、凋亡细胞（即感染细胞）释放的危险信号，对机体无害的内源、外源物质不作应答。具体而言，当机体内正常或生命力减弱的细胞非正常凋亡或因外源物质受损时，免疫系统发送信号1 给辅助性T 细胞，发送信号0 激活抗原呈递细胞（APC）释放信号2，辅助性T 细胞接收信号1、信号2 后被完全激活产生淋巴因子，促使机体发生免疫应答清理感染细胞，帮助机体恢复健康。免疫系统包括3 种细胞，即未感染、易感染和已感染细胞。

2.2 算法设计

以上危险理论的描述过程，为研究智能算法求解SOPCP 问题提供思路和灵感，µIOA-Ⅲ的运行机制如图1 所示。初始评价是经算法1 判定个体是否经验可信，在固定小样本量下经算法2 估计经验可信个体的目标值；群体分割是依据个体的经验约束违背量和经验目标值，将进化群分割成3 个子群：已感染、易感染和未感染子群。各子群个体依据其质量实施克隆变异，质量越高的个体繁殖克隆越多，且交叉概率、变异概率及变异幅度越小；同时，采用交叉算子加强各子群个体间的信息交流，促进协同进化，经变异产生多样、高质量的新个体。经初始评价后筛选优质的新个体，在较大样本量下与对应父代个体重新评价并比较，随机生成新个体替换进化已达生命周期的个体，产生新进化群体。

图1 µIOA-Ⅲ 的流程Fig.1 Flowchart of µIOA-Ⅲ

为便于算法的描述，结合以上SOPCP 问题和图1，将此问题视为危险信号，候选解视为B 细胞。基于此，µIOA-Ⅲ的描述如下。

算法3 µIOA-Ⅲ。

步骤 1 输入参数：样本量m、M，群体规模N，置信水平 α、βi，参数W，最大迭代数Gmax，m ≤ M，1≤ i ≤I。

步骤 2 初始化：置n←1，产生N 个随机B 细胞的初始群体 A={x1,x2,···,xN}，生存时间 w (xi)←0。

步骤 3 经验约束违背量：经算法1 估算群体A 中所有B 细胞 x的 经验约束违背量 Γ(x)。

步骤 4 经验目标值：Mn←(M+m)[2-cos(πn/Gmax)]；在小样本量 M1下经算法2 获取A 中所有经验可信B 细胞 x的经验目标值 fˆ(x)。

步骤 5 排序：借助定义1 的经验支配，优劣排序A中所有B 细胞，其中排在最前的B 细胞质量最好。

步骤 6 群体分割：A 中第1 个经验可信B 细胞视为已感染细胞构成子群B1，其余经验可信B 细胞视为易感染细胞构成子群B2；所有经验非可信B 细胞视为未感染细胞构成子群B3。

步骤 7 克隆：群体A 中第i 个B 细胞繁殖N-i+1个克隆。

步骤 8 交叉与变异。

步骤 8.1 交叉、变异概率：B 细胞 x的变异概率 pm(x)、交叉概率 pc(x)分别设计如下：

步骤 9 初始评价：Ci中每个B 细胞经算法1估算其经验约束违背量；Ci中经验可信B 细胞在小样本量M1下经算法2 估计其经验目标值，i =1,2,···,N。

步骤 10 重新评价并更新生存时间。

步骤 10.1 重新评价：xi与其对应子群Ci中最优B 细胞 zi构成优质子群Di；若Di中的2 个B 细胞均为经验可信B 细胞，需经算法2 在较大样本量Mn下重新估计经验目标值，i =1,2,···,N。

步骤 10.2 精英选择与更新生存时间：选择每个子群Di中最优B 细胞 yi构成群体E；其中，若Di的2 个B 细 胞 zi,xi满 足 zi≺xi，则 yi=zi，w(yi)←0；否则，yi=xi，w(yi)←w(xi)+1。经步骤5，优劣排序E 中所有B 细胞。

步骤 10.3 重置生存时间：若已感染B 细胞y1生存时间 w(y1)达 到生命周期W+N，重置 w(y1)←0；若易感染B 细胞 y2生 存时间 w(y2)达到生命周期W+N-1，重置 w(y2)←0；若易感染或未感染B 细胞yi生存时间 w (yi)达到生命周期W+N-i+1，则随机生成新B 细胞替换，经算法1 和算法2 初始评价新B 细胞，重置 w (yi)←0，i =3,4,···,N。

步骤 10.4 再次重新评价：若步骤10.3 随机生成新经验可信B 细胞，则群体E 中所有经验可信B 细胞经算法2 在较大样本量 Mn下重新估计经验目标值；经步骤5，优劣排序E 中所有B 细胞。

步骤 11 群体E 构成新进化群A；若Gmax≤n，则输出A 中最优质的B 细胞，结束；否则n←n+1，转步骤5。

在以上µIOA-Ⅲ算法描述中，步骤6 将群体A分割成3 类感染子群，经步骤7 使不同质量个体有差异繁殖克隆。步骤8 构建生命周期模型，基于此模型设计自适应的交叉与变异概率、变异分布指数；采用交叉算子促进群体间个体的信息交流，以及多项式变异、非均匀变异指导个体展开多方向进化，产生多样性丰富、质量高的子代个体。设计步骤10 筛选子代最优个体与对应父代个体，在较大样本量下更新经验目标值，有效辨析并挑选优质个体，随机产生新个体替换达到生命周期的劣质个体，获得多样性足够的新进化种群A。在设计中，进化个体仅1 次经算法1 估算其经验约束违背量，使远离约束边界的个体用小样本量估算，提高算法运行效率；边界可信邻域内的个体用较大样本量估算，使个体经验可信性不因采样不足被误判，利于搜索优质个体。

2.3 计算复杂度

经由以上µIOA-Ⅲ描述，其计算复杂度主要由步骤5、步骤8～步骤10 确定。步骤5 排序的计算复杂度为O(Nlog2N)；步骤7 至多克隆S=(N+1)N/2个，步骤8 执行交叉变异后的计算复杂度为O(pS)，步骤9 初始评价的计算复杂度为O(S(M12(log2M1+log2S)+ITmax+J+K))，步骤10 重新评价和排序的计算复杂度为O(NMn2log2Mn+ Nlog2N)。µIOA-Ⅲ在最坏情形下的计算复杂度为

由上述分析可知，µIOA-Ⅲ的计算复杂度由Mn、Tmax、N、p、I、J、K 确定，主要取决于 Tmax、Mn和N；Tmax和Mn主要依赖于样本量M，Mn随算法运行逐渐增大。因此，为使µIOA-Ⅲ高效率运行，M 和N 被要求取较小值。

3 数值实验

本文所有实验均在Windows XP 系统配置为CPU/2.20 GHz、RAM/1.99 GB 的Visual C++平台上进行。为分析µIOA-Ⅲ的算法性能，包括解质量、搜索效率和噪声抑制能力，选取代表性的、竞争性的智能优化算法SSGA-A[33]、SSGA-B[33]、FROFI[34]、C2oDE[35]、SPSO[23]、GA[21]、µIOA[16]及µIOA-Ⅱ[17]，在2 个理论测试问题、2 个工程问题上与µIOA-Ⅲ充分测试比较。以上算法具有相同的终止准则，即最大迭代次数为300。为降低随机因素对算法分析的影响，各算法对每个测试问题均独立运行100 次，输出的解需在样本量104下重新评价以使其经验约束违背量和经验目标值接近理论值；之后，将获取的结果用于统计分析。由于µIOA 和µIOA-Ⅱ具有自适应分配样本量能力，不需要为每个个体分配固定样本量；其余6 种比较算法的所有个体均附加相同样本量300[33]，其种群规模均设置为30；以上8 种比较算法的其他最佳参数设置均与原文献相同。

µIOA-Ⅲ的主要可调参数为种群规模N、样本量M、生命周期参数W。由于µIOA-Ⅲ是微种群优化算法，要求种群大小N 取较小的值(2～6 之间)[18,36]，特别是N=5 的小种群算法已有相关研究[18,36-38]。样本量M 直接影响算法搜索效果和效率，若取值过小，噪声抑制效果不理想，解质量受影响；相反，算法效率低。W 是控制个体生存时间的参数，若W很大，劣质个体将长时间停留；相反，获得一些有价值个体易消失，可取值在4～6 之间。经过实验测试后，设置N=5，m=2，M=10，W=5，δmin=0.99，δmax=0.99。

3.1 理论实验

问题1 多分布非线性概率优化问题[21]。

此问题常被用于测试算法的降噪能力、搜索效果[21,23,28,39]，其包含3 个连续决策变量 ( x1,x2,x3)，9 个服从均匀分布、正态分布或指数分布的随机变量；目标函数和2 个约束函数是非线性的且受3 种噪声影响，致使候选解 x是 否可信难以确定，目标值f¯(x)难以准确估计，问题求解难度极大。9 种算法独立求解此问题100 次的统计结果如表1 所示，目标值的箱线图和平均搜索曲线如图2 和图3 所示。表1中：min 为最小值，max 为最大值，mean 为平均值，St.Dev 为均方差，CI 为置信区间，IAE 为平均约束违背量，FR 为100 个最优解中经验可信解的比率，AR 为平均运行时间。图3 中，纵轴表示第n 次迭代时100 个最小经验目标值的平均值。

图2 问题1 的箱线图Fig.2 Box plots for problem 1

图3 问题1 的搜索曲线Fig.3 Search curves for problem 1

表1 问题1 的统计结果比较Table 1 Comparison of statistical results for problem 1

由表1 第7 列和第8 列可知，所有算法经100 次独立运行后都能找到可信解，其中，µIOA-Ⅲ、µIOA-Ⅱ和µIOA 在每次运行中均能找到可信解，C2oDE 次之，其他比较算法仅能找到部分可信解，且在某些次运行中有很小的约束违背量。表1 第2 列～第5 列显示，所有算法均获得相近的目标值，表现出稳定的搜索性能。但结合第7 列约束违背量，µIOA-Ⅲ、µIOA-Ⅱ、µIOA 寻到最优解是可信的，使其解质量相对较好；比较算法FROFI 有时难以寻到可信解，即使获得的目标值较大，其解的质量也相对较差。因此，从解质量的角度来看，µIOA-Ⅲ和µIOA-Ⅱ解质量最好，µIOA 次之且优于FROFI、C2oDE、SSGA-A、SGA-B，SPSO 较差。结合图2、图3及以上分析获知，µIOA-Ⅲ可快速、稳定求解上述问题，且解质量高。以上分析说明，9 种不同算法均能抑制噪声对解搜索的影响，主要原因归结为：①µIOA-Ⅲ、µIOA-Ⅱ和µIOA 针对约束条件、目标函数存在的噪声，分别设计相应的自适应采样策略抑制噪声；②其他比较算法在个体附加相同的固定大样本容量（300）下，可以控制噪声对算法寻优的影响。

此外，表1 第9 列清楚地说明µIOA-Ⅲ在执行效率方面优于其他比较算法，至少是SSGA-A 和SSGA-B的5 倍、FROFI 的12 倍、SPSO 的30 倍、C2oDE 和GA 的40 倍；尽管µIOA-Ⅱ和µIOA 也是快速的搜索算法，但效率不如µIOA-Ⅲ。

问题2 多模态概率约束优化问题。

此问题是通过修改高度非线性的多模态约束优化问题[39]而获得的，包含3 个连续决策变量(x1,x2,x3)，存在的7 个服从正态分布、均匀分布、指数分布或对数正态分布的随机变量，极大影响候选解可信性的判定和目标值的估计。此问题可用于测试算法是否有效抑制噪声，是否有效判定候选解可信性，以及全局搜索、跳出局部搜索的能力。与上述实验一样，每种算法直接求解该问题获得的统计结果如表2 所示，而对应的箱线图和平均搜索曲线分别如图4 和图5 所示。

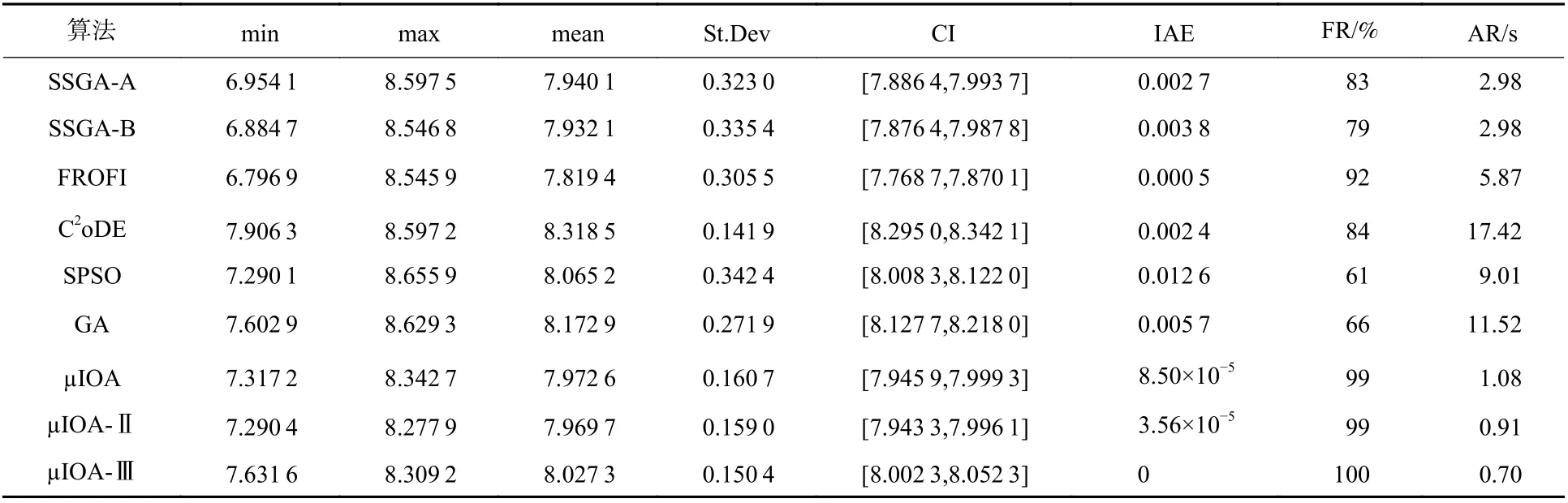
表2 问题2 的统计结果比较Table 2 Comparison of statistical results for problem 2

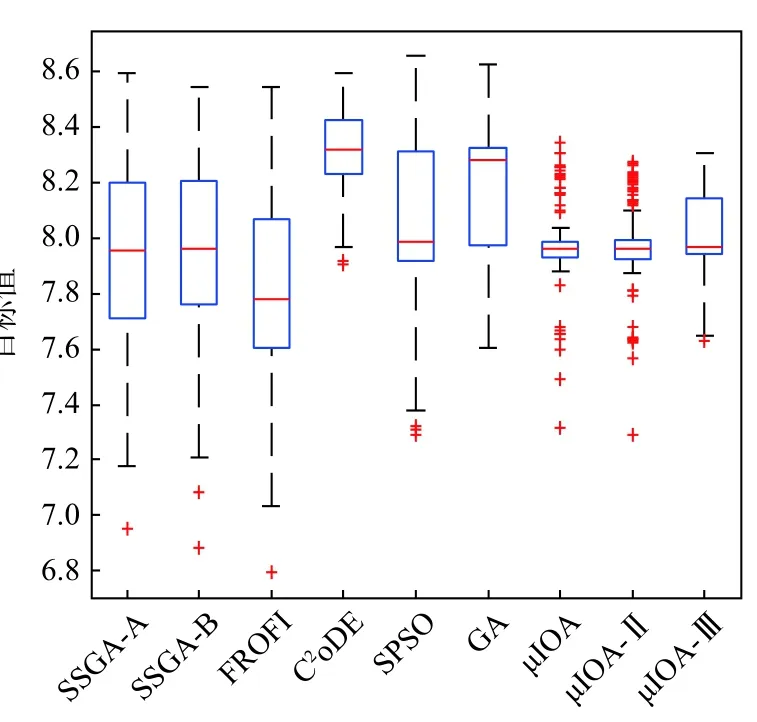
图4 问题2 的箱线图Fig.4 Box plots for problem 2

图5 问题2 的搜索曲线Fig.5 Search curves for problem 2

由表2 第7 列和第8 列获知，所有算法均能搜寻到可信解，其中µIOA-Ⅲ、µIOA-Ⅱ和µIOA 找到可信解的概率最高，但µIOA-Ⅱ、µIOA 有时难以找到可信解。同时，结合第4 列平均目标值可知，µIOA-Ⅲ、µIOA-Ⅱ和µIOA 获得满意的目标值；尽管C2oDE、GA、SPSO 的平均目标值占优，但其部分最优解不满足约束条件，使得解质量相对较差，因此噪声抑制、约束处理能力需要改进。结合第5 列均方差、第6 列置信区间及图4 表明，µIOA-Ⅲ和比较算法有相近的稳定性，但µIOA-Ⅲ和C2oDE 解搜索的稳定性最好。结合以上分析和图5 可知，µIOA-Ⅲ求解上述多模态概率约束优化问题，算法搜索稳定、收敛速度快且所获解质量高。

就平均运行时间而言，µIOA-Ⅲ的执行效率最高，µIOA-Ⅱ、µIOA 次之；µIOA-Ⅲ的效率至少是SSGA-A 和SSGA-B 的3 倍、FROFI 的7 倍、SPSO和GA 的11 倍、C2oDE 的23 倍。

3.2 工程应用

问题3 饲料混合成分问题。

此问题是通过修改原4 维饲料混合成分优化模型[33]获得的，饲料主要由大麦、燕麦、芝麻片、花生粉混合获得且所占比例为 x1、x2、x3、x4，原料中蛋白质含量百分比为随机变量 ξ1、ξ2、ξ3、ξ4，脂肪含量百分比为2.3、5.6、11.1、1.3，每吨原料成本为24.55、26.75、39.00、40.50 荷兰盾；在每吨饲料需求5%脂肪、21%蛋白质的条件下，构建以成本最小化为目标函数在噪声环境下求解。该问题存在5 个不同分布特征的随机变量，特别是噪声强度较大的 ξ3对解搜索的质量有很大影响，可以测试算法对含噪声的线性规划问题的应用能力。所有算法分别执行100 次求解此问题，统计结果如表3 所示，相应的箱线图和平均搜索曲线如图6 和图7所示。

表3 问题3 的统计结果比较Table 3 Comparison of statistical results for problem 3

图6 问题3 的箱线图Fig.6 Box plots for problem 3

图7 问题3 的搜索曲线Fig.7 Search curves for problem 3

经由表3 的IAE 和FR 值可知，µIOA-Ⅲ和µIOA-Ⅱ每次运行均找到可信解，µIOA 次之(99%)，C2oDE和SPSO 找到可信解的概率低且平均约束违背量略大，说明以上算法在寻找可信解的过程中，µIOA-Ⅲ、µIOA-Ⅱ和µIOA 能有效抑制噪声干扰，C2oDE 和SPSO 的搜索性能受噪声干扰大。经由IAE、FR、mean的值及图6 可知，µIOA-Ⅲ和C2oDE 的平均目标值最小，但C2oDE 因多数最优解违反约束条件获得较小的平均目标值最小，使得其解质量相对较差。为此，µIOA-Ⅲ求解上述问题获得的解质量优于其他算法。进一步，结合St.Dev、CI 的值及图7 表明，µIOA-Ⅲ和比较算法有相近的搜索效果和稳定性，但µIOA-Ⅲ相对更好，且具有良好的收敛性。

在执行效率方面，µIOA-Ⅲ、µIOA-Ⅱ、µIOA 的执行效率最高，SSGA-A 和SSGA-B 高于FROFI、SPSO、GA，C2oDE 效率最低。

问题4 混凝土泵车设计的费效权衡问题[40]。

为优化混凝土泵车设计，文献[40]选取底盘、臂架和泵送系统等重要部件中12 个关键设计参数，以泵车生命周期效能LCE 最大、费用LCC 最小构造目标函数获得SOPCP 问题。此问题包含4 个连续设计参数 (x1,x3,x4,x11)、8 个整型设计参数(x2,x5,···,x10,x12)，其中4 个整型设计参数和费用LCC 受方差较大的噪声影响，加之目标函数、约束函数是高度非线性，致使在大决策空间内寻求问题最优解变得极为困难，该问题可以测试算法对复杂噪声环境下工程问题的应用能力。实验与上述方式相同，各算法所得的统计结果如表4 所示，箱形图和平均搜索曲线分别如图8 和图9 所示。

表4 问题4 的统计结果比较Table 4 Comparison of statistical results for problem 4

图8 问题4 的箱线图Fig.8 Box plots for problem 4

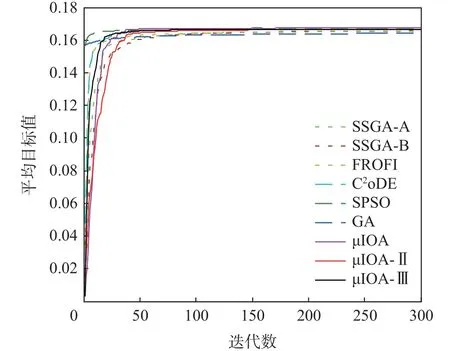
图9 问题4 的搜索曲线Fig.9 Search curves for problem 4

从表4 中IAE 和FR 值可以看出，所有算法在每次运行中都能找到可信解。由mean 值，所有算法所获最优的平均目标值之间存在微小差异，即解质量没有明显差异；但由图8 可看出，µIOA-Ⅲ、µIOA-Ⅱ、µIOA、C2oDE 及SPSO 的解质量最好且算法搜索更加稳定。进一步，由图9 表明，9 种算法求解该问题均是收敛的。

此外，效率是明显不同，由AR 值看出，µIOA-Ⅲ的效率最高，其效率稍优于µIOA-Ⅱ、µIOA，至少是其他算法的2.9 倍以上，而C2oDE、SPSO 和GA 需要更多的时间来寻找最优解。

3.3 灵敏度分析

µIOA-Ⅲ主要有3 个可调参数：N、M、W，选择多模态概率约束优化问题2 来测试算法的搜索性能是否在很大程度上依赖于它们参数的设置。为此，N、M、W 组成如表5 所示的7 种不同的参数组合，充分测试算法对参数设置的敏感性；算法在每种参数组合下独立运行100 次，得到的统计结果如表5 所示。

经由表5 可知，µIOA-Ⅲ在7 种参数组合下均独立运行100 次求解多模态概率约束优化问题，每次都能以很高的概率寻到满意的可信最优解，且解质量相近，表明算法µIOA-Ⅲ对参数N、M、W 的敏感度不高。在相同的迭代次数下，当生命周期参数W 增大时，局部搜索能力增强，解质量略微提高；当群体规模N、样本量M 增大时，解质量提高，效率降低；当样本量M 减小时，算法抑制噪声能力降低，使算法有时难以寻到可信解。为此，综合考虑算法的抑噪效果、寻优能力、运行效率，选取参数组合：N=5 , M=10, W=5。

表5 µIOA-Ⅲ在不同参数设置下求解问题2 的统计结果比较Table 5 Comparison of statistical results for solving problem 2 of µIA-Ⅲ in different parameter settings

4 结 论

单目标概率约束规划问题是一类具有综合工程应用背景的随机规划难题，为此，受生物免疫学中危险理论运行机制启发，设计了微种群免疫优化算法（µIOA-Ⅲ）求解。经理论分析和实验分析，得出以下结论：

1) 危险理论是探索智能优化算法求解SOPCP问题的一种有用的生物启发理论。

2) µIOA-Ⅲ的计算复杂度主要取决于群体规模、机会约束和目标函数的样本量上限。

3) µIOA-Ⅲ可以稳定、高效地搜索到满意质量的解，具有种群小、可调参数少、自适应性强等特点，是求解SOPCP 问题的一种有竞争力和应用潜力的优化算法。

4) µIOA-Ⅲ中机会约束概率值估计法能自适应为SOPCP 问题中各机会约束分配不同数量的样本，以有效抑制噪声干扰并估计概率值；目标值估计法能自适应为进化种群各个体分配不同数量的样本，以有效抑制噪声干扰并估算目标值。

5) µIOA-Ⅲ引入个体生命周期、交叉算子及自适应的交叉与变异概率、多项式变异、非均匀变异、分布指数等，可以有效增强算法进化能力。

此外，尽管该算法具有一些优异的性能，特别是其运行效率，但其工程应用仍需进一步研究。