基于烧失量试验的柔性石墨复合垫片极限温度应力水平确定*

陈春辉 胡思航 周剑锋 邵春雷

（南京工业大学机械与动力工程学院 江苏南京 211816）

柔性石墨材料具有高弹性、 耐腐蚀特性， 是一种性能优异的密封材料。 柔性石墨复合垫片的密封性能很大程度上取决于柔性石墨在复合板中的填充密度，但柔性石墨在高温下会与氧气反应造成质量损失从而引起性能劣化[1-3］。 研究高温条件下的柔性石墨复合垫片退化性能， 对于预测其密封性能具有重要意义。

加速退化试验可大大缩短试验时间， 提高试验效率， 国外学者对加速退化试验方法开展了大量研究。NELSON[4］总结了各种产品和材料的退化行为， 建立了加速退化试验模型。 ELSAYED[5］提出了加速退化试验分化模型， 将加速退化试验模型分为物理统计模型和数据统计模型两类。 SI 等[6］提出了具有长期退化记忆性质的加速退化试验模型， 弥补了传统模型忽略长期记忆进而导致有偏差的测试结果的缺陷。 LIM和YUM[7］提出了一种基于Wiener 过程的加速退化试验优化设计方法， 优化了加速应力水平与各应力水平下试样分配。 上述加速退化模型和方法为柔性石墨垫片的退化特性研究奠定了基础。 为进一步完善弹性垫片材料的质量评价方法， DERENNE、 MARCHAND等[8-9］对垫片（试验垫片含柔性石墨垫片） 进行了长时高温退化研究， 在考虑退化时间和温度对烧失量影响的情况下， 导出了烧失量和时间的关系参数Ap和当量时效停留参数Ae， 进而预测垫片的长期使用温度， 以保证垫片密封的可靠性和安全操作的使用条件。

本文作者将烧失量作为描述柔性石墨复合垫片的加速退化失效机制发生改变时的指标参数， 结合阿伦尼斯方程和幂律退化方程， 利用激活能相关理论[10］求得了失效机制未发生改变的温度应力水平区间， 然后根据威布尔分布参数与失效机制一致性的关系， 对处于临界点附近的温度应力水平下的失效机制进行了快速判别， 确定了极限温度应力水平， 从而为加速试验实施方案的确定奠定了基础。

1 加速退化试验

1.1 试验材料

试验对象为浙江国泰密封材料有限公司生产的柔性石墨复合垫片（DN32）。

1.2 仪器设备

试验用到的设备包括： （1） 恒温鼓风干燥箱，上海市实验仪器总厂； （2） 一体式马弗炉， 上海鳌珍仪器制造有限公司； （3） 电子天平， 上海衡平仪器仪表厂（精度0.01 g）。

1.3 预处理

使用蒸馏水清洗试样10 min， 冲刷掉试样表面灰尘， 然后将试样浸入无水乙醇溶液中静置5 min， 去除试样表面油污， 用镊子夹出试样置于空气中晾晒，然后将其放入干燥箱中烘1h， 取出冷却至室温后备用。

1.4 烧失量测定

柔性石墨复合垫片烧失量的测定按照国家标准[11］进行。 对干燥后的试样进行称重， 同时升高马弗炉的炉温， 待温度稳定在预定温度后放入试样， 灼烧一定时间， 冷却至室温后称重。 烧失量的计算公式如下：

式中：m1为灼烧前的试样质量；m2为灼烧后的试样质量；w为烧失量。

2 试验结果与讨论

2.1 基于激活能不变的失效机制一致性检验

文献[12］汇总了柔性石墨的一些经验定律， 并首次使用幂律方程描述了柔性石墨的相关物理性能，并严格推导了幂律的指数。 因此， 在这样的基础上，推断烧失量与时间可能也存在这样的幂律关系， 于是文中使用幂律退化模型[13］作为柔性石墨复合垫片的烧失量退化模型。

对于幂律退化轨道， 在退化时间t时刻的烧失量为

式中：β是退化率因子；β1是退化曲线的形状参数。

上式可改写为

式中：K是退化速度常数，

参考文献[14-15］， 选取温度应力范围为773 ～923 K， 每隔50 K 选取一个温度应力水平进行试验，得到如表1 所示的退化数据。

表1 不同温度下柔性石墨复合垫片加速退化数据Table 1 Accelerated degradation data of flexible graphite composite gaskets under different temperature

通过计算可求得不同温度应力水平下的退化模型参数， 进而可绘制成如图1 所示的加速退化曲线。

图1 加速退化模型拟合曲线Fig.1 Fitting curves of accelerated degradation model

退化模型拟合后获得的拟合指标参量值如表2 所示。 观察表2， 残差平方和（SSE） 比较接近0， 均方根误差（RMSE） 接近0， 确定系数（R-square）接近1， 可以说明幂律退化模型具有较好的拟合效果， 数据预测较为接近实际情况。

表2 不同温度应力水平下的拟合指标参量值Table 2 Parameter values of fitting index under different temperature stress levels

根据Arrhenius 方程， 退化速度常数K与开氏温度T之间的关系为

式中：A是阿伦尼乌斯常数；E是激活能；R是摩尔气体常数。

对式（4） 进行对数变换， 可得：

式中： 激活能E是lnK和1／（RT） 的一次函数的斜率， 故激活能Ei为

根据Arrhenius 模型理论， 处于同一失效机制下的激活能相同， 因此， 若在加速过程中激活能发生变化， 也就意味着失效机制发生了改变。

建立lnK和1／（RT）的关系， 如图2 所示。

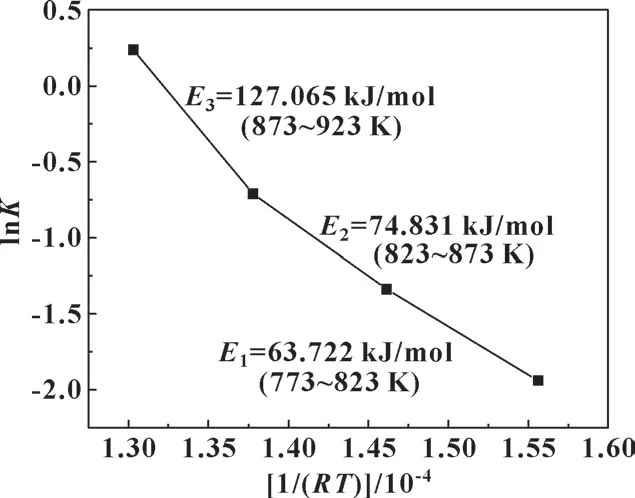
图2 不同温度应力水平区间下的激活能Fig.2 Activation energy at different temperature stress levels

由图2 可知， 温度处于823～873 K 区间的激活能与温度处于773 ～823 K 区间的激活能相比发生了较大的变化， 说明在介于823 ～873 K 之间的某个温度点上， 加速退化失效机制发生了变化。 根据文献[14］， 石墨垫片在723 K 的温度条件下经历500 h 的灼烧后质量损失几乎未发生变化， 故文中不考虑温度处于723～773 K 区间的激活能。

2.2 基于威布尔分布的失效机制一致性检验

已知柔性石墨复合垫片加速退化失效机制改变发生在823～873 K 之间， 且威布尔分布的形状参数反映了失效机制， 因773 K 是垫片的最高使用温度， 故将该温度应力水平设置为参照组， 和823 K 下获得的失效数据的形状参数进行比对。

选取773 和823 K 2 个温度应力水平继续开展加速退化试验， 每个温度应力水平使用4 个垫片， 共8个垫片。 在加速退化试验的过程中， 取烧失量为5%时的退化时间为失效时间（通过退化模型可得）， 进而可获得柔性石墨复合垫片在2 种温度应力水平下的伪失效数据。

温度应力水平773 K 下的垫片加速退化曲线如图3 所示， 该温度应力水平下的4 个试样的退化曲线都是增函数， 故是增长退化曲线， 该增长退化曲线呈上凹状， 增长退化先快后慢， 又称凹退化。 温度应力水平823 K 下的垫片加速退化曲线如图4 所示， 该温度应力水平下的4 个试样的退化曲线也为增长退化曲线， 该曲线的增长退化情况为先慢后快， 又称凸退化。

图3 柔性石墨复合垫片加速退化曲线（773 K）Fig.3 Accelerated degradation curves of flexible graphite composite gaskets （773 K）： （a） specimen 1；（b） specimen 2； （c） specimen 3； （d） specimen 4

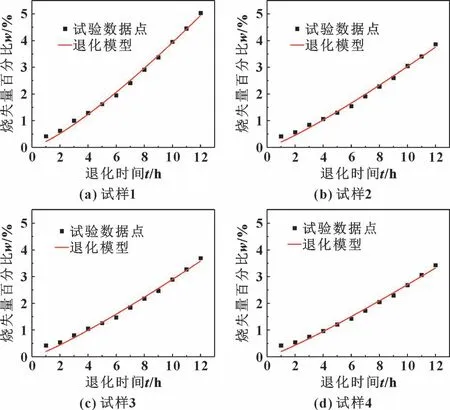
图4 柔性石墨复合垫片加速退化曲线（823 K）Fig.4 Accelerated degradation curves of flexible graphite composite gaskets （823 K）： （a） specimen 1；（b） specimen 2； （c） specimen 3； （d） specimen 4

获得的伪失效数据如表3 所示。

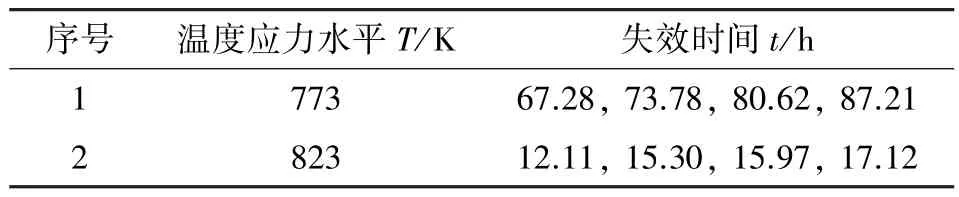
表3 柔性石墨复合垫片伪失效数据Table 3 Pseudo failure data of flexible graphite composite gaskets

威布尔分布由Weibull 依照最弱环和串联理论提出， 这一理论认为整体中任何一个部位的失效即可认为整体失效。 威布尔分布具有广泛的适应性， 因某一局部失效而导致全局停止运行的元件设备等都可以视为服从威布尔分布[16］。 参考文献[17］， 假设柔性石墨复合垫片的伪失效数据服从威布尔分布， 即

式中：t为退化时间；m为形状参数，m＞0；η为尺度参数，η＞0。

采用F检验法对伪失效数据的分布特征进行分析。 为验证伪失效数据服从威布尔分布的假设， 假设

式中：m、η未知。 为检验假设， 选取n个试样进行试验， 到r个试样失效时停止试验， 可得失效时间

对检验统计量进行估计的同时可设定显著性水平α， 并依据式（10） — （12） 计算各统计量。

在原假设H0成立的情况下， 近似服从自由度为2（r - r1-1） 和2r1的F分布， 故检验的拒绝域为

以温度应力水平为773 K 的伪失效数据为例， 对 其进行F检验， 检验所需的参量如表4 所示。

表4 F 检验的参量值（773 K）Table 4 Parameters for F test （773 K）

此时W的观察值为1.117。 取显著性水平α＝0.05， 查F分布表可得检验临界值F0.975（2， 4） ＝10.650，F0.025（2， 4） ＝0.094， 因F0.025（2， 4） ＜W＜F0.975（2， 4）， 故不拒绝假设H0， 即认为在温度应力水平773 K 下的伪失效数据服从威布尔分布。

以温度应力水平为823 K 的伪失效数据为例， 对其进行F检验， 检验所需的参量如表5 所示。

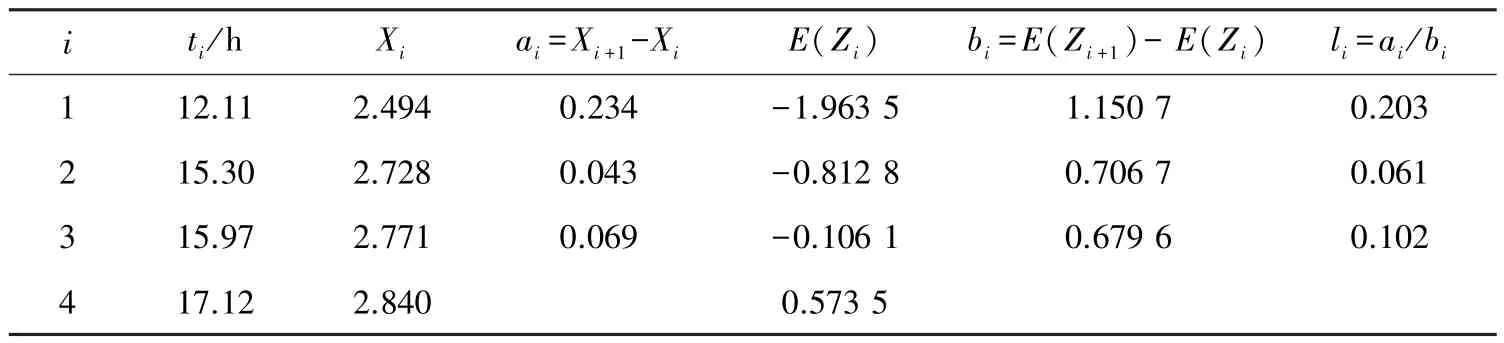
表5 F 检验的参量值（823 K）Table 5 Parameters for F test （823 K）

此时W的观察值为0.773。 同理可得， 在温度应力水平823 K 下的伪失效数据服从威布尔分布。

在伪失效数据服从威布尔分布的情况下， 可采用最佳线性无偏估计（BLUE） 计算相应的威布尔分布参数的估计值。 通过查表可获得系数D（n，r，i） 和C（n，r，i） ， 且μ的估计值＾μ和σ的估计值＾σ与其的关系为

以温度应力水平为773 K 的伪失效数据为例， 最佳线性无偏估计计算所需参量如表6 所示， 并按照式（14） 计算， 可求得则相应的威布尔分布参数的估计值

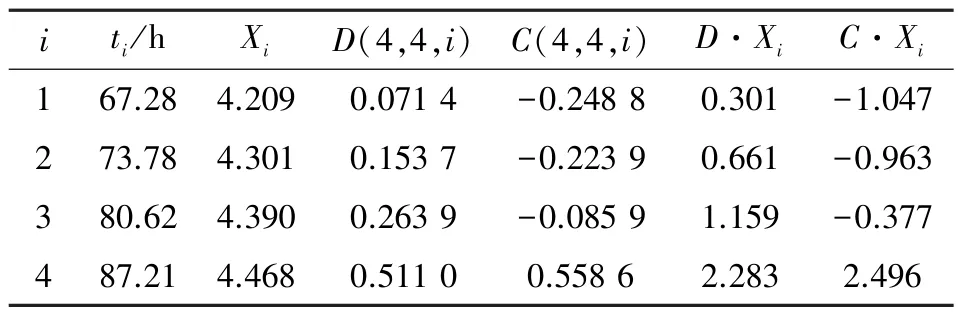
表6 BLUE 参量（773 K）Table 6 Parameter of BLUE （773 K）

以温度应力水平为823 K 的伪失效数据为例， 最佳线性无偏估计计算所需参量如表7 所示， 并按照式（14） 计算， 可求得则相应的威布尔分布参数的估计值

表7 BLUE 参量（823 K）Table 7 Parameter of BLUE （823 K）

现要检验2 个不同温度应力水平下的失效机制是否一致， 即检验两者的形状参数是否一致， 即检验假设H0：m1＝m2，H1：m1≠m2。 利用形状参数m的估计值可计算检验统计量F的观察值为1.064。 在给定显著性水平α＝0.05 的条件下， 查表获得相应的参量查F分布表可得检验临界值F0.975（9， 9）＝4.030，F0.025（9， 9）＝0.248， 因F0.025（9， 9）＜F＜F0.975（9， 9）， 检验统计量F的观察值未落入拒绝域中， 故不拒绝假设H0， 即认为在2 种温度应力水平下柔性石墨复合垫片失效机制并未发生变化。

3 结论

（1） 从拟合指标来看， 幂律退化模型较好符合柔性石墨复合垫片的退化轨道， 可以较好地预测退化量。

（2） 利用基于Arrhenius 模型的激活能理论确定了柔性石墨复合垫片失效机制发生变化的温度区间是823～873 K。

（3） 结合威布尔分布模型， 利用加速失效机制一致性与形状参数的关系， 初步确定了柔性石墨复合垫片的极限温度应力水平为823 K。