盾构机主驱动VD 形密封圈密封性能研究与优化*

张青雷 朱洪秀

（上海海事大学物流工程学院 上海 201306）

隧道掘进机的刀盘驱动密封圈作为盾构机的核心部件， 对掘进机的工作效率有着决定性的影响， 同时也是隧道掘进机驱动系统产生故障的突出因素。 近年来， 随着我国自主设备研究水平的逐渐提升， 在驱动刀盘密封圈的研究与设计上获得了突破性的进展， 打破了国外技术垄断和封锁。 但是， 在实际应用和操作过程中发现盾构机驱动刀盘驱动密封圈仍然存在故障。 同时随着隧道盾构机应用的不断发展， 其应用场合不断多样化， 在越江隧道、 饮水工程、 采煤工程方面也得到广泛运用。 为了保证盾构机组内人员以及设备安全， 盾构机的密封性能要求也越来越严格。 刀盘驱动密封的主要功能是确保盾构机的刀盘驱动正常工作， 其工作原理是通过安装与布置密封圈， 利用密封圈的压缩变形产生的挤压应力来抵抗外部水压， 防止地下水从刀盘驱动与盾构机箱体配合面之间的空隙向机组内部泄漏。

为了保证刀盘驱动密封圈设计的安全性和经济性， 常采用有限元分析方法对其展开研究。 关于橡胶密封圈的有限元分析与本构模型研究发展趋于完善，包括Neo-Hookean model、 Mooney-Rivlin model、 Yeoh model 和Ogden model 等橡胶本构模型理论[1-2］。 其中Mooney-Rivlin 模型符合小应变或中等应变（100%拉伸应变； 30%的压缩应变）， 根据阶数高低， 常见的Mooney-Rivlin 模型有二参数、 三参数、 五参数、 九参数形式。 参数形式越高， 本构模型越能精准模拟更加复杂的橡胶应力应变曲线， 但其代价是本构模型参数的拟合可能更加困难， 以及更多的计算量和更难收敛[3］。 为了简化计算量文中采用通用的二参数Mooney-Rivlin 模型[4-6］。

众多学者已开展了橡胶材料的密封性能以及防渗透研究。 李海宁等[7］通过ANSYS 有限元软件研究了氢化丁腈橡胶和三元乙丙橡胶的C 形组合密封的密封性能， 研究了不同密封弧面半径对组合形密封接触应力的影响。 郭媛等人[8］利用ANSYS 有限元软件研究了格莱圈在不同预压缩率、 不同滑块厚度以及不同硬度下的O 形圈材料的动密封性能。 周文锋等[9］采用Mooney-Rivlin 二参数模型， 分析研究了不同接触应力对应渗漏临界水压的关系， 并通过曲线拟合得出“T 字缝” 渗漏临界水压公式。 同时学者们对盾构机橡胶密封圈的研究也取得了一定的进展。 刘杰夫和吕晓仁[10］研究了泥水盾构机O 形密封圈的接触应力与压缩率、 流体压力、 摩擦因数和硬度之间的关系， 发现摩擦因素对密封圈接触应力的影响较小， 其余参数对密封圈接触应力的影响显著。 张中华等[11］研究了VD 密封圈前后不同压差对密封性能的影响， 从而构建了合适的背压来提高密封系统整体的承压能力， 同时优化了现有的安装结构以进一步提高密封的可靠性。

为研究盾构机主驱动密封圈压缩量以及正反面润滑油脂载荷对密封圈密封性能的影响， 本文作者研究不同压缩量下VD 形密封圈的密封性能的变化规律，探究相同压差及不同正反面介质压力下密封圈密封性能的稳定性； 同时利用响应曲面法优化刀盘VD 形橡胶密封圈的装配结构， 通过结构改变实现VD 形密封圈接触压力的参数可调， 实现最优的设计密封工况。

1 有限元模型建立

刀盘掘进机密封主要起到防止外部泥浆的渗漏，提取如图1 所示的VD 密封结构的有限元分析模型，VD 密封结构主要由密封压条、 配合面和VD 密封圈组成。 图中， 在配合面与VD 密封圈底部的相对位置模拟了安装时的压缩量d， 通过改变d的数值、 正反加载面的压力模拟工作时液体压力的作用， 其中泥浆压力或前一级的润滑油脂压力施加在密封圈正面加载面， 反面加载面则施加略低的润滑油脂压力。 同时为了模拟橡胶圈安装时存在一定的预紧力， 通过控制密封压条的位移Δd来实现。 在Ansys 的瞬态动力学模块中定义密封压条和配合面的材料属性为结构钢， 以及VD 密封圈的丁腈橡胶 （NBR） 材料为两参数Mooney-Rivlin 模型， 同时分析时开启大变形。

图1 VD 形密封圈有限元分析平面Fig.1 Finite element analysis plan of VD sealing ring

1.1 橡胶材料本构模型

两参数Mooney-Rivlin 模型的参数拟合有经验法、硬度拟合以及实验拟合等方法[12-15］。 橡胶类材料的Mooney-Rivlin 两参数本构方程可以很好地模拟其力学行为， 公式如下：

式中：I1、I2为应变张量的2 个主不变量；C10、C01为材料常数；d为材料的不可压缩系数；J为弹性变形梯度的行列式。

文中本构参数的获得通过经验法估算获得， 橡胶硬度Ha与弹性模量E（MPa） 的关系式为

可求得NBR 硬度为Shore 85 时， 对应的两参数Mooney-Rivlin 模型的参数C10＝1.76 MPa，C01＝0.44 MPa。

不可压缩系数d为

其中μ＝0.499。

为了保证橡胶材料求解时能有良好的收敛， 对于两参数的Mooney-Rivlin 模型的参数需满足下列的正定性要求：

1.2 有限元模型参数以及边界条件

图1 所示为刀盘掘进机所用的VD 密封结构计算模型，d为密封圈的压缩量， Δd为密封圈安装时的预紧量。 橡胶材料密度1 250 kg／m3， 其两参数的Mooney-Rivlin 模型的参数C10＝1.76 MPa，C01 ＝0.44 MPa，d＝0.000 91 MPa-1。 除了密封圈， 其余结构为结构钢， 其密度7 850 kg／m3， 弹性模量为200 GPa，泊松比为0.3。

文中分析时， 设计压缩量分别为3、 4、 5、 6、 7 mm， 密封圈正面-反面加载力分别为0-0、 0.3-0、0.6-0.3、 0.9-0.6 MPa。

在有限元软件中通过修改相应的参数， 用d来控制压缩量以及改变VD 密封圈的正反加载面压力， 来研究其密封性能与压缩量和密封圈正反加载面压力之间的联系。 在接触设置中设为摩擦接触， 润滑条件下滑动摩擦因数设为0.1， 静摩擦因数设为0.2。 故设立VD 形密封圈与配合面的接触摩擦因数为0.1， 与压条的接触摩擦因数为0.2。 为使模型易于收敛， 允许模型存在轻微的穿透， 选用Augmented-Largrange接触。

采用有限元分析VD 形密封圈密封工况时， 通过改变配合面的直径使密封圈有不同的压缩量， 然后对其进行安装配合和施加介质压力。 密封圈具体载荷步施加过程如下：

（1） 通过对配合面施加X方向上的位移来改变压缩量， 同时设置密封压条的位移参数Δd， 实现密封圈安装时预紧力；

（2） 控制配合面Y方向的位移， 来模拟密封圈无介质压力时的安装过程；

（3） 对密封圈正面-反面加载面施加介质压力，模拟密封圈工作时受到介质润滑油脂的压力作用。

2 密封参数对密封性能的影响

密封圈与驱动旋转装置配合面之间的性能， 受到压缩量以及工作压力的影响， 通过研究它们之间的关系， 以提高密封性能的可靠性， 可为动态分析以及热分析等提供理论基础。

2.1 压缩量对密封性能的影响

图2 所示为正反面油压0.9-0.6 MPa 下不同压缩量时的VD 形密封圈von Mises 应力云图。 结果显示，不同压缩量时VD 形密封圈的应力集中主要位于2 个部位： VD 形密封圈齿形根部和齿形顶部接触区域。对比压缩量为7 mm 时， 正反面加载压力分别为0.9-0.6 MPa 和0-0 MPa 下的应力云图， 如图3 所示， 可以发现配合面的压缩量是密封圈齿形根部产生弯曲应力集中的主要原因； 同时润滑油脂的压力作用， 使其根部应力集中的区域产生了偏移， 并导致根部的拉应力明显加剧。 齿形顶部接触区域存在的应力集中， 主要是由于润滑油脂压力的加载， 导致其接触面附近的赫兹接触应力显著增大； 同时接触面的应力值大小影响接触面密封性能。

图2 不同压缩量下von Mises 应力云图（MPa） （密封圈正反面油压0.9-0.6 MPa）Fig.2 Nephogram of von Mises stress at different compression amount （MPa） （oil pressure of 0.9-0.6 MPa on both sides of sealing ring）： （a） compression amount of 3 mm； （b） compression amount of 4 mm； （c） compression amount of 5 mm； （d） compression amount of 6 mm； （e） compression amount of 7 mm

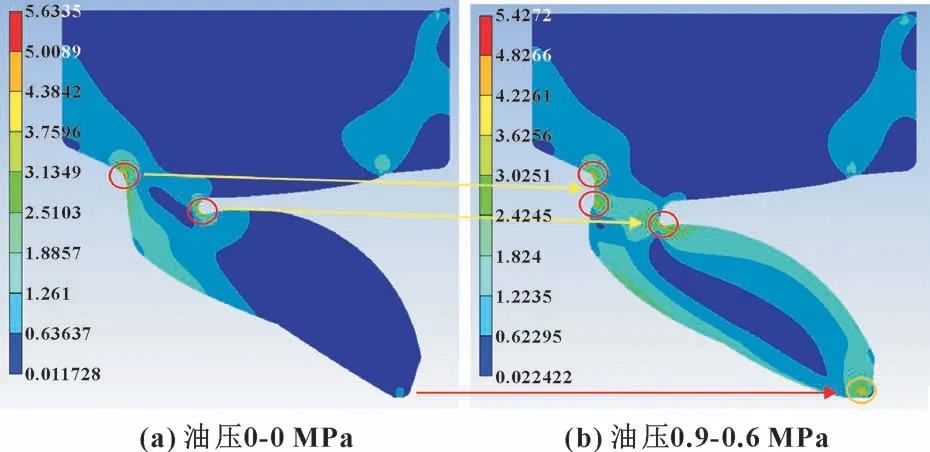
图3 压缩量为7 mm 时不同正反面油压下的von Mises 应力对比（MPa）Fig.3 Comparison of von Mises stress at 7 mm compression amount under different oil pressure （MPa）： （a） oil pressure of 0-0 MPa； （b） oil pressure of 0.9-0.6 MPa

VD 形密封圈最大许用应力值远大于文中分析得到的其最大应力， 但由于密封圈与接触面处于滑动配合状态下， 对其密封性能有更高的要求； 接触应力与转速影响密封圈工作时的磨损与热疲劳， 所以控制密封圈接触面的应力与接触压力就显得极其重要。 图4示出了不同密封圈压缩量与接触面处的von Mises 应力的关系。 可见， 在正反面载荷工况为0.9-0.6 MPa时， 其接触面的最大von Mises 应力随着压缩量的增加先不断上升然后逐渐趋于稳定。 这是因为压缩量越大， 会导致接触面积越大， 从而缓解接触面的最大von Mises 应力的增幅。

图4 von Mises 应力随压缩量的变化（正反面油压0.9-0.6 MPa）Fig.4 Variation of von Mises stress with compression amount （oil pressure of 0.9-0.6 MPa on both sides of sealing ring）

图5 所示为在正反面载荷工况0.9-0.6 MPa 下，不同压缩量下VD 形密封圈接触面最大接触应力云图， 图6 示出了最大接触应力随压缩量的变化关系。在相同的正反面加载压力下， 随着压缩量的不断增加， 其接触面面积也不断增加， 因而接触面的最大接触压力不断下降。

图5 不同压缩量下最大接触应力云图（MPa） （正反面油压0.9-0.6 MPa）Fig.5 Nephogram of the maximum contact stress under different compression amount （MPa） （oil pressure of 0.9-0.6 MPa on both sides of sealing ring）： （a） compression amount of 3 mm； （b） compression amount of 4 mm； （c） compression amount of 5 mm； （d） compression amount of 6 mm； （e） compression amount of 7 mm

图6 最大接触应力随压缩量的变化（正反面油压0.9-0.6 MPa）Fig.6 Variation of maximum contact stress with compression amount （oil pressure of 0.9-0.6 MPa on both sides of sealing ring）

2.2 正-反加载面介质压力对密封性能的影响

图7 所示为压缩量为7 mm 时， 不同正-反加载面介质压力工况下VD 形密封圈von Mises 应力云图。VD 形密封圈的应力集中主要由安装时的预安装量和压缩量所决定， 而接触面的接触应力与正反面加载压力有关， 其接触面的von Mises 应力随着正反面压力的提高而呈现显著上升的趋势， 图8 示出了不同正反面加载工况下的von Mises 应力分布。 可以看出， 接触面的von Mises 应力在存在压差时显著增大； 而在正反面压差不变的情况下， 其接触面von Mises 应力随着正反面施加压力的增加而增加， 但增加幅值较小。 这表明在压差一定的情况下， 正反面施加的压力增加对于VD 形密封圈接触面的von Mises 应力影响 较小， 但压差变化对于其影响较为显著。

图7 不同密封面正反面加载工况下von Mises 应力云图（MPa） （压缩量7 mm）Fig.7 Nephogram of von Mises stress under different load conditions on both sides of sealing ring （MPa） （compression amount 7 mm）： （a） 0-0 MPa； （b） 0.3-0 MPa； （c） 0.6-0.3 MPa； （d） 0.9-0.6 MPa

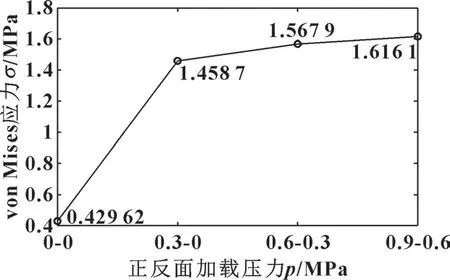
图8 不同密封面正反面加载工况下von Mises应力分布（压缩量7 mm）Fig.8 Distribution of von Mises stress under different load conditions on both sides of sealing ring（compression amount 7 mm）

图9 所示为压缩量为7 mm 时， 不同正-反加载面介质压力工况下VD 形密封圈最大接触应力云图。接触面最大接触压力与正反面加载压力的关系与上述von Mises 应力变化规律相似， 压差变化对接触面的压力影响较大， 而压差相同时， 正反面压力的升高也会导致其接触面最大接触压力的上升。 如图10 所示，当正面压力以0.3 MPa 增幅增加时， 其接触面最大接触压力的增幅分别为0.280 8、 0.357 9 MPa。 说明随着正面压力升高， 该VD 形密封圈接触面最大压力也保持相近幅值的上升。 该密封圈结构设计保证了密封接触压力的裕度， 从而保证密封结构密封效果的稳定性。

图9 不同密封面正反面加载工况下最大接触应力云图（MPa） （压缩量7 mm）Fig.9 Nephogram of maximum contact stress under different load conditions on both sides of sealing ring （MPa）（compression amount 7 mm）： （a） 0-0 MPa； （b） 0.3-0 MPa； （c） 0.6-0.3 MPa； （d） 0.9-0.6 MPa

图10 不同密封面正反面加载工况下最大接触应力分布（压缩量7 mm）Fig.10 Distribution of maximum contact stress under different load conditions on both sides of sealing ring （compression amount 7 mm）

2.3 压缩量和正-反加载面介质压力对密封性能的影响

图11 示出了不同压缩量下， 密封圈接触面von Mises 应力和最大接触应力随正-反加载面加载压力的变化关系。

如图11 （a） 所示， 随着密封圈压缩量的增加，VD 形密封圈接触面的最大von Mises 应力总体呈现出增大趋势， 且在相同压缩量下最大von Mises 随密封圈正反面加载压力的变化规律均相似。 如图11 （b）所示， 随着压缩量的不断增加， VD 形密封圈接触面的最大接触压力总体呈现出下降趋势， 且在相同压缩量下最大接触压力随密封圈正反面加载压力的变化规律均相似。

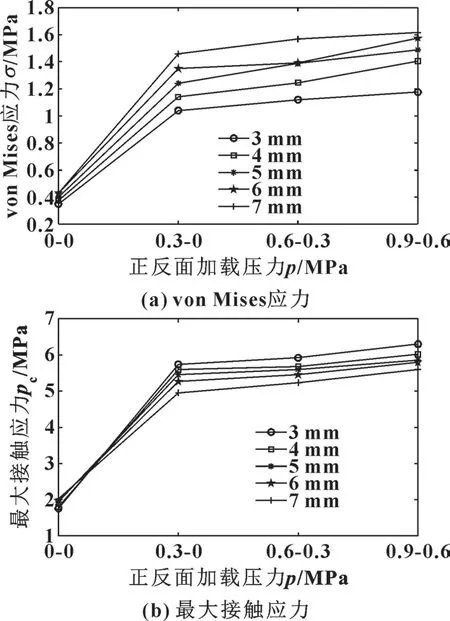
图11 不同压缩量下， 密封圈接触面von Mises 应力和最大接触应力随正-反加载面加载压力的变化Fig.11 Variation of von Mises stress （a） and maximum contact stress （b） with oil pressure on both sides of sealing ring under different compression amount

3 VD 密封的优化设计

由于VD 密封圈对油脂存在一定的依赖性， 且在低压缩量与高润滑油压力以及磨损的情况下会导致密封圈翻折泄漏， 故对其结构进行优化改良以进一步提高密封效果和提高其运行可靠性。 在密封圈压缩量较小时， 因产热和磨损等因素的影响， 密封圈容易产生翻折现象[7］。 然而虽然压缩量越大， 密封圈产生翻折的可能性越低， 但其接触面最大接触压力呈现下降趋势， 且接触面积也进一步增加， 影响密封圈密封效果。 为了改善和提高VD 密封圈在大的压缩量下的接触压力， 在VD 形密封圈的反面设计了支撑结构来提高密封效果和密封可靠性， 具体结构如图12 所示。

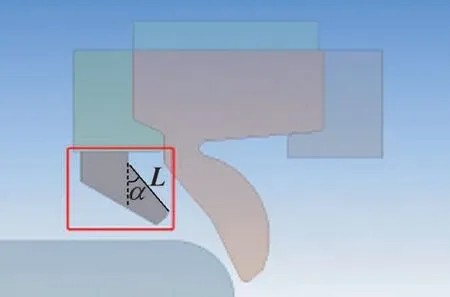
图12 优化的带反面支撑结构的VD 形密封圈Fig.12 Optimized VD sealing ring with reverse support structure

通过Box-Behnken 设计实验， 设计的带反面支撑结构的VD 形密封圈结构参数如表3 所示。

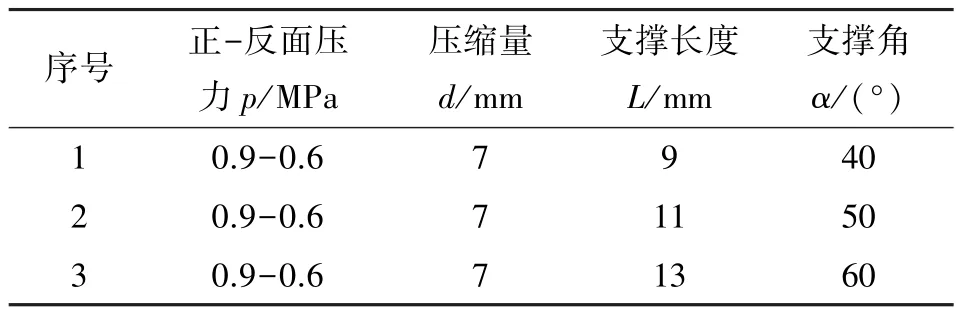
表3 Box-Behnken 设计的VD 形密封圈结构参数Table 3 Structure parameters of VD sealing ring with reverse support structure by Box-Behnken design

图13 所示为带反面支撑结构的VD 形密封圈曲面响应图。 通过曲面响应法， 预测出其最大接触压力出现在支撑长度L为59.499 mm、 支撑角α为9.345 3°处， 最大接触压力为6.976 4 MPa； 最小接触压力出现在L为40 mm、α为12.018°处， 最小接触压力为6.500 7 MPa。 而在压缩量7 mm， 正反面压力0.9-0.6 MPa 时， 原VD 形密封结构的最大接触压力为5.594 7 MPa。 因此引入反面支撑结构时， 提高了VD形密封结构接触面的接触压力， 提高幅值在0.906 ～1.381 MPa 之间， 即提高了16%～25%。

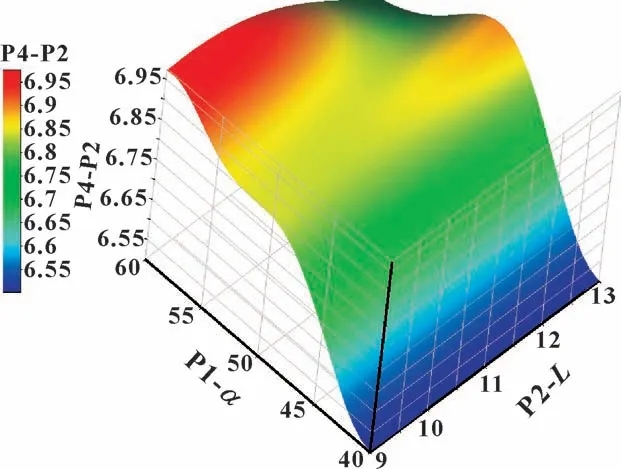
图13 带反面支撑结构的VD 形密封圈曲面响应图Fig.13 Response diagram of VD sealing ring with reverse support structure

4 结论

（1） 研究的VD 形密封结构的应力主要集中在VD 形密封圈齿形根部和VD 形密封圈顶部接触区域。配合面的压缩量是密封圈齿形根部产生弯曲应力集中的主要原因； 同时润滑油脂的压力作用， 使其根部应力集中的区域产生了偏移， 并导致根部的拉应力明显加剧。 齿形顶部接触区域存在的应力集中， 主要是由于润滑油脂压力的加载， 导致其接触面附近的赫兹接触应力显著增大。

（2） 在3～7 mm 范围内随着压缩量的增加， VD形密封圈接触面的最大von Mises 应力不断增加， 而接触面最大接触压力却不断下降。

（3） 在压缩量以及压差不变的情况下， 随着密封圈正反面接触压力的增加， 该VD 形密封圈接触面最大压力也保持相近幅值的上升。 说明当密封圈正反面压力变化时， 此密封圈结构设计保证了接触压力的裕度， 从而保证密封结构密封效果的稳定性。

（4） 通过曲面响应法对设计的带反面支撑结构的VD 形密封圈结构进行了优化， 得出在压缩量为7 mm， 正反面压力为0.9-0.6 MPa 条件下， VD 形密封结构的支撑角度为9.345 3°、 支撑长度为59.499 mm 时密封效果最好。