油管特殊螺纹接头密封及安全综合性能评价*

于 浩 成旭堂 练章华 丁亮亮 王 昊 陈宇航

（西南石油大学油气藏地质及开发工程国家重点实验室 四川成都 610500）

随着石油开采技术的发展， 油管服役环境也越来越苛刻， 而油管柱连接部位是最薄弱环节， 连接处螺纹结构强度与密封性能直接决定了油气井的开采寿命[1-3］。 特殊螺纹采用金属密封， 其密封性能直接取决于密封结构设计。 具有代表性的金属密封结构有国外的VAM 系列、 BLUE 系列、 FOX 系列， 国内宝钢的BGT 系列、 天钢的TP-CQ 系列等， 这些金属密封结构都可以满足复杂环境下密封性能要求， 已得到行业认可并广泛使用在各大油气田[4］。

目前， 关于油管特殊螺纹接头的研究相对较多。2015 年， 孙建安和王琍[5］通过试验和有限元手段分析了特殊螺纹接头上扣扭矩过程。 2016 年， 张瑞萍等[6］在考虑螺纹升角情况下建立三维有限元模型， 分析了不同温度对接头密封面和台肩完整性的影响。2017 年， 莫丽等人[2］针对常规特殊螺纹接头连接性能较差的问题， 提出了一种新型特殊螺纹接头结构并用有限元进行了强度分析。 2019 年刘奔等人[7］采用理论设计方法对偏梯形螺纹进行设计分析， 并通过有限元验证了其合理性。 2020 年， 曹银萍等[8］考虑材料和几何接触的双重非线性影响， 仿真分析了热循环载荷下螺纹接头的完整性。 2020 年， 张颖等人[9］建立了特殊螺纹接头密封面在动载荷作用下接触应力的力学模型， 分析了振荡载荷对油管柱接头的影响。2021 年， 何石磊等[10］开发了一种高性能油管特殊螺纹接头， 并利用有限元方法分析了其结构强度。 现阶段针对油管特殊螺纹接头的研究， 主要通过有限元与实验相结合的方法分析其全螺纹段结构强度及密封性能， 而针对全螺纹密封和台肩局部密封的对比分析研究较少。

本文作者首先建立特殊螺纹接头理论分析模型，提出螺纹整体密封和局部台肩密封指数， 并通过有限元手段研究复杂工况条件下密封性能的差异性， 最后通过综合结构完整性安全系数和密封性能安全系数给出特殊螺纹综合安全性能评价方法。

1 理论模型

油管特殊螺纹接头安全性评价应综合螺纹结构完整性和密封完整性两方面来评价， 单一评价对整个螺纹分析过于片面， 与实际偏差较大。

1.1 结构完整性理论

在高温高压井中， 油管特殊螺纹接头将承受内外压、 轴向载荷以及不同温变载荷的影响， 油管温度的变化， 将使得螺纹接头受热胀冷缩作用产生一定变形， 而油管在井下热变形受到井壁等空间位移约束产生一定热应力[11］。 根据线性热弹性原理， 应变包括温度变化和应力引起两部分应变， 由胡克定律分析得温载作用下油管应力应变[12］为

油管特殊螺纹接头在上扣后螺纹牙、 密封面及扭矩台肩面之间相互接触时， 利用Mises 屈服准则判定， 则有：

式中：E为油管材料弹性模量， MPa；μ为油管材料泊松比， 无量纲；G为油管材料剪切模量，MPa；αt为油管材料线膨胀系数， 1／℃； ΔT为温度变化量，℃；εx、εy、εz分别为X、Y、Z方向的主应变， 无量纲；σx、σy、σz分别为X、Y、Z方向的主应力， MPa；τxy、τyz、τzx分别为XY、YZ、ZX面的切应力， MPa；γxy、γyz、γzx分别为XY、YZ、ZX面的剪应变， 无量纲；σs为油管材料的屈服强度， MPa。

螺纹区域Mises 应力水平的大小及分布能反映螺纹结构整体的完整性， 若螺纹某一处高应力区出现大面积塑性贯穿区域， 则表示螺纹发生结构性破坏； 同时， 为分析实际工况环境下油管接头的安全性能， 以实际螺纹负载状态下螺纹平均应力和所选用材料屈服强度σs的比值， 引入特殊螺纹结构完整性评价系数κ1：

分析式（6） 发现， 特殊螺纹结构完整性评价系数κ1与整体平均应力成正比， 平均应力越大螺纹整体应力水平越大， 越容易发生失效破坏， 所以结构完整性评价系数越小代表螺纹结构越安全。

1.2 密封完整性理论

油管特殊螺纹最突出的优势为金属密封性能， 螺纹密封结构设计是整个螺纹设计研究的关键， 直接决定螺纹密封性的好坏。 以前许多API 螺纹[13］和特殊螺纹的研究者普遍认为， 金属对金属密封时只要接触面上有足够大的接触压力， 就可以保证其密封性。 然而特殊螺纹由于其结构设计的特殊性， 不同上扣扭矩或载荷作用都会导致接触面发生变化， 进而导致接触面上的接触压力发生变化， 因此， 单靠接触压力评价螺纹密封性是不可取的。 此外， 由于加工的原因， 密封面的光洁度只能维持在一定水平， 不可能完全光滑， 表面粗糙度使得密封面配合后仍存在微小的间隙。 根据流体力学， 流体通过间隙时产生的局部阻力ΔF取决于间隙的截面积和泄漏路径的长度[14］， 可表示为

接触面上的接触应力越大， 间隙的截面积就越小， 若二者成比例变化， 则有

泄漏阻力相当于沿泄漏路径累积的接触应力， 当气体或液体通过间隙时， 产生的阻力为

因此， 针对特殊螺纹密封能力可通过螺纹路径上有效密封长度Les上接触压力积分得到， 用W表示为

MURTAGIAN[15］通过物理试验和数值模拟方法研究了静态金属对金属密封面密封性能与密封接触应力剖面的经验函数关系， 提出的评价金属对金属密封性能参数Wa定义为

当极限泄漏率每15 min 为0.025 cm3， 提出特殊螺纹接头临界密封指数[16］为

式中： Δl为泄漏路径长度， mm；S为间隙截面积， mm2；pt为接触压力， MPa；pg为密封压力，MPa；pa为大气压力， MPa。

显然， 要使螺纹接头密封可靠， 需使W≥Wac，图1 所示为特殊螺纹临界密封曲线， 螺纹密封性能指数随压力比值的增大逐渐增大， 处于动态变化状态；曲线以上区域为安全无泄漏区域， 曲线以下区域为螺纹发生泄漏失效区域； 有螺纹脂时临界密封指数随压力比增加而增长缓慢， 无螺纹脂时临界密封性能随压力比增加而增长迅速。

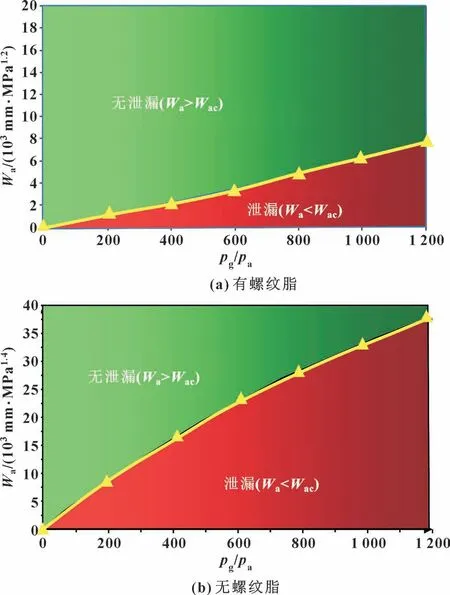
图1 特殊螺纹临界密封曲线Fig.1 Critical sealing curves of special thread： （a） with thread grease； （b） without thread grease

进一步研究发现， 通常人们认为的螺纹密封性能指数指的是全螺纹段上。 事实上在复杂工况条件下，虽然计算全螺纹所得的螺纹密封性能指数在安全范围内， 但当螺纹在台肩或密封面发生泄漏也会直接导致整个螺纹段失效。 因此， 在分析全螺纹密封性能指数W基础上， 应针对台肩及密封面重要部位单独进行分析， 提出更高的密封要求， 台肩及密封面局部密封性能指数Waj为

式中：Lt为台肩有效密封长度， mm；Lm为密封面上有效密封长度， mm。

当考虑油管特殊螺纹生产制造过程中加工尺寸偏差、 动载荷等其他条件对密封性能的影响， 给予一定的防泄漏安全余量， 引入特殊螺纹密封性能评价系数κ2：

密封性能评价系数κ2可用于评估所设计的油管特殊螺纹接头的金属对金属密封结构的防泄漏能力，κ2越大代表密封性能越好。κ2≥1 时表明螺纹不发生泄漏，κ2＜1 时， 表示螺纹出现泄漏失效。

最后， 通过综合油管特殊螺纹结构完整性和密封性能， 定义特殊螺纹综合安全系数Q为

结合式（6）、 （14） 和（15）， 综合安全系数Q受结构强度和密封性共同影响， 特殊螺纹结构完整性评价系数κ1越小， 综合安全系数Q越大， 代表螺纹结构整体越安全； 同样， 螺纹密封性能评价系数κ2与安全系数Q成正比， 密封性能评价系数越大， 螺纹综合安全系数也越大， 整体密封性能越好。

2 有限元模型建立

针对某ϕ88.9 mm 油管特殊螺纹， 在其结构尺寸基础上， 忽略螺旋升角影响， 考虑螺纹结构的复杂性， 即变形往往超出弹性范围， 属于几何非线性、 材料非线性以及接触非线性的多重耦合， 建立二维轴对称有限元模型。 由于接头两端的对称性， 取1／2 特殊螺纹接头分析。 考虑到圣维南边界效应对分析结果准确性的影响， 所建立管体长度大于管端至螺纹消失处长度的2 倍。 在接箍的右端施加Y向约束， 在管体左端施加轴向载荷F， 并在内壁施加内力p； 同时定义管体外螺纹路径由点A到点B全螺纹段为数据路径，方便后续分析螺纹路径上应力应变数值在不同工况条件下的变化情况。 图2 所示为有限元模型。

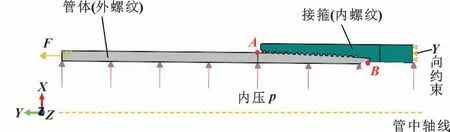
图2 有限元模型Fig.2 Finite element model

图3 所示为网格模型， 螺纹段采用非线性变形的轴对称四边形单元， 为节省计算成本， 螺纹连接部分、 尾端以及台肩处进行网格细化处理， 网格密度为0.02， 其他地方的网格相对粗糙； 采用过渡单元对螺纹与管道结构化网格之间的网格进行建模， 保证计算结果的准确性。

表1 给出了材料力学性能参数。 油管特殊螺纹接头均采用P110 钢级材料， 通过拉伸实验数据输入真实应力应变数值， 密封面接触采用库仑摩擦准则， 摩擦因数与螺纹脂有关， 一般取0.02[14］。 图4 所示为P110 材料应力应变曲线。

图4 P110 材料应力应变曲线Fig.4 Stress-strain curve of P110 material

3 仿真结果及分析

3.1 上扣扭矩影响分析

通过对特殊螺纹施加轴向0.1 mm 和径向0.16 mm 过盈， 模拟油管螺纹上扣状态， 上扣扭矩为4 410 N·m， 通过改变螺纹整体前后温度， 分析了温差作用下对螺纹结构的影响。 图5 示出了不同温差下最佳上扣扭矩状态Mises 应力分布。 可以看出， 上扣后螺纹段应力水平相对较低， 最后一扣靠近退刀槽位置和台肩密封面上应力水平相对较高； 随着温差增大， 整体螺纹段受材料和结构热胀冷缩变形影响， 应力水平有明显提高， 最大高达1 372 MPa， 但未出现明显大面积应力高强度区域。

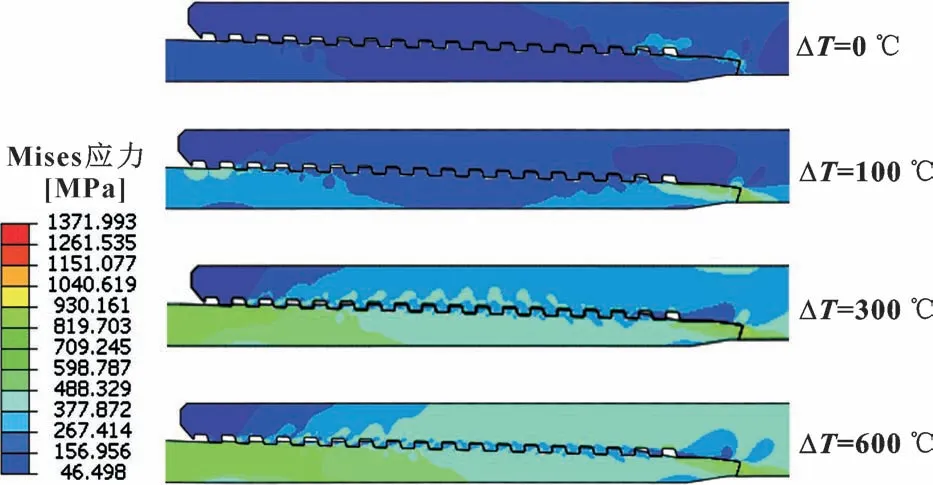
图5 不同温差下上扣状态Mises 应力分布Fig.5 Mises stress distribution in the make-up state under different temperature difference

图6 所示为不同温差下管体外螺纹路径上Mises应力分布及大小。 可见， 沿管体外螺纹路径上两侧受接头结构变形挤压应力水平相对较高， 中间螺纹齿部分应力分布相对均匀， 略有波动； 随着温差的增大接头整体应力水平均有明显提升， 但最大应力依旧分布在管体接头两侧， 受螺纹结构影响波动分布。

图6 不同温差下沿管体外螺纹路径Mises 应力分布Fig.6 Mises stress distribution along the external thread path of the pipe body under different temperature difference

图7 所示为螺纹接头接触压力分布。 可以看出，螺纹处于上扣状态时， 台肩和密封面受到结构挤压产生较大接触应力， 为770 MPa； 最大接触压力位于螺纹尾端和退刀槽最后一扣位置， 为1 037 MPa； 受结构影响上扣后螺纹承载面接触压力相对较大。

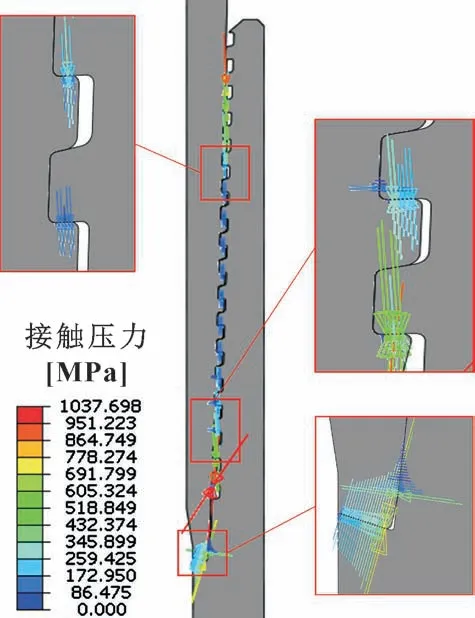
图7 螺纹接头接触压力分布Fig.7 Contact pressure distribution of threaded joints

图8 所示为不同温差下沿管体外螺纹路径接触压力分布。 上扣后， 受温差变化影响， 管体外螺纹上接触压力也发生明显变化， 接触压力呈现凹型分布， 两侧较大， 中间波动均匀分布； 随着温差的增大整体接触压力均有明显提升； 由于螺纹段相互啮合处存在空隙， 接触压力存在为0 区域， 呈现独立分段分布。

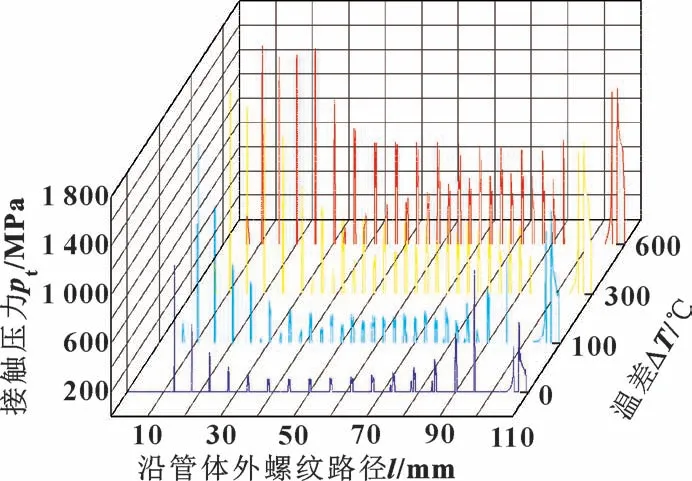
图8 不同温差下沿管体外螺纹路径接触压力分布Fig.8 Contact pressure distribution along the external thread path of the pipe body under different temperature difference

3.2 内压变化影响分析

通过对接头施加不同内压， 分析了接头处Mises应力随内压的变化， 结果如图9 所示。 随着内压的增大， 螺纹接头Mises 应力逐渐增大， 管体外螺纹受内压变化影响应力变化迅速； 台肩及密封面随内压的增大应力水平达370 MPa， 但远低于材料屈服强度， 未发生结构失效破坏。

图9 螺纹接头处Mises 应力随内压变化Fig.9 Mises stress changes of threaded joints with internal pressure

图10 所示为不同内压下沿管体外螺纹路径Mises应力分布。 管体外螺纹路径上Mises 应力随着内压的增大逐渐增大， 最大应力出现在第一二扣和最后一扣退刀槽处， 出现部分高应力塑性变形， 整体呈现凹型分布；螺纹齿啮合部位应力分布相对均匀， 总体相对较低。

图10 不同内压下沿管体外螺纹路径Mises 应力分布Fig.10 Mises stress distribution along the external thread path of the pipe body under different internal pressure

图11 所示为不同内压下沿管体外螺纹路径接触压力分布。 随着内压的增大， 沿管体外螺纹接头接触压力逐渐增大， 最大应力出现在最后一扣退刀槽位置； 螺纹啮合处承载面和径向接触部位接触压力分布相对均匀， 整体接触压力沿轴向呈现凹型分布趋势。

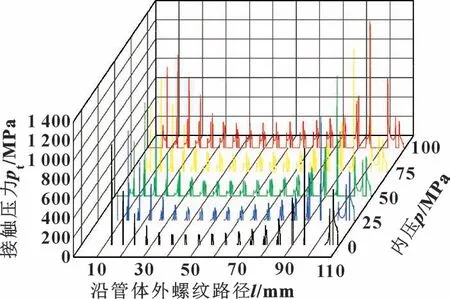
图11 不同内压下沿管体外螺纹路径接触压力分布Fig.11 Contact pressure distribution along the external thread path of the pipe body under different internal pressure

图12 示出了螺纹密封指数随内压变化曲线。 随着内压的增加整体密封指数Wa逐渐增大， 而台肩密封指数Waj随着内压的增加先逐渐增大后趋于平缓，内压越大增加幅度越小。 无论有无螺纹脂， 整体密封指数Wa均大于临界密封指数， 表明螺纹整体密封性能完好， 无泄漏发生。 有螺纹脂时当内压超过62 MPa 时台肩密封指数Waj小于临界密封指数Wac， 密封失效（见图13 （a） ）； 无螺纹脂时当内压超过23 MPa 时就已经发生泄漏（见图13 （b） ）。 可见有螺纹脂时螺纹接头台肩抗密封性能更好， 不易发生泄漏， 更安全。

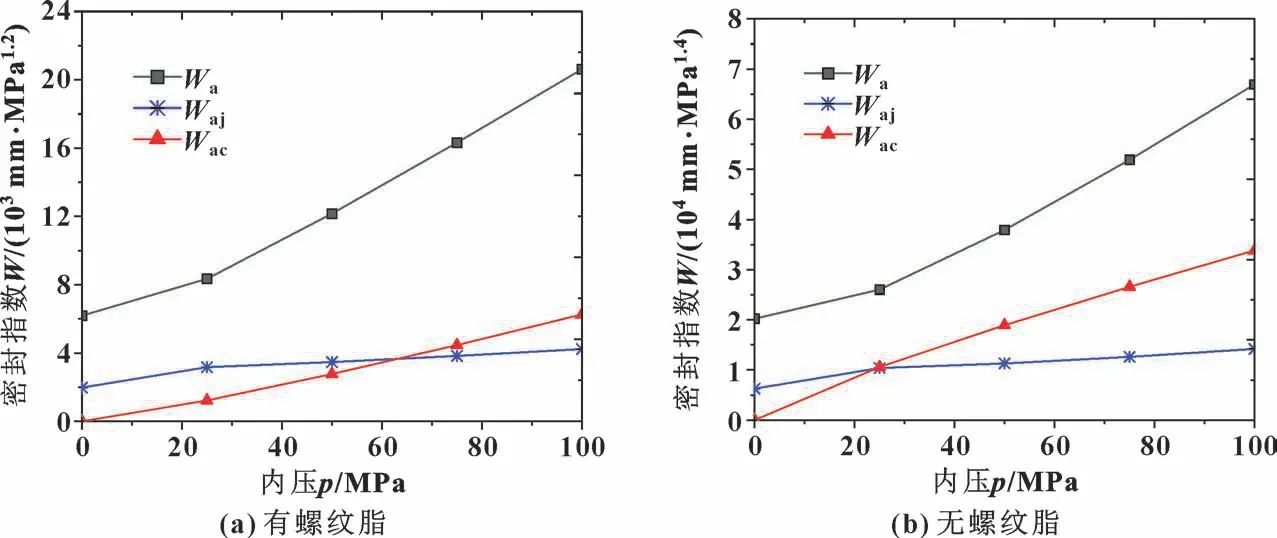
图12 螺纹密封指数随内压的变化Fig.12 Thread sealing index changes with internal pressure： （a） with thread grease； （b） without thread grease

3.3 轴向载荷变化影响分析

对特殊螺纹接头施加轴向拉伸载荷， Mises 应力随轴向拉伸载荷的变化如图13 （a） 所示。 随着载荷的增加， 螺纹整体应力水平有明显提高， 当载荷F＝1 200 kN 时管体以及接头最后一扣退刀槽位置出现明显应力集中， 最大高达922 MPa。 台肩及密封面随着轴向拉伸载荷的增加逐渐发生分离， 应力水平相对较低。

改变载荷施加方向， 对特殊螺纹接头施加轴向压缩载荷， 分析了Mises 应力随轴向压缩载荷的变化，结果图13 （b） 所示。 伴随载荷的不断增大， 管体及接头第一二扣出现应力集中现象； 台肩及密封面受挤压也出现较高应力区域， 最大应力为924 MPa。

图13 Mises 应力随轴向拉伸载荷和轴向压缩载荷的变化Fig.13 Mises stress changes with axial tensile load and axial compression load： （a） effect of axial tensile load； （b） effect of axial compression load

图14 所示为轴向载荷作用下沿管体外螺纹Mises应力的变化。 在轴向载荷作用下管体外螺纹路径上Mises 应力分布相对均匀， 受螺纹几何结构限制台肩及最后一扣位置应力水平相对较高。 其中在轴向拉伸载荷作用下， 螺纹承载面受力较大， 应力水平也较高， 而在压缩载荷作用下， 除台肩外导向面也承受一部分轴向压缩载荷， 应力分布呈现波动周期分布。螺纹啮合部分在拉伸工况下的应力水平高于压缩工况； 台肩部位在压缩工况下的应力水平高于拉伸工况； 整体上轴向拉伸下应力水平波动幅度远高于压缩工况。

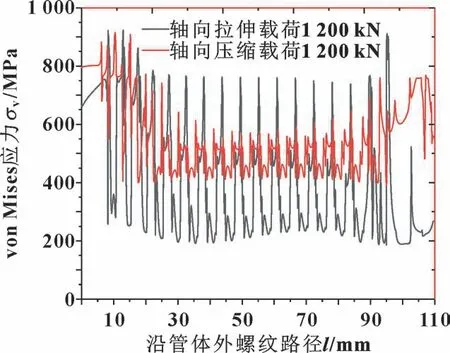
图14 轴向载荷作用下沿管体外螺纹Mises 应力的变化Fig.14 Mises stress changes along the external thread of the pipe under axial load

图15 （a） 所示为在拉伸工况下台肩处接触压力分布云图。 可见， 拉伸工况下下台肩部位发生分离，致使接触压力为0； 密封面受拉伸载荷作用， 接触压力由下及上呈现逐渐增大趋势， 最大接触压力为925 MPa。 图15 （b） 所示为在压缩载荷工况下台肩处接触压力分布云图。 可见， 受轴向压缩载荷影响， 台肩接触压力较大， 最大为852 MPa； 密封面接触压力受结构影响呈现凹型分布， 最大为994 MPa。

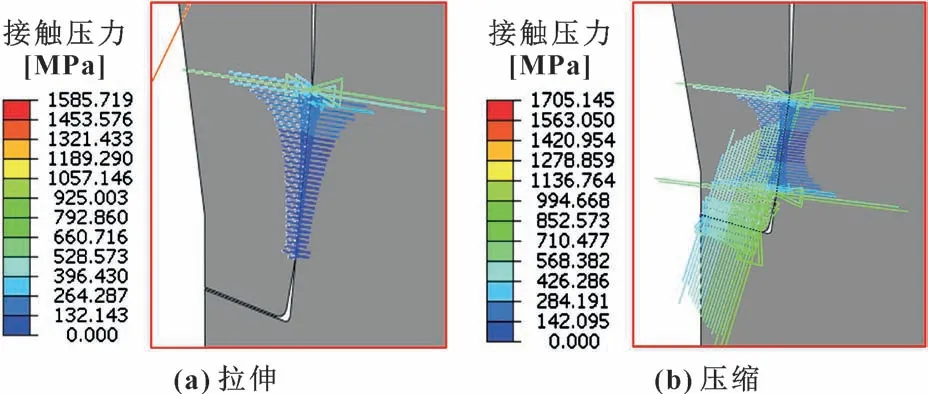
图15 拉伸和压缩工况下台肩处接触压力分布Fig.15 Contact pressure distribution of threaded joints under tensile and compression conditions： （a） tensile condition； （b） compression condition

图16 所示为轴向载荷作用下沿管体外螺纹接触压力的变化。 可见， 沿管体外螺纹路径接触压力呈现凹型分布， 两侧接触压力相对集中； 轴向拉伸状态下台肩处接触压力为0， 最大接触压力出现在第一二扣及退刀槽位置， 承载面为主要接触压力分布位置； 轴向压缩工况下类似拉伸工况， 但由于导向面也受到一定挤压， 接触区域较多， 曲线分布也相对较为密集。

图16 轴向载荷作用下沿管体外螺纹接触压力变化Fig.16 Contact pressure changes along the external thread of the pipe body under axial load

图17 示出了不同轴向拉伸载荷下的螺纹密封指数。 有无螺纹脂时螺纹整体密封指数Wa均远大于临界密封指数Wac， 并随轴向拉伸载荷的增加逐渐增大， 表明螺纹接头安全可靠， 无泄漏发生。 但台肩及密封面由于受到拉伸载荷的影响， 台肩局部密封指数Waj均小于临界密封指数Wac， 并随拉伸载荷的增加逐渐减小， 表明台肩部位已经发生密封失效， 相对于螺纹接头整体也处于不安全状态。

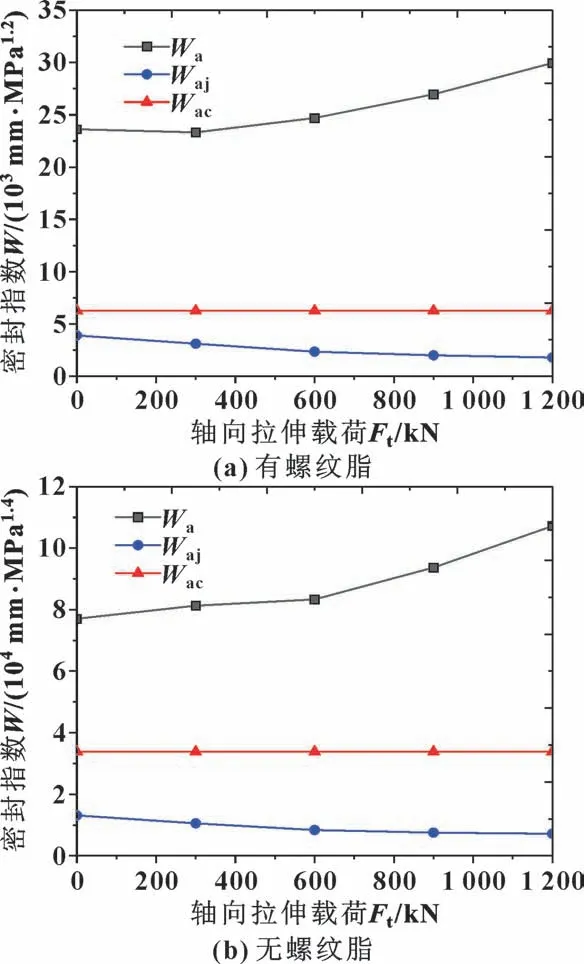
图17 螺纹密封指数随轴向拉伸载荷的变化Fig.17 Thread sealing index changes with axial tensile load：（a） with thread grease； （b） without thread grease

图18 示出了不同轴向压缩载荷下的螺纹密封指数。 如图18 （a） 所示， 有螺纹脂时整体密封指数Wa随轴向压缩载荷的增加逐渐增大， 并远远大于临界密封指数Wac； 而台肩部位受压缩载荷影响， 存在临界安全载荷430 kN， 当压缩载荷小于430 kN 时台肩局部密封指数Waj小于临界密封指数Wac， 存在泄漏风险。 如图18 （b） 所示， 无螺纹脂时整体密封指数Wa均远大于临界密封指数Wac， 而在轴向压缩载荷1 200 kN 以下， 台肩局部密封指数Waj随压缩载荷的增加逐渐增大， 但均小于临界密封指数Wac， 处于泄漏状态。 因此， 油管接头涂抹螺纹脂将大大增强螺纹接头的防泄漏能力。

图18 螺纹密封指数随轴向压缩载荷的变化Fig.18 Thread sealing index changes with axial compression load：（a） with thread grease； （b） without thread grease

4 综合安全系数评价

通过综合分析油管特殊螺纹接头结构完整性能和密封性能， 得到综合安全系数Q随不同载荷工况条件下的变化情况。 图19 所示为综合安全系数随内压变化。 可见， 随着内压的增加综合安全系数将逐渐降低， 螺纹接头的可靠性也逐渐降低， 螺纹接头有泄漏风险； 有螺纹脂时整体安全系数Qa1和台肩局部安全系数Qj1相对于无螺纹脂时Qa2和Qj2， 变化趋势相同，但有螺纹脂时的安全系数要高于无螺纹脂时， 表明螺纹脂对综合安全系数影响显著。

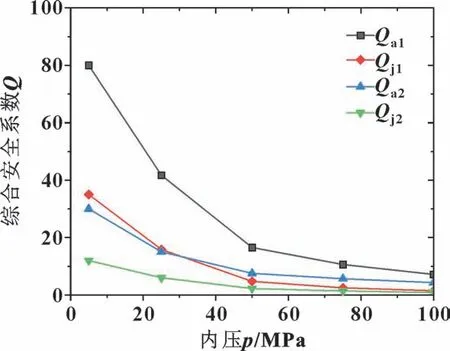
图19 综合安全系数随内压的变化Fig.19 The comprehensive safety factor changes with internal pressure

图20 所示为综合安全系数随轴向载荷变化。 在轴向载荷作用下， 有螺纹脂的整体安全系数Qa1和无螺纹脂的整体安全系数Qa2， 均随载荷的增加而逐渐增大。 在拉伸载荷工况下， 有螺纹脂的局部台肩安全系数Qj1和无螺纹脂的局部台肩安全系数Qj2， 随载荷增大而逐渐减小； 在压缩载荷工况下， 局部台肩安全系数均随载荷的增大先增大后趋于平缓， 这是由于在过大轴向载荷下管体已经发生结构变形破坏。 螺纹整体安全系数Qa远高于台肩局部安全系数Qj， 因此，针对不同载荷工况应对整体和局部进行综合评价。

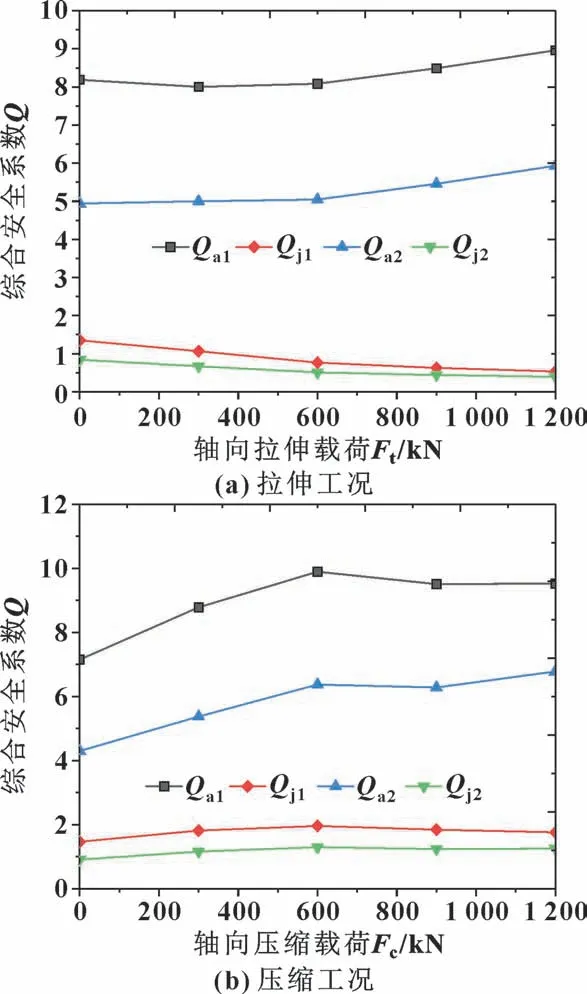
图20 综合安全系数随轴向载荷的变化Fig.20 The comprehensive safety factor changes with the axial load： （a） axial tensile condition；（b） axial compression condition

5 结论

（1） 综合特殊螺纹接头结构完整性和密封完整性， 建立了特殊螺纹接头综合安全评价方法。

（2） 在不同工况条件下特殊螺纹接头Mises 应力和接触压力呈现凹型分布趋势， 首尾以及最后一扣退刀槽位置是应力相对集中的薄弱部位。

（3） 随温差增大， 特殊螺纹接头整体受材料和结构热胀冷缩变形的影响， 应力水平有明显提高； 同时， 受内压影响整体结构应力水平和密封性变化明显； 轴向拉伸载荷导致台肩部位逐渐分离， 影响了螺纹接头的密封性能。

（4） 螺纹脂的添加提高了螺纹接头整体和局部的密封和安全性能； 内压的增大将导致螺纹接头安全性降低； 拉伸工况下螺纹整体安全性上升， 而局部台肩处发生分离， 导致安全性反而逐渐降低； 压缩状态下安全性逐渐上升， 但由于管体抗压性能影响， 过大载荷下螺纹接头安全性能也会下降。