柔性石墨填料结构改进及密封性能研究*

金熙来 章兰珠 倪 焱

（华东理工大学机械与动力工程学院 上海 200237）

航空航天、 石油化工、 核工业等专业领域常使用阀杆填料密封机构来实现对流体介质的动密封。 影响该机构密封性能的因素包括阀杆运动的方式及精确度、 阀杆填料接触面的情况、 介质情况、 填料结构、填料压盖的预紧力等[1-2］。

柔性石墨的应用始于20 世纪60 年代末， 该材料具有较高的弹性、 热稳定性和耐化学性[3］。 柔性石墨填料于1970 年投入市场， 我国从1978 年开始研究进而应用石墨填料， 并逐渐取代对人体有危害的石棉填料[4-5］。 石墨填料除无毒外， 密封性能也优于石棉填料[6］。 目前投入使用的柔性石墨填料组大多由数个平口环组合而成， 被压紧后， 内部应力沿轴向衰减， 越靠近压盖的填料环受力越大。 然而， 石墨填料组的首环通常会混入金属丝来增加强度以保护中间的纯石墨填料环， 其密封性能则较弱， 因此石墨填料组的结构具有改进空间。 研究表明[7］， 使用V 形填料组能改善填料组受力情况， 且填料环的径向形变也优于平面环。

许多研究人员利用多孔介质相关理论与有限元仿真来研究密封件， 柔性石墨填料内部存在孔隙， 也可视为多孔介质。 周先军等[8］考虑多种因素， 建立了非金属垫片的多孔介质泄漏模型。 顾伯勤[9-10］利用流动方程得到垫片密封的基本参数， 利用图算法实现对非金属多孔介质泄漏的预测。 包超英等[11］基于多孔介质模型建立密封渗流模型， 提出一种密封端面间泄漏率的计算方法并总结了泄漏率的影响因素。 MEHDI和ABDEL-HAKIM[12］建立了3 种表征多孔压缩石墨填料泄漏预测模型并进行对比研究。 近期， 对于细观尺度下多孔介质中流体流动理论的研究正由线性渗流理论向物理化学、 非牛顿、 多尺度非线性渗流发展[13］。

目前虽然已有研究人员利用多孔介质理论来进行柔性石墨填料泄漏率的有限元仿真计算， 但这些仿真模型所使用的多孔介质参数都只有初始状态下（填料被压紧后， 阀杆开始运动前） 的参数， 并未考虑机构运行过程中填料受力状况变化对这些参数的影响。 本文作者根据柔性石墨填料环的制作工艺及工作方式对目前广泛应用的平面环填料组进行结构改进，设计了一种V 形填料组， 并结合磨损试验及压汞法测试所得的柔性石墨的摩擦磨损特性及孔隙参数， 实现有限元仿真中结构仿真模型的更新与多孔介质模型的建立， 来对比2 种结构填料组的密封性能。

1 填料结构优化方案

1.1 填料结构设计

平面环填料组及目前常见的V 形填料组结构如图1 所示[14］， 图1 （b）、 （c） 中的2 种填料组通过人为制造应力集中改变填料环受力， 提升填料组密封性能。 柔性石墨填料组中， 填料组的首末环通常是用于刮去阀杆表面石墨粉末， 并采用了保护纯石墨环的金属丝加固石墨环， 因此起主要密封作用的是中间配置的纯石墨环。 对比2 种V 形结构： 结构1 是通过制造应力集中增大中间2 个填料环内部的应力， 与石墨填料组的特点相匹配； 结构2 则适用于所有密封环共同起密封作用的情况， 与石墨填料工作特点不符。

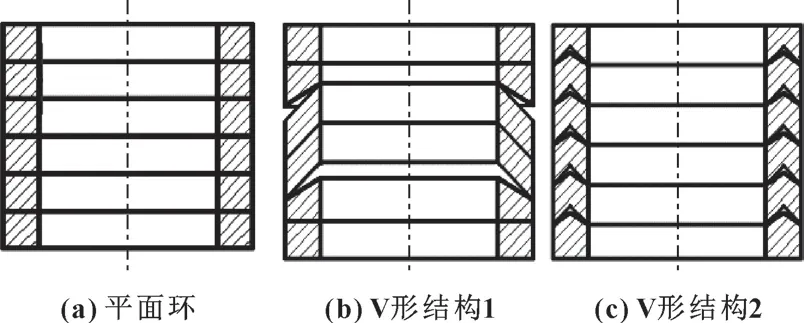
图1 典型的填料组合结构的截面型式Fig.1 Typical combination structures and section types of packing：（a）planar rings； （b）V type structure 1； （c）V type structure 2

根据上述结论， 选择将平面环填料组改进为V 形结构1， 填料组在改进前后的结构与尺寸如图2 所示。

有限元计算的完成需要柔性石墨填料的密度、 弹性模量及泊松比3 个参数。 密度由填料环质量除以体积得出， 填料环质量由电子天平测得， 测量对象为浙江国泰萧星密封材料股份有限公司生产的金属丝石墨、 纯石墨填料环各10 个， 取平均值保留一位小数。王夫清[15］曾使用该公司的填料测定了不同压紧力下填料的轴向应变及周向应变， 填料的弹性模量及泊松比可由此求得。 最终纯石墨环设置参数如下： 密度1.5 g／cm3， 弹性模量500 MPa， 泊松比0.46。 刮垢环密度取1.8 g／cm3， 由于其弹性模量和泊松比与纯石墨环接近， 在仿真时取相同值。 虽然柔性石墨为各向异性材料， 但压紧力方向固定为轴向， 因此只需一组弹性模量与泊松比。

1.2 有限元模型建立

阀杆填料密封结构的2D 几何模型如图3 所示，该模型中包含填料函、 阀杆、 填料压盖以及填料。 在计算模型中的压盖表面设置力载荷， 代表压紧力。 模型每部分的温度统一设为27 ℃。 填料与阀杆、 填料与填料函的摩擦因数参照2.1 节表1 中的数值进行设置， 由该表中的数据求得各组试验中摩擦因数平均值为0.10。 因此模型中填料与阀杆、 填料函的摩擦因数设置为0.1。

图3 结构仿真2D 几何模型（平面环）Fig.3 2D structure simulation model （planar rings）

对模型施加约束与载荷如下：

对填料函侧面施加固定约束； 对压盖施加21 kN的压紧力， 此后保持压盖位置不变。 求解器中开启大变形； 对阀杆施加位移载荷， 模拟其往复运动。 上述载荷设置为分步施加： 首先对压盖施加压紧力， 再将其改为位移载荷以固定压盖位置， 最后在阀杆上添加位移载荷模拟阀杆的往复运动， 先向填料函外移动，再向填料函内移动至原位。 如图4 所示， 时间步长为1 s， 阀杆行程100 mm。 前5 个时间步对压盖施加压紧力， 在此期间阀杆不运动。 从第6 个时间步开始对阀杆施加位移载荷。

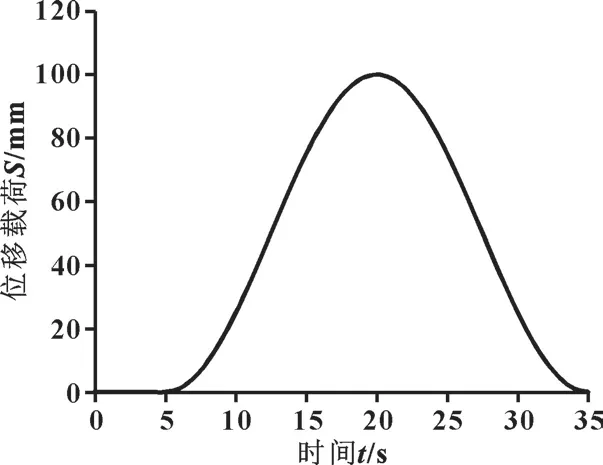
图4 阀杆位移载荷Fig.4 Displacement of the stem

密封机构内部流场仿真模型如图5 所示， 模型分为两部分： 气体入口附近的普通流体域以及填料所对应的多孔介质区域。 普通流体域对应阀杆与填料函间的间隙（图5 中的介质通道）。 介质的入口设在介质通道最右端边界， 出口设立在填料区域的最左端边界， 其余外表面设置为壁面。 V 形填料环流体域模型相对复杂， 由于二三环、 四五环间存在间隙， 需单独再建立2 个普通流体域。 为准确划分壁面边界， 将模型中的末环分割为两部分。

图5 填料密封流体区域二维模型（V 形填料）Fig.5 2D model of fluid domain of of packing seal （V type packing）

将石墨填料流场模型导入Fluent 后， 选用双精度求解器、 湍流模型k-epsilon， 打开能量方程， 将所有区域设为流体区域， 并将材料设为密度可变的氦气。 随后通过式（1）、 （2）、 （3） 计算并输入各多孔介质区域的黏性阻力系数， 将流场入口设置为压力入口， 气压为0.2 MPa。

式中：α0为未受力时的渗透率， 其倒数即为未受力时的黏性阻力系数；ε为孔隙度；Dp代表多孔介质颗粒直径， 可利用分形多孔介质理论中的最大孔隙模型[16］计算Dp的值；Ra为平均孔喉半径；σ代表多孔介质受压的平均有效应力；α代表受压填料的渗透率， 其倒数为受力时的黏性阻力系数； e 为自然对数的底数； 系数-0.211 参考了文献[9］中的测量结果。

初始化方式选用标准初始化， 初始化参数中气体压力输入入口介质压力值0.2 MPa， 温度300 K。

1.3 密封性能评价

使用参数化仿真计算不同运行次数下密封机构理论泄漏率。 首先将6 个填料环与阀杆间接触的偏移量设为可变参数， 初始值为0。 在一定次数的机械循环后根据磨损试验结果对接触偏移量进行更新。 通过公式（1） — （3）、 石墨填料的孔隙参数以及填料应力获得每个填料环的渗透率。

接触偏移量的更新通过编写的IronPython 脚本来实现， 该脚本根据2.1 节中得出的磨损特性， 由仿真结果中单一填料环与阀杆间的接触应力计算接触面偏移量并进行赋值， 实现接触状态的更新， 最终得到多次机械循环过程中密封机构泄漏率的变化情况， 实现密封性能分析。

1.4 材料参数测定

磨损试验使用的仪器为环块摩擦磨损试验机， 试样如图6 所示。 柔性石墨试样受加工工艺的限制， 只能制作为环状试样， 内径43.45 mm， 锥度20°， 外径49.22 mm。 块试样选用阀杆常用材料40Cr 合金钢，尺寸为12.32 mm×12.32 mm×19.05 mm。 磨损后环试样的质量损失由电子天平测量， 接触应力通过赫兹公式计算。

图6 磨损试验示意及试样Fig.6 Schematic of wear test and test sample

利用FLUENT 软件对填料函及填料内部流场进行模拟仿真时， 需利用分形多孔介质理论得出填料的渗透率。

计算石墨填料渗透率所需参数由图7 所示的美国康塔仪器公司的全自动孔径分析仪POREMASTER 进行测试。 将样品放置于样品管内， 自动抽真空后， 步进加压回填汞至样品管顶部， 实现相关参数测量。 利用压汞法测得多孔介质区域石墨填料孔隙度ε后， 可使用Ergun 公式获得黏性阻力系数与惯性损失系数，惯性损失系数仅在流体流速较快时才设置， 因此不进行计算。

图7 全自动孔隙分析仪Fig.7 Automatic aperture analyzer

2 柔性石墨材料参数测定

2.1 摩擦因数

将试样洗净烘干后称质量， 然后装在实验台上，启动电机（由于石墨环抗剪切载荷的能力较弱， 圈数、 转速均不宜过高， 因此转速设为6 r／min， 旋转150 圈）， 最后取下环状试样， 洗净烘干称质量。 试验力最小值设为50 N， 最大值设为400 N， 每50 N进行一次试验， 测量8 组数据。

实验结果如表1 所示， 接触应力是由柔性石墨材料参数配合赫兹公式计算得出， 磨损体积由质量损失得出， 相对滑动距离通过旋转圈数以及由游标卡尺所测得的试样磨损区域的外径得出。

表1 摩擦磨损试验结果Table 1 Friction and wear test results

表1 中单位长度磨损体积与接触应力可近似视为线性关系， 为确定该应力范围内摩擦副的磨损特性，以最小二乘法拟合直线， 如图8 所示。 最终得出单位长度磨损体积随接触应力的变化率为6.82×10-5mm3／（mm·MPa）， 常数项为-1.15×10-4mm3／mm。

图8 单位长度磨损体积随接触应力的变化状况及线性拟合结果Fig.8 Change of wear rate with contact stress and linear fitting result

2.2 孔隙参数

柔性石墨填料组中的金属丝增强石墨环与纯石墨环的多孔介质参数由图7 所示设备进行测定。 测试后得知， 金属丝石墨孔隙度为26.4%， 纯石墨孔隙度为18.1%。 对流体渗透存在贡献的孔隙的相关参数如表2 所示。

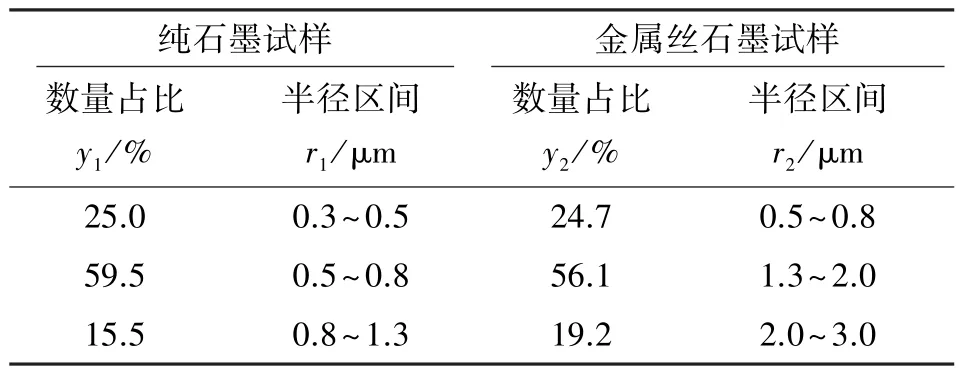
表2 孔隙分布Table 2 Pore distribution

由测试结果， 可计算2 种填料的平均孔隙半径：纯石墨为0.63 μm， 金属丝石墨为1.90 μm。

3 填料初始状态对比

对一套填料中的填料环进行编号， 距压盖最近的填料环命名为1 环， 最远的为6 环。

通过有限元仿真软件ANSYS 中的稳态结构模块对2 种结构的填料组被压紧后的变形量、 等效应力、有效应力、 与阀杆间的接触应力、 摩擦力及泄漏率进行对比。

3.1 变形量对比

对2 种填料都施加21 kN 的压紧力后， 经过计算发现平面环填料密封机构的压盖位移约为0.6 mm，而V 形环密封机构的压盖位移则达到了约2.3 mm，显著大于平面环填料密封机构。 2 种填料本身变形量的分布（阀杆未运动时） 如图9 所示。 图9 （a）中， 平面环变形量最大值约为0.56 mm， 图9 （b）中， V 形环变形量最大值约为2.31 mm。 V 形环填料的变形量明显更大， 这是由于V 形环填料中的2、3 环与4、 5 环之间存在空隙， 使得V 形填料组变形更加容易。

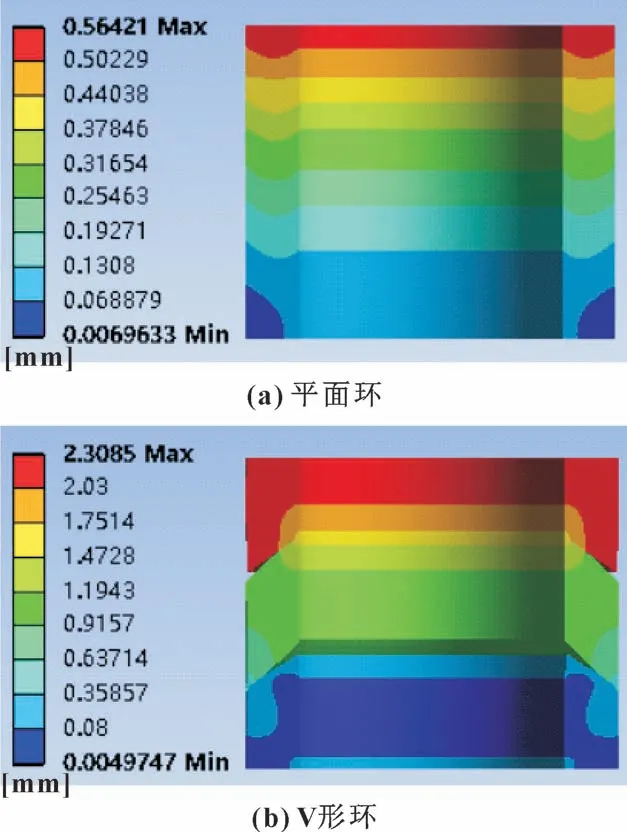
图9 填料环初始变形量对比Fig.9 Comparison of the initial deformation of the pressed packing ring： （a） planar rings； （b） V type rings

3.2 应力对比

文中对填料在初始状态下的等效应力、 有效应力进行对比。 图10 所示为2 种结构的石墨填料环在21 kN 压紧力下的等效应力分布云图。 图10 （a） 中，平面环等效应力最大值约为21.38 MPa， 越是远离压盖的环等效应力越小， 末环有一处应力较大， 原因是该处与填料函内介质通道的边缘接触， 产生应力集中。 图10 （b） 中， V 形环等效应力最大值位于应力集中区域， 约为83.60 MPa； 远离应力集中处的位置等效应力显著低于该值。

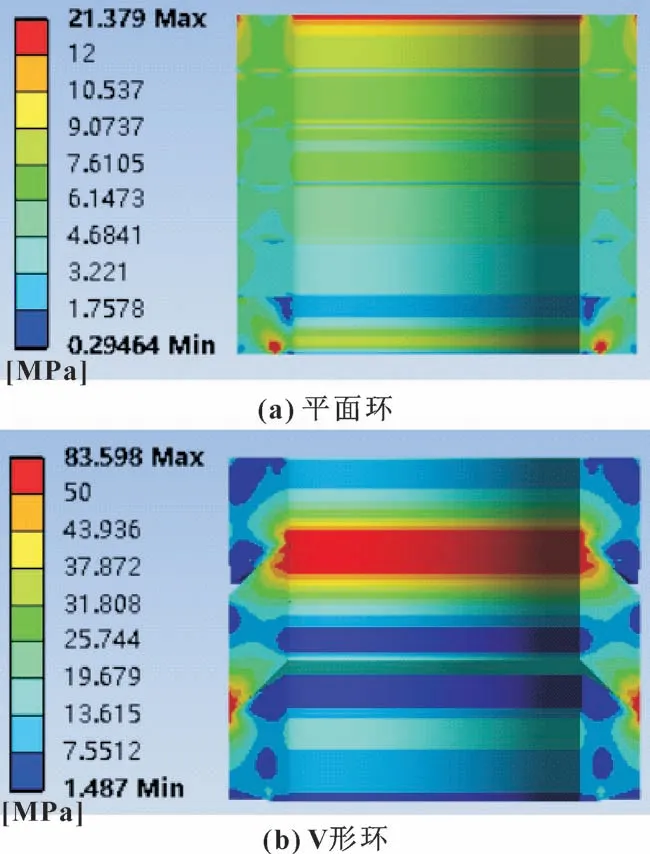
图10 填料环初始等效应力分布对比Fig.10 Comparison of the initial equivalent stress of the pressed packing ring： （a） planar rings； （b） V type rings

如1.1 节中所述， 柔性石墨填料组中的首末两环并不作为密封的主要功能环， 因此V 形填料中密封功能环（尤其是3、 4 填料环） 的应力明显增大这一现象有利于提升填料组密封效果。

根据式（3）， 计算填料渗透率时需要知道填料的有效应力。 有效应力是多孔介质在荷载作用下通过粒间接触面传递的平均法向应力。 根据该定义， 将每个填料环内部轴向应力的平均值作为该填料环的有效应力。

表3 给出了初始状态下不同结构的2 种填料所受有效应力。 由于阀杆运动方向会影响填料所受摩擦力的方向， 表3 中按阀杆运动方向分别给出了填料内部的有效应力。 可见， 平面环填料组中， 越接近压盖的填料环有效应力越大， 阀杆运动方向对有效应力的值影响较大； V 形环填料组中， 除首环外， 3、 4 环受到的有效应力也较大， 且阀杆运动方向对有效应力分布影响较小。

表3 填料环有效应力对比Table 3 Comparison of the effective stress

3.3 摩擦力对比

阀杆填料密封机构运行过程中， 在保证阀杆与填料紧密贴合的前提下， 为降低填料的磨损速率及机构能耗， 阀杆受摩擦力应尽可能小。 表4、 表5 给出了填料环与阀杆间的接触应力及填料组与阀杆间的摩擦力。 初始状态下V 形填料组的填料环与阀杆间的接触应力普遍较低， 且从整体来看， V 形填料组对阀杆的摩擦力也明显小于平面环填料组。

表4 填料环与阀杆间的接触应力对比Table 4 Comparison of the contact stress between the stem and the packing ring

表5 阀杆所受摩擦力对比 单位：kNTable 5 Comparison of the friction Unit：kN

3.4 介质流量对比

根据1.2 节所述流场仿真模型计算初始状态下阀杆填料密封机构内部氦气的流量， 如表6 所示。

表6 密封机构内部氦气流量对比 单位： 10-10 kg·s-1Table 6 Comparison of the helium flux in the sealing mechanism Unit： 10-10kg·s-1

由计算结果可知平面填料组在阀杆外移时， 密封效果略优于V 形环， 但阀杆内移时V 形环密封效果明显更好， 且V 形填料组的密封效果受阀杆运动方向的影响不大。

通过后处理软件CFD-Post 观察初始状态填料区域内氦气介质的压力分布， 如图11 所示。

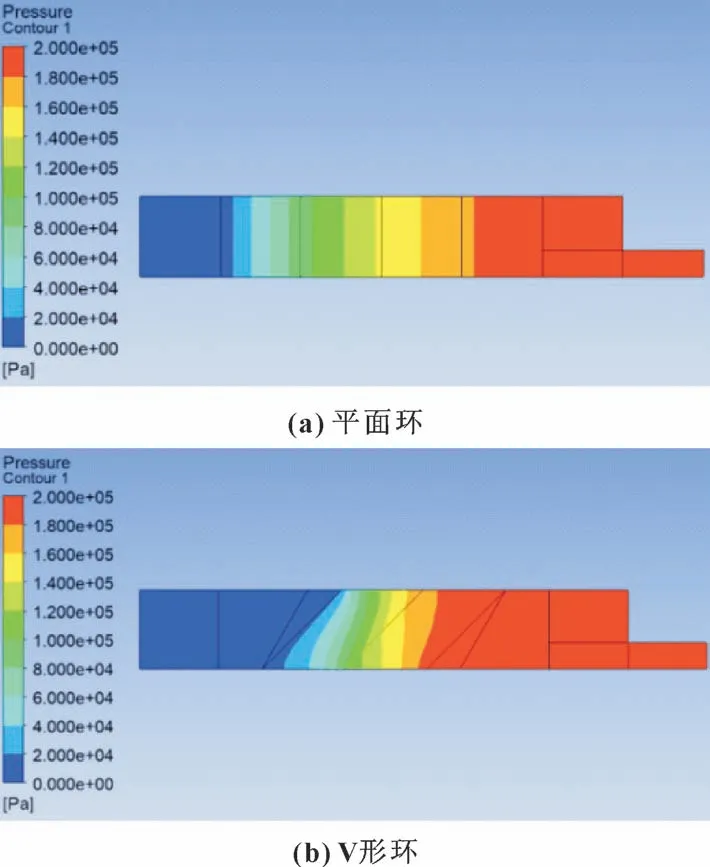
图11 氦气压力分布云图Fig.11 Distribution of helium pressure： （a） planar rings； （b） V type rings

在平面环填料内， 介质压力下降先慢后快， 这是因为距离压盖越近， 填料渗透率越小； 介质在V 形环填料内， 压力下降区域位于主要密封功能环， 即3、 4 环中， 这是因为应力集中现象导致这2 个填料环具有较高的流体阻力。

4 密封性能对比

阀杆填料密封机构运行过程中， 填料被磨损后体积减小， 剩余部分变形程度也越来越小， 渗透率随之增大。 利用1.3 节所述方案得到密封机构经过不同次数机械循环后的受力状态， 分别代入流场模型进行泄漏率计算， 以得到2 种结构的填料组在21 kN 预紧力下的理论密封寿命。

文中分别计算了阀杆外、 内移时的泄漏率， 以平均值作为填料组当前的泄漏率。 根据标准ISO15848—2015[17］（工业阀逸散性泄漏的测量、 试验和鉴定程序） 相关内容来将仿真结果中的介质流量转化为泄漏率， 并判断密封是否失效。

根据上述标准， 27 ℃的条件下， 阀杆直径30 mm 时， 填料组氦气泄漏率超过5.87×10-4Pa·m3／s时说明泄漏率低于C 级密封标准， 视为失效。 图12所示为相同预紧力下机械循环过程中填料组泄漏率变化。 可以看出， 在机械循环进行过程中， 平面环填料组泄漏率的增长明显快于V 形填料组。 在21 kN 的预紧力下， 平面环填料组的理论密封寿命在100 ～150次机械循环之间， V 形填料组则处于600 ～800 次循环之间。

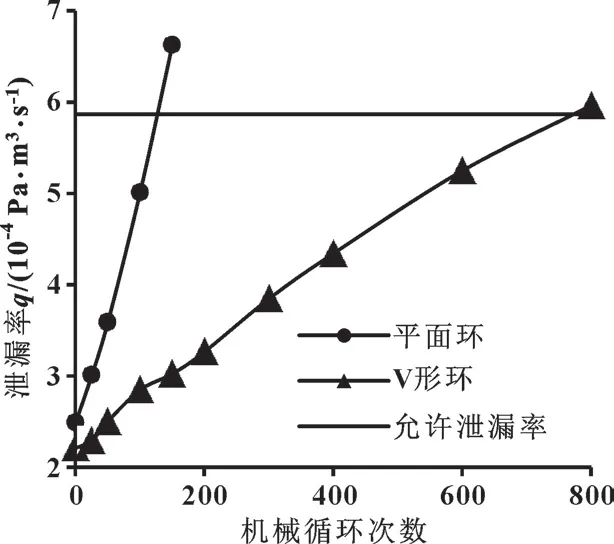
图12 相同预紧力下机械循环过程中填料组泄漏率变化Fig.12 Leak rate of packing seal during the mechanical cycling under same initial pressing force

5 结论与展望

（1） 平面环和优化的V 形环2 种结构的填料组以相同压紧力压紧后， V 形填料组的变形量显著高于平面环填料组， 且由于应力集中现象， V 形填料组内部的应力分布与平面环填料组相比， 位于填料组中间的纯石墨环所受有效应力明显提升。

（2） V 形填料组与阀杆间的摩擦力较低， 即填料磨损速率与设备能耗较低， 利于长时间动密封。

（3） 初始情况下， 阀杆外移时， 平面环填料组密封性能略优， 但内移时， 平面环填料组泄漏率明显更大， 致使初始状态下单周期的平均泄漏率更高。 机构开始运行后， 由于阀杆与平面环填料组之间的摩擦力更大， 致使填料磨损更严重， 最终体现为平面环填料组的密封寿命显著更低。

（4） 在实际情况下， 固定压盖的螺栓会因机构运行产生松动， 导致压盖位置产生微小变化， 而文中在有限元计算的过程中忽略了这一变化。 此外， 文中流场仿真结果为阀杆静止或向单一方向持续运动时机构的泄漏率， 该方法无法得出阀杆改变运动方向的过程中机构的泄漏率。