O 形圈水下吸附状态及脱落现象分析与计算

赵飞虎 许 可 赵国良 齐 新

（1. 中国船舶科学研究中心 江苏无锡 214082； 2. 深海技术科学太湖试验室 江苏无锡 214082；3. 深海载人装备国家重点实验室 江苏无锡 214082）

O 形圈因结构简单、 安装方便、 密封可靠在海洋工程装备中被广泛使用， 如深海充油电机[1］、 水下机器人[2］、 水下滑翔器[3］、 深海液压源[4］、 深海浮游生物取样器[5］、 水下压力补偿器[6］和深海往复动密封结构[7］等。 研究人员已通过仿真、 试验等方法充分验证了O 形圈在深海环境中的密封性能， 但是不同于以上水下装置， 安装在水下启闭舱口盖上的O 形圈不仅要求在关盖状态下保持良好的静密封性能，而且需要在开盖过程中不能因吸附作用而发生脱落现象。

水下启闭舱口盖作为干湿转换系统的关键部件，其性能直接决定了系统能否正常工作。 干湿转换系统简化结构如图1 所示， 由于存在预压缩量， 所以在开盖初始阶段O 形圈不会与密封面发生分离， 从而使舱口盖内部空间增大、 水压降低， 在内外压差的作用下平衡阀孔附近形成水流并流入舱口盖内部空间，在此阶段O 形圈表现为吸附状态。 随着舱口盖进一步开启， 若O 形圈继续被吸附于密封面， 则可能导致O 形圈从密封沟槽内脱落。

图1 干湿转换系统简化结构Fig.1 Simplified structure of wet-dry system

为了避免舱口盖在水下开启过程中发生O 形圈脱落现象， 本文作者以某锥形密封面舱口盖的密封结构为研究对象， 通过有限元仿真、 受力分析、 理论计算以及水下开盖试验的方法， 分析O 形圈在开盖初始阶段吸附状态， 并明确O 形圈脱落的影响因素。

1 有限元仿真分析

1.1 几何模型

由于O 形圈的吸附状态仅发生在开盖初始阶段，并假设在该阶段盖板沿自身回转轴线做直线运动、 不发生偏移， 所以可采用轴对称模型对O 形圈的变形及受力状态进行分析， 其几何模型的外形结构如图2所示。

图2 几何模型外形结构Fig.2 Geometric model shape structure

图中舱口盖密封面圆锥角为60°、d′1为O 形圈安装内径、d2为O 形圈线径、r1表示密封槽棱圆角半径、D表示舱口盖与围壁密封面的间隙值， 并设d1为O 形圈在自由状态下的内径，s为安装时的初始压缩量。 对于锥形密封面处的密封圈目前并没有相关选型标准， 依据文献[8-9］对O 形圈尺寸进行设计。

如图3 所示， 依据表1 参数建立仿真模型， 发现O 形圈与盖板存在着重叠的干涉区域。 为了避免干涉造成的计算收敛性问题， 在仿真分析之前先将盖板沿密封面法向移动一定距离， 待O 形圈与盖板的接触对建立后反向移动盖板恢复至初始位置， 从而保证了O 形圈初始拉伸量及相关参数计算的准确性。

图3 仿真模型预处理Fig.3 Preprocessing of the simulation model

表1 密封结构相关尺寸参数Table 1 Sealing structure size parameters

1.2 材料参数

O 形圈所用橡胶材料为一类超弹性体， 在有限元仿真软件中采用Neo-Hooke 模型、 Mooney-Rivlin 模型、 Yeoh 模型或Ogden 模型等[10-12］作为其本构模型。在使用过程中需要确定模型系数、 泊松比和初始弹性模量， 模型系数一般通过相关文献或软件使用说明确定， 对于橡胶材料泊松比一般在0.45 ～0.499 9 范围内取值[13］， 而初始弹性模量通过对橡胶硬度转换得到。

国际橡胶硬度（IRHD） 与弹性模量的对数在正态分布积分曲线上一一对应[14］， 并且积分曲线在30～80IRHD 范围内两者近似为线性关系[15］。 在该段曲线每隔5IRHD 长度取一个数据点， 并采用最小二乘法对其进行线性拟合。

式中：Hr表示国际橡胶硬度（IRHD）；E0表示初始弹性模量（MPa）。

选取硬度为70IRHD 橡胶作为O 形圈材料， 并以Neo-Hooke （N-H） 模型作为其材料本构模型， 橡胶材料参数见表2。

由于盖板和外壁的材料为高强度钢， 所以其弹性模量远大于O 形圈， 因此以盖板和围壁的密封面为仿真对象并将其设置了刚体模型， 以简化模型提高仿真效率。

1.3 仿真结果及分析

以舱口盖关闭状态为仿真初始状态， 并逐渐开启舱口盖， 忽略此过程中动态因素对O 形圈的影响，采用静力学仿真分析其状态。

假设盖板与围壁分离的过程中， 盖板内侧水压始终小于外侧， 且压差值Δp保持恒定。 若O 形圈与密封面接触点的压力值大于Δp， 则认为密封有效， 两者保持紧密贴合状态； 反之则认为密封失效， 两者分离。 初定压差Δp为20 kPa 进行仿真， 其结果如图4所示。

图4 压差20 kPa 下O 形圈最大接触应力仿真结果Fig.4 Simulation results of maximum contact stress of O-ring under pressure difference of 20 kPa

图中密封面间隙值为1 mm 表示O 形圈的初始压缩量为0， 压差经过密封槽底面作用于密封槽侧面S1以及围壁锥面S2； 间隙值为4.6 mm 表示O 形圈在压差作用下运动至密封槽棱圆角处； 间隙值为7 mm 是O 形圈绕棱圆角转动过程中的某一状态； 间隙值为9.4 mm 表示O 形圈截面中心位于棱圆角中心水平线之下的某一位置， 此时O 形圈内径经过最大值后逐渐开始减小， 即O 形圈已经从密封槽内脱离， 若继续开启舱口盖则会出现O 形圈脱落现象。

在运动过程中O 形圈与密封槽侧面S1 和围壁锥面S2 的最大接触应力值始终大于20 kPa， 并且面S1的最大接触应力值始终保持增长趋势， 而面S2 的最大接触应力值经过先减小再增大的变化阶段。 为了进一步明确压差值与接触应力之间的关系， 减小压差值为5 kPa 再次进行仿真， 其结果如图5 所示。

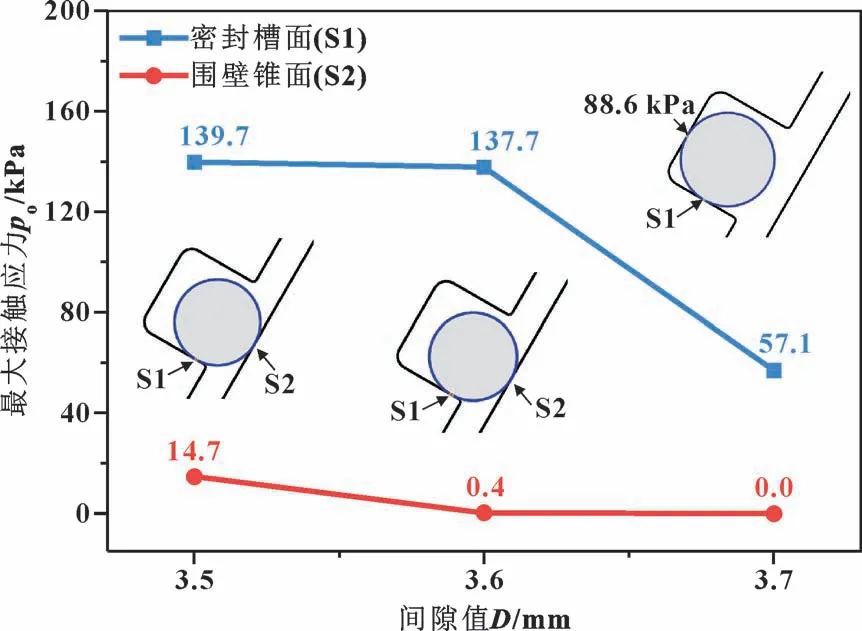
图5 压差5 kPa 下O 形圈最大接触应力仿真结果Fig.5 Simulation results of maximum contact stress of O-ring under pressure difference of 5 kPa

图中间隙为3.5 mm 时面S1 和面S2 的最大接触应力大于5 kPa， 即O 形圈的密封有效； 间隙为3.6 mm 时面S2 处的最大接触应力为0.4 kPa， 小于5 kPa， O 形圈与面S2 分离， 密封圈两侧经过面S2 连通， 密封失效； 间隙值等于3.7 mm 仅表示O 形圈下一个运动状态， 不代表实际值， 此时压差值等于0，O 形圈在自身径向力的作用恢复至初始状态。

通过对比2 次仿真结果， 可以得出以下结论：（1） 只要开盖初始阶段存在压差， 则O 形圈必然会被吸附于密封面上， 并且压差越大吸附状态保持时间越长， 甚至导致O 形圈从密封槽内脱落； （2） 在O形圈吸附移动过程中， 必然存在一个临界位置， 一旦O 形圈移动到该位置则一定会发生脱落， 反之O 形圈恢复至在密封槽中的初始状态； （3） 无论是否发生脱落现象， O 形圈始终与面S1 保持接触， 因此O形圈与面S2 的接触状态是关键分析对象。

2 吸附状态受力分析

在压差值一定的条件下， 若在临界位置处O 形圈与面S2 的最大接触应力等于压差值， 则称该O 形圈的参数为此压差值下的临界参数。 显然依靠有限元仿真方法很难求得临界参数， 因此通过对O 形圈吸附移动过程中受力状态的分析， 推导出临界状态参数的计算公式， 以此确定临界位置与临界参数。

根据上文中有限元仿真分析结果可知， O 形圈在吸附状态时变形量很小， 因此忽略密封圈的微小变形， 以圆形截面为对象、 以圆心O为受力点进行受力分析。 如图6 所示， O 形圈在吸附状态受力分别为压差Δp， 面S1 处的法向支撑力FN1与切向摩擦力f1，面S2 处的法向支撑力FN2与切向摩擦力f2， 以及O 形圈径向力Fr。

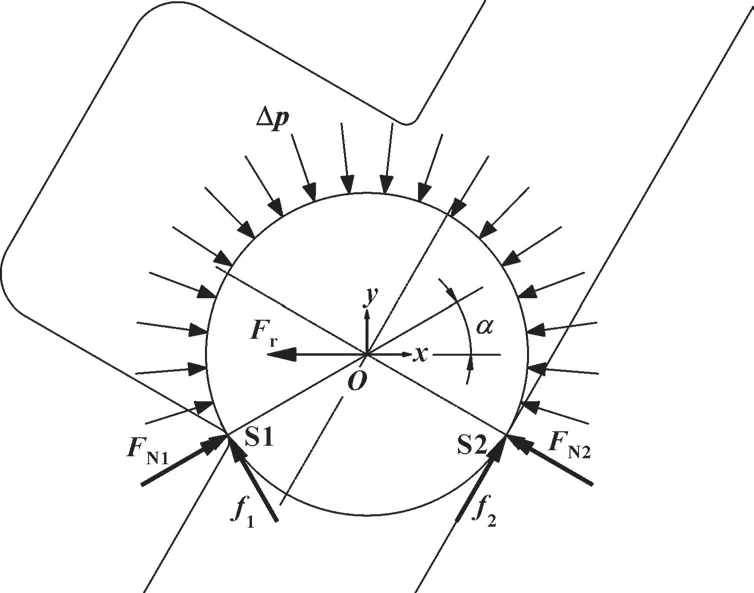
图6 吸附状态受力分析Fig.6 Force analysis to absorbed state

依据力的平衡条件， 以圆心O为对象可得到：

FN1与坐标系x轴正向夹角为α， 且α随着O 形圈的移动而发生改变；FN2与坐标系x轴正向夹角与密封面圆锥角有关， 当圆锥角取60°时， 夹角为150°； 取橡胶与金属的摩擦因数为0.3[16］， 则f1＝0.3FN1、f2＝0.3FN2， 且与x轴正向夹角分别为α＋90°、 150°～90°。

压差Δp的作用范围与接触点的位置有关， 即-30°～α＋180°， 则Δp与x轴正向夹角φ为-30°＋180°～α＋360°， 因此其在x轴与y轴上合力可表示为

单位周长径向力Fr与O 形圈弹性模量E、 线径d2和拉伸量δ有关[17］， 由于O 形圈的变形量很小，所以用初始弹性模量E0代替E， 则单位周长径向力大小可表示为

其中拉伸量δ与密封面间隙值D和O 形圈自由状态内径d1有关， 由于O 形圈的移动过程分为沿密封槽侧面直线移动和绕棱圆角中心转动两段， 所以相应的拉伸量采用分段表示方法：

式中：s≤D≤d2／2-r1， 并且夹角α始终保持为60°； 0°≤α≤60°， 并且α＝60°表示转动的起点，α＝0°表示O 形圈截面中心与棱圆角中心处于同一水平线， 若继续转动则O 形圈必然脱落、 与面S2 分离，吸附状态不存在， 所以对于α＜0°不做分析。

将式（3）、 （4）、 （5） 代入式（2） 中得到包含参数FN1、FN2、 Δp、D、α、r1、d′1、s、d1、d2和E0等的方程组。 按照表1 和表2 对相应参数进行取值，并取Δp＝0、 5、 10、 20 kPa 分别求解FN1和FN2的值，如图7 和图8 所示。

图7 中， 随间隙值的增大法向支撑力FN1曲线呈现为上升趋势，FN1的值随Δp减小整体趋于减小， 但FN1始终大于0。 图8 中， 随间隙值的增大法向支撑力FN2曲线呈先下降再上升的趋势， 最小值在曲线拐点4.6 mm 处， 且随着Δp减小FN2的最小值从大于0向小于0 转变。FN2＜0 表示在该位置O 形圈与面S2发生了分离。 其中间隙值为4.6 mm 对应于α＝60°，即O 形圈转动起点。

图7 不同压差下面S1 的法向支撑力随间隙的变化Fig.7 Variation of normal force of surface S1 with clearance under pressure difference

在转动起点处， 若FN2对应的接触应力值大于Δp， 则在整个开盖初始阶段O 形圈均吸附于面S2，并发生脱落现象； 若对应的接触应力值小于Δp， 表明在此位置之前O 形圈已经与面S2 发生分离， O 形圈不会脱落， 因此说明O 形圈转动起点位置即为临界位置。

在临界位置处， 若FN2对应的接触应力值等于Δp， 则相应O 形圈的参数即称为临界参数。

3 临界参数计算

3.1 最大接触应力值

由于法向支撑力法向支撑力FN2无法与压差Δp直接进行比较， 且吸附状态下O 形圈的变形量十分微小， 所以可以采用赫兹接触公式将FN2转换为相应的最大接触应力值p0。

由于密封面为刚性材料， 所以其弹性模量远大于O 形圈弹性模量； 在O 形圈的圆形截面上密封面为一条30°的直线， 所以其曲率半径趋近于无穷大。 基于这两点将赫兹线接触公式化简为

为保证式（6） 合理性， 分别取硬度60、 70 和80IRHD 的O 形圈进行有限元仿真， 并通过计算与仿真结果对比分析对其进行验证。 按照表1 中O 形圈的相关参数建立1／2 对称仿真模型， 并且为保证计算精度在接触部位细化网格。 如图9 所示。

图9 1／2 对称仿真模型Fig.9 1／2 symmetrical simulation model

固定仿真模型的下平面， 载荷FN2分别取0.1、0.5、 1、 5 和10 N／mm 的1／2 加载于上平面进行仿真， 并提取最大接触应力值。 采用相同的载荷与硬度参数， 代入式（4） 得到最大接触应力计算值， 如图10 所示。

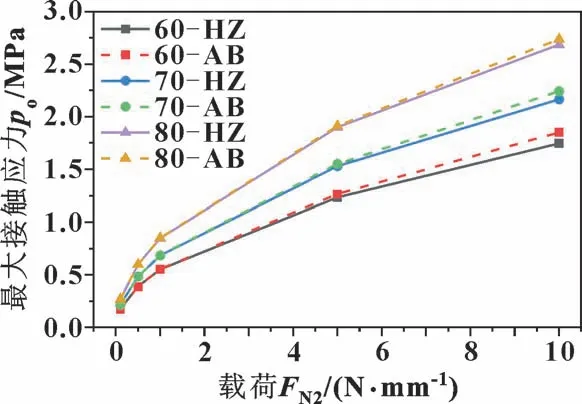
图10 不同橡胶材料硬度时最大接触应力仿真和计算结果比较（HZ 表示赫兹公式计算值， AB 表示仿真结果）Fig.10 Comparison of simulation and calculation results of maximum contact stress under different rubber material hardness（HZ represents the calculation values of Hertz formula， AB represents the simulation results）

图10 中， 60、 70、 80 分别表示橡胶材料硬度值， HZ 表示赫兹公式计算值， AB 表示仿真结果。 在载荷较小时， 相同硬度的2 条曲线基本保持一致， 但随着载荷的增加两者差异逐渐加大； 并且随着材料硬度减小， 2 条曲线的差异程度在逐渐增大。 导致这种现象产生的原因是： 载荷增大或硬度减小， 均使材料的弹性模量减小， O 形圈变形量相应增加， 从而不满足赫兹接触理论应力分布的假设条件。 因此， 在使用赫兹公式计算O 形圈的最大接触应力时应保证其变形量相对较小。 对文中吸附状态下的O 形圈， 其载荷与硬度均符合要求。

3.2 临界参数值

为得到O 形圈临界参数计算公式， 令p0＝Δp、α＝60°， 并将相关计算式代入式（2） 中， 可得到关于参数Δp、E0、d2、d1和s等的方程式：

对于一个干湿转换系统， 其相关结构设计完成后压差Δp即可确定， 因此在分析过程中Δp作为一个常数变量； 对于O 形圈的4 个参数E0、d1、d2和s，通过初步选型设计确定其中任意3 个参数后， 结合方程（7） 即可求解第4 个参数， 该参数即为O 形圈的临界参数值。

由于临界参数值对于计算精度十分敏感， 且方程中包含非线性项， 若计算过程中采用近似值表示三角函数值等常量参数， 则会使计算结果出现较大偏差，因此采用MATLAB 软件编程求解方程的数值解以保证计算结果的准确性。 初定Δp＝5、 10、 20 kPa， 并依次选取不同大小的E0、d1、d2和s进行计算， 以分析O 形圈临界参数值的变化情况， 其中E0采用橡胶硬度Hr表示。

表3 中分别以Hr、d1、d2和s为变量， 计算其在不同压差下的临界参数值。 比较不同变量临界值的相对变化量， 得出对于压差变化的灵敏度从强到弱依次排序为s、d2、Hr、d1； 其中随着Δp增大压缩量s出现了负值， 线径d2已大于O 形圈常规使用尺寸， 显然与工程设计要求不符。 因此， 在O 形圈选型设计中， 将调整内径d1以保证O 形圈不会发生脱落作为第一选择。

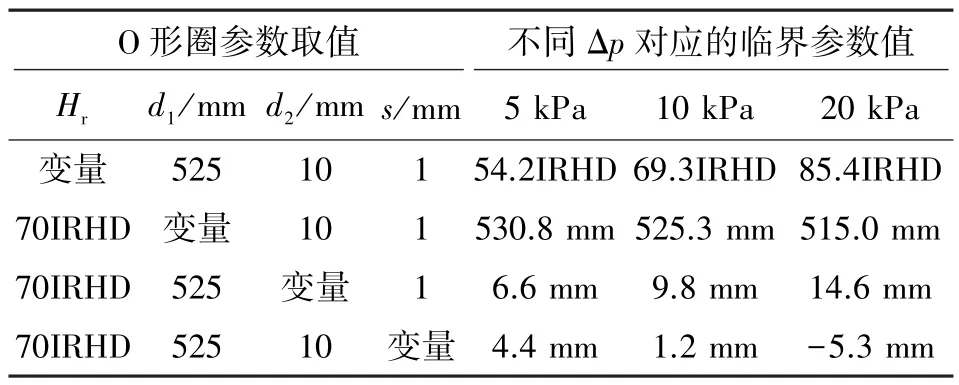
表3 O 形圈不同变量的临界参数值Table 3 Critical parameter values of O-ring with different variables

4 水下开盖试验

为了验证临界参数计算方法的合理性， 基于某型干湿转换系统样机开展水下开盖试验， 舱口盖密封结构相关参数见表1 和表2。 在舱口盖内侧安装深度计， 记录开盖前后深度计数值分别为0.68 和-0.64 m， 则压差Δp＝13.2 kPa， 以内径d1为变量计算得到临界值为521.9 mm。 选取内径d1为525 和515 mm的O 形圈分别安装在盖板密封槽内， 并进行水下开盖试验， 试验装置如图11 所示。

图11 水下开盖试验Fig.11 Cover opening test in water： （a） O-ring installation； （b） O-ring falling off

试验结果表明， 内径525 mm 的O 形圈在开盖后发生脱落现象， 内径515 mm O 形圈的虽然出现了吸附现象， 但并没有脱落。 这在一定程度上验证了计算的临界值是可信的， 临界参数值的计算方法是合理的。 另外， 试验时2 种尺寸的O 形圈在开盖初始阶段均出现了吸附现象， 不同之处在于内径515 mm 的O 形圈的吸附时间相对较短。 这是因为O 形圈的移动距离较小， 与吸附状态仿真结果相符合。

5 结论

采用有限元仿真分析的方法分析开盖初始阶段O形圈在吸附状态下的移动情况， 通过受力分析确定O形圈发生脱落现象的临界位置， 并结合赫兹接触理论提出了临界参数的计算方法。 主要结论如下：

（1） 对于锥形密封面舱口盖， 若水下开盖时O形圈两侧存在压差， 则必然存在吸附状态； 若O 形圈保持吸附状态移动并与密封槽棱圆角接触后， 则开盖后密封圈会发生脱落现象。

（2） 为了避免脱落现象的发生， 在O 形圈选型设计时必须考虑其临界参数， 并根据其数值大小调整O 形圈相关参数。 其中， O 形圈内径参数对压差变化的灵敏度最低， 在设计过程中其临界参数值应作为第一选择。

（3） 虽然橡胶材料是超弹性体， 但是O 形圈在微小变形的条件下， 赫兹接触理论仍然适用， 且理论计算精度与有限元仿真结果基本一致。