Shock response of cyclotetramethylene tetranitramine (HMX) single crystal at elevated temperatures

Kai Ding, Xin-Jie Wang, Zhuo-Ping Duan, Yan-Qing Wu, Feng-Lei Huang

State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing,100081, PR China

Keywords:Plate impact experiment HMX single crystal Elevated temperature Hugoniot elastic limit Thermal hardening behavior

ABSTRACT To investigate the shock response of cyclotetramethylene tetranitramine (HMX) single crystals at elevated temperatures (below the phase transition point), plate impact experiments at elevated temperatures were designed and conducted. The HMX/window interface particle velocities at temperatures of 300 K,373 K,and 423 K were measured by the velocity interferometry system for any reflector(VISAR)technique. To further analyze the related mesoscale deformation mechanisms, a nonlinear thermoelastic-viscoplastic model was developed, which considers thermal activation and phonon drag dislocation slip mechanisms.The proposed model could well reproduce the measured thermal hardening behavior of Hugoniot elastic limit (HEL) of HMX single crystals. At elevated temperatures, the reduced dislocation mobility was observed, which stems from both phonon scattering and radiative damping effects. Comparatively speaking, radiative damping contributes less than phonon scattering to thermal hardening behavior. The calibrated model was further used to predict shock response of HMX single crystals with different thicknesses at different initial temperatures.Both the stress relaxation and elastic precursor decrease with thickness are mainly due to the rapid dislocation generation.These insights shed light on the interplay between dislocation motion and dislocation generation in thermal hardening behavior, stress relaxation, and elastic precursor decay, which serves to reveal the mesoscale deformation mechanisms at elevated temperatures.

1. Introduction

The ignition and initiation of polymer-bonded explosives(PBXs)are always the focus of evaluating its safety and applying its good detonation performance. Cyclotetramethylene tetranitramine(HMX)is a well-known high explosive used as the main component in PBXs. The shock response and mesoscale deformation mechanisms of HMX single crystals subjected to elevated temperatures feature a crucial effect on initiation characteristics of PBXs under extreme conditions (i.e., high temperatures, high pressures and high-strain rates).

A standard means of investigating the shock response of explosive single crystals under high strain rates includes the plate impact test[1-4].For example,a series of plate impact experiments were conducted to measure the shock response of pentaerythritol tetranitrate (PETN) [5-7]. Strong anisotropic elastic-plastic response and impact sensitivity in PETN were noted due to steric hindrance to shear along available slip planes[8].To further study the deformation mechanism of explosive single crystals,Dick et al.[9] investigated dynamic response of the (110), (011), and (010)planes of HMX single crystals perpendicular to the loading axis and observed anisotropy in Hugoniot elastic limit (HEL) and elastic precursor decay. They pointed out that the dislocation-slip based plastic mechanism still played a role in these brittle molecular crystals. In their subsequent research, Hooks et al. [10,11] carried out plate impact experiments on oriented cyclotrimethylene trinitramine (RDX) single crystals at 3 GPa. Besides the anisotropic response observed among the (111), (100), and (210) orientations,wave profiles of three orientations also exhibited elastic precursor decay. Previously, most experimental works on the dynamic mechanical properties of explosive single crystals were performed at room temperature.Considering the complex application scenarios,shock studies of explosive single crystals at elevated temperatures are needed to obtain thermomechanical properties.

Based on the experimental data of dynamic loading, plenty of computational works have been conducted to gain better understanding of deformation mechanisms. Winey and Gupta [12]developed a dislocation model for describing the elastoplastic impact response of PETN single crystals, which contains nonlinear elasticity by using third-order elastic constants. Barton et al. [13]proposed a dislocation-based model for HMX single crystals under high strain rates. The crystals plasticity model considered thermal activation and phonon drag dislocation slip mechanisms. The model parameters were calibrated through detailed experimental results to predict the pore collapse under shock loading. Wu and Huang [14] developed the thermodynamic constitutive model,which includes the pressure and temperature dependence of elastic modulus and the modified equation of state for nonlinear deformation of HMX single crystals.De and coworkers[15]incorporated dislocation generation and motion to explain orientationdependent behavior of α-RDX single crystals. After calibrating against wave profiles of (111) and (210) orientations, they studied the effects of strain rate and phonon drag on the critical resolved shear stress.Luscher et al.[16]also developed a dislocation densitybased model for thermomechanical response of α-RDX and calibrated the model by wave profiles from four orientations of crystals. They presented that rapid dislocation generation is critical to accommodate plastic deformation in these crystals of low initial dislocation density. Wang et al. [17,18] carried out plate impact experiments of HMX and RDX single crystals with different orientations at room temperature and developed a dislocation plasticity model for anisotropic crystals, which can well capture the shock response of single crystals. Based on the anisotropic elastoviscoplasticity model restricted to simple loading conditions such as shock or impact, Wang et al. [19] developed a fully coupled thermomechanical dislocation model for the explosive crystal β-HMX subjected to isentropic compression loading. Contributions of anisotropic temperature rises by pressure volume work and dislocation-based plasticity work influenced by loading history were provided. Then, Wang et al. [20] developed a thermomechanical consistent model,which considers material anisotropy,nonlinear thermoelasticity, dislocation-based plasticity, and shear cracking induced damage. From the perspective of mesoscale deformation mechanism, the interplay and competition between the dislocation activity on ten slip systems and shear cracking on three crack systems were revealed.Plenty of previous constitutive models ignored the temperature dependence of elasticity or dislocation plasticity.It is difficult to predict the shock response of single crystals with different thicknesses at elevated temperatures.Therefore, a temperature-dependent nonlinear elastic-viscoplastic model is needed to reveal the mechanisms of temperaturedependent mesoscale deformation and HEL decay for HMX.

Under various dynamic loading conditions, the experimental configuration of crystal/window was often used to indirectly obtain the shock response of single crystal [9,10,17]. Thus, the interface effect has to be considered in the simulations. Both experimental and numerical techniques have been used to study the effect of interface. Palmer et al. [21] observed that interface was weaker than the bulk material phases in PBXs under tensile loading.Zhuang et al. [22] conducted an experimental investigation of shock wave propagation in periodically layered composites. They compared the Hugoniot data of layered composites with the Hugoniots of their homogeneous component materials and investigated the influence of interface number and interface scattering.It was concluded that the dispersion of shock energy due to the interface had a more dominant effect than the material nonlinearity at lower shock pressures.Prakash et al.[23,24] performed an experimental measurements of interface shock viscosity in hydroxyl-terminated polybutadiene (HTPB)-ammonium perchlorate (AP) material system using mechanical Raman spectroscopy (MRS) combined with laser pulse shock loading. It was observed that shock viscosities of the altered chemical compositions of the interfaces were different. A power law relation was obtained between shock wave rise time and the shock viscosity based on the simulation results.According to the previous research,the shock viscosity of the interface plays an important role in the measurements of the energetic materials under dynamic loading.

Previous shock experiments of single crystal at elevated temperature were performed on inert material [25-27]. Zaretsky and Kanel [28-30] carried out a series of plate impact experiments of face-centered cubic (FCC) metal single crystals at elevated temperatures and observed abnormal thermal hardening behavior.Subsequently, Krasnikov et al. [31] developed a plasticity model considering thermal activation and phonon drag effects.The model could well reproduce the thermal hardening behavior of the shockcompressed aluminum single crystal. They proposed that this behavior is attributed to the viscous drag of dislocations.Gurrutxaga-Lerma et al. [32] utilized dynamic discrete dislocation plasticity model to shed light on deformation and failure mechanisms of metals in the laser-driven shock experiments. They reported that the shock front is relaxed by the shielding due to elastodynamic fields of dislocations. The magnitude of this shielding decays with temperature,which leads to the higher HEL.Austin [33] utilized the dislocation dynamic continuum model to study the effect of temperature on the dynamic behavior of aluminum and compared the simulations with other typical models. Recently, there are many studies on the temperature dependence of the yield strength of metallic crystals under shock loading [34-36]. While the development of constitutive model of shocked explosive single crystals subjected to high temperatures is slow due to no access to related experiments.

In the present paper,the shock response of HMX single crystals at elevated temperatures is investigated through the plate impact experiment. Considering that the β →δ phase transition temperature of HMX single crystals is 435 K[37],we preheat separately the crystals to 373 K and 423 K. To reveal the mesoscale deformation mechanisms, a nonlinear thermoelastic-viscoplastic model for HMX single crystals is developed. The model is calibrated through experimental results to obtain the related mesoscale parameters.The developed model is employed to analyze the thermomechanical response of HMX single crystals under shock loading at different initial temperatures. Dislocation generation and mobility are analyzed to unravel the mechanism of thermal hardening. The effects of phonon scattering and radiative damping are quantified to better understand the evolution of the dynamic yield point with temperature.The temperature rise induced by the pressure volume work and dislocation-based plasticity work is calculated to analyze the thermodynamic response of shock-compressed HMX single crystals at elevated temperatures. Shock response of HMX single crystals with different thicknesses at different initial temperatures are predicted to evaluate its safety.

The remainder of paper is organized as follows. Experimental techniques and results are summarized in Section 2. A thermomechanical dislocation model and computational models of loading on HMX single crystals are provided in Section 3. Simulation results and discussion are presented in Section 4 followed by conclusions in Section 5.

2. Experiment

2.1. Sample preparation

HMX usually exhibits four polymorphs,i.e.,α,β,γ,and δ[38]and β-HMX is the most stable polymorph [39]. Therefore, all the HMX single crystals used in experiments were in the β phase, and they were obtained by cutting the large pure single crystals grown and recrystallized by using acetone-solvent slow evaporation method.

Before the experiment, it is necessary to ensure that the machined surfaces of HMX single crystals are free of defects. As shown in Fig. 1, the mesoscopic characteristics of the machined surface of single crystals at 50 and 200 times magnification were observed with a microscope to ensure quality, respectively. In addition,orientations of all crystals were(011)determined by X-ray diffraction (XRD) experiments to ensure the consistency of the crystal orientation used in the experiments and avoid the influence of anisotropy induced by different crystal orientations.

2.2. Target assembly

A multi-groove aluminum structure was designed as displayed in Fig. 2. A heating resistance wire was wound in the groove and was connected in circuit.HMX single crystal was mounted between a φ 20 mm,4 mm-thick z-cut quartz anvil and a ∅20 mm, 4 mmthick lithium fluoride (LiF) window. A thermocouple was fixed in the keyway to measure the lateral temperature of the HMX single crystal,which subsequently fed back to a temperature controller to achieve a steady temperature.A high temperature resistant silicone elastomer was utilized as adhesive to mount the HMX single crystal to the anvil, the thermocouple to the HMX single crystal, and the window to the HMX single crystal. VISAR system was used to measure HMX/LiF interface particle velocity. The surface of the window adjacent to the crystal was coated with a~1 μm aluminum mirror for VISAR system to strengthen reflection intensity.

2.3. Experiment setup

The designed heating device was used to preheat the HMX single crystals to the temperature of 373 K and 423 K.Plate impact experiments of HMX single crystals were conducted on a φ57 mm single-stage gas gun. The flyer velocity was measured by metal probe.Shorting pins were arranged at the end of the barrel.When the projectile came out of the muzzle, a trigger signal was sent to the oscilloscope via a synchronizer. The photoelectric switch was then triggered after~330 μs.The delay time was determined by the estimated impact velocity and the distance between the pin and impact surface. After the photoelectric switch was turned on, the VISAR recorded particle velocity at the crystal/window interface and outputted the signal to the oscilloscope. Fig. 3 shows the schematic diagram of the configuration and layout of the target chamber.The ∅53 mm 8 mm-thick 2024 Al flyer was launched in the gas gun to reach a shock pressure of ~2.7 GPa until the flyer impacted the target assembly. A turning mirror and a positioner were used to deflect the laser path by 90°, which avoids the laser probe to be damaged by impact while ensuring the measurement accuracy.

2.4. Wave profiles

Fig. 4 illustrates HMX/LiF interface particle velocity profiles at elevated temperatures. The wave profiles exhibited a distinct elastic-plastic double wave structure. From the wave profiles, the elastic wave first propagated to the interface, particle velocity jumped and the elastic precursor appeared. Subsequently stress relaxation occurred. Finally, the plastic wave propagated to the interface, and particle velocity increased sharply to the final plateau.

Fig.1. Microscopic morphologies of HMX single crystal at (a) a low magnification and (b) a high magnification.

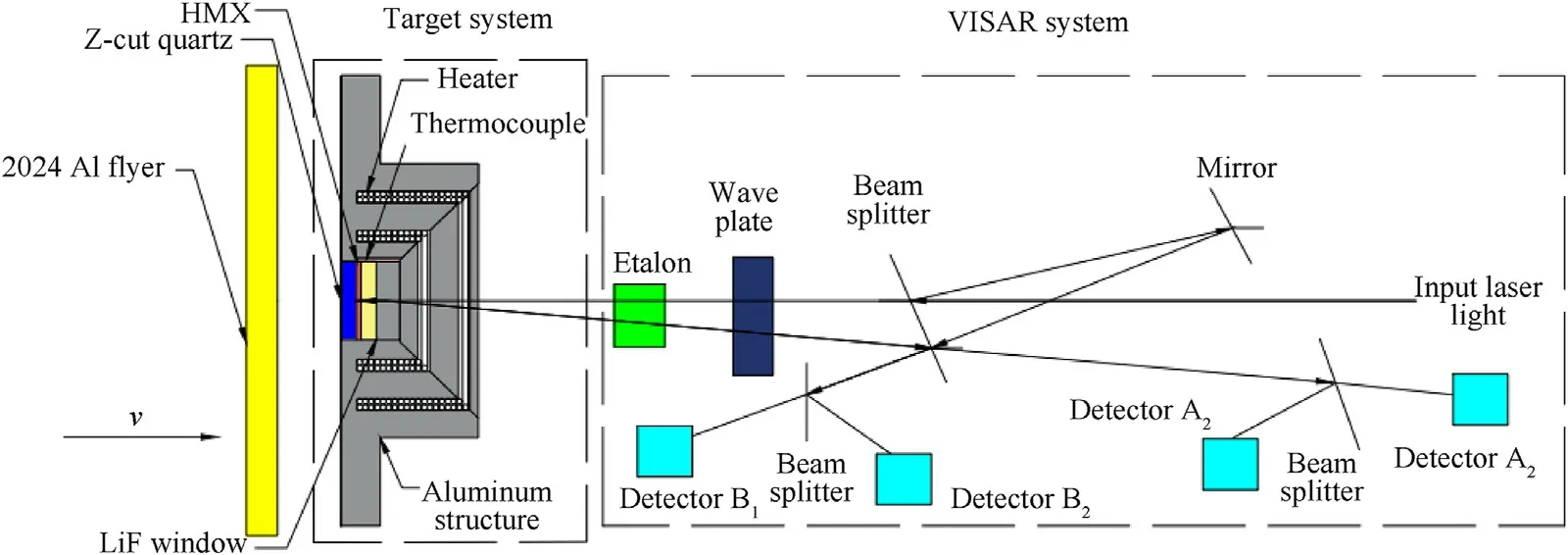
Fig. 2. Schema of the plate impact experiment with VISAR system.

Fig. 3. (a) Light gas gun system and (b) Target chamber.

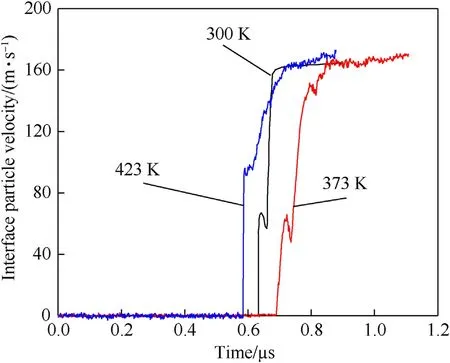
Fig. 4. HMX/LiF interface particle velocity profiles at elevated temperatures.

The particle velocity corresponding to the first peak at elevated temperatures is the interface particle velocity corresponding to HEL. According to the acoustic impedance matching method, the in-situ shock physical quantities of the HMX single crystal at 300 K from Ref. [17] were converted to the data of HMX/LiF interface. A detailed conversion is presented in Ref. [40]. Compared with a particle velocity of 67 m/s at 300 K,HEL at 373 K corresponded to a particle velocity of 65 m/s.At 423 K, the interface particle velocity corresponding to HEL abnormally intensified to 95 m/s, exhibiting thermal hardening behavior.Table 1 presents experimental results of HMX single crystals at different initial temperatures, including initial temperature Tinitial,single crystal thickness h,flyer velocity v,interface particle velocity uelintcorresponding to HEL, and interface particle velocitycorresponding to the final plateau. There islittle difference of the final interface particle velocity with temperature as listed in Table 1.

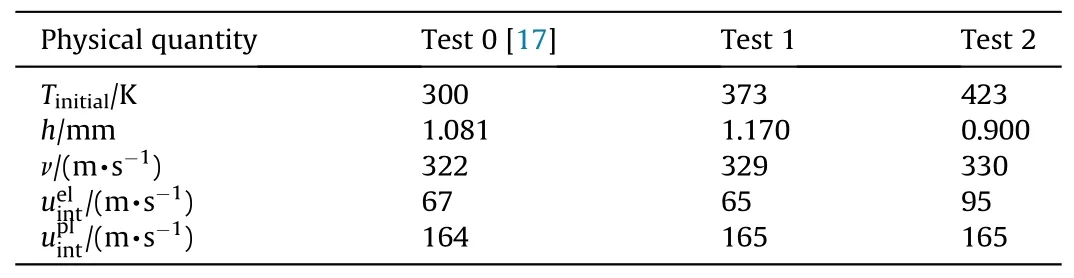
Table 1 Experimental results of(011)oriented HMX single crystals at elevated temperatures.

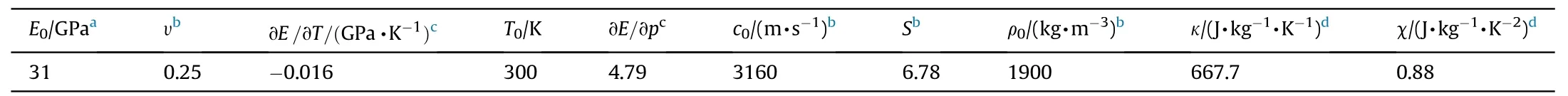
Table 2 Parameters for thermoelasticity model.

3. Constitutive and computational model

Based on the dislocation model of Austin and Mcdowell [41], a thermomechanical dislocation model for HMX single crystals subjected to high strain rates and high temperatures is developed,including nonlinear thermoelasticity, thermal activation and phonon drag dislocation based viscoplasticity.

3.1. Thermoelasticity

From generalized Hooke's law, the constitutive model is expressed as,

where σ is the Cauchy stress tensor,is the Lame′parameter, εeV=І :εeis the volumetric part of the elastic strain tensor εe,І is the second order identity tensor,andis the shear modulus where E and υ are the elastic modulus and Poisson's ratio, respectively. The pressure- and temperature-dependence of the elastic modulus is incorporated using the relation of Steinberg et al. [42]. Thus, the elastic modulus is written using a first-order Taylor series expansion, i.e.,

where E0is the elastic modulus at ambient temperature T0,p is the hydrostatic pressure, and θ=V/V0is the relative volume.

For shock-loading problems,the mechanical response is usually decomposed into deviatoric and volumetric components. To describe the nonlinear elastic response under high pressures, the volumetric component is usually replaced by an equation of state(EOS) as,

where ρ0denotes the initial density,c0is the bulk sound speed,η=1-θ is the nominal volumetric compressive strain, and S is the slope of the linear relationship between the shock wave velocity D and the particle velocity u behind wave front. The specific heat at constant volume is written using a linearly increasing function of temperature as,

where κ and χ are fitting coefficients. Thermoelasticity model parameters are listed in Table 2.

Table 3 Parameters for flyer and target materials.

3.2. Dislocation-based plasticity

To incorporate the plastic constitutive model based on dislocation motion,the resolved shear stress can be expressed as [47],

The relationship between plastic deformation and dislocation motion subjected to shock loading can be described by Orowan equation [48]. Therefore, the plastic shear strain rate can be given as,

where b is the Burgers vector,ρmis the mobile dislocation density andis the average dislocation velocity.

Dislocation motion and generation are the core processes of crystal slip deformation. The dislocation slip resistance is derived from short-range and long-range obstacles [41]. The former is induced by the interaction of dislocations.Thermal fluctuations can provide the energy necessary to assist dislocations in overcoming short-range obstacle.Hence,the dislocation motion is controlled by the thermally activated regime. The latter is provided by the dislocations, precipitates, and grain boundaries. Here, the dislocation motion is mainly dominated by the phonon drag regime [49].When both thermal activation and phonon drag regime are considered, the average dislocation velocity can be expressed as[41],

where L is the mean spacing between obstacles,tris the transit time between obstacles and twis the waiting time for dislocations to be thermally activated [41],

where υGis the attempt frequency of a dislocation waiting at an obstacle, k is the Boltzmann constant, T is the temperature in the wave front and ΔG is the stress-dependent free enthalpy of activation [50],

where g0is a material constant, p and q are parameters that determine the obstacles distribution[51],and τ0is the mechanical threshold stress. The transit time can be expressed aswhereis the average slip velocity[50],

where B is the temperature-dependent phonon drag coefficient and τeff=τ-τμis the effective shear stress.τμserves as the athermal threshold stress below which there is no viscoplastic flow. For the range τμ<τ<τ0, the dislocation slip regime is the thermal activation. For τ>τ0, the dislocation slip regime is the phonon drag.

Considering the effects of phonon scattering and radiative damping on the average slip velocity,the phonon drag coefficient is defined as [41],

where B0is the phonon scattering coefficient andis the transverse wave speed, where ρ is the current density at the hydrostatic pressure p. The drag-limited slip kinetics depend on the phonon scattering coefficient B0and the transverse wave speed cs.A more general form is adopted to describe B0[33],

where BTand Tmare normalization factors and akare fitting coefficients.

According to the Taylor relation [52], the mechanical threshold stress is assumed as [41],

where τp0denotes the glide resistance of obstacles at 0 K,α0is the dislocation interaction parameter, and ρtis the total dislocation density.Moreover,the athermal threshold stress is written as[41],

where β0is a constant and μ0is the shear modulus at 0 K.

Strain hardening is related to dislocation density, which is composed of mobile and immobile parts.Following the assumption of Winey and Gupta[53],the mobile dislocation density ρmis some fraction f of the total dislocation density ρt, where

where H is a hardening constant and γpdenotes the accumulated plastic shear strain.

To further describe the evolution of mobile dislocation, growth of existing loops and heterogeneous nucleation of dislocation loops are mainly considered [54], where dislocation immobilization caused by obstacles and dislocation annihilation induced by two dislocation with opposite signs can be neglected in many cases due to the context of typically low dislocation densities for molecular crystals [16]. At low shear stresses, dislocations undergo regenerative multiplication via a multiple cross glide mechanism [48]. At higher shear stresses, the stress concentrations will induce dislocation nucleation. Therefore, dislocation generation under large shear stresses is attributed not only to multiplication but also to heterogeneous nucleation[55].Then the mobile dislocation density rate is expressed as [33,53],

where αmultis a multiplication parameter, αnuclis a nucleation parameter, A is threshold stress coefficient, and ˙τ is the resolved shear stress rate.

For the sake of simplicity of suitable candidate systems for plastic slip in β-HMX, the J2flow theory with pure isotropic hardening is utilized to characterize the plastic deformation of crystals.Therefore,the plastic strain rate ˙εpcan be expressed as,

Considering the pressure volume work and dislocation-based plasticity work are heating sources, the heating rate ˙T is calculated as,

3.3. Finite element models

In accordance with the experimental configuration, twodimensional finite element models were constructed using fournode bilinear reduced integral element (CPE4R) to mimic the uniaxial strain condition as displayed in Fig. 5. The 8 mm × 20 mm 2024 Al flyer is partitioned to 800 elements.The 4 mm×20 mm zcut quartz anvil and LiF window are partitioned to 500 and 400 elements, respectively. The HMX single crystals are resolved with the mesh size of 0.005 mm. Through the mesh dependence analysis,this mesh density is sufficient to resolved the model.

Fig. 5. Two-dimensional finite element model.

The surface-to-surface contact algorithm was set up between flyer and anvil, between anvil and single crystal, and between single crystal and window.All the lateral faces were constrained by tying and the back surface of LiF window was maintained traction free. The constitutive of HMX single crystal was defined by a user subroutine to define material behavior(VUMAT).The 2024 Al flyer,z-cut quartz anvil, and LiF window were specified with the Mie-

3.4. Numerical implementation

The proposed model is implemented as the VUMAT into the Abaqus/Explicit finite element code. Fig. 8 plots its computational flowchart. The constitutive model is integrated in time step Δt as follows. A trial elastic stress is expressed as,Grünesien EOS. The D-u relation of the z-cut quartz anvil and LiF window at 423 K were estimated by Christoffel determinants[57,58]and the Hugoniot curve[59,60],respectively.The difference of the longitudinal stresses for the z-cut quartz at 423 K calculated separately by the D-u relation of 300 K and 423 K was about 1.5%.For the LiF window,the calculated difference of those was less than 6%. Moreover, according to the acoustic impedance matching method,the calculated difference of the HELs for the HMX at 423 K was less than 4%.Therefore,the role of temperature in the behavior of z-cut quartz anvil and LiF window was ignored. The EOS parameters at 300 K are summarized in Table 3. To avoid numerical oscillation,the linear volumetric viscosity parameter was chosen as 0.15. The flyer was imposed initially with the velocity listed in Table 1 and the ambient temperature of the single crystal was set separately to the initial temperature of 300 K, 373 K, and 423 K.

Table 4 The material properties with Prony series parameters for Estane 5703:Gi (in MPa)[63].

Considering the effect of shock viscosity of the interface on the shock propagation [23,24,61], the HMX/LiF interface should be modeled in the simulations. Due to the lack of the constitutive model parameters for the HMX/LiF interface,the HMX/LiF interface was modeled by using a 2 μm viscoelastic elastomer glue layer(Estane 5703) to characterize the rate dependent mechanical behavior. The Prony series parameters for Estane 5703 are summarized in Table 4, which were calibrated based on the experimental stress-strain curves of Ref. [62]. Finite element model was displayed in Fig. 6 (a).By varying the number of elements of HMX and LiF, keeping 5 elements in the interface region, an average mesh size of 0.8 μm was chosen for the bulk HMX and LiF to ensure the results independent of the mesh size as shown in Fig. 6 (b).Then the mesh sensitivity of the interface region was illustrated in Fig. 7. The results were translated to better compare the wave profiles with different mesh sizes.In addition,the particle velocity without the interface was compared with that of different mesh sizes along the interface thickness.It was observed that the role of the interface is to decrease the HEL and delay the shock stress to reach its HEL.Note that the stiffness of Estane 5703 obtained from the experimental stress-strain curves of Ref. 62 is less than that of HTPB/HMX interface [61]. Therefore, the HEL attenuation with Estane 5703 is greater than that of HTPB/HMX interface with the assumed density. In terms of the degree of the particle velocity attenuation corresponding to the HEL with Estane 5703, the effect of the HMX/LiF interface could be ignored.

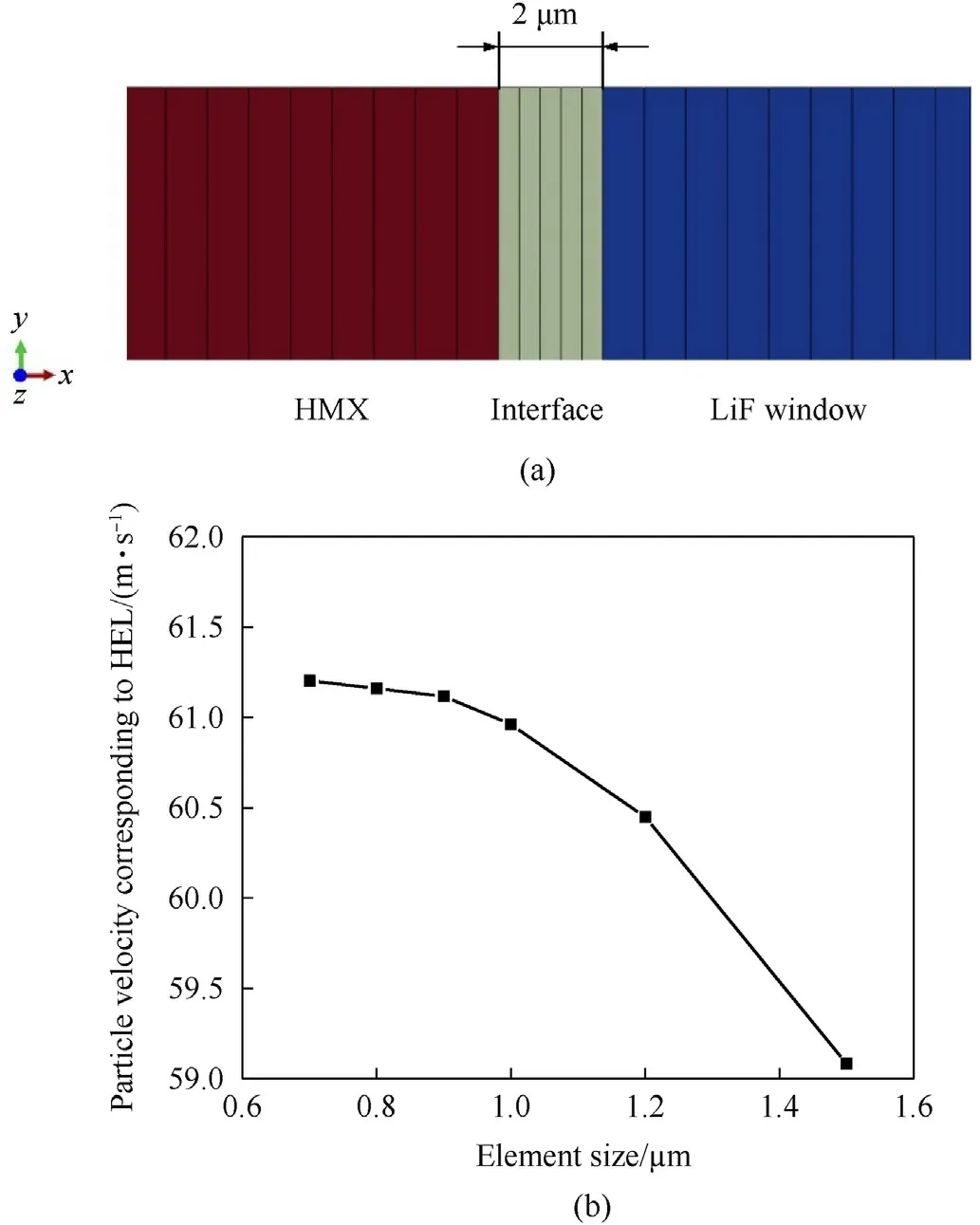
Fig. 6. (a) Finite element model and (b) mesh convergence analysis for Test 1.

Fig. 7. Comparison of the particle velocity without the interface and with different mesh sizes along the interface thickness for Test 1.

Fig. 8. Computational flowchart.

where tr (Δε) denotes the trace of the matrix Δε and Δε is a given strain increment tensor at the beginning of the increment step.Then the deviatoric part of trial elastic stress is written as,

The resolved shear stress is computed using Eq. (6),

Solving the quadratic equation that is obtained by substituting Eq. (12) into Eq. (11) leads to

where

where the transverse wave speed is expressed as cs|t+Δt =The stress-dependent free enthalpy of activation shown in Eq. (10) is updated as,

The average dislocation velocity given in Eq.(8)is calculated as,

The plastic shear strain rate is given as follows,

According to Eqs. (18) and (29), the plastic strain increment is written as,

with the EOS term replaced by a second-order Mie-Grüneisen EOS,the elastic stress is expressed as,

The temperature increment is derived using Eq.(19)as follows,

3.5. Parameters calibration

The magnitude of the Burgers vector b is measured as 7.1332 × 10-10m [69]. Based on the two observed slip systems in space group P21/n for β-HMX,namely,(001)[100]and(101)[101],the Schmid factors for the shocked (011) orientation are 0 and 0.327,respectively[9].Therefore,only the(101)[101（)]is activated and the Schmid factor Z is taken as 0.327.Mean barrier spacingis assumed to be 10|b|[16].Attempt frequency υGis set as 4×1010s-1,material constant g0is chosen as 0.3,thermal activation parameters p and q determining the shape of the obstacle are respectively estimated as 0.5 and 2,dislocation interaction parameter α0is given as 0.5, and proportionality constant β0is evaluated as 0.7 [41].Other plasticity parameters are optimized by model parameter sensitivity as shown in Fig. 9. The parameters for dislocation plasticity model are given in Table 5. Among the seven plasticity parameters, initial mobile dislocation density ρm0is related to the method of crystal growth and is assumed as 1×1010m-2[18].The other six parameters B0,τp0,H,αmult,αnucl,and A are tuned through maximizing the agreement comparing the calculated and experimental wave profiles. Moreover, according to Peierls-Nabbaro stresses of a number of slip systems in β-HMX at 0 K calculated by molecular dynamics simulations [70,71], intrinsic lattice resistance τp0is evaluated at 50-200 MPa. As shown in the figure,magnifying B0,τp0,and H brings higher HEL,while increasing αmultαnucl, A, and ρm0provides lower HEL as displayed in Fig. 9. According to theoretical analysis, when the changes of related parameters restrain dislocation motion or generation, the resolved shear stress is hardly relaxed, thus corresponding to higher HEL.However,when changing related parameters facilitates dislocation generation, the resolved shear stress is attenuated to lower HEL.

Table 5 Dislocation plasticity Parameters for HMX single crystals.

4. Results and discussion

To better compare the wave profiles at different initial temperatures,the experimental and calculated HMX/LiF interface particle velocity at 373 K and 423 K were translated to the right by 0.15 μs and 0.5 μs as displayed in Fig. 10, respectively. As shown in the figure, the calculated distinct elastic-plastic double wave profiles agree well with experimental results.For shock at 300 K,the arrival of plastic wave is well captured, but the amplitude of calculated HEL is slightly lower than that of experimental result. This is ascribed to the promoted dislocation motion or generation. For shock at 373 K, it is clear from the profiles that the calculated distinct elastoplastic double wave structure including the HEL,stress relaxation,and the arrival of plastic wave is quite consistent with experimental results. The calculated HEL of 423 K is in good agreement with the experimental results,but the subsequent stress relaxation is more obvious, indicating that the relaxation rate is higher. The model can well reproduce the thermal hardening behavior of HMX single crystals at elevated temperatures.

4.1. Mechanism of thermal hardening

In the process of uniaxial compression,the resolved shear stress leads to plastic deformation of the single crystal, which in turn relaxes the stress [34]. To demonstrate the relation between resolved shear stress and relaxation rate, Fig.11 plots evolution of the resolved shear stress τ with the plastic shear strain rate ˙γpat different initial temperatures.As shown in the figure,the resolved shear stresses first increase,which facilitates the increase of plastic shear strain rate, while the plastic deformation in turn relaxes the resolved shear stress. Thus, the resolved shear stresses decrease and the spikes occur.Obviously,the spike corresponding to the HEL increases with temperature, but the corresponding plastic shear strain rate decreases. According to Eq. (7), the change of plastic shear strain rate is determined by dislocation generation and dislocation motion.In the following part,we investigate the effects of growth and glide of dislocation separately.

To analyze the effect of dislocation generation on thermal hardening behavior, Fig.12 (a) and (b) plot the mobile dislocation density histories and athermal threshold stress histories at the interface under different initial temperatures. In the model, two dislocation generation mechanisms are considered, namely the growth of existing dislocation loops and the nucleation of new dislocations. Therefore, when the resolved shear stress τ reaches the athermal threshold stress τμ, dislocation slip initiates and accumulates. From Fig. 12 (a), the mobile dislocation densities corresponding to HELs at 300 K,373 K,and 423 K are 3.40×1010m-2,4.52 × 1010m-2, and 4.80 × 1010m-2, respectively. With the increase of ρmHEL,the plastic shear strain rate will magnify as given in Eq.(7).According to the relation between resolved shear stress and relaxation rate mentioned before, the corresponding HEL will decrease. However, HEL shows the thermal hardening behavior,indicating that the thermal hardening behavior is not caused by the temperature dependence of dislocation generation.

In addition,τμexhibits the trend of decrease with temperature as illustrated in Fig.12 (b). Therefore, it can be seen from Eq. (15)that the decrease of the shear modulus is greater than the increase of the mobile dislocation density with temperature.Also,the mechanical threshold stress τ0decreases according to Eq.(14).For the thermal softening of the threshold stress τμand τ0,dislocation slip is easier to be thermally activated,and it is easier to transform from the thermally activated regime to the phonon drag regime.Hence,the temperature dependence of shear modulus determines the threshold stress,which affects the transition of dislocation slip regime.

Fig. 9. Analysis of model parameter sensitivity for Test 1.

Fig.10. Comparison of experimental and calculated HMX/LiF interface particle velocity profiles at different initial temperatures.

Fig.11. Relationship between resolved shear stress τ and plastic shear strain rate ˙γp at different initial temperatures.

To further study the mechanism of thermal hardening from the perspective of dislocation motion, Fig. 13 presents average dislocation velocity histories and resolved shear stress histories at the interface under different initial temperatures. As shown in Fig.13(a),before the plastic wave reaches the interface,the average dislocation velocity is zero. With the arrival of plastic wave, the average dislocation velocity increases sharply. After rising to the maximum, the average dislocation velocity is reduced due to the dislocation multiplication and interaction, which leads to stress relaxation. As the plastic wave propagates, the average dislocation velocity increases. Since the mobile dislocation density grows up continuously, the average dislocation velocity decreases again. It can be seen from Fig.13 (b) that the final resolved shear stress is lower than the corresponding athermal threshold stress τμdisplayed in Fig.12(b).Consequently,the average dislocation velocity is reduced to zero.As the temperature rises from 300 K to 423 K,the overall of the average dislocation velocity decreases, and the first spike decays from 2237 m/s to 1537 m/s.

As shown in Fig. 13 (b), the resolved shear stress sharply intensifies due to the arrival of the elastic wave. Then, the plastic wave propagates to the interface. The resolved shear stress keeps increasing, resulting in a great quantity of mobile dislocations and higher average dislocation velocity. According to Eq. (7), a high plastic shear strain rate occurs, which implies the resolved shear stress begins to be relaxed.With the further propagation of plastic wave, the resolved shear stress increases again. Similarly, the plastic shear strain rate increases because of growth of the mobile dislocations, which induces the attenuation of the resolved shear stress again. The maximum resolved shear stress increases with temperature. Moreover, both the maximum average dislocation velocity and athermal threshold stress τμdecay.It can be seen fromthat the increase of the phonon drag coefficient B exceeds the decay of the average dislocation velocity. As a result,the magnitude of the shear stress is determined by the temperature dependence of the phonon drag coefficient B. The thermal hardening behavior of HMX single crystals is related to the increase of phonon drag coefficient with temperature.The higher phonon drag coefficient strengthens the viscous friction of mobile dislocation,which leads to the decrease of the average dislocation velocity.The reduced mobility of dislocations at higher initial temperatures results in slower plastic shear strain rate and higher flow stress.

The increase of the phonon drag coefficient B with temperature stems from the temperature dependence of the phonon scattering coefficient B0and shear modulus μ. Thus the thermal hardening behavior of HEL essentially results from the dislocation motion controlled by phonon scattering and radiative damping.To quantify the influence of phonon scattering and radiative damping on thermal hardening behavior, the model sensitivities to phonon scattering and radiative damping are obtained as plotted in Fig.14.The amplification factor is defined as the HEL divided by that of the baseline at 300 K.In this temperature range,similar amplifications of HEL are calculated independently by phonon scattering,radiative damping, and their combined effect. Obviously, the phonon scattering and the radiative damping effect are elevated as the temperature increases.However,the contribution of radiative damping to the thermal hardening behavior is less than that of phonon scattering because the shear modulus changes slightly in this temperature range.

Fig.12. (a) Mobile dislocation density histories and (b) athermal threshold stress histories at the interface under different initial temperatures.

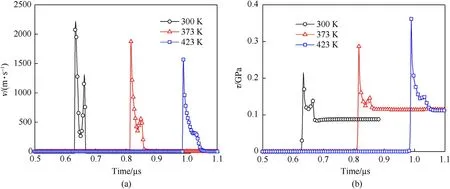
Fig.13. (a) Average dislocation velocity histories and (b) resolved shear stress histories at the interface under different initial temperatures.

Fig. 14. The HEL amplifications provided separately by phonon scattering, radiative damping, and their combined effect at different initial temperatures.

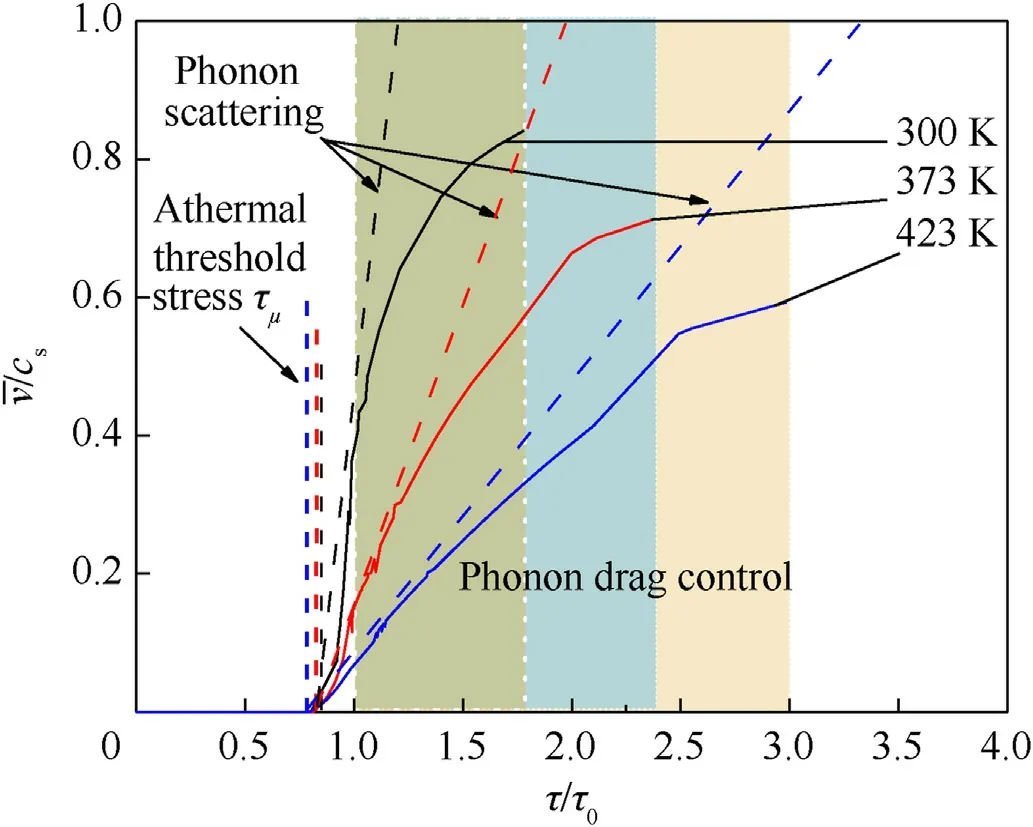
Fig.15. Relationship between /cs and τ/τ0 at different initial temperatures.

Fig.16. (a)Interface longitudinal stress-s11 histories at different initial temperatures and(b)interface longitudinal stress histories with a distance of 0.225,0.45,0.675,and 0.9 mm at elevated temperature of 423 K.

4.2. Evolution of dislocation slip regime

A schematic of the mobility relation is depicted in Fig.15,where the average dislocation velocity and the resolved shear stress have been normalized by the transverse wave speed and the mechanical threshold stress, respectively. In the range τμ<τ<τ0, the growth rate of the average dislocation velocity is higher,which is related to an exponential form of the thermally activated slip. When the resolved shear stress exceeds τ0,the dislocation slip is governed by phonon drag regime.Here,the growth rate is relatively moderated due to attenuation of assistance of thermal fluctuations.For τ/τ0<1,the temperature increments enlarge the region occupied by the thermal activation, but the growth rate of the average dislocation velocity decreases with temperature. This occurs because the phonon scattering coefficient B0increases with the temperature,which leads to the decay of slopes of the phonon scattering lines at the different initial temperatures as shown in figure.Consequently,the higher resolved shear stresses are needed to achieve a given level of. Forτ/τ0>1, the temperature increments magnify the region governed by the phonon drag.Additionally,the growth rate of the average dislocation velocity decreases with temperature.Besides the reason that the increase of B0strengthens the phonon scattering effect, another reason is that as the average dislocation velocity approaches closely the transverse wave speed, the radiative damping becomes stronger due to the reduced the transverse wave speed with temperature.Therefore,the resolved shear stress required to maintain this velocity is increased.

4.3. Thermodynamic response

Fig. 16 (a) plots the interface longitudinal stress histories at different initial temperatures. The dynamic yield limits at 300 K,373 K, and 423 K are 0.904 GPa, 1.529 GPa, and 1.722 GPa. In addition, there is little difference in the final longitudinal stresses with temperature, indicating that the final longitudinal stress is temperature-independent.To further study the response,Fig.16(b)shows the interface longitudinal stress histories at a distance of 0.225 mm,0.45 mm,0.675 mm,and 0.9 mm at 423 K.As the shock wave propagates into HMX single crystal, elastic and plastic wave are separately generated and subsequently propagates in HMX single crystal. Since the elastic wave decays as it propagates, the dynamic yield limit gradually decreases. When the elastic wave reaches the HMX/LiF interface, the dynamic yield limit suddenly increases due to the reflection of the elastic wave.

Both pressure volume work and dislocation-based plasticity work contribute to the temperature rise of shock-compressed HMX single crystal. When the stress is high, it directly causes a higher temperature increase.Interface temperature increment histories at different initial temperatures are displayed in Fig.17. As expected,the temperature rises corresponding to HELs increase with temperature. Moreover, corresponding temperature rises are temperature-independent due to the similar loading pressure.

Fig.17. Interface temperature increment histories at different initial temperatures.

4.4. HEL decay

Fig.18 presents the calculated HMX/LiF interface wave profiles with a thickness of 0.5, 1.0, 2.0, and 3.0 mm at different initial temperatures.As the thickness increases,the rapid stress relaxation is attenuated and eventually the spike disappears.This is similar to attenuation of the stress relaxation of the simulations with decrease of temperature as shown in Fig. 10. From Fig. 11, stress relaxation at elevated temperature begins at a lower plastic shear strain rate. However, the relaxation process at elevated temperature integrally corresponds to the higher plastic shear strain rate,which facilitates the fast stress relaxation. Similarly, reducing the thickness enlarges the corresponding the plastic shear strain rate as plotted in Fig.19(a).This plastic relaxation is induced either via the glide of dislocation or by increasing the mobile dislocation density.It is notable that the stress relaxation is usually accompanied with decay of dislocation mobility. Therefore, the rapid increase in dislocation generation is required to maintain the high plastic shear strain rate as shown in Fig.19 (b).

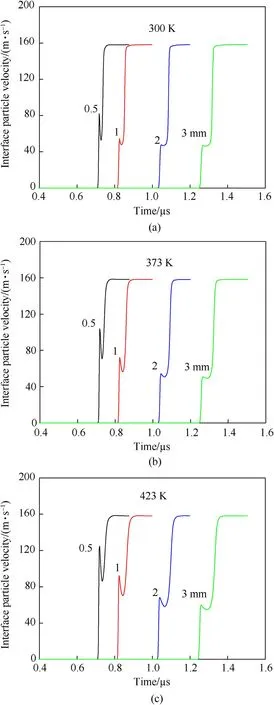
Fig.18. Calculated HMX/LiF interface wave profiles with a thickness of 0.5,1.0,2.0,and 3.0 mm at (a) 300 K, (b) 373 K, and (c) 423 K.

Fig.18 shows not only attenuation of stress relaxation but also the elastic precursor decay.To investigate the precursor decay with thickness at different initial temperatures,Fig.20 plots the dynamic yield limits σHELas a function of thickness at different initial temperatures. The calculated trend and amplitudes of dynamic yield limits at 300 K are consistent with the experimental data of Dick et al.[9].At different initial temperatures,a fast precursor decay is observed with thicknesses of below 1 mm, followed by a much lower decay rate.

The elastic precursor decays with different thicknesses is intimately related to wave propagation. Fig. 21 presents particle velocity and mobile dislocation density profiles in a 3 mm HMX single crystal at 300 K at different times.At the first stages of deformation with propagation distance of below 1 mm, the sharp precursor is accompanied by a rapid increase in the mobile dislocation density.As the shock wave propagates in the HMX,the stress drops due to plastic relaxation,which leads to a relative slow increase in mobile dislocation densities as shown in Fig. 21 (b). Therefore, the plastic deformation is accommodated by dislocation generation at shorter propagation distance, which leads to the fast precursor decay.

Fig.19. (a) Relationship between resolved shear stress and plastic shear strain rate and (b) Interface mobile dislocation density histories with different thicknesses at 300 K.

Fig. 20. The dynamic yield limits σHEL as a function of thickness at different initial temperatures.

Fig. 21. (a) Particle velocity and (b) mobile dislocation density profiles in a 3 mm HMX single crystal at 300 K at different times.

When the propagation distance exceeds 1 mm, plastic deformation is mainly accommodated by dislocation motion,which can decrease the necessity of dislocation generation. Furthermore, the plastic shear strain rate corresponding to the precursor decreases from 6 × 106s-1at anvil/HMX interface to 5 × 104s-1at about 2.5 mm. Consequently, the precursor decays slowly due to the lower plastic shear strain rate governed by dislocation glide. According to the observed precursor decay in a 3 mm HMX single crystal at 300 K,a rapid decay rate with thicknesses of below 1 mm at different initial temperatures is attributed to the fast dislocation generation. While the subsequent slower decay rate is due to the attenuation of plastic wave, which leads to the reduced plastic shear strain rate.

5. Conclusions

The plate impact experiments at temperatures of 373 K and 423 K were conducted to investigate the shock response of HMX single crystals at elevated temperatures(below the phase transition point). To further investigate the related mesoscale deformation mechanisms, a thermomechanical dislocation model for HMX single crystals subjected to high strain rates and high temperatures was developed. The model could well reproduce the measured thermal hardening behavior of HMX single crystals in plate impact experiments. From comparison of the related dislocation physical quantities,the mechanism of thermal hardening is well explained.Additionally, the calibrated model was utilized to predict shock response of HMX single crystals with different thicknesses at different initial temperatures. The stress relaxation and elastic precursor decrease with thickness were observed.

Wave profiles of HMX single crystals at different initial temperatures exhibit a distinct elastic-plastic double wave structure including the elastic precursor, stress relaxation, and the arrival of subsequent plastic wave. As temperature increases to 423 K, the HEL increases abnormally, showing thermal hardening behavior.

Comparing the mobile dislocation density histories with the average dislocation velocity histories,it is found that the increase of HEL with temperature is dominated by dislocation mobility.Furthermore, the model suggests that the reduced dislocation motion is attributed to the increased phonon drag coefficient,which is induced by phonon scattering and radiative damping.The effects of phonon scattering and radiative damping on the thermal hardening behavior were quantized. The contribution of radiative damping to thermal hardening behavior is less than that of phonon scattering. Considering that the pressure volume work and dislocation-based plasticity work contribute to the temperature rise, the temperature rises corresponding to HELs increase with temperature as expected.

Both the stress relaxation and elastic precursor decay with thickness.The rapid stress relaxation is accompanied with the fast dislocation growth, indicating that it is dominated by dislocation generation. For the precursor decay with thickness, when the thickness is below 1 mm, the fast dislocation generation is observed, resulting in a rapid decay rate at different initial temperatures. While the thickness exceeds 1 mm, the plastic shear strain rate corresponding to the precursor decreases, which indicates that the slower decay rate is ascribed to the viscous attenuation of plastic wave.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No.12172051 & No.11802024), and Beijing Institute of Technology Research Fund Program for Young Scholars(WXJ2019).