An improved SLAM based on RK-VIF: Vision and inertial information fusion via Runge-Kutta method

Ji-shn Cui , Fng-rui Zhng , Dong-zhu Feng ,*, Cong Li , Fei Li , Qi-hen Tin

a School of Aerospace Science and Technology, Xidian University, Xi'an, 710126, China

b China Academy of Space Technology, Xian Branch, Xi'an, 710100, China

c China Academy of Launch Vehicle Technology, Beijing,100076, China

d Aerospace Information Research Institute, Chinese Academy of Sciences, Jinan, 250100, China

Keywords:SLAM Visual-inertial positioning Sensor fusion Unmanned system Runge-Kutta

ABSTRACT Simultaneous Localization and Mapping (SLAM) is the foundation of autonomous navigation for unmanned systems.The existing SLAM solutions are mainly divided into the visual SLAM(vSLAM)equipped with camera and the lidar SLAM equipped with lidar. However, pure visual SLAM have shortcomings such as low positioning accuracy,the paper proposes a visual-inertial information fusion SLAM based on Runge-Kutta improved pre-integration. First, the Inertial Measurement Unit(IMU) information between two adjacent keyframes is pre-integrated at the front-end to provide IMU constraints for visual-inertial information fusion. In particular, to improve the accuracy in pre-integration, the paper uses the Runge-Kutta algorithm instead of Euler integral to calculate the pre-integration value at the next moment.Then,the IMU pre-integration value is used as the initial value of the system state at the current frame time.We combine the visual reprojection error and imu pre-integration error to optimize the state variables such as speed and pose,and restore map points'three-dimensional coordinates.Finally,we set a sliding window to optimize map points' coordinates and state variables. The experimental part is divided into dataset experiment and complex indoor-environment experiment.The results show that compared with pure visual SLAM and the existing visual-inertial fusion SLAM, our method has higher positioning accuracy.

1. Introduction

Recently, autonomous navigation based on unmanned systems is gradually being used in various fields.SLAM is the foundation and core of autonomous navigation [1]. The SLAM method refers to unmanned systems establishing the environmental map and estimating its trajectory during the movement under the unknown environment [2]. Vision sensors rely on the image sequence captured to estimate the pose and create an environmental map.Still, when the movement is too fast or the environment features are missing, its accuracy and robustness will decrease sharply and sometimes even lead to positioning failure [3,4].

With the continuous advancement of hardware technology,low-cost IMU has become ubiquitous[5,6].IMU and vision sensors have strong complementarity in performance. Therefore, the Visual-Inertial Navigation System (VINS) has gradually become a hot topic in the current SLAM field [7].

The main goal of VINS is to better couple IMU measurement and image information.According to the coupling scheme,VINS can be divided into loosely coupled systems and tightly coupled systems.The loose coupling uses the knowledge of the camera and IMU to estimate the motion of the system and then combines the estimation results.In contrast,the tight coupling method establishes a unified objective function for the camera and IMU state information and then performs the system motion estimation.

According to the data processing method, VINS can be divided into the filtering-based method and optimization-based method.Filtering-based methods generally choose the EKF framework,which is divided into two stages: prediction and update. The prediction stage uses IMU information to predict the system pose;and then in the update stage, the system state is corrected and optimized according to the image information. The optimizationbased method considers the data of a period in the past and then iteratively optimizes the system state[8,9].For the reason that the filtering-based method only considers data at the current moment and only uses image information when updating the state, its accuracy is limited; therefore, the current mainstream VINS choose the optimization-based method.

Limited by processor performance in the early days, VINS research was mainly based on filtering. Mourikis et al. proposed a filter-based tight-coupling scheme-MSCKF, which is the first relatively mature scheme in the field of VINS[10].MSCKF uses a feature point to constrain multiple camera motion states at different moments and uses multi-state constrained extended Kalman filtering as the back-end. At the same time, it adopts a sliding window strategy to ensure the real-time performance of the system. However, since only monocular camera is used in the MSCKF, the accuracy of visual-inertial odometry (VIO) is quite insufficient compared to stereo camera. The problem of autonomous underwater vehicles' SLAM has been solved in Ref. [11]. Aiming at the problem of nonlinear models and non-Gaussian noise in AUV motion, the author proposes an improved variance reduction Fast-SLAM with simulated annealing to solve the problems of particle degradation, particle depletion and particle loss in traditional FastSLAM.Bloesch et al.proposed a robust visual-inertial odometry(ROVIO), which also uses a tight coupling solution based on filtering.The ROVIO front-end adopts the direct method to track the camera movement by minimizing the photometric error of the image block, and the extended Kalman filter at the back-end can follow the image block features and three-dimensional landmark points at the same time [12]. However, ROVIO doesn't have a loop detection module, it is only an odometry, and there is a sizeable cumulative error in the long term.

In recent years,with the continuous improvement of processor performance,the optimized VINS has gradually become the current hot point. Leutenegger et al. proposed the keyframe-based visualinertial SLAM using nonlinear optimization (OKVIS) [13]. Its frontend uses multi-scale Harris corner detection features and BRISK descriptors.OKVIS pre-integrates the IMU information between the keyframes in the back-end and then estimates the system moves through vision and IMU information.However,the scheme doesn't have loop detection and pose graph optimization,which inevitably causes error accumulation. Raul et al. proposed VIORB-SLAM[14,15] based on ORB-SLAM by fusing IMU information, which also adopts a tight coupling scheme based on optimization. Its front-end uses ORB features, pre-integrates IMU data, and then uses the g2o library to fuse the two information to estimate the system motion. The accuracy of VIORB-SLAM is much better than monocular ORB-SLAM.Still,the code is not open-source,and it only supports monocular cameras,which require complex initialization before using [16].

Shen Shaojiao et al. proposed the robust and versatile monocular visual-inertial state estimator (VINS-Mono),which still uses a tight coupling scheme based on optimization. However, VINSMono only supports monocular cameras. Its front-end uses the KLT optical flow method to track Harris corners.It also uses the preintegration idea to process IMU data and then fuses the two sensor information through iterative optimization [17].In addition,VINSMono can be initialized in an unknown environment and has a loop detection module [18,19], but the accuracy needs to be further improved. Later, the Shen Shaojiao team released VINS-FuSion based on VINS-Mono. VINS-FuSion retains an optimized tightly coupled fusion scheme and supports multiple types of sensor combinations (pure binocular, binocular + IMU, and binocular + IMU + GPS). Compared with VINS-Mono, it can be initialized statically,and the scale information doesn't entirely rely on the IMU, which is more robust. However, because of stereo vision's mismatch problem,its accuracy is not even as good as VINSMono in some situations.

Although existing visual-inertial information fusion SLAM systems are emerging one after another, the visual and IMU information still cannot be effectively integrated.Solving the frequency inconsistency between the camera and IMU and fully integrating the visual and IMU information is still an urgent problem for VINS.A suitable SLAM should be able to fully integrate visual and IMU information, significantly to improve the positioning accuracy and robustness of the system in extreme situations such as lack of environmental information and rapid carrier movement.Therefore,this paper proposes a visual-inertial information fusion SLAM based on Runge-Kutta improved pre-integration, aiming to improve the accuracy and robustness of the system.

The sections of our paper are arranged as follows: the second section introduces the visual-inertial information fusion framework. The third section introduces the SLAM method of visualinertial information fusion based on Runge-Kutta 4 improved pre-integration. The fourth section introduces the experimental part of our paper, including dataset experiments and experiments in complex indoor environment. Finally, the fifth section summarizes the paper and gives conclusions.

2. RK-VIF: system overview

Pure visual SLAM can estimate the pose of unmanned system and create featured map in unknown environment. Visual information has no data drift,and the positioning accuracy is higher in rich image features areas;however,if the image features are less or the movement is too fast,it is difficult for pure visual SLAM to work robustly, or even lead to positioning fails; IMU doesn't depend on environmental characteristics, and the measurement frequency is higher than camera. IMU relative displacement data has high accuracy in a short time,which can make up for the shortcomings of the visual blurring due to fast motion;however,excessive IMU use will cause errors to accumulate with time, and then produce extremely serious drift error. Aiming at the shortcomings of IMU,visual SLAM can constrain the divergence generated by IMU for a long time. Thus, IMU and camera are highly complementary in performance.Therefore,the paper fuses IMU information based on the visual SLAM,studies visual-inertial information fusion SLAM to improve the system's positioning accuracy. As shown in Fig.1, the visual-inertial information fusion SLAM framework of this paper mainly includes four modules: measurement data processing,system initialization, joint state estimation and sliding window local optimization, and loop detection.

3. Measurement process

3.1. Feature extraction and matching

In the visual SLAM based on the feature point method, feature point extraction and matching are first required.The purpose is to determine the projection of the same spatial point in different images according to the extracted features. Feature extraction generally includes two parts: feature point detection and description. First, the critical information in the image is detected, and then it is represented by feature descriptors. Then, by comparing the distances of feature descriptors, the correspondence between feature points in different images can be matched. Usually, there are many mismatched points in the matched image, which will affect the accuracy of the subsequent pose estimation.Therefore,it is necessary to use the mismatch elimination algorithm to eliminate the abnormal points.

The current visual SLAM method usually uses the Random Sampling Consensus(RANSAC)algorithm to eliminate mismatched points. Although the RANSAC algorithm can effectively eliminate mismatched points, the randomness of the algorithm itself causes the number of iterations to be unstable, which in turn causes problems such as low elimination efficiency. Therefore, this paper introduces the Progressive Sampling Consensus (PROSAC) algorithm[20]to eliminate mismatched points.The PROSAC algorithm can solve the problems of unstable iterations and poor robustness of the RANSAC algorithm, effectively improve the algorithm's efficiency, and provide a guarantee for the real-time performance of SLAM.

The PROSAC is based on the assumption that “the points with good quality are more likely to be interior points” [21]. Therefore,when selecting sample points,the points with good quality will be chosen first. Specifically, the PROSAC first uses certain criteria to evaluate the quality of all sample points,and then sorts them by the evaluation results, the algorithm only high-quality sample points are selected to estimate the matching model every time. Through the sorting strategy, the randomness of algorithm sampling is avoided,the probability of obtaining the correct model is improved,and the number of algorithm iterations is reduced.

The steps of the PROSAC algorithm are shown in Fig. 2:

3.2. IMU pre-integration based on Runge-Kutta

In the VINS, the camera is an external sensor that collects environmental information and determines the system's pose during movement; IMU is an internal sensor that provides the system's movement information and restores the gravity direction of the visual SLAM.The IMU measurement value will be affected by Gaussian noise and zero bias. In order to simplify the model, it's assumed that each axis of the accelerometer and gyroscope are measured independently, and the influence of the earth's rotation is not considered. The measurement process can be modeled as follows [22,23]:

According to the rigid body kinematics model,the motion state of the body system in the world coordinate system satisfies the following differential formula:

In formula, aB|Wrepresents the acceleration of the body coordinate in the world coordinate,and vB|Wrepresents the speed of the body coordinate in the world coordinate.

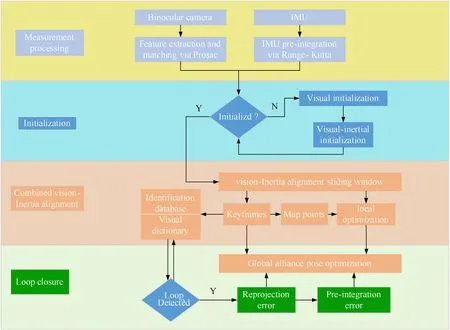
Fig.1. Visual-inertial information fusion framework.

Suppose the time difference between two IMU measurements is Δt. Assuming that the acceleration aB|Wand the angular velocity vB|Wremain constant within [t,t +Δt], substituting the IMU measurement model of formula (1) into formula (2):

In formula, ηgd（t) and ηad（t) are the discrete values of random noise ηg（t) and ηa（t) respectively.

Traditional pre-integration uses Euler integral to discretize the IMU motion formula and then derives the IMU pre-integration formula. Our paper uses the Runge-Kutta method to discretize the IMU motion formula to improve the pre-integration accuracy.The basic idea of the Runge-Kutta method is to estimate the derivatives of multiple points in the integration interval, take the weighted average of these derivatives to obtain the average derivative,and then use the average derivative to estimate the result at the end of the integration interval. If Runge-Kutta algorithm's order is higher,it will lead to smaller truncation error of the system,and improve algorithm's accuracy. In practical applications, the fourth-order Runge-Kutta algorithm can already meet most of the accuracy requirements. Considering the computer processor's performance, the paper use the fourth-order Runge-Kutta algorithm.

Given the following differential formula:

Euler integral uses the derivative f（tn,yn) at point tnas the derivative of the interval[tn,tn+1],and updates it with the state ynat point tn. There are:

In formula,Δt =tn+1-tn.Euler integral only uses the derivative information at point tn, so it has a higher estimation error.

The Runge-Kutta algorithm is an improvement of Euler integral.It selects four points in the interval [tn,tn+1], calculates the derivative k1～k4of four points by iterative method,and then takes the weighted average of these derivatives to calculate the next state yn+1. The formula of the fourth-order Runge-Kutta algorithm is as follows:

In formula,

In formula, k1represents the derivative at the beginning of interval （tn,yn);is the midpoint of the interval estimated by Euler integral method using k1as the average derivative, and k2represents its derivative;is the midpoint of the interval estimated by Euler integral method using k2as the average derivative, and k3represents its derivative;（tn+Δt,yn+k3•Δt) is the end point coordinates of the interval estimated by Euler integral method using k3as the average derivative, and k4represents its derivative. From formula (7), it can be seen that the algorithm integrates the derivative information of the four points, and the derivative at the two midpoints has a higher weight.

Our paper use Runge-Kutta method discretize the IMU motion formula in formula (3):

ωWB-RK|Band aB-RKare the weighted average values of the angular velocity and acceleration of the system obtained by Runge-Kutta algorithm within [k,k + 1]. Compared with only using the angular velocity ωkWB|Band acceleration akBat moment k to recursively calculate the system state at moment k+ 1, ωWB-RK|Band aB-RKhave higher accuracy.

As shown in Fig. 3, the IMU frequency is much higher than the camera frequency, and there are much IMU data between two adjacent keyframes [24,25]. Therefore, the IMU data cannot be directly fused with the camera data.The IMU data between the two frames must be integrated to align the frequencies of the two sensors.

Fig. 2. The process of PROSAC algorithm.

Fig. 3. Sensor frequency.

Assuming that the IMU information and the camera image are synchronized in time, only the frequency is different. We accumulate the IMU information from the moment i to the moment j.The state variables such as the rotation, speed, and translation of the system at moment i can be directly updated to the moment j.Combining formula (8), the numerical integration of IMU information between adjancent keyframes i and j satisfies the following formula:

Formula (9) describes the state estimation obtained by IMU information from moment i to moment j.But if RiWBchanges during the optimization process, all other rotation RkWB（k=i, … ,j-1)will change, and all integrals need to be recalculated. In order to avoid the problem of repeated integration,we use the form of preintegration to define a set of variables that are not related to the initial pose and velocity:is the pre-integrated measurement of rotation between adjacent keyframes,and RiBWRi+1WBis the rotation matrix estimated by vision.Formula (11) is a least-squares problem. The Gauss-Newton method can find the zero bias of the gyroscope. After calculating the gyroscope zero bias, in order to eliminate the influence of the gyroscope zero bias on the pre-integration, it is necessary to recalculate the pre-integration on the IMU data.

In formula, ΔRi,k= RiBW∙RkWB, Δvi,k= RiBW∙（vkB|W- viB|W-gW∙Δti,k). The left side of formula (10) is the relative motion increment between adjancent keyframes i and j,and the right side is the IMU pre-integration measurement model. The definition makes the right side of the formula independent of the state and gravity at moment i.Repeated integration in the calculation process is solved, and calculation is significantly reduced.

3.3. System initialization

VINS initialization is a loosely coupled process of visual estimation and IMU estimation [26]. Firstly, perform visual initialization, estimate the initial pose of the system from the matching image. Then initialize the zero bias of the gyroscope and accelerometer by the estimation results, and calculate the speed of the IMU.

Assuming that the gyroscope bias remains constant between two consecutive keyframes, minimize the difference between the gyroscope pre-integrated measurement and the visual estimated relative rotation, and calculate the gyroscope bias:

N is the number of keyframes required for initialization,ΔRi,i+1

In order to get the zero bias of the accelerometer, firstly, we estimate the gravitational acceleration through the posture of visual SLAM. Then we calculate the zero bias [27]. The conversion relationship between the body coordinate system and the camera coordinate system in the world coordinate system satisfies:

pB|Wand pC|Wrespectively represent the position of IMU and camera in the world coordinate system,RWCdescribes the rotation matrix of the camera coordinate system relative to the world coordinate system.Meanwhile,pB|Crepresents the position of IMU in the camera coordinate.

Introducing the constraint of gravitational acceleration G≈9.8,suppose a body coordinate system I, which shares the origin with the world coordinate system. The rotation matrix between the body coordinate system and the world coordinate system is RWI.The direction of gravitational acceleration in the body coordinate system I is= [0,0,1]T, and the direction of gravitational acceleration in the world coordinate system is=g*W/‖g*W‖,so the angle between these two direction vectors can be used to calculate RWI.

At this time,the acceleration of gravity gWcan be expressed as:

RWIwill change after the accelerometer zero bias is introduced.We use disturbance δθ to describe the change and perform the firstorder approximation:

Combining formula (9) and formula (12), considering the change of the accelerometer zero bias to Δpij, and considering the constraints between three consecutive keyframes, eliminating the velocity term,we can get the following formula:

where,

3.4. Joint estimation and local optimization

The initial velocity, gravitational acceleration, and zero bias of the gyroscope and accelerometer are solved through the IMU initialization.Then we use image and IMU information to estimate and optimize the system's pose. First, the joint estimation calculates the system's pose at the current keyframe by minimizing the visual reprojection error and the IMU pre-integration error. Then,the system's pose and the map points'location are optimized in the sliding window.

We use Singular Value Decomposition (SVD) to solve formula(15), the zero bias baof the accelerometer and the optimized gravity acceleration can be obtained.

According to the calculated zero bias of the gyroscope and accelerometer, combined with formula (9), the system speed at each keyframe moment can be further obtained.The system speed at the last keyframe is:

The system speed at other keyframe moments is:

3.4.1. State and error

The state variables of the VINS includes rotation matrix, translation matrix and speed.IMU bias is a random walk process,which also needs to be estimated.Define the ith frame's state as Φi={Ri,pi,vi,bgi,bai}.In the subsequent local optimization process,the map point's location in the sliding window needs to be jointly optimized as the state.

As shown in Fig. 4, the VINS includes three constraints:

Fig. 4. VINS state and constraints.

●The constraint of image feature points'position between the keyframe and the map points;

●The constraint of IMU pre-integration measurement between adjacent keyframes;

●The constraint on the random walk model of the zero bias between adjacent keyframes.

According to the above constraints, we define the visual reprojection error and IMU measurement error. The two types of errors are introduced below.

Visual error is defined by the reprojection error of the map point.Assuming that m map points are observed at the time of the ith frame,the visual error at that time is

In formula,ρ is the kernel function,is the covariance matrix of the reprojection error. Meanwhile, xkuv=（ukL,vkL,ukR) is the projection coordinate of the kth landmark point obtained by the stereo camera,XkC=[X,Y,Z]is the landmark in camera coordinate,and π is the projection formula:

fx,fy,cu,and cvare the internal parameters,and bl is the baseline.The IMU error comprehensively considers the two constraints,including the IMU pre-integration measurement and the zero bias random walk process. The IMU error between frame i and j is defined as:

In formula,ΣIMUis the pre-integrated measurement covariance matrix;Σbis the zero-biased random walk covariance matrix;eIMUis the IMU pre-integrated measurement residual,and ebis the IMU zero-biased random walk residual:

In formula,

3.4.2. Joint state estimation

The joint state estimation measures the system pose in realtime. First, IMU provides the system with a relatively credible initial estimate,reprojects the map points observed in the previous keyframe into the current keyframe. Then, the system calculates the visual reprojection error for all projection points and their matching points in two adjacent keyframes. Finally, it minimizes the sum of visual reprojection error and IMU pre-integration error.Formula (19) defines the visual error Eproj（j), and formula (21) defines the IMU error EIMU（i,j). Therefore, the objective function is defined as:

The above problem is a least-squares problem. Therefore, the optimal state Φ*can be solved by minimizing the sum of the visual reprojection error and the IMU error.

3.4.3. Local sliding window optimization

The state information of the latest keyframe is estimated through the joint state estimation module, and the observed landmarks are added to the local map to become map points.Next,we optimize the system pose and map point locations in the local map.

In the VINS, since the IMU provides constraints between two adjacent keyframes,the keyframes contained in the local map must be continuous before they can be used for optimization.At the same time, the computational complexity after fusion will increase rapidly because of the high frequency of IMU. To balance accuracy and calculation efficiency, we choose the sliding window strategy to optimize the local map. As shown in Fig. 5, the continuous keyframes in the most recent period of time constitute a sliding window. During the optimization process, only the keyframes in the sliding window and the map points observed by these keyframes are optimized.In our paper,the sliding window's length in the local map is set to 10 to ensure reliability.The method ensures that the IMU pre-integration can provide effective constraints during local optimization (see Fig. 6).

Fig. 5. Sliding window optimization range.

Fig. 6. Loop detection process.

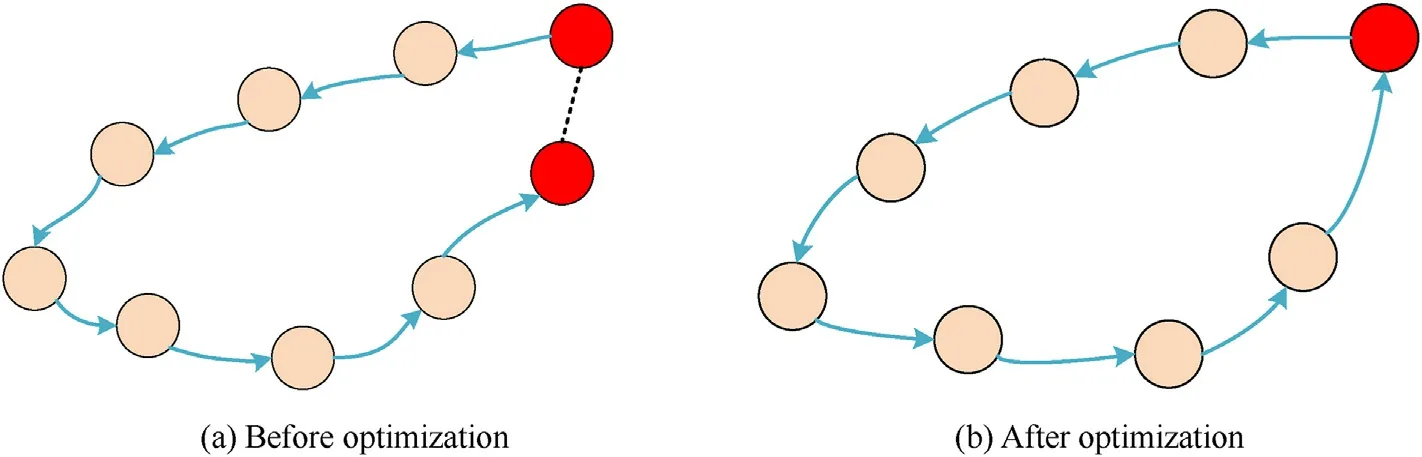
Fig. 7. Globally optimized pose.

The state at this moment is defined as:

In formula, k represents the keyframe's subscript in the sliding window, TkWBrepresents the system pose in the world coordinate system at the kth keyframe. Meanwhile, XiWrepresents the ith landmark's coordinate in the world coordinate system.

Combine the reprojection error and the IMU pre-integration error of all keyframes in the sliding window to construct the objective function:

Formula(26)is still a least-squares problem,and it is still solved by the Gauss-Newton method in g2o.

The local sliding window optimization comprehensively considers the status information of consecutive N keyframes, and update the system pose in the sliding window at each iteration.After completing local optimization, the loop detection module will perform loop detection and global pose graph optimization on the latest keyframes to eliminate accumulated errors and optimize the system pose.

3.5. Back-end optimization

Unmanned systems explore in an unknown environment, and there is always an error estimating their pose.Due to expanding the exploration area, the previous errors will gradually accumulate to the next moment. Therefore, correcting the pose in time is particularly important for the long-term robust running of the unmanned system.In order to solve this problem,the feasible idea is to detect the image information in the scene and determine whether the current position is a place that has been reached before. If the information is found to be similar, a loop is formed at the repeated position. Then, re-optimize the system's pose in the loop to eliminate accumulated errors and obtain a globally consistent pose graph.

The loop detection based on the scene's appearance is essentially an image similarity detection problem. However, suppose all historical frames in the map are matched with the current frame.In that case, calculation is too large, which seriously affects the realtime detection. In this paper, we use the Bag of Words (BoW)model to accomplish loop detection.

The words in the BoW model are the average expression of similar features those have a specific type, and the dictionary is a collection of all words.We use the ORB features extracted from the front-end. For the frame, compare the ORB feature and dictionary elements to convert the frame into a bag-of-words vector. In loop detection, by comparing the bag-of-words vectors of the two frames,it can be judged whether the two frames constitute a loop to speed up the detection. The detection process includes the following three parts: (1) building a dictionary; (2) using bag-ofwords vectors to describe frames; (3) comparing the bag-ofwords vectors to determine the similarity of two frames.

After the system successfully detects the loop, it can establish the constraint relationship between the two frames through feature matching.Firstly,we need to fuse the map points matched by the loop and eliminate redundant map points.Then calculate the relative pose between the two keyframes according to Perspective-N-Point (PnP) algorithm, and correct the current keyframe's pose.In addition,other keyframes in the loop also have different degrees of accumulated error and need to be globally optimized.

Considering that the number of map points is much larger than the number of keyframe poses, we only optimize each keyframe pose in the global optimization process to reduce calculation.After the pose optimization is completed, we use the optimized pose to adjust the map point.

In the pose graph optimization,the nodes represent the camera poses, and the edges represent the pose transformation relationships between adjacent nodes. Suppose the camera poses of two adjacent nodes in the loop are Tiand Tj, the pose transformation matrix is Ti,j, and the corresponding Lie Algebras are expressed as ξi, ξj, and ξi,jrespectively. According to the relationship of pose transformation:

Due to the pose estimation error,the above formula will not be accurate.The pose estimation of unmanned systems is to iteratively solve an optimal transformation matrix T∊SE（3),so as to minimize the system error.In order to simplify the iterative solution process,Lie algebra is introduced,so we can transform the matrix derivation to multiplying the matrix by the vector which corresponding to the anti-symmetric matrix.We stipulate that the symbol‘∨’represents the conversion of an anti-symmetric matrix to corresponding vector, and the symbol ‘∧’ represents the conversion of a vector to corresponding anti-symmetric matrix. Thus we can construct the error term by moving Ti,jto the right side of formula (27):

Formula (28) describes the error term between two adjacent pose nodes.Considering the error term formed by all pose nodes in pose graph to build a least-squares problem:

where,ξ is the set of all nodes in the pose graph,ε represents the set of all edges in the pose graph. Σ i,jis the information matrix, representing the weight of error term ei,j.

Finally,we use g2o to solve the above least-squares problem,the poses of all keyframes in the loop are corrected,and the position of all map points is re-adjusted. Fig. 7 shows the pose graph. Due to the accumulation of errors, the unmanned system motion trajectory does not form a closed loop when the previous position is accessed.Pose optimization can align the system poses at the same place and correct the system global motion trajectory.

4. Experiment

We evaluate the proposed visual-inertial information fusion algorithm through two parts: dataset experiment and real environment experiment. We compare the proposed visual-inertial information fusion algorithm with other latest algorithms on a public dataset in the first experiment. The comparison of experimental data proves the positioning accuracy and robustness of our algorithm in detail. Then, we test the algorithm in an indoor environment to evaluate its performance in real scenarios.

4.1. Dataset experiment

The experimental platform configuration for our experiment is shown in Table 1.The open-source dataset EuRoC provided by ETH Zurich is used to verify the SLAM algorithm. The EuRoC dataset is collected on a micro-drone containing 20 Hz binocular images provided by MT9V034 camera, IMU information of synchronous 200 Hz provided by ADIS16448 sensor, and actual trajectory provided by a motion capture system. Therefore, it is very suitable to verify the visual-inertial information fusion SLAM algorithm.

Table 1 Experimental platform configuration.

The dataset includes 11 data sequences collected during the flight of the micro-drone shown in Fig. 8(a) in an industrial plantand two rooms.According to the camera data sequence's exposure change,feature number,motion speed,and motion blur degree,the EuRoC dataset divides 11 data sequences into three levels: easy,medium,and difficult.Among them,the maximum speed of 7 data sequences exceeds 2 m/s,and the highest speed can reach 2.87 m/s.The average speed of three data series exceeds 0.9 m/s. Fig. 8(b)shows the images collected by the micro-drone in an industrial plant. The environment in the plant is relatively complex and can fully simulate the actual setting of unmanned systems.

In order to verify the performance of the algorithm, we have done a lot of comparative experiments.To simplify the notation,we use RK-VIF(the SLAM method for visual-inertial information fusion via Runge-Kutta) to represent our algorithm and compares it with the current state-of-the-art visual-inertial information fusion system OKVIS, ROVIO, and VINS-Mono. OKVIS is an advanced VIO algorithm developed by the Automation System Laboratory of ETH Zurich,which can be used with monocular or stereo cameras;VINSMono is a tightly coupled monocular visual-inertial system developed by the team of Mr.Shaojie Shen from HongKong University of Science and Technology;ROVIO was developed by ETH Zurich as a tightly coupled monocular visual-inertial system. This part of the simulation experiment details the results of the MH_05_difficult and V1_02_medium sequences in the EuRoC dataset.

For sequence MH_05_difficult and sequence V1_02_medium,the running trajectory graph of ROVIO,OKVIS, RK-VIF, and Ground Truth is shown in Fig. 9.

Through multiple comparison experiments, we give the Root Mean Square Error (RMSE) of various algorithms under each sequence in the EuRoC dataset to evaluate the performance of multiple algorithms.

The RMSE of 10 sequences in the EuRoC dataset is shown in Table 2. Compared with other algorithms, RK-VIF has the smallest RMSE in most data sequences, indicating that RK-VIF has the highest positioning accuracy and the best performance. However,the OKVIS has weak advantage in the sequence V2_01_easy. After comparative analysis,we think the RK-VIF has a certain positioning error when handling the sequence V2_01_easy, Unmanned aerial vehicle (UAV) moving too fast and blurred motion are the main reasons leading to the increase in RMSE. However, on the test platform of our paper, the OKVIS cannot run in real-time. Fig. 10 shows the running time of various algorithms in EuRoC dataset.The blue column represents Ground Truth, which is the actual shooting time of every sequence. It can be seen that the running speed of our algorithm is better than ROVIO. However, compared with the VINS-Mono, the running time is longer under certain sequences. It is because the algorithm costs long time in matching feature points and using Runge-Kutta for pre-integration; OKVIS has the longest running time.Analysis of the possible reason is that it takes a long time in the process of image feature extraction and global pose optimization. In summary, our experiments verify algorithm's performance in our paper in terms of running accuracy and running speed. Our algorithm satisfies the long-term and stable operation of the SLAM system.

Table 2 The RMSE in EuRoC Dataset (unit:m).

Fig. 8. EuRoC dataset.

Fig. 9. Dataset experiment.

4.2. Real environment experiment

In the actual indoor experiment part, the experimental environment is shown in Fig.11(a). Our article uses indoor GPS as the Ground Truth.We compare the RK-VIF with OKVIS,VINS-Mono and ROVIO to verify the performance of various algorithms.

The experimental platform used is shown in Fig. 11(b). A TX2 development board is mounted on the Mecanum wheel mobile robot.Computing resources mainly include CPU:HMP Dual Denver 2/2 MB L2 + Quad ARM A57/2 MB L2, GPU: NVIDIA Pascal, 256 CUDA Cores, connected to a ZED binocular camera and an STM32 driver board, equipped with IMU sensor MPU-6050.

In this experiment,we tested the positioning accuracy of ROVIO,OKVIS,VINS-Mono,and RK-VIF.Connect the laptop and TX2 to the same local area network (LAN). We use laptop to control the TX2 mobile robot and run three circles in the indoor experimental environment with the same trajectory, as shown in Fig.12. Indoor GPS obtains ground truth, and the total track length is 72.72 m.Fig. 13 and Fig. 14 respectively show the translation and rotation information of the mobile robot at each moment and the corresponding error.

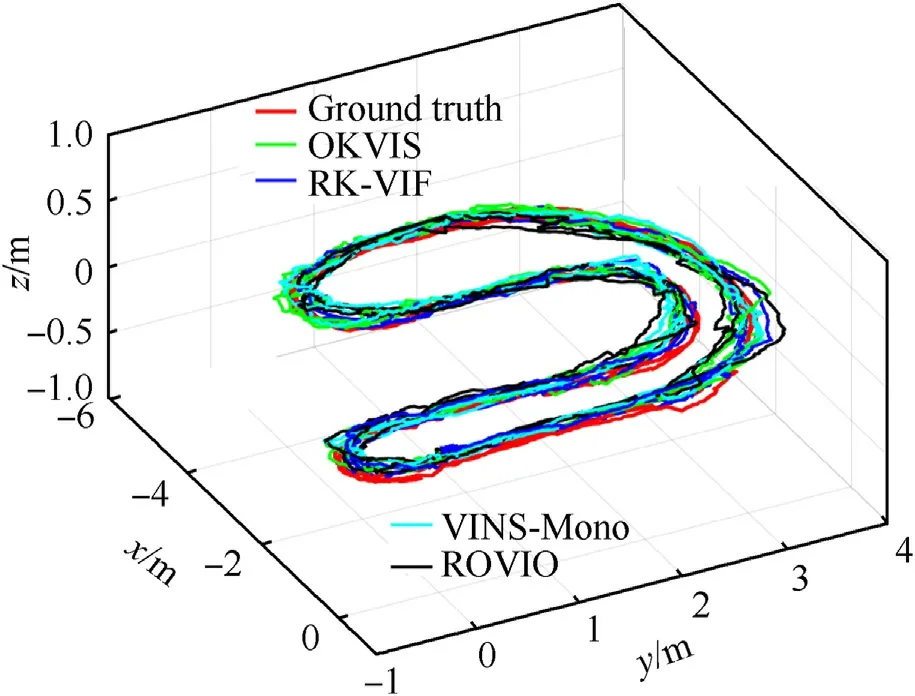
Fig.12. Running trajectory in indoor environment.

Fig.10. Running time in EuRoC Dataset (unit: s).

Fig.11. Test environment and equipment.

The RK-VIF, ROVIO, OKVIS, and VINS-Mono are compared and analyzed in the indoor environment experiment. Comparing the ground truth generated by indoor GPS in the X and Y directions,the RK-VIF algorithm has the least trajectory error and the highest positioning accuracy, which is between -.0.2m ～+ .0.2m. The second is the VINS-Mono, and the third is the OKVIS. The worst ROVIO has a trajectory error of±.0.3m;in the Z direction,due to the mobile robot is always on the same horizontal plane. The position information at each moment fluctuates around 0, which is in line with actual changes.

Considering the actual situation of the indoor experimental site flat and no slope,in the attitude error comparison,we do not count the roll angle and pitch angle;only the yaw angle is included in the category of attitude error analysis.

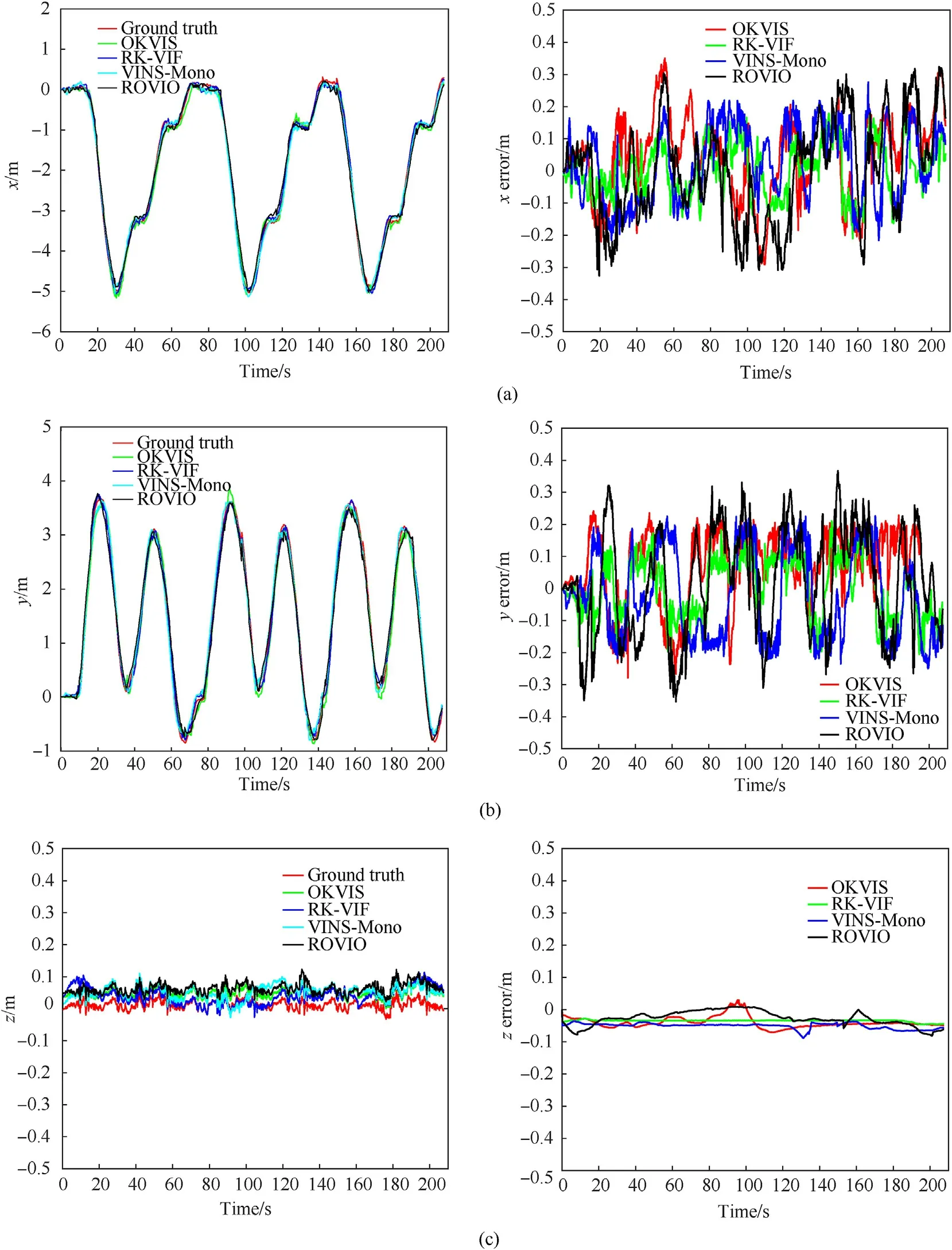
Fig.13. The position and their corresponding errors of various algorithms.

As shown in Fig. 14, comparing the four algorithms of RK-VIF,OKVIS, VINS-Mono, and ROVIO, the attitude error of the RK-VIF is significantly smaller than the other three algorithms and the error is between -4°～+4°.However,OKVIS and VINS-Mono have similar attitude errors,and ROVIO has the largest error, reaching± 6°.

Figs.13 and 14 analyze the positioning errors of the four algorithms under the same experimental conditions and scene in the form of a relationship diagram. In order to more intuitively demonstrate the advantages of our algorithm, we analogy to the dataset experiment in chapter 4.1. In Table 3, we conduct five experiments for each algorithm and give the best result of the RMSE in the indoor environment.It can be seen from the table that RK-VIF has smaller positioning errors and better robustness in actual scenes. Thus, integrating the two parts of the dataset and actual scene experiments, our algorithm considers the positioning accuracy and running time,providing a more excellent solution for the unmanned system to explore the unknown environment robustly.

Fig.14. The attitude and corresponding errors of various algorithms.

Table 3 The average RMSE in indoor environment(unit: m).

5. Conclusion

This paper proposes a visual-inertial information fusion SLAM based on the Runge-Kutta improved pre-integration,aiming at the low positioning accuracy of pure visual SLAM in fast motion and complex indoor-environment. In the process of visual-inertial information fusion, the IMU pre-integration value is used as a constraint between two adjacent frames. In order to calculate the pre-integration value, the paper uses the Runge-Kutta instead of Euler integral to discretize the IMU motion equation,so as to avoid the error caused by the first-order approximation.The experiments show that RK-VIF can effectively perform positioning estimation in environments of different difficulty levels.Furthermore,compared with other current state-of-the-art open-source algorithms, our method shows higher positioning accuracy.However,we still need extensive research further to improve the accuracy and robustness of the system.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the China Postdoctoral Science Foundation under Grant 2019M653870XB, National Natural Science Foundation of Shanxi Province under Grants No.2020GY-003 and 2021GY-036, National Natural Science Foundation of China under Grants 62001340 and Fundamental Research Funds for the Central Universities,China, XJS211306 and JC2007.