高超声速飞行器自适应减阻盘动态减阻机理
韩荣,刘伟,杨小亮
国防科技大学 空天科学学院,长沙 410073
为了改善头部驻点处气动加热效应,高超声速飞行器头部通常采用钝头体外形。在高超声速来流中,钝头体前方会形成较强烈的弓形激波,机体前后压差陡增。研究表明,激波阻力占高超声速飞行器整机阻力的80%以上[1],导致飞行器有效载荷显著降低,同时增加了控制难度[2],给飞行安全带来了极大的隐患。目前,高超声速钝体飞行器的减阻方法主要包括前缘凹腔、沿驻点线能量沉积、头部加装减阻杆以及它们的组合构型[3]等,其中减阻杆(顶端可加装圆盘等不同外形,即减阻盘)是最为简单有效的一种方法。
同时,未来飞行器对机动性和敏捷性提出了更高的要求。在机动飞行过程中,随着攻角增加,传统固定式减阻盘的效果迅速下降[4-5]。自适应减阻盘在一定程度上可以避免上述问题,即根据来流攻角自适应调整杆件方向,使减阻盘轴线始终和来流保持平行或较小偏角状态。自适应减阻盘可以较好地解决有攻角状态下减阻率下降的问题,对未来飞行器减阻系统可重复利用以及全攻角来流范围适用具有重要价值。国内外相关研究人员对此进行了一系列风洞试验及数值模拟研究。
Nicholson 等[6]在1968 年首次提出了自适应减阻杆的设计方案,借助肩部的皮托管监测飞行器迎风面与背风面的压差,然后利用压差驱动活塞、平行四边形支架等机构,进而使减阻杆对准来流,防止飞行器头部受到来流直接冲击,以保护其内部结构以及所装载的传感器等设备。Schülein 等[7-12]采用被动控制方式,参考风向标工作原理设计了一种自适应减阻盘,其自适应过程主要由飞行器两侧翼面产生的气动力矩驱动。研究发现,自适应减阻盘可以维持飞行器头部回流区的对称性,同时显著降低再附激波强度。此外,耿云飞等[13]进一步设计了一种自适应无烧蚀减阻系统,通过在杆件前端喷射冷流,可以解决有攻角状态下的减阻防热以及杆件尖端烧蚀等问题。Deng 等[14]在2017 年将自适应的概念应用到了双减阻盘结构上,对单减阻盘、双减阻盘以及是否存在安装角情况下的流场分别开展了数值仿真研究。结果显示,当安装角和攻角均为8°时,飞行器的升阻比可以达到3.634,相对原外形提高了9.1%。Huang 等[15]探讨了安装角对双减阻盘防热性能的影响,发现当杆件的安装角比来流攻角大1.5°时,钝头体-减阻盘系统的防热性能最佳。
此外,在高超声速机动飞行过程中,飞行攻角、角速度以及角加速度等运动参数发生着剧烈变化,周围流场呈现强烈的非定常效应。现有减阻方法研究主要集中在对高超声速飞行器的静态减阻性能及机理分析上,自适应减阻盘在动态过程中的现实效果以及流场特征必然和定常结果存在差异。高超声速钝头体强迫俯仰振荡问题有较多的试验和工程计算结果[16-19],而关于加装自适应减阻盘后飞行器动态特性的研究则相对较少。
针对加装自适应减阻盘的高超声速飞行器开展动态研究是飞行器减阻设计的关键环节之一,具有重要的科学价值和工程意义。因此,本文通过非定常数值模拟方法,研究自适应减阻盘在高超声速飞行器机动过程中的减阻效果和减阻机理,对比分析自适应减阻盘和传统固定式减阻盘的差异,探讨高超声速飞行器气动力特性以及流场特性随减阻盘参数的变化规律,为自适应减阻盘的设计和选型提供参考。
1 物理模型和数值方法
1.1 物理模型
以Menezes 等[20]试验中 的钝头 体外形 作为基准模型展开研究,几何模型如图1 所示。其中,钝头体顶角为120°,底部直径D=100 mm。数值计算中,参考长度取钝体底部直径D,参考面积即底部面积πD2/4。
自由来流参数与试验条件一致,其中来流马赫数为5.75,来流静温为140 K,壁面设置为等温壁,温度为300 K,其余来流条件见表1。数值模拟基于此来流条件开展。

表1 试验来流条件Table 1 Experimental conditions of incoming flow
1.2 非定常流动/运动耦合计算方法
1.2.1 非定常流体力学控制方程
飞行器机动过程涉及到网格边界运动,为精确描述动边界流动问题,基于任意拉格朗日欧拉(Arbitrary Lagrangian-Eulerian,ALE)方法建立坐标系。在ALE 坐标系中,积分形式的三维可压缩非定常Navier-Stokes(N-S)方程表示为
式中:各量均为有量纲量;Q表示守恒变量,具体表达式为
采用来流密度ρ∞、来流速度U∞、来流动力黏度μ∞以及物体的特征长度L0作为参考量,将变量和方程进行无量纲化,转换得到无量纲形式的控制方程
同时,采用AUSM 混合格式进行空间离散,时间离散使用双时间步隐式LU-SGS 方法,详情可参照文献[21]。
1.2.2 运动学方程
采用强迫俯仰振荡运动模型对高超声速飞行器开展动态气动特性研究,俯仰振荡运动可以模拟飞行中的拉升、俯冲等常用机动方式,是典型的动态非定常问题。在振荡过程中飞行器攻角按照如下规律变化:
式中:α0为初始攻角;αm表示振荡幅值;t为无量纲时间;k是减缩频率。具体定义如下:
本文主要研究高超声速飞行器在大攻角机动中的动态减阻问题,因此初始攻角取0°,振荡幅值αm=20°,振荡周期为125 s。
1.2.3 流动/运动耦合算法
高超声速飞行器机动问题需要涉及流体流动、飞行器运动及变形等多个学科领域,其中流体流动主要是求解N-S 方程,飞行器运动则通过求解运动学方程实现。本文通过图2 所示的流动/运动耦合求解方案推进求解。

图2 流动/运动耦合求解方案Fig. 2 Hydrodynamics/kinematics coupling method
在计算开始之后,首先需要对计算网格初始化,求解N-S 方程得到初始状态下的流场信息。然后通过计算运动学方程,得到飞行器在下一时刻位置和角度等参数信息;进而执行网格运动或变形,更新计算网格。接下来便采用更新后的网格进行新一轮的流场模拟。计算完成后,对流场进行后处理,输出飞行器气动力、气动力矩以及流场相关计算结果,完成计算。
为保证数值模拟精度和计算的稳定性,采用一阶隐式欧拉格式的紧耦合方法[22],通过隐式方式在每一时间步下构造多个子迭代,并在每一子迭代步骤中进行数据交换。
1.2.4 动态混合网格生成技术
高超声速飞行器动态机动问题涉及物理边界运动,其中需要处理的关键问题是动态网格的生成,本文使用的动态网格技术主要为基于径向基函数(Radius Basis Function,RBF)的网格变形技术。
基于径向基函数的网格变形方法主要分为求解和更新两个模块,其中求解模块主要涉及插值系数的确定。
在RBF 插值过程中,“中心点”表示d维欧氏空间给 定的 一组位置不同点X={xc1,xc2,…,xcn}⊆ RD,各“中心点”上对应的一系列标量值为gc1,gc2,…,gcn。RBF 插值指的是当基函数φ(x)给定时,寻找合适的连续函数:
使得条件
得到满足的过程。
显然,插值函数f(x)需要通过所有的“中心点”,因此RBF 插值的关键就是要确定插值系数γi。具体到动网格问题,插值“中心点”表示物体运动边界上的点,而相应的标量值指的是物体在3 个方向上的位移。插值系数通过式(9)确定:
式中:向量γ=[γ1γ2…γn]T;g={g(xci)}ni=1;插值矩阵M为n阶方阵,其元素为
其中:||x-xci||表示欧氏距离,在三维空间中,可以直接由r'替代:
上述插值系数的求解过程即RBF 方法的求解模块,在求解得到位移插值系数之后,将计算域内各个网格点的坐标直接代入RBF 插值函数,便可求出内场每个网格点的位移,从而完成整个计算域内的网格移动,如式(12)所示。此过程即RBF 方法的更新模块。
2 数值方法验证及网格无关性分析
2.1 数值计算方法验证
作为高超声速导弹的标准模型,HBS(Hyper Ballistic Shape)动态特性既有试验结果,也有半经验理论预测数据[23],可以较好地验证程序的可靠性。HBS 外形的几何参数如图3 所示,其中:r=22.5 mm,θ1=5°,θ2=15°。计算来流条件与风洞试验一致,其中来流马赫数Ma∞=6.85,雷诺数Re=0.72×106(参考长度取头部直径),定姿态攻角及动态验证初始攻角分别为0°,4°,8°,13.5°,16°和20°。
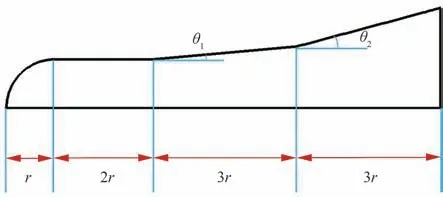
图3 HBS 模型几何外形示意图Fig. 3 Geometry of HBS model
HBS 外形静态气动力系数随攻角变化曲线如图4 所示,图中同时给出了文献[24-25]的数值结果。该模型的升阻力系数均随攻角逐渐增加,其中阻力系数先缓慢上升,而后在10°攻角附近增速加快。升力系数曲线斜率变化较小,基本上随攻角线性变化。计算所得升阻力系数与参考结果没有明显差异。
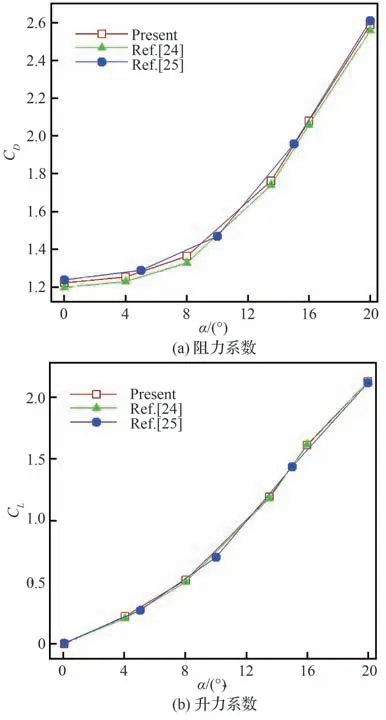
图4 HBS 外形静态气动力系数随攻角变化曲线Fig. 4 HBS static aerodynamic coefficients varying with angle of attack
以定姿态计算所得流场作为非定常模拟的初场,分别模拟0°,4°,8°,13.5°,16°和20°初始攻角条件下的强迫俯仰振荡运动,振幅均取1°,减缩频率设置为0.05。俯仰阻尼导数的计算使用基于Ektin 非定常气动力模型的强迫振荡动导数辨识方法[26]。图5(a)为不同初始攻角下的静导数计算结果,数值模拟结果与参考结果的变化趋势保持一致,随着来流攻角增加,HBS 钝锥体模型的静稳定性参数从正变为负,基本在8°攻角之后转变为静稳定状态。随着攻角继续增加,静导数符号在17°左右再度改变,静稳定性再次发生变化。数值结果与试验值[23]基本吻合;与文献[24]中的计算结果之间存在散布,静导数在小攻角和大攻角处吻合较好。图5(b)为俯仰阻尼动导数随初始攻角的变化情况,模拟结果与参考结果基本一致,HBS 标模均处于俯仰动态稳定状态。当来流攻角小于13.5°时,动导数变化较小,此后动导数迅速增加。在13.5°攻角附近结果与试验值[23]存在一定差异,此处流动复杂需要进一步研究。
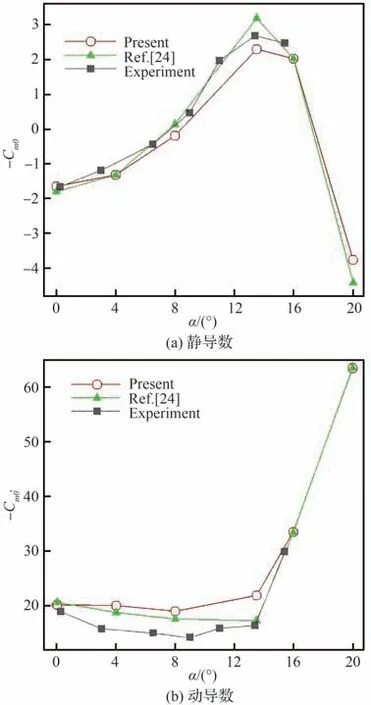
图5 静导数及动导数随初始攻角变化曲线Fig. 5 Static and dynamic derivatives varying with initial angle of attack
综上所述,程序模拟结果基本和试验数据[23]以及文献中的计算结果[24]相符合,说明所采用程序具备了非定常问题的求解能力,可以较好地模拟高超声速飞行器动态运动问题。
2.2 网格无关性分析
针对图1 所示物理模型,选取3 套不同密度网格进行网格无关性验证,3 套网格所对应的壁面第1 层网格高度及网格雷诺数见表2。来流马赫数为5.75,其余条件见1.1 节。

表2 飞行器壁面第1 层网格高度设置Table 2 First layer height of aircraft wall
壁面网格雷诺数的定义如下:
式中:ρ∞、v∞、μ∞分别表示来流密度、速度及黏性系数;Δx为壁面第1 层网格高度。
分别选取一方程SA 和二方程SST 湍流模型,对3 套不同密度网格进行数值模拟,所得阻力系数值与对应试验值的对比见表3。结果表明,采用2 种不同的湍流模型时,计算结果与试验值均相差很小,其中一方程SA 模型的计算结果和试验值更为接近。此外,3 套网格的计算结果相差不大,并且随着壁面第1 层网格高度的减小,阻力系数逐渐向试验结果靠近。综合考虑了计算量及计算精度之后,选取中等密度网格(即Δx=0.003 mm)及一方程SA 湍流模型开展数值模拟。
3 计算结果与分析
本节研究基于C 构型(不同减阻盘构型如图6 所示)、杆件长度与钝头体直径之比L/D=1.0、减阻盘直径与钝头体直径之比d/D=0.25 的自适应减阻盘,高超声速飞行器运动方程见式(5),初始攻角取0°,振荡幅值为20°,振荡周期为125 s。
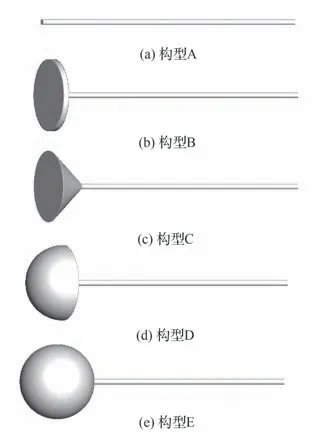
图6 5 种不同构型减阻盘示意图Fig. 6 Schematic diagrams of aerodisks of five different configurations
3.1 自适应减阻盘作用机理及动态流场
不同于固定式减阻盘,在钝头体运动过程中,自适应减阻盘始终保持对准来流方向,二者作用方式对比如图7 所示。
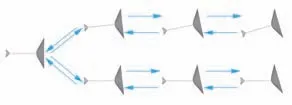
图7 固定式减阻盘及自适应减阻盘作用方式示意图Fig. 7 Principle of fixed and self-aligned aerodisks
为分析自适应减阻盘对动态机动过程中飞行器周围流场演化情况的影响,图8 给出了高超声速飞行器在1/2 周期内的对称面瞬态密度云图以及流线示意图,其中流线采用流场马赫数进行染色,可以发现,回流区、再附激波以及弓形激波共同决定着飞行器的阻力特性。如图8(a)所示,减阻杆下方回流区(以下简称“下回流区”)主要受再附激波和弓形激波相对位置的影响。随着俯仰角增加,再附激波向外偏折,在14.1°俯仰角附近已经和弓形激波共线,此时下回流区不再受到激波的限制,流动向钝头体后方扩散。尽管如此,在弓形激波的保护作用下,壁面免于来流直接冲击,因此压力依然处于较低水平。
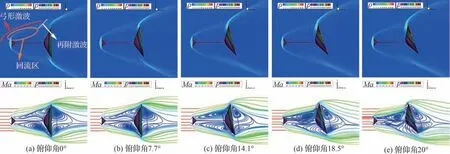
图8 加装自适应减阻盘飞行器对称面瞬态密度云图及流线示意图Fig. 8 Transient density contours and streamlines of aircraft symmetry plane with self-aligned aerodisks
对于减阻杆上方回流区(以下简称“上回流区”),在自适应减阻盘的作用下,其面积变化较小。0°俯仰角和7.7°俯仰角时,上回流区面积较大,钝体上表面整体处于上回流区包覆之中,壁面压力水平基本不变。在14.1°俯仰角时,受上壁面推动,上回流区跨过减阻杆向下运动;此时弓形激波向下偏折,导致再附点前移,钝头体肩部附近壁面压力上升。自适应减阻盘的存在使得弓形激波形状得以保持,在20°俯仰角时,减阻盘仍然可以将再附点控制在钝体肩部附近。20°俯仰角之后,回流区又开始逐渐恢复原状。
3.2 自适应减阻盘和固定式减阻盘对比
当采用2 种不同的减阻方式时,高超声速飞行器在机动过程中的阻力系数时间历程曲线如图9 所示。在图示的2 个振荡周期中,采用自适应减阻盘方法之后,80%以上的大部分时间范围内,飞行器阻力系数大幅下降。而在0°俯仰角附近,自适应减阻盘的阻力系数略大于固定式减阻盘,此时二者相对于基准飞行器(图1)的减阻率均比较高。
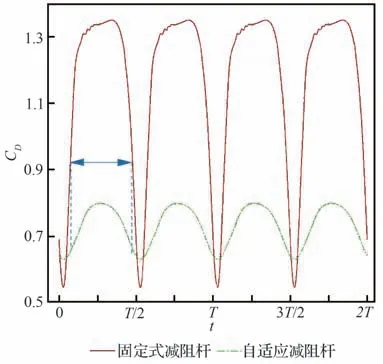
图9 阻力系数时间历程曲线对比Fig. 9 Comparison of drag coefficients varying with time
图10和图11 分别为飞行器在20°俯仰角瞬时的回流区示意图和对称面流线图,其中图10 沿轴向对流场做剖面处理,各剖面均给出了马赫数云图,从中可以观察到回流区的大致形状。
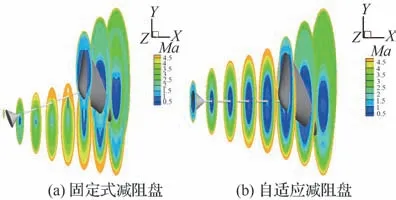
图10 20°俯仰角瞬时回流区示意图Fig. 10 Recirculation zone at pitch angle of 20°
结合图10 和图11 可以看出,当高超声速飞行器机动至20°俯仰角时,由于来流可以直接越过杆件,导致固定式减阻盘重构流场作用下降。而自适应减阻盘始终对准来流,因此杆件上下两侧流场对称性更强,在回流区的保护下,有效降低了飞行器所承受的压差阻力。
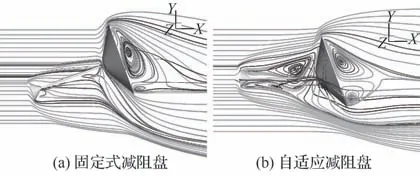
图11 20°俯仰角瞬时对称面流线图Fig. 11 Streamlines of symmetry plane at pitch angle of 20°
3.3 不同参数对自适应减阻盘动态减阻效果的影响
本节采用控制变量的研究方法,通过非定常数值模拟,分别改变减阻盘构型、杆件长度以及减阻盘直径等参数,探讨自适应减阻盘在高超声速飞行器动态机动过程中减阻效果的变化情况。飞行器的具体运动形式见1.2.2 节。
3.3.1 减阻盘构型
首先针对安装不同形状减阻盘的高超声速飞行器,对比研究其在动态机动过程中的阻力特性。图12 为不同减阻盘构型对应的飞行器阻力系数和升阻比随攻角变化曲线。
如图12(a)所示,构型A 在动态机动过程中阻力系数变化较大。其中,当飞行器“抬头”(攻角:0°→20°、0°→-20°)时,阻力系数较小;“低头”(攻角:20°→0°、-20°→0°)时,阻力系数相对较大,最大、最小阻力系数均出现在±6°俯仰角左右。另外4 种减阻盘构型对应的飞行器在“低头”时的阻力系数同样要高于“抬头”过程,不过差别较小,最大阻力系数出现在±20°俯仰角附近。按照飞行器阻力系数大小,5种减阻盘构型可排序为:构型A>构型D>构型E>构型B>构型C。
图12(b)为飞行器的升阻比变化曲线,其中,T表示飞行器的俯仰振荡周期。在0°俯仰角(0、T/2、T)附近,由于飞行器上下对称,其升力系数接近0,5 种构型的差别较小。不同形状减阻盘的主要差别在20°俯仰角(T/4、3T/4)左右,构型C与构型E 的升阻比十分接近,并且小于其余三者,另外3 种构型按升阻比大小可排序为:构型B<构型D<构型A。
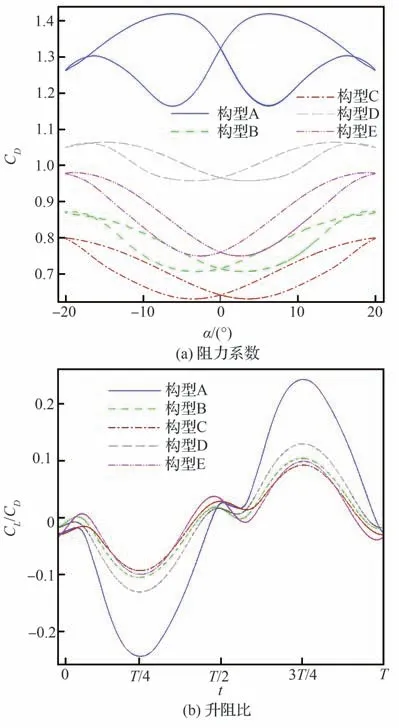
图12 不同减阻盘构型对应的阻力系数及升阻比曲线Fig. 12 Drag coefficients and lift-to-drag ratios of different aerodisk configurations
5种不同减阻盘构型作用下0°俯仰角瞬时钝头体壁面压力系数分布如图13 所示,其中y>0 部分代表轴线上方壁面,y<0部分表示轴线下方壁面。
显然,上下壁面存在一定的压强差,在0°俯仰角时为飞行器提供了微弱的升力。图13 中同时给出了基准飞行器在0°俯仰角时的壁面压力分布,可以看出,在回流区覆盖之下,钝体顶点附近壁面压强大幅度下降。在钝头体肩部,受弓形激波和流动再附等共同作用,壁面压强远高于驻点处。相对基准飞行器,构型C、构型B 以及构型E 依然能够降低肩部壁面压力,说明这3 种减阻盘构型的回流区面积较大,可以覆盖到钝体肩部,其中构型C 作用效果最佳。
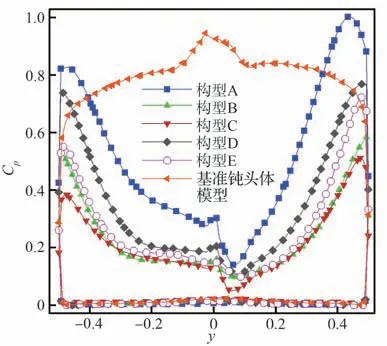
图13 0°俯仰角瞬时钝头体壁面压力系数分布Fig. 13 Pressure coefficients of wall at pitch angle of 0°
随着俯仰角增加,钝头体迎风面压强逐渐上升,背风面由于处于弓形激波之后,压力系数相对较低。20°俯仰角瞬时钝头体壁面压力情况如图14所示,其中构型A 压力系数分布与基准飞行器差别较小,为0.4左右。在其余4种头部构型作用下,背风面压力系数可以下降至0.2 以下,下降率可以达到50%以上,按压力系数大小排序为:构型C≈构型B<构型E<构型D。由于流动再附等原因,壁面压力系数峰值出现在迎风面钝头体肩部附近;后体压力系数相对较小,且基本不受减阻盘形状影响。
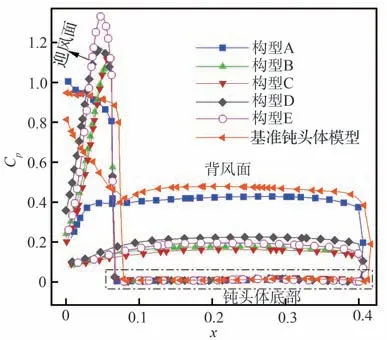
图14 20°俯仰角瞬时钝头体壁面压力系数分布Fig. 14 Pressure coefficients of wall at pitch angle of 20°
3.3.2 减阻杆长度
图15 给出的是加装不同长度减阻杆的高超声速飞行器在一个周期内的阻力系数变化情况。
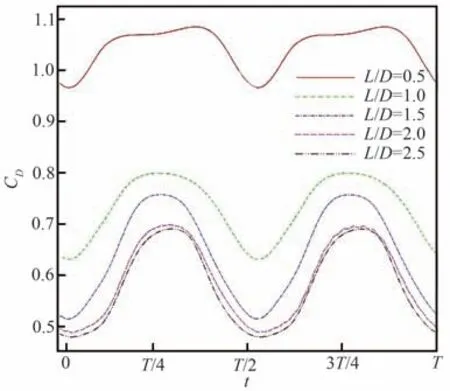
图15 阻力系数时间历程曲线Fig. 15 Drag coefficients varying with time
结果显示,在整个振荡周期内,飞行器的阻力系数均随着减阻杆长度增加而下降。其中当L/D从0.5 上升至1.0 时,阻力系数下降幅度最大,而L/D=2.0 和2.5 两种构型之间差距相对较小。
由图16 可知,在其余参数相同的情况下,随杆件长度增加,钝头体前方壁面压力水平明显下降,压差阻力逐渐减小。当L/D从0.5 增加至1.0 时,钝头体前方回流区尺寸逐渐增加,因此图15 中L/D=0.5 和L/D=1.0 构型对应飞行器的阻力系数差别较大。此外,随着L/D继续增大,减阻杆头部附近开始出现二次小回流区(L/D=1.5,2.0,2.5),不过由于二次回流区距离钝体壁面较远,对壁面压力影响较小。钝体前方大回流区面积也有增加,但变化较小,其中L/D=2.0 和2.5 时较为接近,因此L/D=1.0 之后加装不同长度杆件对飞行器阻力系数的影响不大。
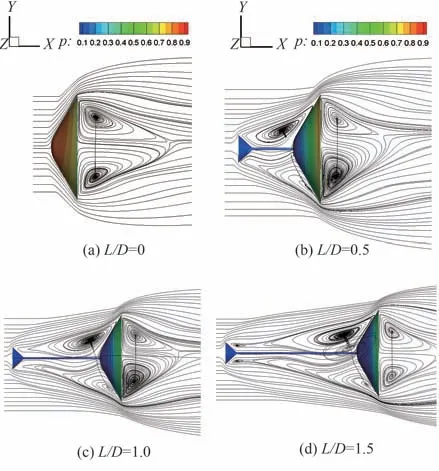
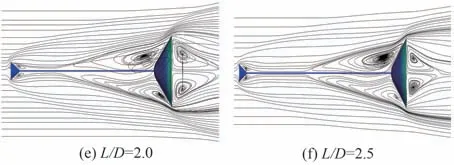
图16 0°攻角瞬时流线及壁面压力云图Fig. 16 Streamlines and wall pressure contours under angle of attack of 0°
3.3.3 减阻盘直径
当减阻盘直径不同时,高超声速飞行器在俯仰振荡过程中的阻力系数变化情况如图17 所示。不难发现,增大减阻盘直径有利于改善飞行器机动过程中的阻力特性,不过随着减阻盘尺寸增加,这种改善作用逐渐趋于饱和,即当减阻盘直径为0.312 5D和0.375D时,飞行器对应阻力系数曲线逐渐靠近。
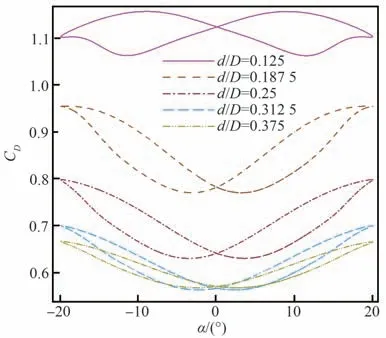
图17 阻力系数随攻角变化曲线Fig. 17 Drag coefficients varying with angle of attack
此外,d/D=0.125 时,最大阻力系数出现在±10°俯仰角附近,最小阻力系数出现在±12°俯仰角左右。其余4 种尺寸减阻盘对应的阻力系数的最大值和最小值则分别对应±20°及0°俯仰角。
如图18 所示,在减阻盘肩部,高速气流的方向会发生偏折,其上方形成一个膨胀扇面,Kharati-Koopaee 等[27]详细解释了这一现象。随着减阻盘直径增加,膨胀扇尺寸以及倾角随之增大,分离激波向外扩展,弓形激波波后影响范围扩大,因此不难理解“随减阻盘尺寸增加,阻力系数逐渐下降”的变化规律。
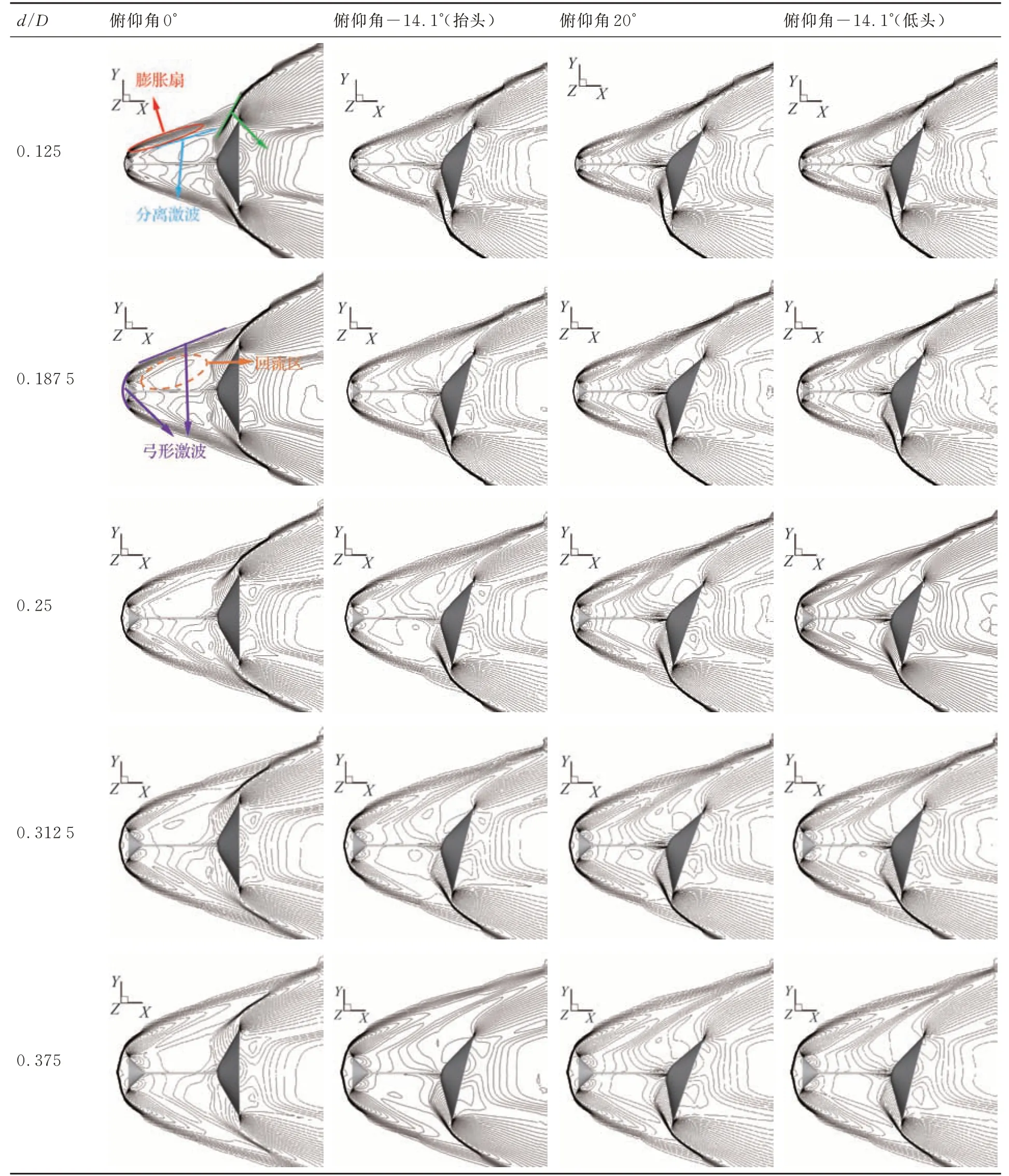
图18 不同俯仰角瞬时压力等值线图Fig. 18 Transient pressure contours at different pitch angles
观察0°攻角时的等压力线云图可以发现,由于俯仰振荡过程中存在迟滞现象,流场关于减阻盘轴线并不完全对称。当d/D=0.312 5 时,分离激波和再附激波的位置逐渐趋于共线,此时回流区的面积基本不再大幅变化,因此图17中d/D=0.312 5和d/D=0.375 对应的减阻盘构型在0°俯仰角附近阻力系数曲线接近重合。
4 结 论
针对自适应减阻盘,通过非定常数值模拟,首先探讨了其作用机理及对动态流场演化的影响,然后对比了固定式减阻盘以及自适应减阻盘的差异,并详细分析了高超声速飞行器的动态阻力特性随减阻盘构型、杆件长度以及减阻盘直径等参数的变化规律。主要结论如下:
1)当存在来流攻角时,自适应减阻盘依然可以发挥其流场重构的作用,有效地解决减阻率急剧下降的问题,有利于机动飞行。
2)相对于传统固定式减阻盘,在强迫俯仰振荡过程中,采用自适应方法后,80%以上时间中飞行器阻力系数大幅下降。并且随着俯仰角增大,自适应减阻盘相对于固定式减阻盘的优势逐渐增加。
3)在减阻盘构型、杆件长度以及减阻盘直径等参数的研究中发现,构型C 减阻效果最佳,高超声速飞行器的阻力系数随着杆件长度增加而下降,并且增大减阻盘直径有利于改善飞行器在机动过程中的阻力特性。不过随着减阻盘尺寸增加,该改善作用逐渐趋于饱和。
致 谢
感谢国防科技创新研究院的张来平老师和常兴华老师提供的指导和帮助。

