基于直线形浮标阵的反潜巡逻机监听方案

王庆江，盛 沛，单 鑫

（海军航空大学，山东 烟台，264001）

0 引言

声呐浮标搜潜系统是反潜巡逻机（以下简称“巡逻机”）对潜搜索最主要的设备之一，常被布放于任务海区，用于执行搜索、跟踪、定位和识别任务，其一般在当上级要求在短时间内以较高的发现概率迅速查明水下海域内有无敌潜艇时使用[1-3]。

实际应用中，巡逻机需要搜索的海域较大，而声呐浮标（以下简称“浮标”）的作用距离有限，因此，通常将浮标布设成某种阵形以提高其效能[1-4]，其中最基础也最常用的就是单列直线式声呐浮标阵（以下简称“直线阵”）。

对于已布设好的直线阵，有关学者[5-11]提出了巡逻机“航路平行于直线阵监听浮标”（简称“平行监听”）和“航路垂直于直线阵监听浮标”（简称“垂直监听”）2个方案，虽已取得了不少研究成果，但还有以下2个问题须要做进一步的研究。

1）飞行高度的影响。巡逻机监听直线阵的飞行区域是个三维空间，因此，必须考虑巡逻机飞行高度对其监听航路的影响。

2）巡逻机监听航路的长短问题。在直线阵已知、飞行高度已定的前提下，巡逻机监听航路的长短是否存在极限。

本文在借鉴相关研究成果的基础上，重点对上述2点进行研究和分析。

1 直线阵及其监听航路

巡逻机在直线阵上方飞行并监听浮标时，其飞行航路通常有3种方案[9-16]：1）平行监听航路方案；2）垂直监听航路方案；3）其他监听航路方案，如交叉监听航路方案（巡逻机以“8”字形航路在直线阵上方盘旋飞行并监听）。从巡逻机飞控/导航难度、航路复杂度、人员工作环境的舒适度等指标来判断，其他监听航路方案显然不如平行监听航路方案和垂直监听航路方案，因此，本文只研究前2种方案。

1.1 平行监听

平行监听是指当直线阵布设好后，巡逻机以固定的飞行高度在其上空中央沿平行于直线阵的方向循环飞行，并在飞行期间对浮标进行监听的1 种方式。巡逻机监听飞行时的高度一般保持不变，巡逻机航路所在的、距地面高度为H的平面称为（巡逻机）任务平面，将此平面分别投影于铅垂面（过直线阵）和水平面（浮标所在平面）中，可得图1。

须注意的是，任务平面的航路点在铅垂面内投影点用字母表示时，统一有下标“T”，以便与对应的水平面内投影点进行区分。

图1中：由n个同型的浮标（S1，S2，…，Sn-1，Sn）组成的直线阵长度为LF，相邻2 浮标间距离RF不大于每个浮标的作用距离（浮标在水下能发现目标时，浮标与目标之间的距离）Rf的2倍，即RF≤2Rf；浮标与巡逻机间有效通信距离是DT，其在水平面上投影为DT-S；巡逻机转弯半径、最小转弯半径分别为RZ、RZ-min，其 飞 行 航 路 关 键 点 为A→B→C→E→F→G→A，可以看出，此航路由2 个等长（长度为LSZ）直线段BC段、FG段以及2 个等长（半径为RSJ，且RSJ≥RZ-min）的半圆弧段GAB段、CEF段组成。

图1 平行监听直线阵的航路示意图Fig.1 Sketch map of parallel monitoring linear array

1.2 垂直监听

垂直监听是指当直线阵布设好后，巡逻机在其上空中央沿垂直于直线阵的方向循环飞行，并在飞行期间对浮标进行监听的1种方式。将巡逻机任务平面分别投影于铅垂面（过直线阵）和水平面（浮标所在平面）中，可得图2。

图2 垂直监听直线阵的航路示意图Fig.2 Sketch map of perpendicularity monitoring linear array

图2 中：垂直监听方案中所要监听的直线阵与平行监听方案中的直线阵相同，即LF、RF、Rf、DT都相同；DT在水平面和铅垂面上的投影分别是DT-CS和DT-CC；巡 逻 机 的 飞 行 航 路 关 键 点 为A→S→B→P→Q→C→T→D→N→M→A，它是由2 个等长（长度为LCZ）直线段MN段、PQ段以及2 个等长（半径 为RCJ，且RCJ≥RZ-min）半 圆 弧 段MASBP段、QCTDN段组成。

2 监听航路分析

由于巡逻机的监听航路受直线阵特点、浮标性能、巡逻机飞行高度等因素的影响，因此，对于已布设好的直线阵，规划巡逻机监听航路的最基本原则就是在任意监听时刻，尽可能地使巡逻机都能监听到全部浮标。

2.1 一些问题说明

1）巡逻机飞行区域问题。通过图1、2可以看出，通常巡逻机以定高、匀速的姿态飞行来监听浮标。巡逻机如果要与浮标保持通信，它只需位于以浮标为球心、以DT为半径的半球体内即可。巡逻机要想在任意时刻与直线阵中的所有浮标都能通信，只需位于以浮标S1和Sn为球心、以DT为半径所形成的半球体的交集内即可。以监听期间“是否都在此交集内”为标准，巡逻机有2 种飞行方案，一是按文献[10]所述的“巡逻机部分时间段在交集内飞行”的方案。由文献[5][7]可知：使用浮标反潜时，有可能预知/预估潜艇的位置和速度，这时文献[10]的方案可行；但也存在“不但不知潜艇的信息，连搜潜区域内是否存在潜艇都不确定”的可能性，这时还要预估潜艇的速度进行反潜是不可取的，因此，该方案具有局限性。二是“巡逻机全部监听时间都在交集内飞行”的方案[8-9,11]。采用此方案，无论搜潜区域内有无潜艇，无论是否知道/预估潜艇的位置和速度，都能保证有相同的发现（潜艇）概率，而且能保证“任意监听时刻巡逻机都能监听到全部浮标”，故本文采用此方案。

2）监听航路的有效监听长度问题。如图1、2 所示，在满足监听要求的前提下，通常监听航路是由直线段和曲线段组成，并且在飞行全程中都对浮标进行监听。考虑到：①巡逻机的飞控和导航设备的精度；②转弯期间对反潜设备的影响（如振动）；③频繁转弯操作增加了人员的疲劳感；④战术安排或其他原因。因此，文献[11]提出了“少转弯多飞直线的观点并且只考虑飞直线期间而不考虑转弯期间的监听问题”，这导致了计算模型和结论的不同，故文中采用“巡逻机多飞直线，少转弯并且在飞直线期间和转弯期间都要考虑监听问题”的观点，即巡逻机的全程飞行航路都是有效监听航路。

3）直线阵的有效长度问题。由图1、2可知，直线阵的实际长度是浮标S1与浮标Sn之间的长度LF。但是，考虑到如果有潜艇在与浮标S1或浮标Sn的距离不大于Rf的区域内通过时，浮标可以发现潜艇（巡逻机发现潜艇），因此，认为直线阵的长度为LF+2Rf也是合理的。对于同一个直线阵得到“2 种长度”，是因为考虑问题的角度不同，在文中认为直线阵的有效长度是LF。

4）可以用发现潜艇的概率（发现概率）作为巡逻机监听直线阵搜索效能的指标[8-9,12]，这是1个可行的指标，文中不进行重复研究。

5）直线阵的长度LF、RSJ（RCJ）确定后，反过来可以推算出直线阵中浮标的数量或者反推直线阵的最大长度LF-max，方法见文献[10]所述，这也是1 种可行的方法，文中不进行重复研究。

6）巡逻机进行监听时，当战术要求（直线阵长度、监听高度、监听时速度、监听时间）和巡逻机的性能指标（最大/最小飞行速度、最大/最小飞行高度、留空时间、最小转弯半径）已知时，在满足少转弯多飞直线的前提下，巡逻机飞行1圈时的航路长度，在一定程度上反映了飞行方案的优劣。因此，文中在给出通用飞行方案的计算方法的前提下，也研究了几种特殊的监听航路。

2.2 平行监听航路分析

在直线阵长度LF和飞行高度H已确定的前提下，分析巡逻机的平行监听航路。

2.2.1 通用监听航路分析

按1.1节所述方法，得到任务平面在铅垂面（过直线阵）的投影和在水平面（浮标所在平面）的投影后，将水平面内的关键航路点投影到铅垂面内，可得图3。显然，部分航路点重合。此外，由图1、3可知，要满足任意监听时刻巡逻机都能监听到所有浮标：对于浮标S1，巡逻机飞行时不能超过点ET；对于浮标Sn，巡逻机飞行时不能超过点AT，即只要巡逻机在区间ATET内飞行，在任意监听时刻巡逻机都能监听到所有浮标。

图3 平行监听航路在铅垂面内投影Fig.3 Projection of parallel monitoring route in vertical plane

由图1、3可得：

即：

由图1、3可知，巡逻机执行监听任务时，单程的实际飞行路径长度Lall-S为：

由式（2）（3）可知，LSZ和RSJ是2 个相互影响的变量，只要确定其中1个变量的值，则另1个变量也可确定。此外，由式（2）（3）可知，巡逻机的飞行高度与其单程飞行路径长度成反比。

2.2.2 特殊监听航路方案

当LSZ和RSJ分别取特殊值时，可以得到几种特殊的监听航路。

2.2.2.1 转弯半径最短的平行监听航路方案

由图1、3，式（3）可知，当直线阵长度LF和飞行高度H已知时，巡逻机按照“直线段的长度最短（LSZ=0）、转弯半径也最短（RSJ=RZ=RZ-min）”的方案绕圈飞行时（见图4），可得最短监听航路Lall-S-min：

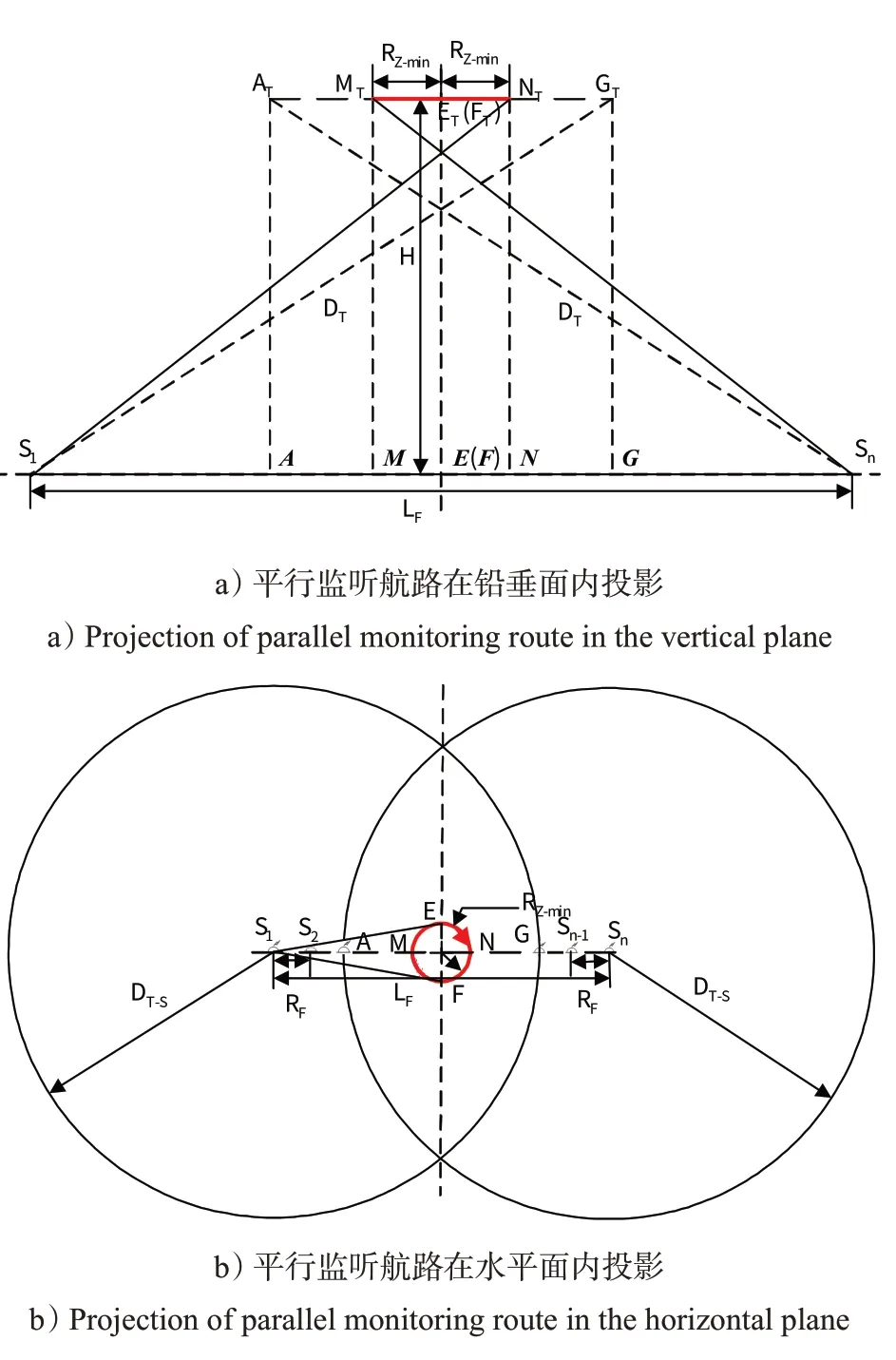
图4 航路最短方案的航路示意图Fig.4 Sketch map of the shortest route scheme

由图4可得：

显然，巡逻机按最短平行监听航路飞行时，巡逻机与直线阵中任意浮标的距离不大于S1NT，也不大于DT，此方案可行。

2.2.2.2 直线段最长的平行监听航路方案

当LF、H已知，巡逻机按最小转弯半径(RSJ=RZ-min)绕圈方案飞行时的航路与图1 b）、图3 类似。由式（2）（3）可知，这时巡逻机的直线段长度LSZ-max、单程的实际飞行路径长度Lall-S-max-1为：

2.2.2.3 转弯半径最长的平行监听航路方案

当LF、H已知，巡逻机航路没有直线段(LSZ=0 )，按最大转弯半径(RSJ=RSJ-max＆gt;RZ-min)绕圈飞行时，可得转弯半径最长的平行监听航路方案，如图5所示。

图5 转弯半径最长的航路示意图Fig.5 Sketch map of the route with the longest turning radius

此时的S1NT(DT)、S1MT(AT)、S1ET(FT)的计算方法与2.2.2.1节类似，并且已知巡逻机与直线阵中任意浮标的距离不大于S1NT，也不大于DT。

由LSZ=0、式（2）（3）可得巡逻机的RSJ-max、单程航路长度Lall-S-max-2为：

2.2.3 4种方案监听航路长度的比较

由4种监听航路的定义及式（4）与式（3）（7）（9）比较可知，2.2.2.1节所述的“转弯半径最短的平行监听航路方案”在4种方案中监听航路最短。

比较式（3）与式（7），由于RSJ≥RZ-min，因此，2.2.1节所述的通用的平行监听航路方案的航路长度不小于2.2.2.2 节所述的直线段最长的平行监听航路方案的航路长度。

将式（9）与式（3）相减，并将式（2）变形代入，得：

由上式可知，2.2.2.3节所述的“转弯半径最长的平行监听航路方案”的航路长度比2.2.1 所述的“通用的平行监听航路方案”的航路长。

因此，上述4种监听航路方案的长度关系是：

2.3 垂直监听航路分析

在直线阵长度LF和飞行高度H已知的前提下，分析巡逻机的垂直监听航路。

2.3.1 通用监听航路分析

按1.2 节所述方法得到任务平面在铅垂面（过直线阵）的投影（图2 a））和在水平面（浮标所在平面）的投影（图2 b）、图6 a））后，将水平面内的关键航路点投影到铅垂面内，可以得到图6 b）。

图6 垂直监听直线阵示意图Fig.6 Sketch map of perpendicularity monitoring linear array

垂直监听航路的一些要求与平行监听航路类似，在此只对浮标Sn进行分析，其他浮标情况类似。

由图2、6可得：

由图2、6可知，巡逻机执行监听任务时，单程的实际飞行路径长度Lall-C为：

由式（13）（14）可知，LCZ和RCJ是2个相互影响的变量，确定其中1个变量的值，则另1个变量也可以确定。此外，巡逻机的飞行高度与其单程飞行路径长度成反比。

2.3.2 特殊垂直监听航路方案

2.3.2.1 转弯半径最短的垂直监听航路方案

由图2、6，式（14）可知，当直线阵长度LF和飞行高度H已知时，当LCZ=0、RCJ=RZ-min时，巡逻机存在最短监听航路Lall-C-min：

垂直监听时的最短航路示意图，如图4所示，其与水平监听时的最短航路情况类似，相应结论也可以通用，在此不重复。

2.3.2.2 直线段最长的垂直监听航路方案

当LF、H已知，与2.2.2.2 节的方案类似，巡逻机按最小转弯半径(RCJ=RZ-min)绕圈飞行时，这时巡逻机监听航路的直线段的长度最长(LCZ-max)。此方案的航路与图6 b）类似，也可参见图7 中绿色线所示航路。由式（13）（14）可知，这时巡逻机直线段长度(LCZ-max)、单程的实际飞行路径长度Lall-C-max-1为：

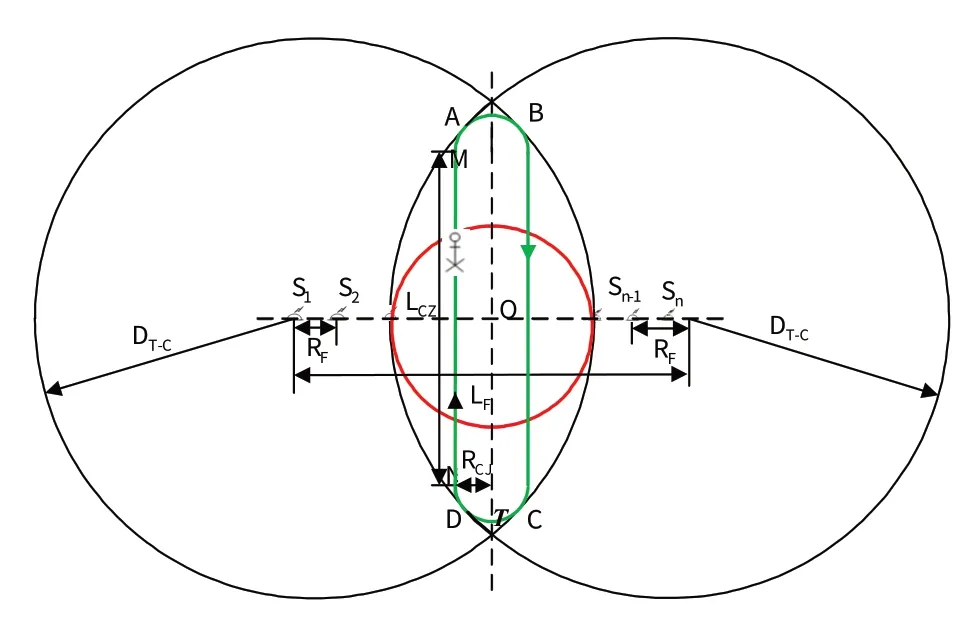
图7 直线段最长方案与转弯半径最长方案航路比较示意图Fig.7 Sketch map of route comparison between the scheme with the longest straight section and the scheme with the longest turning radius

2.3.2.3 转弯半径最长的垂直监听航路方案

当LF、H已知，与2.2.2.3节的方案类似，巡逻机航路没有直线段(LCZ=0 )、按最大转弯半径(RCJ=RCJ-max＆gt;RZ-min)绕圈飞行时，可以得到转弯半径最长的垂直监听航路方案，见图7 中的红线航路所示（也可参见图5b））。由式（13）（14）可知，这时巡逻机最大转弯半径RCJ-max、单程的实际飞行路径长度Lall-C-max-2为：

2.3.3 4种方案监听航路长度的比较

由4种监听航路的定义及式（14）（15）（17）（19）比较可知，2.3.2.1节所述的“航路最短的垂直监听航路方案”在4种方案中监听航路最短。

由式（14）（15）（18）中各值的定义及图7可知：

由上式可知，式（14）在其定义域内存在极大值RCJ-Z。使用MATLAB 对式（14）进行绘图，其中，DT=40 km，H=2 km，LF=50 km，RZ-min=4 km，RCZ的定义域见式（20），可得图8。

图8 式（14）的仿真图Fig.7 Simulation diagram of equation 14

2.4 其他情况分析

除了2.2节、2.3节分析的巡逻机监听航路的情况，还须要注意以下几点。

1）2.2节、2.3节分析巡逻机监听航路的前提多是巡逻机航路在“以浮标S1和浮标Sn为球心、以DT为半径所形成的半球体的交集内”，且部分航路在“交集”的边界上。这只是为了分析在极限条件下的航路情况，实际上也可以将航路适当收缩到“交集”内，相应的公式不变。例如，在LSZ已确定的条件下使用式（2）求解RSZ后，可将实际值选取为不大于解算出的RSZ（但必须保证RSJ≥RZ-min）。

2）当巡逻机按最小转弯半径飞行仍不能保证其航路在“交集内”时，可以选用多架巡逻机共同完成任务或降低高度飞行。

3）上文讨论巡逻机监听航路时，其飞行高度固定。实际上，巡逻机监听时的飞行高度是可变的，且高度越低，“交集”的区域越大，巡逻机单次飞行的航路可以越长。

3 仿真分析

3.1 仿真条件

设浮标按文中1 节所述的直线阵布设，下面对巡逻机按2节、3节中所述的平行监听和垂直监听2个方案进行仿真并分析。仿真时，假设条件如下：

1）巡逻区域及浮标阵：巡逻区域是1 个海峡，已按直线阵方案被布设了1 道长50 km 的浮标阵，浮标声呐的作用距离Rf=2 km，浮标与巡逻机的监听距离DT=40 km，相邻浮标间距离RF=1.7Rf。

2）巡逻机模型：巡逻机的最小转弯半径RZ-min=4 km，巡逻机的飞行高度H=0～6 km。

3）监听方案：巡逻机分别按平行监听方案和垂直监听方案飞行并监听浮标。其中，H=2 km，LSZ=LCZ=10 km。

3.2 仿真结果

根据3.1节所述条件及式（2）～（8）、式（13）～（19），得到了飞行的仿真航路图（与图1、2 类似），相应仿真参数见表1所示。

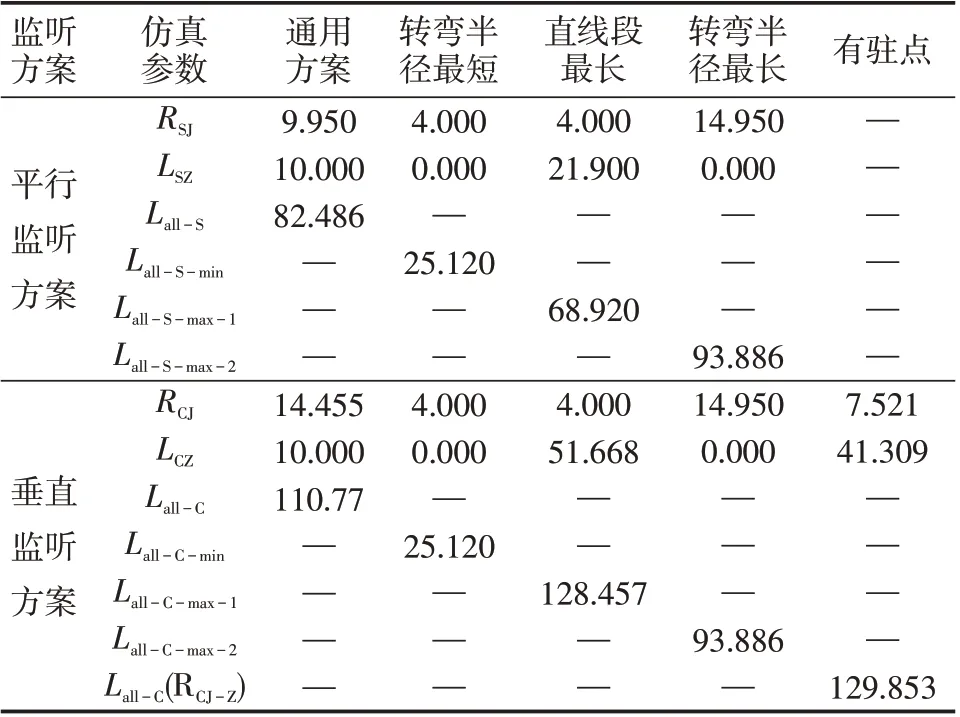
表1 2种监听方案的仿真结果Tab.1 Simulation results of two monitoring schemes单位：km

3.3 结果分析

根据表1中的仿真参数及图1、2，可得如下结论。

1）2种方案都能完成监听直线阵的任务。

2）水平监听航路的长度（3～6 行）符合式（11）结论；垂直监听航路的长度（9～13行）符合式（19）结论。

3）从“通用方案”“直线段最长”方案可知，同等条件下，垂直监听航路的长度大于水平监听航路的长度。从图1、2 中也可得到类似结论：由于要在“交集”内飞行，而“交集”的任务平面在水平投影的外形类似长度大于宽度的“橄榄球”，因此，在满足条件的前提下，垂直监听航路（在“橄榄球”的长度方向飞行）大于水平监听航路（在“橄榄球”的宽度方向飞行）。

4）从“转弯半径最短”、“转弯半径最长”方案可知，同等条件下，只进行转弯飞行时，垂直监听航路的长度与水平监听航路的长度一致。从2.2.2.1 节、2.3.2.1 节分析可知，此情况下的航路由巡逻机的性质（转弯半径）决定；从2.2.2.3 节、2.3.2.3 节分析可知，此情况下的航路由巡逻机性质（转弯半径）、直线阵的性质（浮标的通信距离）决定，因此，2种转弯飞行方案的航路长度一致。

4 结束语

本文首先分析了其他学者的研究成果并给出了本文的研究前提和基础；然后，详细分析并讨论了巡逻机执行监听飞行时的平行监听航路方案和垂直监听航路方案，提出并研究了4种特殊的监听飞行方案；最后，通过仿真对4 种方案进行了验证并对仿真结果进行了分析，其结果可为巡逻机在实际中更好地执行航空反潜任务提供理论基础。