基于Kriging与多点取样算法的压气机特性建模

徐竟耕，曾 力

（重庆交通大学机电与车辆工程学院，重庆 400074）

作为航空燃气轮机的基本部件，压气机对空气的流通运送起着至关重要的作用，其功能为：先对空气进行减速增压，再向燃烧室里不断输入高压空气，以提高气流的膨胀功，使整个发动机系统的热效率得到增强[1-2]。流量系数不仅是衡量压气机空气流通能力的重要指标，也是直接影响燃气轮机数字化建模精度的重要参数。当计算流量系数时，需要根据已知的燃气轮机实验数据来建立插值模型，但实验数据的获取成本却较高。因此，如何利用有限的实验数据，借助合适的建模方法构造出高精度的插值模型便成为最值得研究的问题之一[3-4]。

目前的压气机特性建模方法都存在对流量系数的预测精度不高的问题[5-6]。为了优化插值模型，提高预测精度：陈辉等在Kriging 插值法的基础上，建立了符合压气机流量特性的插值模型，探索了相关模型和参数初值的选取对最终结果的影响[7]；尹大伟、李本威等根据压气机的流量特性和效率特性，在原有模型基础上进行了重新构造[8]；Ghorbanian K and Gholamrezaei M等通过实验发现，虽然BP神经网络对压气机特性的预测效果较好，但却难以确定合适的网络结构，最终导致出现“欠拟合”或“过拟合”的现象[9]；涂环、赵勇和李本威等选择了QPSO 算法，在Kriging 相关模型的基础上，在全局寻找最优参数[10]，通过该方法，优化了基于梯度的模式搜索法，使其不再须要考虑参数初始值。

上述方法虽都可提高计算压气机流量系数的模型精度，但却未考虑到Kriging 插值模型的不足，即样本库里的换算转速与待预测数据的换算转速的数值相差较大时，是无法得到高精度计算结果的。另外，这些方法也未考虑在到利用设计空间中样本点的分布与模型精度的关系来提高预测精度的同时节省样本点。

因此，本文采用了1 种基于垂距的多点取样算法。将垂距、预测标准差等参数作为筛选标准，再结合高斯函数，筛选出更具有代表性的样本点，以此建立Kriging插值模型，该算法可以在全局和局部范围内提高模型精度。实际结果表明，使用该方法构建模型时，需要的样本点数减少近30%。待预测数据与样本库的换算转速不同时，对比传统Kriging 插值模型，精度提升近10%。

1 Kriging插值法

Kriging插值法是通过对样本赋予权重，通过加权线性组合的办法对目标估值，同时满足无偏估计要求，且满足估计方差最小[11]。结合压气机特性，建立Kriging插值模型，首先定义输入与输出向量。

输入的样本向量如下：换算转速为

增压比为

输出的样本向量如下：

流量系数为

换算转速和增压比作为模型输入，记为

对应的模型输出为流量系数，记为

模型的输出与输入变量可表示为[12]

式（6）中：fT(x)β是回归模型，被称为定性漂移；fT(x)是p阶线性多项式的回归模型集合，f(x)=[f1(x)f2(x)…fp(x)]T；β是 回 归 模 型 系 数，β= [β1β2…βq]|p×q。回归模型的理论概念为在设计空间上的全局近似。多项式的阶次大多数情况下选择为0阶（常数）模型[13]。

z(x)为一随机函数，且满足：

式（8）中：R代表相关系数矩阵；矩阵中的元素r是衡量2 个不同的样本点之间距离的函数，它用来表征输入变量之间的空间相关性，即：

式（9）中：N为输入变量中元素的个数；xki、xkj分别是输入向量xi、xj的第k个分量[14]，k＝1,2,…,N；Rk(θk,dk)为相关函数，常用的相关模型有球状模型、指数模型、线性模型和高斯模型。本文选择高斯函数来确定输入变量之间的相关性，其形式如下[15]：

将式（6）代入式（5），所以模型输出向量根据计算可以表示为：

式（11）记为：

设待估计点为xnew，则待估计的输出点为：

c为样本点的权重向量，由于无偏估计要求，所以E[ŷ(xnew)-y(xnew)]=0，通过构造拉格朗日算子，代入式（14），可得估计值及回归系数β*的表达式，即：

式（15）中，γ*=R-1(Y-Fβ*)。

估计值的方差为：

2 基于垂距的取样算法

在选点的过程中，首先需要全局寻找不确定性较大的数据点[16]，还须要结合曲线特征，精确地反映曲线的曲率大小。基于垂距的多点取样算法便考虑到了以上2点[17]。选择样本曲线上的某1个单点，计算该点与相邻2 点连线的垂距，通过判断垂距大小的方式来完成初步选点，再结合预测不确定性的思想，进行第2次筛选。在换算转速相同的情况下，每1 个增压比都会存在1 个与之对应的流量系数，即它们之间存在一一对应的关系，所以，在保持换算转速不变的情况下，可以只根据增压比和流量系数来计算垂距，进而将原本的三维样本空间简化为二维样本空间。在计算之前，要根据现有的样本数据建立初始样本点集{ }O和基础点集{M}，建立Kriging 插值模型来判断点集{O}是否满足目标精度，然后再使用取样算法对{M}进行选点，筛选出的样本点组成1个新的样本点集{ }A，将点集{ }A加入到初始样本点集{ }O中。重复以上步骤，一直往初始样本点集{ }O中加点，直到Kriging 插值模型能达到预期的精度要求。基本流程图，如图1所示。

Synthesis, properties and industrial applications of amino acid surfactants 12 5

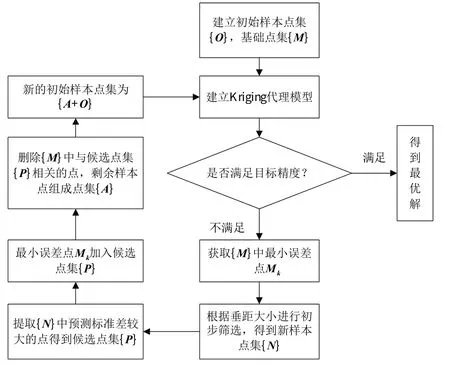
图1 基于垂距的多点采样算法流程Fig.1 Flow chart of multipoint sampling algorithm based on vertical distance

步骤1：在某一相同的换算转速nm下，压气机增压比和流量系数之间的关系是一一对应的，即有

其中，t表示在这一换算转速下，流量系数与增压比的样本数量。m为换算转速的样本数量。建立初始样本点集{ }O，则剩余的样本点组成点集i=0,1,2,…}。使用当前的点集来建立Kriging 插值模型，提取出误差最小的点Mk。集合M的式子为：

步骤2：依次检测当前换算转速下的样本点的数量是否大于等于3。如果是，则当前换算转速下的所有样本点进行步骤3；如果否，则对下一个换算转速下的样本点数量进行检测。

步骤3：连接Mi-1，Mi+1，计算点Mi到Mi-1Mi+1连线的距离D。式（19）为D的计算公式：

D值的高低能够准确地体现曲线在这一点的弯曲程度，找到合适的垂距阈值d，检测D与d的大小关系。如果D＆gt;d，进行步骤4；如果D＆lt;d，进行步骤5。

步骤4：将Mi以及该换算转速下的首尾2 点提取到另一新建空点集{N}，进行第5步。

步骤5：将Mi在点列中后移1个点，进行步骤3。

图2中：a）为基础点集{M}组成的图形；b）代表以垂距作为判断标准的选点；最后被选取的点组成的点集{N}，如c）所示。将c）与a）进行比较，可以看出留下的样本点大部分都是能够反映原始曲线特征的样本点。

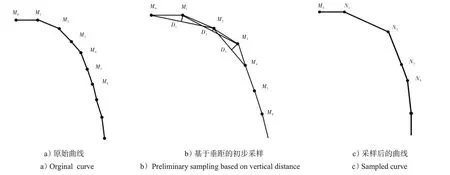
图2 基于垂距的曲线采样方法示意图Fig.2 Schematic diagram of curve sampling method based on vertical distance

阈值d的选择没有明确的计算公式，也与样本点集无关[18]。所以,本文在考虑阈值的取值时，采用迭代法来寻找最佳阈值。

首先，根据样本点的垂距判断阈值的取值范围。

然后，再取多个合适的初始阈值，并设置一定的间隔，间隔的取值范围取决于不同样本点的垂距之差。判断每一次迭代的选点数以及最后计算结果的精度：如果在选点数为“0”的情况下依然没有达到目标精度，则须更换初始阈值或者阈值间隔，以进行下一次迭代；如果达到目标精度，则记录计算结果并进行下一次迭代。

最后，将得到的计算结果进行比较，以筛选出最佳阈值。

根据上述流程，筛选出了能够体现原始曲线图形特征的样本点。为了预测不确定性，须使用Kriging插值模型计算点集{N}中各点处预测值的标准差，将标准差按式（20）进行再次筛选，筛选后得出的点便构成了候选点集{P}。

把先前所计算出的误差最小点Mk加入到{ }P里，接下来寻找{M}中与{P}相关的点并将它们去除，此步骤需要使用高斯相关函数。选取合适的判断标准值，根据计算出的相关函数R与标准值进行比较，以此判断是否相关。删去{M}中与{P}相关的点以后，将剩余的点提取到1个新的样本集{A}中，加上初始样本{O}，最终样本点集为{A+O}。

3 仿真验证

将换算转速相同的样本点记为1 组样本，现有某型燃气轮机压气机流量系数样本共15组[19]，每组有10个样本点，一共150个样本点。

随机选取1组样本为待验证样本，剩下的14组作为训练样本，进行随机抽取3 次。分别将原始样本点和基于垂距的多点取样算法筛选后的样本点作为Kriging插值模型的输入。待验证的3组样本点，如表1所示。

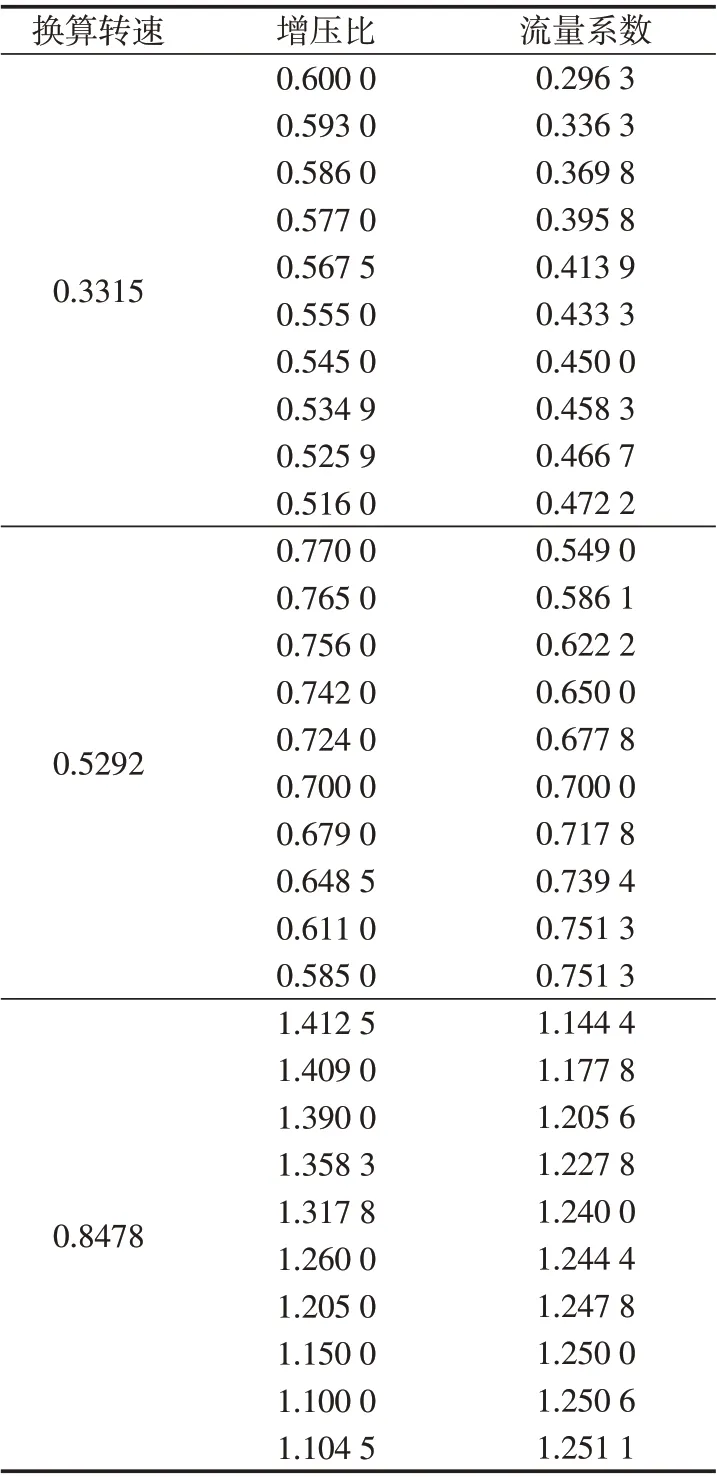
表1 待验证样本点Tab.1 Sample points to be validated

首先，从14组训练样本中的每组随机抽取1个样本点（除首尾2 点），建立初始样本点集{O}。剩余的126 个样本点则组成基础样本点集{M}，在此初始基础样本点集{M}中搜索误差最小解，得到点Mk。

只有在同一换算转速下且样本点满足数量大于等于3 的条件时，才计算垂距。这样便降低了原本样本空间的维度，可以简化计算公式，提升计算效率。依次检测给定换算转速下的样本点的数量，并设置好垂距阈值d、相关函数R等初始参数。

开始对待验证样本点进行预测，表2 是对3 组待验证样本点的预测过程与结果。

预测第1 组待验证样本点，选取换算转速等于0.331 5 的样本点组，根据垂距的大小，选取的垂距阈值d依次为0.001 和0.001 5，b取值为0.1 和0.2，相关函数R判断标准分别为0.000 1 和0.000 1，加点次数为2次，加点个数分别为76和11。

预测第2 组待验证样本点，选取换算转速等于0.529 2 的样本点组，根据垂距的大小，选取的垂距阈值d依次为0.001和0.002，b取值为0.35和0.45，相关函数R判断标准分别为0.1和0.2，加点次数为2次，加点个数分别为75和35。

预测第3 组待验证样本点，选取换算转速等于0.847 8 的样本点组，根据垂距的大小，选取的垂距阈值d依次为0.001、0.001 5、0.002 和0.002 5，b取值分别为0.1、0.2、0.3 和0.4，相关函数R判断标准分别为0.000 1、0.000 12、0.000 14 和0.000 16，加点次数为4次，加点个数分别为74、10、4和3。

最后，验证选点后的模型精度，并与选点前的Kriging 插值模型进行比较。用均方根误差（Root mean square error，RMSE）和最大绝对误差（Max absolute error，MAE）这2 项指标来验证，判断全局精度和局部精度，均方根误差公式为[20]：

式（21）中：m为1 组验证样本（1 条等换算转速曲线）中样本点的个数；ŷ为预测值；yi为实际值。

图3 为流量系数插值示意图，黑色曲线为流量系数的实际值。可以看出，相比选点前的Kriging模型的插值精度，选点后的Kriging模型预测值的红色点更靠近代表实际值的黑色曲线。表3是2种方法结果的精度检验。可以看出，对3组样本进行预测后，使用本方法的RMSE和MAE，都有明显降低。

图3 流量系数插值示意图Fig.3 Schematic diagram of flow coefficient interpolation

表3 误差比较Tab.3 Comparison of errors

当换算转速为0.847 8时，选点后的模型相较于选点前的模型精度有较大提高。造成这种结果的原因是该换算转速下的样本点过于冗杂，在对曲率较小的曲线部分进行预测时容易受到其他多余样本点干扰。而选点后的模型使用的样本点都具有代表性，这便淡化了多余样本点带来的负面影响，有效解决了此类问题。

4 结论

为了提高航空燃气轮机流量系数的插值建模精度，同时也为了减少使用样本的数量，在传统Kriging代理模型的基础上，采用了基于垂距的多点取样算法。首先，根据垂距来删除多余冗杂的样本点；然后，使用预测标准差与高斯相关函数来判断样本点的相关性；最后，只筛选出具有代表性的样本点，以此来提高Kriging插值模型精度。仿真表明，该选点方式有效可行，且具有以下特点：

1）采用该取样算法选点后，Kriging 模型针对单目标点的插值精度得到了明显的提高；

2）该算法能够选出最优点，并删除与之相关的点，节省了构建模型时所需要使用的训练样本数量；

3）选出的点能够与原始曲线形状相适应，提高了全局精度和局部精度，进而提高了计算效率。