双机协同无源定位算法

康 旭，王德江，张 涛

（1.中国科学院长春光学精密机械与物理研究所航空光学成像与测量重点实验室，吉林 长春 130033；2.中国科学院大学，北京 100049）

随着网络技术的发展，分布式被动探测系统、无线传感器网络等探测体系已在军事领域得到广泛应用。与其相关的多站信息融合和联合定位目标问题也得到了深入研究。分布式无源定位系统利用载机观测到目标的到达角（Angle of Arrival，AOA）来估计目标位置[1-8]。双机协同能在较广泛的区域内利用传感器获得目标方位数据，实现对目标的定位。角度测量值是目标位置的非线性和非凸函数，不能直接求解；且测量值受噪声干扰，对目标的定位精度会产生很大影响。可以利用统计学知识对定位误差进行分析，研究出更有效、鲁棒性更强、定位精度更高的定位算法。

无源定位过程中，获得目标AOA 测量值的常用方法是在载机上使用红外探测系统或天线阵列。目前，利用AOA 测量值进行目标定位已经得到广泛研究。基于AOA 测量，Stansfield 首先推导了1 种基于AOA 的单站定位方法[9]；Nardone 等建立了基于极大似然原理的估计方法（Maximum Likelihood，ML），提出了理想估计器的概念，并给出了克拉美罗下界（Cramer-Rao Lower Bound，CRLB）的估算方法[10]；Torrieri等提出了协同定位的经典极大似然估计方法[11]；Motti等对比分析了最大似然估计器与Stansfield 估计器的性能[12]；Allen 等提出1 种伪线性估计算法（Pseudolinear Estimation，PLE），并给出最小二乘解，但存在偏差的问题[13]；Kutluyil发展了偏差减小的伪线性估计（Bias Reduced Pseudolinear Estimation，BRPLE）并建立了1 种渐进无偏的加权工具变量估计器[14]；Alba 等提出了纯方位目标定位的最小二乘算法（Least Squares，LS），并给出其封闭形式的解[15]；Sohn等利用三角测量对目标进行定位[16]；Sharma等假设目标高度为0，对地面运动目标进行定位，并通过扩展卡尔曼滤波提高定位精度[17]；Cheng 等通过两点相交定位对地面目标进行定位，并使用最小二乘迭代提高定位精度[18]。

以上方法针对的是地面目标的定位，并不能用于远距离空中目标。Bai 等提出1 种改进的交叉定位算法，提高对远距离空中目标的定位精度[19]；Sun等给出了1种基于改进极坐标系的纯方位定位算法的特征向量解[20]。

上述基于AOA 测量的算法研究，让我们更加看好双机协同定位的发展前景，但针对不同场景如何选择定位算法仍困扰着我们。本文从基于最小二乘法的定位算法和基于最大似然估计理论的定位算法两方面来分析目标定位理论，并使用MATLAB对不同误差条件下的目标位置估计的均方根误差（Root Mean Square Error，RMSE）进行对比，从多个角度对比不同场景下算法的性能。

1 基于纯角度信息的双机定位模型

如图1 所示，2 架无人机si=[xi,yi,zi]T(i=1,2 )，协同定位辐射源u=[x0,y0,z0]T。每架载机观测到的AOA与辐射源位置间的关系如下：

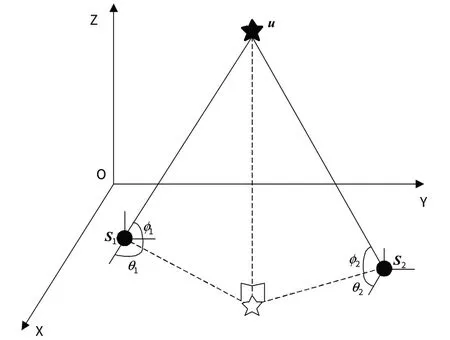
图1 AOA定位模型Fig.1 AOA localization model

式（1）中，θ0i和ϕ0i分别表示辐射源相对载机的方位角和俯仰角真值。

实际中，AOA测量值不可避免地受到噪声干扰：

式（2）中，测量噪声nθi和niϕ是服从均值为0，方差分别为σ2θ和σ2ϕ的独立高斯白噪声。

2 基于AOA测量值的定位方法

载机一般通过携带的GPS确定自身实时位置，结合辐射源的AOA 测量值通过三角测量法估计辐射源位置。受噪声干扰的测量值会导致估计误差，利用统计学理论可以有效减小误差。下面介绍基于最小二乘法和极大似然估计法的定位方法。

2.1 最小二乘类定位方法

对式中的反正切函数变形得到辐射源与测量值的关系可表示为：

将所有载机的测量按式（3）的形式堆叠成矩阵：

2.1.1 普通最小二乘法

普通最小二乘法考虑了受噪声影响的测量值对向量b的影响，通过忽略高阶噪声项的泰勒展开，近似得到向量真值为b0=b-eb，其中，eb表示残差。

通过最小化残差平方和

可得辐射源位置坐标为：

2.1.2 加权最小二乘法

普通最小二乘法认为测量值对结果的影响具有一致性，但实际中，方位角和俯仰角的测量噪声方差不同。因此，不同噪声的测量值对结果的影响权重不同。若已知噪声nθi和niϕ的统计分布，可得测量角噪声协方差矩阵为

与普通最小二乘法相似，利用最小化残差平方和

可得辐射源位置坐标为：

2.1.3 总体最小二乘法

如前所述，普通最小二乘法一般认为向量b受测量噪声影响。但式中A和b都由测量值得到，应等价看待它们。令A0和b0分别为观测矩阵和观测向量真值，通过泰勒展开将观测矩阵和观测向量真值分别表示为A0=A-E和b0=b-e，其中E和e为误差项。对此，同时引入校正向量Δb和校正矩阵ΔA，对b和A内存在的误差进行补偿，以抑制噪声对辐射源定位精度的影响，从而实现有误差的矩阵方程求解向精确矩阵方程的求解的转换：

此时，总体最小二乘问题可用约束最优化问题来表示：

方程解为增广矩阵[A,b]的最小奇异值对应的右奇异向量，也就是[A,b]T[A,b] 的最小特征值对应的特征向量。

2.2 最大似然类定位方法

尽管最大似然估计受初始值的影响存在局部最优的问题并具有较大的计算复杂度，但由于其渐进无偏性，故常作为性能比较的基准。在高斯噪声假设条件下，方位角和俯仰角测量的似然函数是1 个多元高斯概率密度函数：

式（14）中，J是最大似然代价函数：

2.2.1 高斯-牛顿迭代法（GNIM）

一般使用高斯-牛顿迭代法求解ML 估计问题。对于没有封闭解的非线性最小二乘估计问题式，迭代步骤如下：

式（16）中：u(k)是第k次迭代值，利用简单的算法或先验知识可以得到；e(u)=Ψ-ψ(u)，J(k)是u估计值为u(k)时的Ψ(u)的雅可比矩阵

一般按式（16）迭代2～4次即可得最优解。

2.2.2 加权工具变量伪线性估计法（WIVPLE）

在小噪声假设下，采用伪线性估计使最大似然代价函数线性化，线性化过程利用2 个二次代价函数分离方位角和俯仰角：

式（18）中，uxy=u(1 ∶2 )，uz=u( 3)。

由式（18）我们可以发现：代价函数J1(uxy)只取决于方位角测量；而代价函数J2(uxy,uz)同时取决于方位角和俯仰角。我们将J的最小化求解过程分解2 步：首先，通过最小化J1(uxy)，解得uxy；然后，将其代入J2(uxy,uz)，再通过最小化J2(uxy,uz)，解得uz。

在小噪声假设下，(θi-θi(u) )和(ϕi-ϕi(u)) 近似为0，可表示为：

式（19）中，sxy,i=si(1 ∶2 )。

式（15）近似为：

由于式（20）求和项中第1项的分母项未知，将其去除后问题简化为：

同理解得式（20）求和项中第2项：

由于上述对数似然函数线性化过程中引入了误差，影响辐射源位置的估计精度。线性矩阵等式为，误差项分别为其估计偏差主要是由F和η间的相关性引起，因此，可通过修改式来消除：

目标位置估计值为：

式（24）中，工具变量H基于目标的初始状态参数估计构造，即是利用目标位置估计值得到的方位角。

2.2.3 克拉美罗界（CRLB）

确定任何无偏估计量的方差下限在实际中非常重要，它揭示了所讨论的模型中，估计结果的均方根误差下限或估计精度上限。根据似然函数式（15）有：

此外，可通过Fisher信息矩阵（FIM）计算得到：

式（26）中：J0是目标在真实位置处的雅可比矩阵；K是噪声协方差矩阵。

3 仿真实验

为直观比较算法优劣，本节我们利用蒙特卡洛数值模拟进行仿真实验。目标定位精度的仿真结果用RMSE表示，其计算方式为:

式（27）中：u是源位置的真值；ûi是第i次仿真得出的u估计值；L=1 000 是蒙特卡洛实验次数。

此外，我们使用CRLB 根作为性能评估的基准。ML 是渐近无偏的，但需要迭代和接近真实源位置的初始值。在实际中，目标的真实位置是未知的，在此我们以普通最小二乘法的解作为ML迭代初始值。

场景1：按图1建立笛卡尔坐标系，设置2种几何构型。固定载机到目标间距都是10 km，其中：较好几何构型设置目标相对两载机的张角为90°；较差几何构型设置目标相对两载机的张角为45°∘。较好几何构型中载机位置分别为s1=(1 0,0,0.8 )km 和s2=( - 10,0,0.8) km，辐射源位置坐标( 0,10,1) km；较差几何构型中载机位置分别为s1=(1 0,0,0.8) km 和s2=( 0,10-10 2,0.8 )km，辐射源位置坐标( 0,10,1) km。为了便于分析，本文忽略了载机的位置误差，并且令方位角和俯仰角的测量误差服从均值为0，标准差分别为2ρ和ρ的高斯分布。如图2所示，当载机与目标间的几何构型不同时，目标的定位精度也不同。

图2 瞬时定位仿真结果Fig.2 Simulation results of instantaneous localization

图2 a）和b）分别描述了较好几何构型与较差几何构型在ρ的标准差从0.5°∘～5°∘的范围内，目标位置的定位精度变化趋势。

显然，较好几何构型可大大提升定位性能。在小误差范围内，这些算法性能都能接近CRLB，且定位精度相差不多，随着角度测量误差增加，目标的定位精度降低。当几何构型较差时，算法间的优劣更加明显。图2 b）得出：ML类的算法中，以普通最小二乘法估计结果作为初值的高斯-牛顿迭代法定位精度最高，但是需要迭代，其计算复杂度较高；加权工具变量伪线性估计不需要迭代计算，但定位精度较低；LS 类算法中，加权最小二乘法考虑了不同测量值的权重，定位性能最高，且LS类算法计算复杂度相对ML类算法具有天然的优势。因此，我们应该根据定位性能和计算复杂度的需求选择合适的算法。

下面对载机对目标持续观测的场景下进行仿真。

场景2：在场景1 的前提下，设置载机s1速度为( 0.24,0.24,0 )km/s；载机s2速度为( 0.24,0.24,0 )km/s。角度传感器采样频率为50 Hz，令载机对目标连续观测1.5 s，其余参数设置同场景1。

如图3所示，当载机与目标间的几何构型不同时，目标的定位精度不同。

图3 持续观测定位仿真结果Fig.3 Simulation results of continuous observation and localization

与图2相比，由于可利用测量值增多，目标定位精度增加。图3 a）和b）分别描述了较好几何构型与较差几何构型在ρ的标准差从0.5°∘～5°∘的范围内，目标位置的定位精度变化趋势。

显然，较好几何构型可大大提升定位性能。与瞬时定位不同，较好几何构型的持续观测场景中，ML类算法的定位性能降低，且其计算复杂度随着测量值数量增加而增大；但较差几何构型中，加权工具变量伪线性估计在测量噪声较大时具有最佳的定位性能。LS类算法始终具备较好的定位性能。此时，我们应该根据需求选择合适的定位算法，但LS 类算法具有较大优势。持续观测的目标定位精度变化趋势与瞬时目标定位精度相同，都随着误差增加而降低；但其定位精度明显高于瞬时定位，因为载机观测时间增加，对目标的观测信息增加，目标位置的定位精度显然增加。由图3可知，随着角度误差增大，ML类算法估计目标位置的精度逐渐优于LS类算法估计目标位置的精度；大多数情况下，伪线性估计目标位置的精度最低，但当载机与目标间的几何构型较差且测角误差较大时，其对目标位置的定位精度最高。因此，应根据实际需求选择合适的算法。

4 结论

本文介绍了几种基于AOA 的无源目标定位算法，并使用蒙特卡洛法进行仿真实验对比。仿真结果显示：在不同几何构型和观测条件下，随着测量噪声增大，不同算法对目标定位精度和计算复杂度不同，且不同算法间精度存在较大差异；应该根据不同的需求，选择合适的算法。