基于可靠性评估的直升机无寿易损件的寿命分析与验证

徐 宁，袁嘉伟，王君行，于向阳

（1.92522部队，辽宁 兴城，125106；2.91331部队，辽宁 兴城，125106；3.92283部队，上海，201900；4.海军航空大学，山东 青岛，266041）

0 引言

“可靠性”（reliability）通常是指产品在规定的条件下和规定的时间内，执行规定功能的能力。随着高新技术密集型作战力量不断发展，在军事领域中，已经形成了一个个高精技术密集型“兵种群”。

临清架鼓的演奏形式有两种：一是“行街”，点锣走在队伍最前列，面向演出者，从而起到指挥、协调作用。整支队伍分成大小两路纵队，大锣在中间，边走边敲。二是圆场，大锣在中间，锣围成一圆圈，点锣穿插在各鼓中间，一边行进，一边演奏。此外，如果是开阔场地，架鼓队还常在广场上与竹马、旱船、高跷等其他民间舞蹈队伍组成“圆阵”。此时，24面鼓和大锣、点锣有条不紊地分散在其他队伍之间，大家合着鼓点边走边舞，错落有致。这种由架鼓队做引领，不同演出队伍组合的形式俗称“风搅雪”。

其中，f表示气体的分布函数，一般依赖于变量x，v，t，它表示了该气体在t时刻速度为v的粒子的密度.这个方程主要描述了在非平衡状态下分布函数f随时间演化的过程.若分布函数f与位置x无关，即f仅是关于变量v，t的函数，则方程变为

直升机具备特定的旋翼驱动结构，广泛应用了复杂先进的电子仪器设备等高精技术，这决定了设备机件维修策略的不可控性[1]，也直接导致面向复杂战场态势的装备保障规律产生了诸多新的特点和不确定因素，给以可靠性检测、评估及质量控制为主体的“一线”航空机务维修保障人员的工作开展带来了一定“困难”和挑战[2]。

寿命分析与验证是装备可靠性评估的主要途径，通过对装备性能退化趋势的动态评估来预测剩余可用寿命，并给出装备的可靠性报告[3]。尤其对于直升机有些无寿易损件，虽然没有明确的使用寿命限制，但可在实际使用维护过程中，利用大量的故障时间数据进行建模与分析，依据系统的功能或可靠性结构和概率统计[4]，给出系统的故障/寿命分布模型和可靠度函数、故障分布函数、故障密度函数、故障率函数、可靠性参数（如平均寿命、平均剩余寿命、可靠性寿命）等各种可靠性指标的定量估计，从而科学掌握装备性能变化规律[5]。

准确有效的寿命分析与验证，进而掌握装备的可靠性规律是科学制定装备维修策略的基础，而合理安排装备维修活动[6]，不仅可以使装备的可靠性（完好性）水平得以保持，而且可以有效降低寿命周期维护费用。对于提高装备的可利用率、可维护性以及延长装备的寿命等具有重大的理论研究意义与军事应用价值[7]。

1 可靠性分析

1.1 可靠性数据建模与分析流程

从装备可靠性数据的统计分析中找出其故障/寿命分布的规律，是分析装备寿命和故障、预测故障规律、研究失效机理及制定维修策略的重要手段[8-9]。

从政策环境看，改革开放进入深水区，行业治理难度日益增加。物流业管理涉及部门多，协调难度大，与一体化运作、网络化经营的物流运行模式不相适应。近年来，各部门出台了一系列政策措施，但存在落实不到位、推进速度慢、地方协调难等问题。新兴物流领域出现的新问题，也对物流业治理体系和治理能力现代化提出了新课题。

4）故障率函数λ(t)

因此，对可靠性数据进行统计分析，并找出产品寿命分布的规律具有重要意义，它是进一步分析产品故障、预测故障发展、研究其失效机理及制定维修策略的重要手段。可靠性数据建模与分析流程[10]如图1所示。

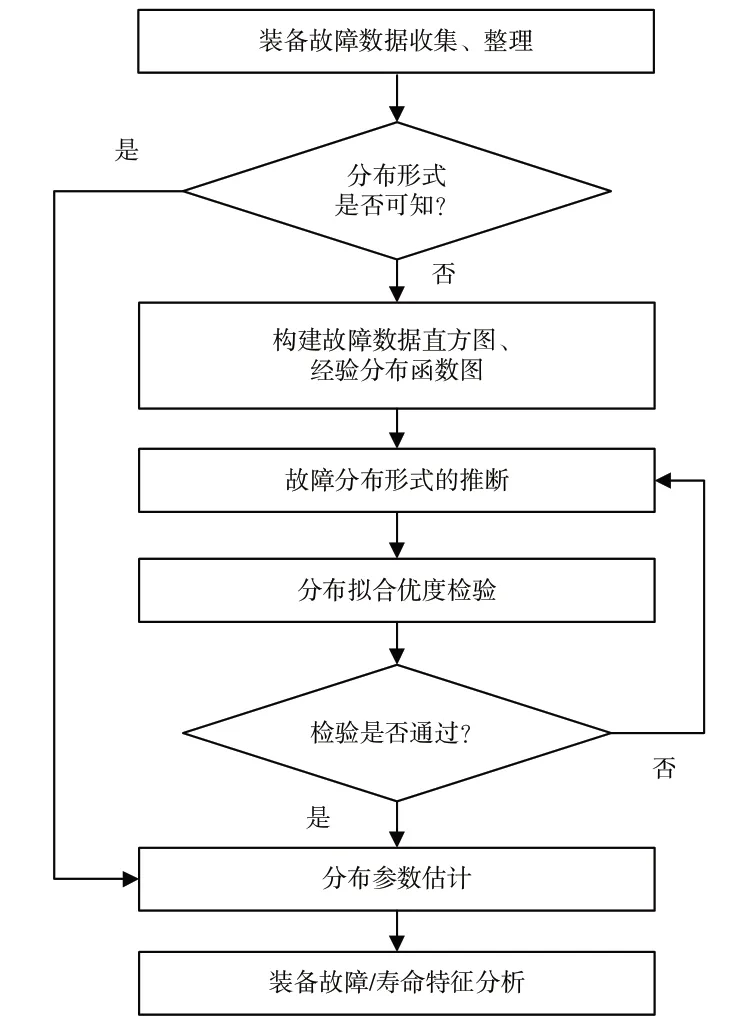
图1 可靠性数据建模与分析流程Fig.1 Reliability data modeling and analysis process

1.2 故障数据

以某型号直升机自润滑关节轴承为例，统计42件故障件发生故障前的工作时限（以下简称“工作时限”），如表1所示。根据统计的故障数据，按照可靠性数据分析逻辑图的流程，建立合适的故障分布模型，并分析该部件的可靠性寿命特征。

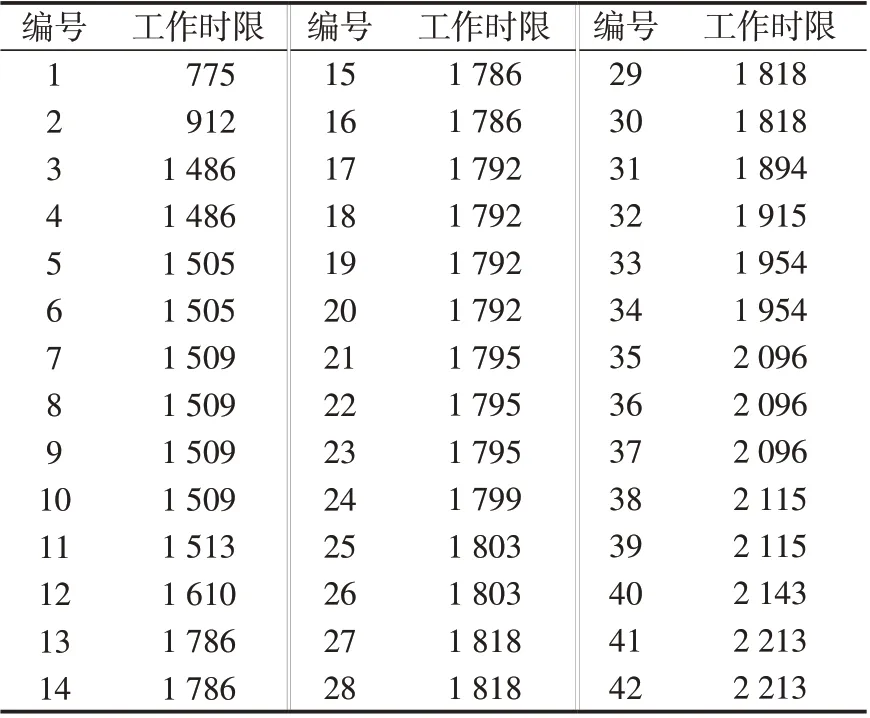
表1 自润滑关节轴承故障数据Tab.1 Self-lubricating joint bearings fault data单位：h

1.3 分布类型识别

分别添加了Weibull 分布和Logistic 分布拟合曲线的直方图，如图3、4所示。

由图2 可以看出，自润滑关节轴承故障时间分布为典型的偏态分布，很可能服从或近似服从Weibull分布或者Logistic分布。

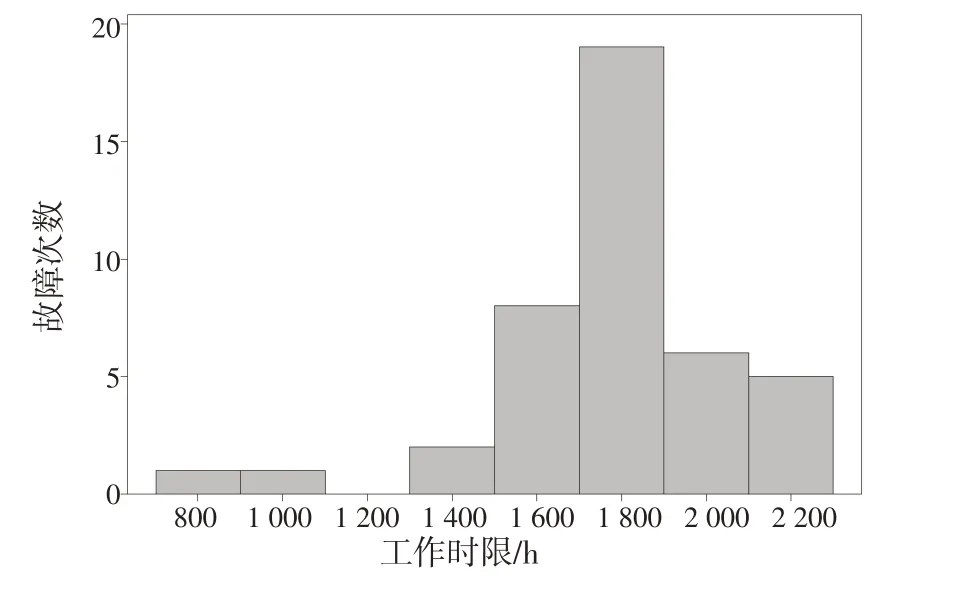
图2 自润滑关节轴承工作时限直方图Fig.2 Working time histogram of self-lubricating joint bearing

首先，根据故障数据无法直接判断分布形式，按照图1 可靠性分析流程，构建故障数据直方图；然后，依据直方图的形态来初步判断分布类型，根据表1 中的故障数据绘制的直方图，如图2所示。

通过以上公式可得阵元数为64时的相控阵探头的辐射声场，用MATLAB软件描述可得。图 10是相控阵换能器阵元数位64时的直入射声场，图11给出了相控阵换能器阵元数为64时的斜入射聚焦声场。

2016年11月，全国妇联、教育部等九部委在《关于指导推进家庭教育的五年规划（2016—2020年）》明确提出了五年内在全国普及家长学校的工作目标——城市要达到90%，农村要达到80%，让有限优质教育资源服务更多学校和社区。

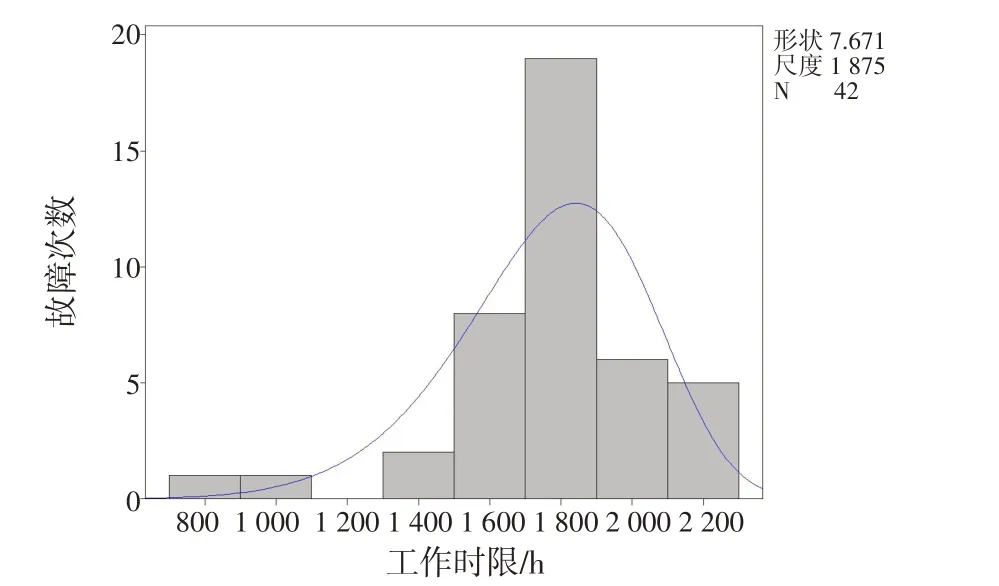
图3 工作时限的直方图与Weibull分布拟合Fig.3 Histogram and weibull distribution fitting of working time

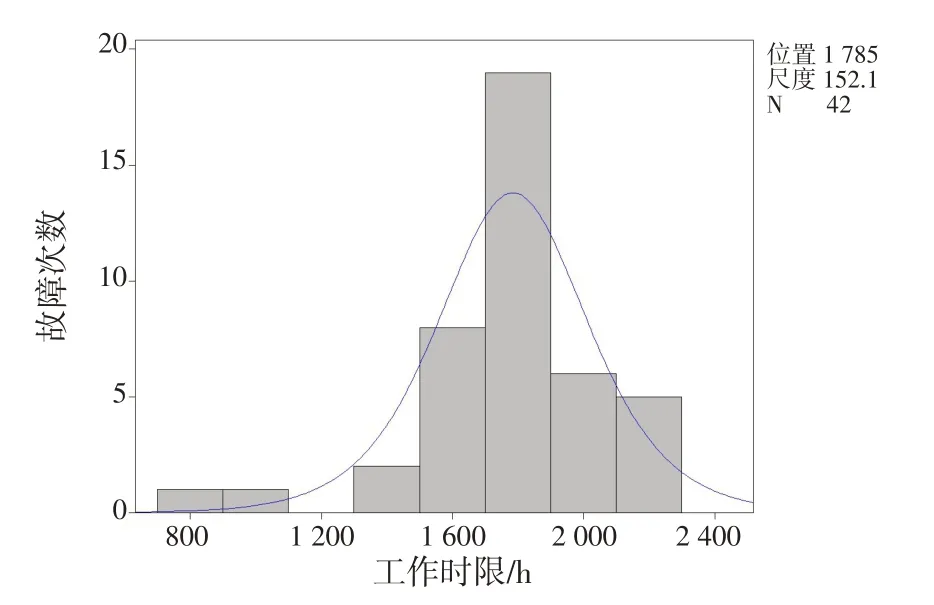
图4 工作时限的直方图与Logistic分布拟合Fig.4 Histogram and logistic distribution fitting of working time

1.4 经验分布函数图分析

使用经验分布函数图可以直观地评估故障数据分布的拟合度[11-13]，以查看针对总体估计的百分比和样本值的实际百分比，并比较样本分布。

1）定义

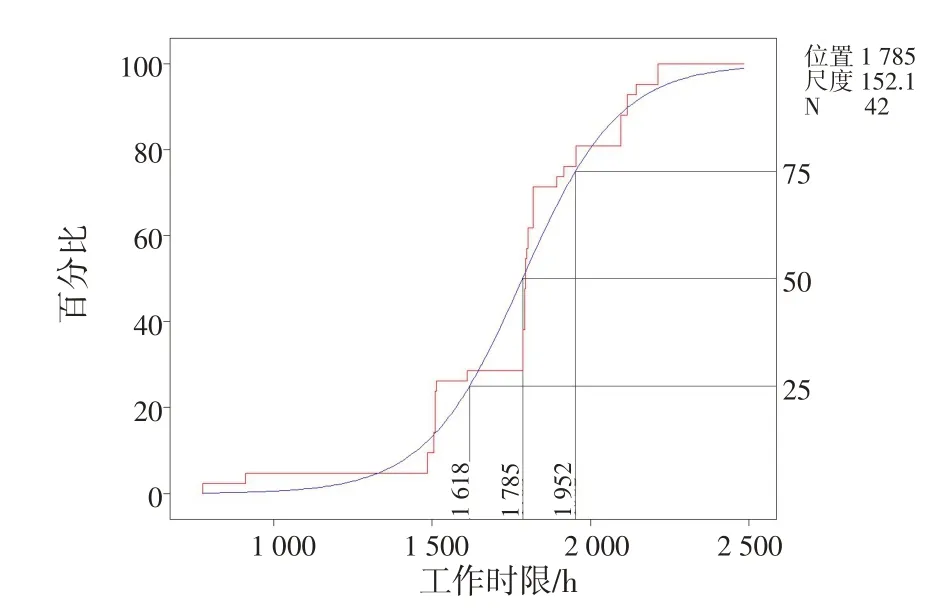
图5 数据的Logistic经验累积分布函数（标出百分比）Fig.5 Logistic empirical cumulative distribution function of data(with percentage marked)

1.5 分布拟合优度检验

为了选择最佳拟合分布，可以利用概率图比较分析。根据表1 中的故障数据，分别绘制Weibull、对数正态、指数、对数Logistic、三参数Weibull、三参数对数正态、二参数指数、三参数对数Logistic、最小极值、正态、Logistic分布等11种常见分布的概率图，采用极大似然估计法的Anderson-Darling 统计量比较[14-15]。该统计量是图点到拟合线的加权平方距离，且越靠近分布的尾部，权重越大，即Anderson-Darling 统计量越小，分布与数据拟合得越好[16]。具体如图6～8所示。

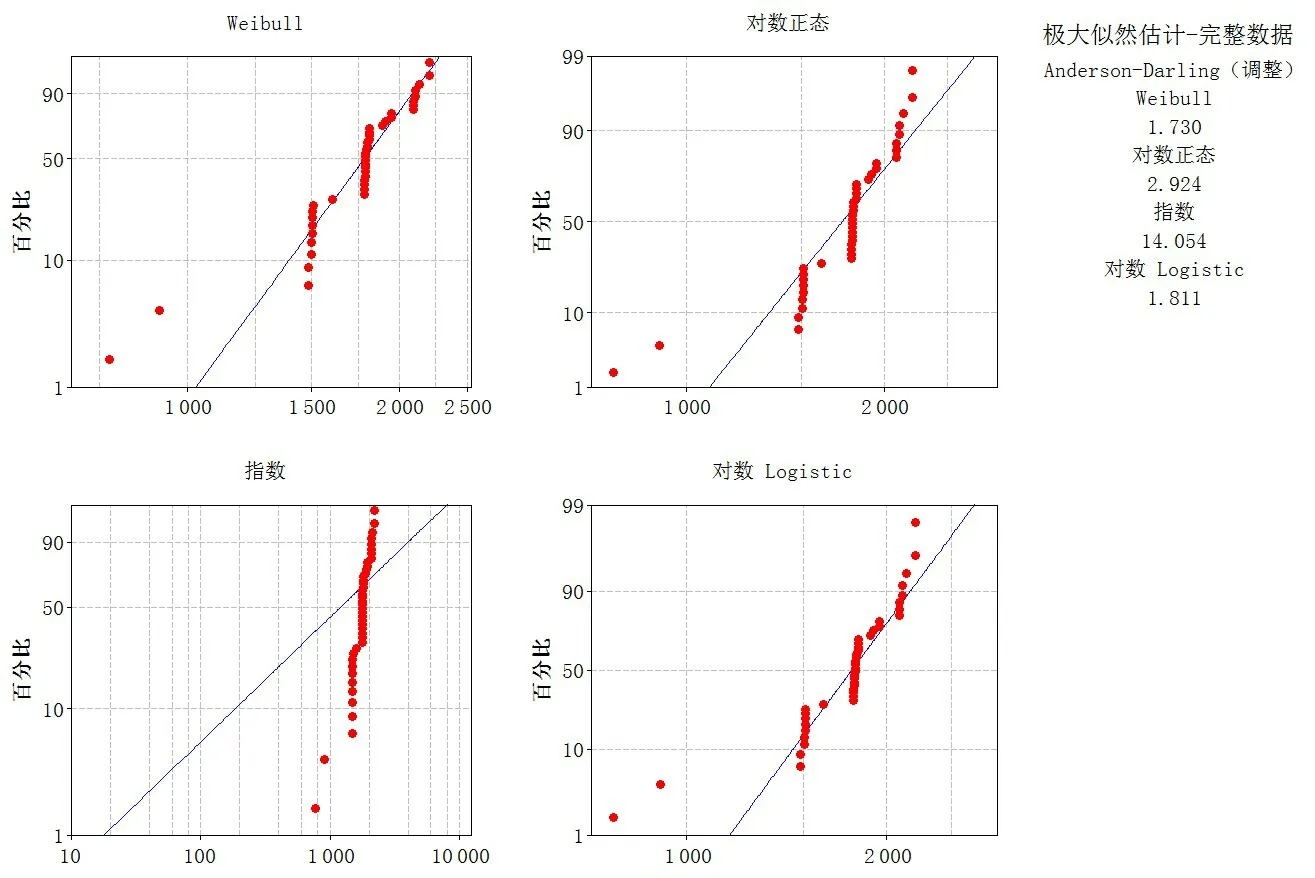
图6 Weibull、对数正态、指数、对数Logistic分布概率图Fig.6 Weibull,logistic normal,exponential,logarithmic distribution probability graphs

根据上述概率图，三参数Weibull、三参数对数正态、二参数指数、三参数对数Logistic 这4 种分布方式无法收敛于最优阈值参数。而Logistic分布的Anderson-Darling 拟合优度值最小，为1.609，因此选择Logistic分布来拟合故障数据。

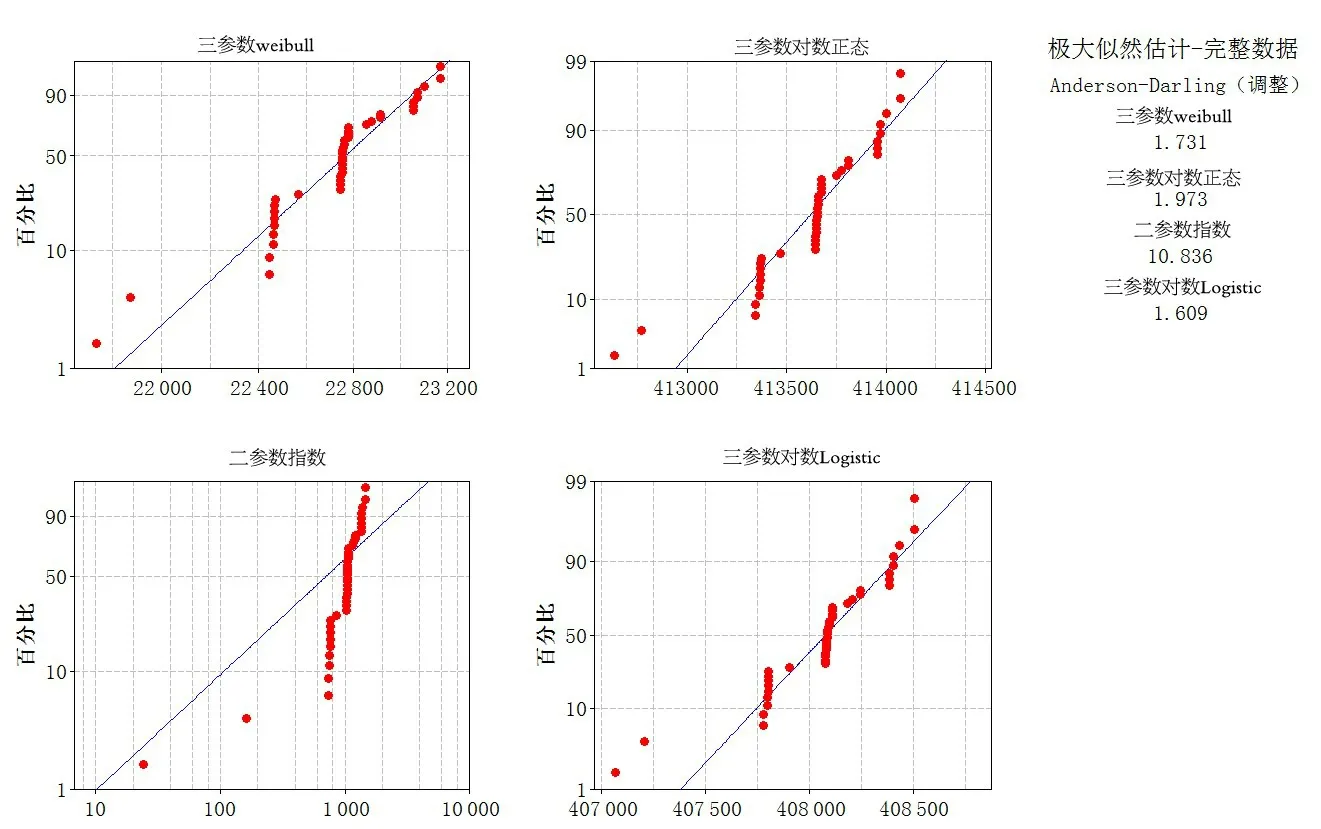
图7 三参数Weibull、三参数对数正态、二参数指数、三参数对数Logistic分布概率图Fig.7 3-parameter Weibull,3-parameter logarithmic normal,2-parameter exponential,2-parameter logarithmic Logistic distribution probability graphs

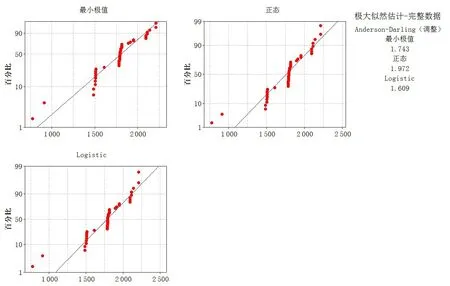
图8 最小极值、正态、Logistic分布概率图Fig.8 Minimum extreme value,normal state,Logistic distribution probability graphs

2 Logistic分布模型

绘制Logistic分布的经验累积分布函数图并标出百分比，如图5所示，图中包括中位寿命或平均故障间隔时间。步进线基本遵循拟合分布线，数据能够较好地拟合分布。

近年来，诸城市将造林绿化、美化环境作为实施乡村振兴战略的重要内容，深入开展绿满城乡五大行动，鼓励工商资本下乡造绿，持续发力经济林基地建设，促进乡村振兴。2017年，诸城拥有林地面积45万亩，林木覆盖率、城市建成区绿化覆盖率分别达到39.8%和44.6%。该市扎实推进绿满城乡五大行动，规划布局了300多个造林绿化项目，注重发挥工商资本在资金、技术、管理、人力要素的优势，示范引领特色经济林向规模化发展。

产品从开始工作到首次故障前的一段工作时间T称为寿命。由于产品发生故障是随机的，所以寿命T是1个随机变量。若连续型随机变量T的概率密度函数满足：

则称随机变量T服从参数(μ,σ)的Logistic分布[10]，记为T～L(μ,σ)。其中，-∞＆lt;μ＆lt;+∞，σ＆gt;0 是常数，称为Logistic分布的位置参数和尺度参数，μ也称为Logistic 分布的均值，σ是Logistic 分布的标准差。Logistic密度函数的形状是对称的，与正态分布的形状相似，但是Logistic分布的尾部更长或者更厚，即具有厚尾性，因此，可使用Logistic分布来建模具有更长尾部的数据操作[17]。

2）故障分布函数F(t)

2) 指标权重的确定是模糊物元评价方法的关键，其合理性直接影响结果的可信度.本文利用熵权法计算权重，充分挖掘出智慧城市建设公众参与水平评价数据中包含的客观信息，为指标权重的确定提供理论依据，有效提高权重的可信度.

3）可靠度函数R(t)

根据收集的可靠性数据，使用数理统计方法得到装备或部件的故障/寿命分布，对不同装备的可靠性数据进行参数估计；然后，再由故障/寿命分布和可靠性参数的关系，估计可靠性设计和分析中所需的各项参数（如概率密度函数、可靠度、故障率，以及各种寿命特征量等）。

5）可靠寿命tr

可靠水平为r的可靠性寿命为

6）中位寿命t0.5

利用最小二乘法和极大似然估计法进行参数估计（95%正态置信区间）。Logistic 分布的最小二乘法估计和极大似然估计的分布参数分别如表2、3所示。

3 可靠性评估

3.1 概率图分析结论

将r=0.5 代入式（5）可得中位寿命

在中国发展西洋歌剧，就必须面对许多的现实问题，由于中国的历史文化的源远流长，深入人心必然会影响西方歌剧在中国的传播。从这个方面来说，延安秧歌剧发展对我国认识西方歌剧有着很好的过渡意义，也对我国创作第一部民族歌剧《白毛女》有着先导作用。

需求计划提报不严谨，随意性较大，随意变更时间或数量，从而导致部分材料数量过高与部分材料短缺同时发生，库存积压与短缺同时存在，成本上升但却效率低下。设计变更多，实际工作中，设计变更是常态，而此时如果采购已经完成，势必造成积压。现状表明：因计划调整、设计变更、工程剩余等需求计划不准确是造成企业物资积压的主要原因。

表2 最小二乘法估计的分布参数Tab.2 Distribution parameter of least squares estimation

由此可见：最小二乘法估计法的位置μ为1 762.05，尺度σ为161.619；极大似然估计法的位置μ为1 784.95，尺度σ为152.133。从其误差来看，后者估计精度要好于前者。下面我们将采用极大似然估计法进一步对寿命特征进行分析。

3.2 分布概要图

为了直观地显示故障数据的分布情况和各种可靠性指标，现生成包括概率密度函数曲线、可靠度函数曲线、故障率函数曲线以及寿命特征统计量的故障分布概要图，如图9所示。

3.3 故障/寿命特征分析

根据以上分析，自润滑关节轴承的故障数据服从Logistic 分布L（1 784.95，40.09），即平均寿命和中位寿命均为1 784.95 h。该自润滑关节轴承的故障密度函数图，如图10所示。

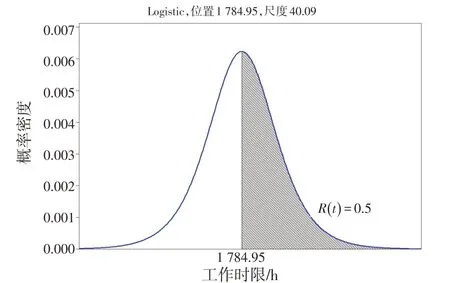
图10 自润滑关节轴承的Logistic模型密度函数图Fig.10 Logistic model density function diagramof self-lubricating joint bearing

可以看出，当自润滑关节轴承工作1 784.95 h后，其可靠性降到50%以下，应视情更换。

4 数据验证

根据自润滑关节轴承载荷谱，上海市轴承研究所参考国外轴承公司SKF 的《SKF spherical plain bearings and rod ends》中关于PTFE 衬垫的轴承寿命分析计算。按照《某型号直升机维修大纲》规定的轴向游隙为评判依据，综合考虑环境温度影响、载荷大小、工作频率等因素[18-19]，对其理论寿命进行了计算评估，其基本额定寿命Gh的计算公式为：

式（7）中：b1为负荷因数；b2为温度因数；b4为速度因数；Kp为载荷系数；Pn为载荷指数；V为平均滑动速度。经试验，将所得数据代入式（7），可得自润滑关节轴承基本额定寿命：

通过数据验证可知，自润滑关节轴承的故障数据可靠性评估得出的“平均寿命为1 784.95 h”的结论与计算评估所得额定寿命1 862 h基本一致，进一步验证了故障数据可靠性评估的可行性。

5 结束语

本文依据可靠性数据建模与分析流程，以自润滑关节轴承为例，利用Logistic 分布模型对某型号直升机无寿易损件的寿命控制情况进行分析，所得出的结论与科研部门预测的寿命基本一致。这充分证明了以自润滑关节轴承为例的无寿易损件的机械磨损为典型的退化型故障，即此类机件在使用装机过程中，性能状态随着时间的延长逐渐下降，直到达到某一阈值或在某范围内，机件彻底失效。通过对航空装备数据的可靠性分析，找出产品寿命分布的规律，是进一步分析航空装备故障、预测发展趋势、研究其失效机理及制定维修策略的重要手段，该方法可有效解决现代航空装备寿命论证的难题，在航空装备质量管理领域有较好的应用前景。