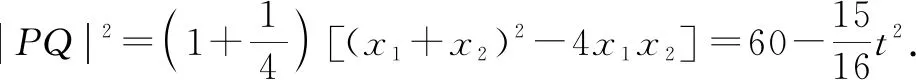对2022年上海高考数学第20题的思考

⦿上海市七宝中学 李佳伟 李 霞 管恩臣

1 前言

圆锥曲线是解析几何的核心内容，是高中数学的重点、难点，也是高考命题的热点之一.根据考纲的要求，理科对椭圆、抛物线的概念、标准方程、几何性质的要求属于掌握的内容，对双曲线是了解的内容；文科只对椭圆是掌握的内容，对双曲线、抛物线是了解的内容.纵观福建近几年的高考也可以看出这一点，椭圆是高考必考的内容，其次是抛物线，考得最少的是双曲线.其中，最值问题可以涉及中学数学各个内容的方方面面，它在高考中的地位十分突出.最值问题可以以各种知识作为背景进行考查,涉及高中数学主干知识与方法,要求考生有扎实的数学基本功及良好的数学思维能力.由此可以理解有关椭圆的最值问题在高考中的重要地位.而椭圆的参数方程因为其特点，可以把圆锥曲线的最值问题中复杂的计算转化成三角函数最值问题，从而可以大大减少计算过程和强度，是解决椭圆最值问题一个很重要且很巧妙的手段.下面笔者结合2022年上海高考数学第20题，分析参数方程在最值问题中的巧妙应用.

2 试题呈现与分析解答

图1

(1)若a=2，AM的中点在轴上，求点M的坐标；

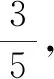
(3)若Γ上存在点P到直线l的距离为d，且满足d+|PF1|+|PF2|=6，当a变化时，求d的最小值.

分析：本题第(2)问利用直角三角形中三角比的定义能够得到a与b的关系，从而求出b的值；第(3)问的难点在于如何选参数，主要有以下几种途径.①构建点P含参数的轨迹方程；②设点P含参数的坐标；③设直线l′含参数的方程.

第(3)问的思维导图如图2所示.

图2

试题解答：

(1)由题意,得c2=2，b2=2.

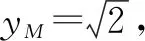
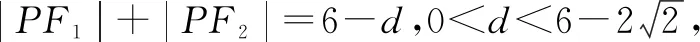
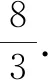
另外，本题第(3)问还有如下两种解法.

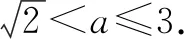
设P(acosθ,bsinθ)，则

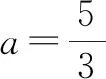
解法二：(设直线l′含参数的方程)当椭圆Γ在点P处的切线l′与直线l平行时，点P到直线l的距离d最大或最小，设此时切线l′方程为x+y+m=0.

2(a2-1)x2+2a2mx+a2(m2-a2+2)=0.

由Δ=0，得m2=2(a2-1).

从以上的解答过程可以看到，利用参数法求解，其计算量远远小于常规方法的计算量，从而提高答题的正确率.因此，在解决相关椭圆的最值问题时，可以优先考虑参数法.

3 试题延伸与推广

解：如图3，设椭圆Γ的右焦点为P(2,0)，点M在椭圆Γ的内部，直线MP与椭圆Γ交于A,B两点，则由椭圆定义可得|NF|+|NM|=8+|NM|-|NP|.

图3

由三角形的性质,得

-|MP|≤|NM|-|NP|≤|MP|.

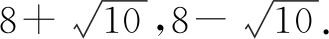
点评：变式2直接运用代数法难度较大，考虑到F是椭圆的左焦点，联想椭圆的定义，设右焦点为P，得到|NF|+|NM|=8+|NM|-|NP|，然后再利用三角形的性质解决，体现了借助椭圆定义与平面几何知识解题的特点.

图4

解：由题意，得直线AM的方程为x-2y+4=0.

设直线PQ的方程为x-2y+t=0，与椭圆Γ的方程联立，可得4x2+2tx+t2-48=0.

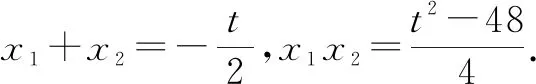
由Δ=4t2-16(t2-48)>0，得-8

点评：先借助弦长公式、两条平行线间的距离公式、勾股定理等求出|QN|2，然后再运用二次函数的性质求解，体现了函数思想.

图5

又A(-4,0)，所以直线AP的方程为

设B为直线x=-6与x轴的交点，则

点评：变式4属于多动点问题，由于P，Q两点的运动引起了点M，N的运动，因此将P设为主动点，以其坐标为参变量表示出S△APQ+S△AMN，最后借助基本不等式求得最值，体现了基本不等式的工具作用.

通过以上问题的解决，可以得到求解这类最值的两种常用思路：①从图形入手，借助椭圆的定义、三角形的性质等平面几何知识来分析；②选定参变量，表示出所求的几何(或代数)量，然后根据解析式的特点，借助导数、基本不等式、函数与三角函数的性质等知识来处理.