PBL教学法在《概率论与数理统计》课程教学中的应用
国洪松
(中国矿业大学(北京)理学院,北京 100083)
0 引言
传统的教学模式,以教师讲授为主,学生被动地接受新知识,可能会对知识背景理解不深刻,甚至感到内容枯燥,失去了自主探索的兴趣。PBL(Problem-Based Learning)教学法是一种基于问题导向、以学生为中心的教学方法,由教师提出实际问题,启发学生自由讨论,探索新知识的教学模式[1-2]。
概率论与数理统计是一门研究和揭示随机现象统计规律性的数学学科[3-6]。很多概率统计模型都有着深刻的现实背景,如等可能概型、中心极限定理、三大导出分布等,在现实生活中有着广泛的应用[7-9]。但是在以往的教学中,教师急于讲授概率论与数理统计的相关数学知识,往往把很多概念和定理结论全盘托出,而忽略了学生是否能够理解和接受;学生也以考试为目的,对相关概念和性质死记硬背,面对实际问题不会分析,不能正确建立数学模型,从而无从下手,没有办法解决。
如果在教学中能采用PBL教学法,将抽象的课程知识和实际问题相结合,启发学生自主探索,建立数学模型,用数学知识来解决实际问题,就能起到事半功倍的效果。本文主要探索PBL教学法在概率论与数理统计课程教学中的应用,通过具体教学案例──条件概率,体现该教学方法的实施过程和效果。
1 PBL教学法的实施过程和教学案例—条件概率
由于条件概率在现实当中有着广泛的应用,可以先给出引例,激发学生学习兴趣,引导学生分析问题和解决问题,进一步引出条件概率的定义。
1.1 问题导入:创设问题情境
例1设有十张奖券,其中三张写着中奖,其余写着谢谢参与。甲乙两人依次来抽奖,问:甲抽完奖券后,乙中奖的概率是多大?
1.2 分析问题
先由学生初步讨论分析:甲先抽奖,由之前所学的等可能概型可知,甲中奖的概率为,因为是依次抽奖,那么会面临这样的问题:甲中奖与否,是否会影响乙中奖的概率?乙中奖的概率又是多大呢?
因为两人是依次抽奖,可以分两种情况来讨论乙中奖的概率:如果甲中奖,则乙中奖的概率为;如果甲未中奖,则乙中奖的概率为。
教师创设情境,为导入新知做准备。由实际问题出发,引导学生思考,建立数学模型,进而用概率论的知识来刻画,并鼓励学生探索数学规律,增加学生学习兴趣。
1.3 条件概率的定义和计算
定义A,B设是两个事件,且P(A)>0称
为在事件A发生的条件下事件B发生的条件概率。
由条件概率的定义可知,条件概率的计算方法有两种:
(1)按条件概率的含义,直接求出P(B|A)。这样方法相当于在缩减了的样本空间S4中计算事件B的概率,如图1所示:
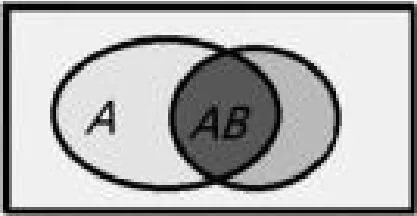
图1 条件概率示意图
例2(续例1)设有十张奖券,其中三张写着中奖,其余写着谢谢参与。甲乙两人依次来抽奖。求已知甲乙两人中恰有一人中奖,中奖人是甲的概率。
分析:这个问题的解决关键是如何正确的建立数学模型,将所求问题转化为随机事件的条件概率。在讲授这个问题的具体解决方法之前,可以让学生分组讨论,先鼓励学生“猜测”所求概率(或者条件概率)可能是多少,再来引导建立数学模型,例如提出问题:怎样才能将这样的实际问题转化为概率的问题呢?以及,如何用条件概率的定义确切地求解和计算该问题?
解:将十张奖券进行标号1,2,…,10,假设1,2,3号奖券上写着中奖,其他号码的奖券上写着谢谢参与。用,表示甲和乙抽到的奖券号码,则样本空间。用表示事件“甲乙两人恰有一人中奖”,表示事件“甲中奖”,则
对于这个问题,可以鼓励学生利用两种条件概率的求解方法,既可以加深对条件概率定义的理解,又可以帮助学生增强建立数学模型的能力。
1.4 条件概率与概率的关系

表1 条件概率与概率的关系
1.5 条件概率的性质
条件概率作为一个集合函数,也有类似于概率的性质,这些性质都可以借助条件概率的定义和概率的性质来证明,不仅能帮助我们计算更复杂的条件概率,还能有助于我们更好的理解条件概率的意义。
例3(续例2)设有十张奖券,其中三张写着中奖,其余写着谢谢参与。甲乙两人依次来抽奖。求已知甲乙两人中恰有一人中奖,中奖人是乙的概率。
分析:这个问题当然可以类似于例2的方法用条件概率的定义求得。但在例2的基础上,也可以用条件概率的性质直接得到。
解:用A表示事件“甲乙两人恰有一人中奖”,B表示事件“甲中奖”,在例2中已经求得,即已知甲乙两人中恰有一人中奖,中奖人是甲的概率为由条件概率的性质可得
即,已知甲乙两人中恰好有一人中奖,是乙中奖(甲未中奖)的概率也为。
在讲解这个例题之前,可以先鼓励学生用条件概率的定义,用类似于例2的方法求解一般,然后教师在启发学生用条件概率的性质直接求解,通过比较两种计算方法,使学生加深对条件概率性质的理解,将这些性质更好地用于实际问题的解决中。
1.6 课后拓展
课后拓展1:随机过程马尔可夫链的转移概率矩阵。
因此,可得矩阵
课后拓展2:条件概率的谬论。
例5有某种重大疾病,可以通过医学检验,来帮助推断个体是否患有该病。但是检验行为也有争议性,因为有检出假阳性结果的可能。设人群中有1%的人患此疾病,医学检验出现假阳性和假阴性的概率都为0.01。人群中随机挑选一人,进行该项医学检验。设表示事件“此人患病”,表示事件“此人检验称阳性”。由假设可知,。假阳性概率,假阴性概率.通过计算可得
从而可知,如果某人真的患病,则检验出现阳性的概率为0.99。但是,已知某人检验出结果呈阳性,此人真的患病的概率仅为0.5。两个条件概率相差很大,而这样的结果对很多人来说也是难以接受的。可见一定要从实际出发,来理解条件概率的真正含义。
2 案例反思及教学效果评价
2.1 案例反思
通过PBL教学方法的实施,学生不仅能够在理论层面上掌握条件概率的定义和性质;而且在能力层面上能够建立数学模型,利用条件概率解决实际问题;进一步的,在思想层面上认识到概率和条件概率辩证关系。在拓展阅读中介绍了条件概率在马尔可夫链的转移概率中的应用,以及介绍了生活中常见的一类关于条件概率的谬论。一方面鼓励学生认真学习条件概率的知识,并给后续其他数学知识的学习做准备,另一方面,也启发学生警惕对数学知识的模糊理解,通过认真分析,保持头脑清醒,就不会被谬论所误导。
2.2 教学效果评价
在概率论与数理统计课程教学中,采用PBL教学法,通过实例吸引学生注意力,以问题为导向,以学生为中心,以分析为重点,以应用来巩固拓展,引导学生思考、解决问题,进而使学生较快理解与掌握概率统计知识的内容及运用。在案例中,通过条件概率谬论,加深对条件概率内容的理解。在课堂教学中要让学生多思、多练、多总结,并安排作业,让学生在巩固课堂学习,课后思考锻炼学生解决实际问题的能力。通过交流互动说明学生已大致掌握条件概率的概念、性质和基本求解步骤,从而说明PBL教学法达到了预期的教学成效。这种教学方法,不仅可以使学生加深了课程知识的理解,更能够提高学生自主学习的兴趣,提高了建立数学模型的技能,增强用数学知识解决实际问题的能力。

