深度体悟，把握数学概念本质

黄肖慧

摘 要：在通过深度学习实现学生高阶思维发展的教育背景下，本文以人教版教材“圆的认识”为例，依托APOS理论的支撑，在学情调查分析的基础上，开展“具身体悟，验证体悟，符号体悟，迁移体悟”四步走的教学实践，引导学生在深度体悟中把握“圆”的概念本质，并进入到方法与策略、经验与联结的思维拓展层面，培养高阶思维.

关键词：体悟；思维；概念本质；圆

近期，笔者有幸加入广东省“南方教研大讲堂”活动的备课团队，参与“圆的认识”一课的备课过程.“圆的认识”是“图形与几何”概念教学的经典课例，是从认识直线图形向认识曲线图形转变的一次飞跃.本课依托杜宾斯基等人的APOS理论，遵循“感知概念—理解概念—描述概念—应用概念”的教学结构，从学生的认知起点出发，以深度体悟引领学生把握“圆”的概念本质，培养高阶思维，打造深度学习课堂.

1 学情分析与课前思考

为把握学生学习的起点，备课团队根据本课的教学目标，以问卷形式对相关知识进行了前测.

通过前测，发现大多数学生知道半径、直径，但能够在圆中准确表示出来的只有10%左右；有超过一半的学生曾经用圆规画过圆，但能准确画指定大小的圆只有极少数.超过70%的学生提出：想研究圆的周长、面积，圆环面积，而“圆的特征”“圆的画法”这些问题被关注度不高.在进一步的访谈中发现，大部分学生未能从数学思考层面来描述圆的本质属性.

“圆的特征”“圆的画法”这些问题，本质上都指向“圆是什么”.通过研究“圆的特征”“圆的画法”可理解“圆是什么”，而理解了“圆是什么”，才能深刻领会“圆的特征”“圆的画法”.因此本课主要分四步走，引领学生深度体悟，发展高阶思维.

2 教学实践

2.1 具身体悟：从操作到想象

圆与其它学习过的平面图形相比，是与众不同的.首先，圆是一个中心对称的曲线图形，圆上任意一点到圆心的距离都相等；其次，半径、直径作为圆的重要组成部分，是隐藏于圆的内部线段.这些都与其它直线平面图形有着本质的区别.^［1］通过分析圆的概念内涵及其在平面图形概念体系中的位置，本课创建“寻宝情境”，来帮助学生获得“平面内与圆心距离相等的动点轨迹”的感性认知，在情境中洞察概念属性.

【片段一】情境中感知圆

师：同学们，根据“宝物在距离小旗2米的草地表面”，你能说出宝物可能藏在哪吗？

小组合作：用一个红点代表小旗，在透明纸上把宝物的可能所在位置用点表示出来.教师展示作品，把各组作品堆叠在一起.

师：当这无数个点汇集在一起，想象一下，连起来会是一个什么图形？你能用手在空中描出这个图形吗？

学生的认知依附于身体，而身体又存在于特定的环境中，创设情境是学生快速进入认知过程的有效途径，它直接影响学习者的投入程度^［2］.动手描点，指尖动作参与概念建构，直观形象地表达动点的抽象轨迹；想象补充，促使动点成圆在头脑中生成；徒手绘圆，及时把头脑中的圆具象化.

2.2 验证体悟：从操作到推理

杜宾斯基的APOS理论认为，第二阶段是概念的过程阶段，是对“活动”进行思考，通过一定的抽象得出概念的特有性质.与引领学生经历“活动”相比，启发学生对“活动”的本身进行思考更为重要.关注获得知识的策略，聚焦数学方法论，才能更深层次地发展学生思维，实现深度理解.

【片段二】验证圆的特征

师：老师提供一些不同大小的圆形纸片，请折一折、画一画、量一量、想一想，探究圆到底有什么特征？

学生合作探究，集中反馈.

师：大小不同的圆，是不是都具备了这些特征？

你是怎么发现这些特征的？

……

师：如果不操作，你能联系情境解释以上特征的合理性吗？

生：宝物距离小旗2米，在以小旗为圆心的2米距离画点，这样的点有无数个，这无数个点与小旗所在位置（圆心）连接，就形成了无数条半径，它们都是2米长……

在探究圆的特征这一活动中，学生表现出不同的思维层次，相当一部分只关注“我发现了什么”这一问题.教师适时追问：“大小不同的圆，是不是都具备了这些特征？”这暗示学生通过找不同大小的圆，举更多的例子来验证.但是，停留在“舉更多的例子”也是不够的，因为例子再多也只是同一思维层面上的单调重复.此时，教师再追问：“你是怎么发现这些特征的？”“如果不操作，你能联系情境解释以上特征的合理性吗？”这是更高层次的引导，从关注“是什么”转向关注“为什么”.思维从动手验证的感性水平上升到推理证明的理性水平.诚然，前者指向知识的陈述，后者指向策略的反思，对学生而言后者是更具成长价值的学习.^［3］

2.3 符号体悟：从操作到抽象

杜宾斯基的APOS理论提出：第三阶段是对象阶段，是对“活动”与“过程”的升华，将抽象出的概念赋予其形式化的定义及符号，成为一个具体的“对象”.

虽然小学教材没有正式提出圆的概念，但是把圆的概念符号化还是必不可少的.进入第三阶段，要把情境中的圆、学具圆片抽象成“对象”，落到纸面上，让学生体悟符号的生成.^［4］

【片段三】对比中画圆

先让学生用圆规在纸上画半径为2厘米的圆.

师：草地上半径2米的大圆，还能用圆规画吗？

师：纸上画圆与草地上画圆，方法有什么不同？

为什么没有圆规也画出了圆呢？

生：确定了圆心和圆心到圆上的距离，就能画出圆.

“两种画圆方法有什么不同？”，这是同中求异，再次引证圆心决定位置，半径决定大小；“为什么没有圆规也画出了圆？”，这是异中求同，引导发现不同工具发挥的相同作用，感受“一中同长”.思考直达概念的核心，逐步实现圆的符号化.

2.4 迁移体悟：从理解到运用

杜宾斯基等人认为，概念学习的第四阶段是运用，是概念进一步的理解、揭示和实例化，最终要形成综合的心理图式.本课的练习环节尝试从概念理解过渡到概念应用，催生联结的思维方式和认知方式.

【片段四】练习中内化圆

练习一：

地震局预测A地于14：23左右将发生6—7级地震，波及范围为20千米.

（地震小常识：地震波在地面的波及范围是一个以震中为圆心的圆）

（1） 在图中画出以A地为震中的危险区域；

（2） 判断B、C两地是否在危险区域内.

练习二：

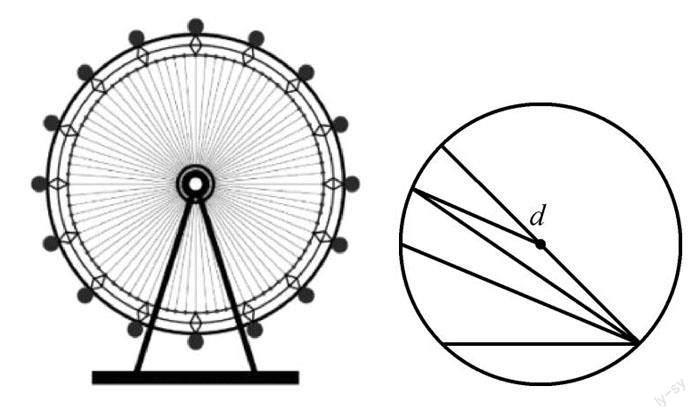
师：公园里有一个摩天轮，如果两个人想坐在摩天轮距离最远的两个座位上，要怎么坐才可以呢？

练习三：拓展研究

寻宝活动中，如果信息改为：“宝物藏在距离小旗2米的地方”，猜想一下，宝物所在位置的轨迹，会是一个什么形状？

练习一创设地震应用情境，进一步揭示圆的本质特征，使圆的应用实例化.练习二创设摩天轮的应用背景，建立圆与其它平面图形之间的知识联结，启发学生对平面图形中线段之间的逻辑关系进行梳理，建立平面图形之间的横向联系.练习三是对概念内涵、外延进行扩大，获得圆与球体概念的逻辑联结，从纵向上初步建立曲线图形概念体系内部之间的联系.

综上，概念学习是不断构建活动、对象、图式的过程.经历感知、内化和概括、复述和反思活动，在深度体悟中把握“圆”的概念本质，并进入到方法与策略、经验与联结的思维拓展层面，方能培养高阶思维.

参考文献：

［1］ 赵元中.用“行”撬动深度的“知”——“圆的认识”教学实践与思考［J］.小学数学教育，2021（10）：70-72.

［2］ 侯凯莹.小学数学具身教学设计研究——以“图形与几何”为例［D］.山西大学，2020.

［3］ 姚进.小学数学中“圆的认识”的教学设计研究——基于APOS理论［D］.扬州大学，2016.

［4］ 陈江辉.关于“圆的认识”教学的再思考［J］.小学数学教师，2018（2）：43-47.