关注学生发展 提升数学素养

黄书东

摘 要：在实际教学中，教师要为学生提供独立思考和合作交流的时间和空间，以此让学生更好地参与课堂，并在参与的过程中深度理解和系统掌握知识，提升学生综合学力.本文以“相交线”为例，通过有效的问题为思维搭建阶梯，让学生在自主探究和合作交流中深刻地理解并掌握了知识，有效地提升了学生的学习品质和学习能力，促进了学生数学核心素养的落实.

关键词：学生；深度理解；数学核心素养

“在传统教学中，数学教学中常常出现”重结果轻过程的现象，尤其在基础知识教学中，教师习惯大包大揽，常常将定义、公式等内容直接呈现给学生，让学生理解并记忆，这样学生对知识的理解是浅层的，不利于知识的系统化建构，不利于学生学习能力的提升.为了改变这一现象，教师应从教学实际出发，为学生搭建一个自主探究的舞台，带领学生经历知识形成和发展的过程，以此让学生获得知识的同时，掌握数学研究方法，提升教学品质^［1］.笔者在教学“相交线”时，为学生精心创设问题情境，让学生在问题的引领下更好地理解知识，促进了数学能力的有效提升.

1 教学简录

1.1 温故知新

师：在小学阶段我们已经学习了平面内两条直线的位置关系，谁来说一说，它们存在怎样的位置关系呢？

生1：相交、垂直、平行.

生2：不对，应该是相交和平行，垂直属于相交.（学生点头表示赞成生2的说法）

师：很好，你能举出一些生活中关于相交的实例吗？

学生积极思考，列举了许多生活中相交线的模型，如钟表指针、纵横交错的道路、剪刀、晾衣架的等等.教师展示晾衣架并点明本课探究的主题——探究“相交线”.

设计意图：借助旧知和生活实例引出本课的主题，以此拉近学生与数学的距离，激发学生学习的热情，为接下来自主探究和合作交流创造条件.

1.2 探究新知

探究1 相交线的性质

环节1：互动交流，抽象概念

师：请同学们自己画一组相交线，并仔细观察，看看从这组相交线中是否能够找到熟悉的几何图形呢？

学生画图并观察，很快就有了发现.

生3：图形中有角.

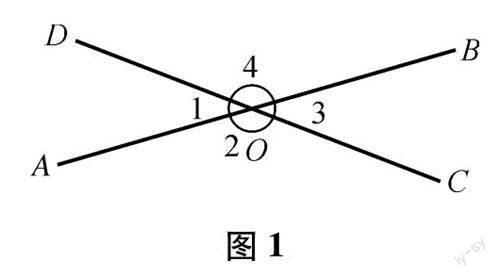
师：观察得非常仔细，现在我们把这些角标注一下.（教师在黑板上画出相交线，并进行了标记，如图1所示）

师：两条相交的直线构成4个角，记作∠1，∠2，∠3，∠4.观察一下，这四个角存在怎样的位置关系？（教师鼓励学生观察并交流）

生4：∠1和∠4，∠1和∠2的位置相邻；∠1和∠3，∠2和∠4的位置相对.

师：说得非常好，还有其他补充吗？

生5：相邻的还有∠3和∠4，∠3和∠2.

师：同学们说得非常好，这样我们就将四个角分成了两类，即相邻和相对.仔细观察∠1和∠3，你能用数学语言描述一下你理解的“相对”吗？（学生积极思考）

生6：它们有公共的顶点，且两条边在同一直线上.

生7：两条边互为反向延长线.

由此通过观察、交流，教师给出对顶角的概念也就水到渠成了.在教学中，教师引导学生经历概念的形成过程，有利于培养了学生数学抽象概括能力，有利于提升数学素养.

环节2：互动练习促深化

为了让学生进一步理解概念，发现对顶角的性质，教师设计了如下练习：

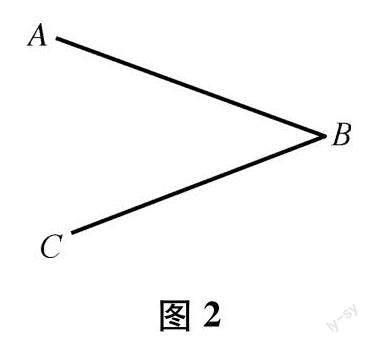
练习1：如图2，你能画出∠ABC的对顶角吗？

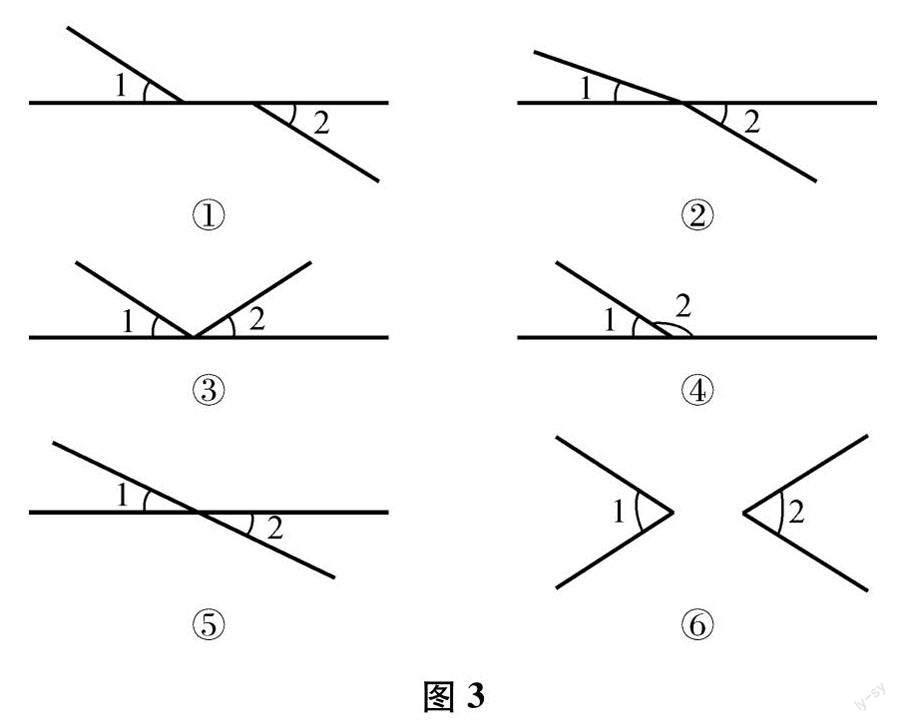
练习2：如图3，∠1和∠2是否为对顶角呢？（教师PPT给出图形让学生辨析）

对于练习1，教师点名让学生上台画，并口述对顶角的定义.对于练习2，学生给出正确答案后，教师让学生给出不是对顶角的理由，以此通过说一说、画一画，促进对概念认识的深化.

环节3：合作探究，生成性质

师：刚刚从位置关系的角度出发明确了对顶角的概念.从数量关系的角度去分析，它们又会存在怎样的关系呢？（教师给出图1让学生观察）

生8：∠1和∠3相等.

师：你是如何判断的.

生8：我用眼睛看的.

师：你能利用所学的知识验证这一数量关系吗？

生8：可以用测量法.

师：是一个不错的方法，还有其他方法吗？

生9：可以运用叠合法.

师：也是一个不错的想法.不过利用这两种方法是否真的可以验证∠1=∠3呢？

生10：不能，这两种方法都是存在誤差的.

师：确实，那么是不是我们就无法验证它们相等了呢？思考一下，我们之前学习的平角知识，看看你有什么发现？（教师进行启发、引导）

生11：∠1+∠2=180°，∠2+∠3=180°，（∠1+∠2）-（∠2+∠3）=0°，∠1-∠3=0°，所以∠1=∠3.

教师对生11的证明方法给予肯定，并通过师生互动交流对以上证明过程进行简化：因为∠1+∠2=180°，∠2+∠3=180°，所以∠1=∠3.这样通过互动交流学生发现了“对等角相等”这一重要性质，体验了几何证明的魅力.为了让学生理解、运用对等角的性质，教师又设计了相应的练习，进而通过具体应用促进知识的内化.

探究2 两直线垂直

环节1：巧用分类，引出垂直

师：思考一下，两条相交直线所构成的角可以如何分类呢？

生12：锐角、钝角.（学生不假思索地说）

师：还有其它角吗？

生13：应该还有直角.

师：补充得非常好，两直线相交可以形成三种角：锐角、钝角、直角.

师：若两条直线相交所形成的角中，其中一个为直角，那么其它三个角是什么角呢？

生14：都是直角.如图1，假定∠1为直角，∠3是其对顶角，故∠1=∠3，所以∠3也是直角.而∠1+∠2=180°，∠1+∠4=180°，所以∠1和∠2都是直角.（学生掌声）

师：很好，对于两条相交线，若有一个角是直角，就称这两条直线垂直.

在此基础上，教师给出了两条直线互相垂直的定义，表示方法等.

环节2：巧借情境，促进深化

师：在生活中有哪些垂直的例子呢？已知一条直线，你能画出它的垂线吗？

教师鼓励学生思考、表達、操作，进一步理解两直线互相垂直的定义.

以上教学活动中，教师为学生创设了具有明确指向性的问题情境，让学生通过自主探究和合作交流总结归纳出了相关的定义、性质，充分体验了数学探究的乐趣.

1.3 课堂小结

师：在探究“对等角相等”这一性质时，我们经历了哪些过程？通过本课的学习，你有哪些收获？你认为接下来可以研究什么内容呢？

在该环节教师先是让学生自己回顾、反思、总结，然后进行小组交流，并预留充足的时间进行课堂互动，以此让学生通过有效的回顾、反思、交流进一步理解相关的定义、性质，同时让学生明白研究几何图形就是研究其构成图形的关系，以此让学生认清研究几何图形的本质，为接下来探究平面几何图形问题提供思想保障.另外，通过总结归纳让学生明白，数学结论的得出一般需要经历观察、猜想、验证、说理等过程，以此让学生感受数学的严密性，为接下来的几何证明的研究提供依据.

1.4 课后作业

在课堂教学中，教师已经设计了相应的练习，了解了学生的基础知识的实际掌握情况.为此，在课后练习中，教师应该侧重于学生之所惑，通过有针对性地练习帮助学生消除困惑，强化知识，提高作业有效性.

2 教学思考

以上教学设计贯彻了“以生为主”的教育理念，关注学生探究能力的提升和数学核心素养的落实.在整个教学过程中，教师精心设计问题，让学生的思维在问题的驱动下变得更加“有序”，加速了新知的生成，提高了教学有效性.

2.1 有利于基础知识的深度理解

理解并掌握知识是应用知识的前提，是培养学生数学素养的基础.在教学中，教师要从学生实际出发，合理整合教学资源，关注对基础知识学习的整体建构，让学生能够站在更高的角度审视数学学习，促进知识的深度理解^［2］.在探究相交线的性质的过程中，教师从学生的已有经验出发，让学生通过经历操作、观察、猜想、验证等过程抽象出了相关的定义、性质，让学生领悟了探究几何图形性质的一般方法，提升了学生数学探究能力，提升了学生数学素养.

2.2 有利于学生自主学习能力的提升

让学生学会学习是数学教学的重要使命，是培养学生数学核心素养的关键^［3］.在课例教学中，教师提出问题后预留时间让学生独立思考，主动表达，为学生自主学习能力的培养提供了发展的契机.

2.3 有利于合作探究能力的提升

在本课教学中，教师设计了多个问题.学生在问题的驱动下积极互动，在获得知识的同时锻炼了数学语言表达能力，培养了学生合作探究能力.以上教学活动以学生探究为主线，充分地调动了学生参与的积极性，锻炼了学生的思维能力，有利于学生数学核心素养的落实.

总之，在教学中，教师要站在知识系统的角度设计问题，让学生在解决问题的过程中不仅可以收获知识，而且能够掌握数学研究的方法，以此提升学生品质，提高教学有效性.

参考文献：

［1］ 徐宣林.初中数学课堂教学中学生自主学习能力的培养探究［J］.好日子，2021（24）：291.

［2］ 丁晓玲.巧引数学反思，促进思维生长［J］.数学大世界：上旬，2021（10）：39-40.

［3］ 褚蒙蒙.打造生长课堂 促进主动建构［J］.数学大世界：中旬，2021（10）：7-8.