品味提问艺术,优化解题教学
苏州高新区第一初级中学校 王 珍
有效教学是当前教育教学领域中最为热门的话题之一,更是一线数学教师十分关注的目标.众所周知,教师若不谙熟提问的艺术,其教学就谈不上有效,课堂教学的成功很大程度上取决于教师的巧妙提问及智慧点拨.由此可见,艺术性的提问对构建有效教学的作用不可低估.笔者在多年的教学实践中十分注重提问的艺术性,也积累和总结出一定的经验,下面就解题教学这一视角具体阐述.
1 凸显层次性
在教学的过程中,我们偶尔会面临这样的情形:一个问题提出后,学生个个面面相觑,呈现无人应答的“冷场”局面.面对这样的情形,一些教学经验尚浅的教师则会埋怨学生不够灵活,思维能力薄弱.事实上,造成这种“冷场”现象有时是因为教师设计的问题门槛过高.此时,需要教师针对问题的特征,设计一连串阶梯性提问,层层递进地引领学生的思维不断延伸,循循善诱,助力学生更好地解决问题,提高学生的解题能力.
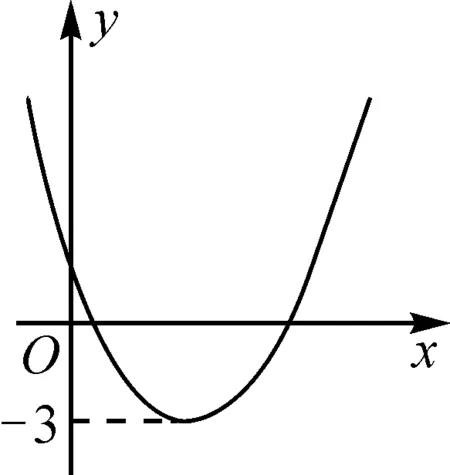
图1
案例1图1为二次函数y=ax2+bx+c(a≠0)的图象,若关于x的方程|ax2+bx+c|=k(k≠0)有两个不等实根,试求k的取值范围.
由于学生初学二次函数,因而对此问题感觉到生疏且有难度.为了更好地促进学生理解,笔者精心设计如下问题串进行点拨:
问题1说一说y=ax2+bx+c的图象是什么?
问题2y=|ax2+bx+c|的图象呢?你能画一画吗?
问题3那y=k的图象呢?也请画一画.
问题4方程|ax2+bx+c|=k有两个不等实根用图象表示的意义是什么?
解题是检验学生知识掌握情况的有效标准.以上案例中,教师问题的抛出并非随性而为,而是经过对具体学情的了解而精心设计的.正是由于有了各种思虑,教师才能针对原题巧妙点拨与诱导.这样,通过一组拾阶而上的问题引领学生思维不断攀爬,逐步攀上一个崭新的高度,从而使复杂问题迎刃而解,让学生品尝到解题成功的愉悦感,同时提高学生发现与挖掘的意识,让学生掌握创新解题的一般方法[1].
2 体现探究性
初中数学教学效率低的症结到底何在?笔者认为,从根本上来说就是不善变通的解题策略和铺天盖地的题海战术.创新是民族进步的灵魂.因此,教师在设计数学问题时,需基于学生的“最近发展区”精心设计能体现探究性的数学问题,利用富有探究价值的习题促使学生都能竭尽所能地“跳一跳”,试着“摘桃子”.这样深入探索的过程,不仅满足了学生的求知欲望,还能给予学生解题的信心,这样的问题才能达到“以一敌百”的效果.反之,教师若仅仅以解题的数量来论长短,教学效率低下的现状根本无法得到改善,还会导致学生学习兴趣的丧失,提高创新能力更是无从谈起.这里需要重点关注的是,过难的问题会打消学生的积极性,过易的问题会影响学生的探索热情,这就需要教师深钻教材、了解学生,巧妙设计,方能提高学生的解题能力.
案例2以完全平方公式的拓展运用为例
此时的学生可以熟练运用公式进行多项式的运算,为了给学生提供更多的应用体验来深化学生的认知,提升学生思维的灵活性,笔者精心设计了以下问题串:
问题1已知a+b=3,ab=2,求a2+b2,a-b.
问题2已知ab=3,试求a2+b2的最小值.

以上案例中,教师的问题设计是对教学内容的深度挖掘,关注到了问题的自然性,而并非人为创造的一些难题.通过这样具有探究性的问题串,让学生深刻明晰完全平方公式对于多项式运算的各种简便,让学生在灵活运用中学会思维、学会多角度去理解,更重要的是这里的活用也为后续“求代数式的最值”提供了方法上的借鉴.如此问题引领,让整个课堂变得完美,让学生真正进入思考与探索的境地,培养了学生的探究精神,真可谓效能丰富.
3 注重针对性
对于数学解题而言,教师设计的问题不仅需具有探究性,还需具有一定的针对性,才能让学生在数学探究的过程中深入思考,多层次、多角度地探究,从而充分发挥问题的价值,让学生通过解决问题全面而深刻地掌握知识,收获真理,培养他们的创造性思维[2].
案例3以“四边形问题中的折叠类问题”为例
问题1请试着通过折叠探寻矩形纸片的对称中心,并找寻它的对称轴.
问题2请利用剪刀剪一次,将矩形纸片分成面积相等的两个部分.你能找到多少种不同的剪法?
问题3请从理论角度证明“过矩形对称中心的直线平分矩形的面积”.
问题4上述理论除了以上角度,是否还能从图形变化的角度予以证明?
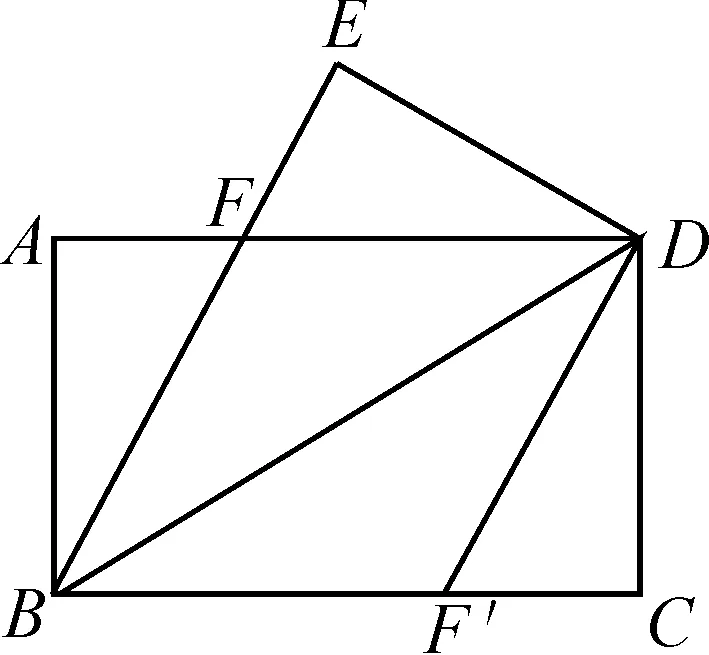
图2
问题5如图2,将矩形ABCD纸片沿着对角线BD折叠,将不重叠的部分剪掉,再展开重叠部分,将不重叠的两个部分,即△ABF与△EDF拼成一个图形,作图并说一说拼出的图形名称.
问题6请试着从图形变换的角度说明这些图形是如何变换得到的.
问题7请试着将这些图形进行分类.
问题8上述活动中,用到了什么数学思想方法?
问题9请试着用折纸法验证“直角三角形斜边上的中线等于斜边的一半”.
问题10沿着BD剪开刚才的重合部分,得出△BDF.你是否能将这张纸片折叠成一个矩形?
不少教师在提问时只是微观地考虑问题是否具有探究性,却往往忽视了从宏观上对知识本质的考量.以上案例中,教师设计的每一个问题都是经过了深思熟虑的.通过问题的解决不仅让每个学生都能深化对四边形的认识,而且培养了学生的创造性思维,建构了高效数学课堂,提高了学生的数学素养[3].
4 彰显主体性
教学活动是一种双边活动,其中教师起到了主导作用,而作为教育客体的学生,也是教学的主体.如何在教学的过程中彰显其主体地位呢?笔者认为,学生的主体性主要体现在积极动口、动手和动脑,在以动脑为核心的多感官参与下习得知识、生长能力、发展思维.课堂中可以引发学生多感官参与的一定是教师提出的体现教师创造性劳动成果的数学问题.因此,教师需设计彰显主体性的数学问题,引起学生积极主动地思考,促使其在思考中辨析、在辨析中生成,让学生的思维得到锻炼与发展.

图3
案例4如图3,已知△ABC内接于⊙O,AD为⊙O的一条直径,且与边BC相交于点E.若OE=3,DE=2,试求tanC·tanB的值.
本题具有一定的难度.为了不造成学生无从下手的局面,笔者设计了以下问题串:
问题1试求BE∶CE的值.
问题2看到直径,通常都会怎么作辅助线?
问题3tanB与tanC该如何转化?
问题4你觉得tanC·tanB可以转化为什么?
课堂中,有了教师的提问,才有了学生的深度思考;有了教师的提问,才有了学生的积极探索.以上案例中,教师以问题串为载体进行启发与诱导,给予学生极大的思维支撑.更重要的是,在问题抛出后,教师充分留白,让学生进行充分的思考、充分的讨论和充分的表达,从而让问题的解决水到渠成.如此提问,不仅彰显了主体性,同时也较好地达成了教学目标,从而培养了学生的核心素养.
总之,在学生学习的道路上,教师充当的是引路人的角色,因此,教师需要深度钻研、思考与反思提问的技巧与策略,让学生通过精心设计的问题得到更好的训练与展示,以达到优化教学的效果.对于解题教学而言,面对不同题目,教师需要针对具体的学情,针对性地精心设计,这样才能发挥提问的作用,优化解题教学,培养学生的思维能力.

