一种基于视觉测量的SCARA机器人标定方法

王文双，姚书杰，曾 钰，谢启旋

（1.广州智能装备研究院有限公司，广州 510530；2.华南农业大学工程学院，广州 510642）

0 引言

SCARA 机器人在生产过程中，不可避免地存在机械加工误差。此外，在装配、维修和长时间使用后，SCARA 机器人还会产生杆件变形、磨损、间隙等问题。这些问题都会导致SCARA 机器人的参数发生变化，影响SCARA 机器人的精度，使SCARA 机器人无法完成精准的操作任务。为了提升末端执行器位姿的控制精度，使SCARA 机器人能够正常工作，不得不重新进行标定，确定SCARA 机器人的零点位置和大小臂的实际长度。

何沁珊等[1]采用定位销的方式将大小臂固定理想位置来完成零点标定，该方式操作简单方便，但精度不高。许允斗等[2]做了2RPU/UPR+RP 过约束混联机器人零点标定和全标定理论研究，有效提高混联机器人的定位精度，但必须借助激光跟踪仪这种高精度的测量设备。梅江平[3]等提出了一种基于末端转角误差信息的快速零点标定方法，该零点标定方法的鲁棒性好，准确性高，但该方法只适用于并联机器人。潘伯钊等[4]采用激光三坐标测量装置对机器人进行标定，该方法得到的精度较高，但设备价格昂贵。郎需林等[5]通过多点法计算零点的位置，但计算过程复杂，实现起来比较困难。

SCARA 机器人的零点标定已经存在比较成熟的技术和研究，但是大多数的标定方法都需要借助一些昂贵的仪器，且操作过程十分复杂和繁琐，需要专业的人员才能完成工作，使用起来十分不方便。本文在前人研究的基础上，提出了一种简单，实用的SCARA 机器人零点标定方法，用于解决SCARA 机器人标定过程中存在的问题。该标定方法具有操作简单、设备便宜、精度高的优点，能满足绝大部分情况下SCARA 机器人的工作要求。

1 算法原理

1.1 SCARA机器人运动学正解

如图1 所示，在基坐标原点O处建立机器人的基坐标系xoy，OA为机器人的大臂，长度为L1，OB为机器人的小臂，长度为L2。点O和A在机器人的关节处，B与机器人的末端重合。末端处点B的x轴坐标值为向量OA与向量AB在x轴上的投影之和，y轴坐标值为向量OA与向量AB在x轴上的投影之和，故有：

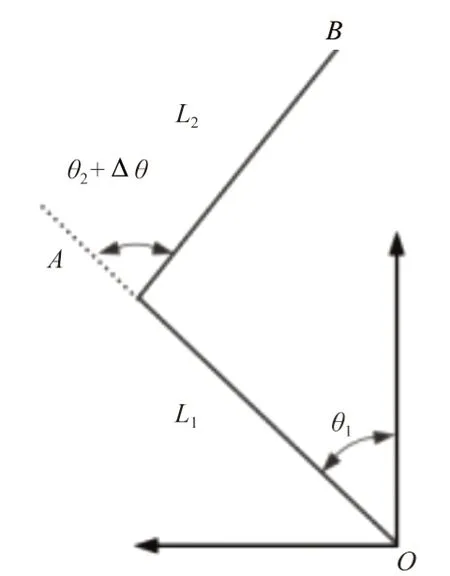
图1 运动学正解图

式中：θ1为x轴与OA的夹角；θ2为OA与AB的夹角；Δθ2为机器人大臂与小臂的理论值与实际值的角度偏差。

1.2 SCARA机器人运动学反解

如图2 所示，建立机器人的基坐标系xoy，连接OB，过点B做OA的垂线BC，交OA于点C。在直角三角形OBC中，根据余弦定理，可得：

图2 运动学反解图

机器人处于右手系时，S2取正值；机器人处于左手系，S2取负值，特别的，机器人处于奇异位置时，则S2=0。

根据式（3），可求得θ2：

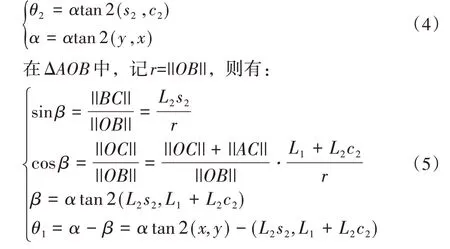
scara机器人的运动学反解[4]为：

爱璞特（AP&T）是一家瑞典公司，在瑞典拥有两家制造工厂，在意大利拥有一家制造工厂。产品通过位于丹麦、德国、波兰、中国、瑞典、日本和美国的销售及维修公司以及在其他市场设立的代理机构销往世界各地。整个集团拥有将近400名员工，针对成形金属零件的制造商，开发、生产并销售完善的生产系统、自动化设备、压力机和模具，并提供相关的售后服务。

本文约定，当θ2∈（0，π）⋃（-2π，-π）时机器人处于右手系；当θ2∈（-π，0）⋃（π，2π）时，机器人处于左手系。特别地，当θ2∈{-2π，-π，0，π，2π}，机器人处于奇异位置。

1.3 误差分析

机器人误差的主要来源为几何误差，即在机器人的制造与装配过程中，由于装配体本身存在间隙误差，装配精度低，机械加工误差，或长时间使用导致的零件磨损等因素，致使SCARA 机器人的大臂关节轴线的位置和小臂关节轴线之间的相对位姿关系产生误差。一般通过提高加工与装配的精度来尽量避免这样的几何误差，但是由于数控加工机床本身加工精度以及不可避免的人工操作误差，这种方法显然不能完全避免这样的误差。所以，需要通过零点标定的方法来提高SCARA 机器人的精度，即首先找出关键的几何误差参数，然后通过运动学标定方法求出参数实际值。

SCARA 机器人共有4 个轴和4 个运动自由度，其中有3 个旋转关节，其轴线相互平行，在平面内进行定位和定向。另一个关节是移动关节，用于完成末端件在垂直于平面的运动，即包括绕X、Y、Z轴的旋转和沿Z轴的平移自由度。其中大臂与基底的装配和磨损导致两臂轴线不完全重合所造成的误差，可由大臂长度进行补偿，垂直移动关节与小臂轴线不完全重合所造成的误差对零点位置的影响较小，可以忽略不计。其他的误差则由前面所得公式求出。

根据前文所求出的SCARA 机器人正解公式（1）和反解公式（6），可知机器人的几何误差主要包括大臂长度L1的误差，小臂长度L2的误差和大小臂之间实际值与理论值的角度偏差Δθ2。

1.4 零点和臂长的标定步骤及原理

如图3 所示，建立SCARA 机器人的基坐标系xoy，其中，点O与机器人的基坐标系的原点重合。M、N为标定器上的两个辅助点，他们分别为图4 中标定器上的圆形和十字形的中点。A1（1）、A1（2）为相机图像中点与点M从两个不同方向完全重合时，机器人大臂和小臂的交点。

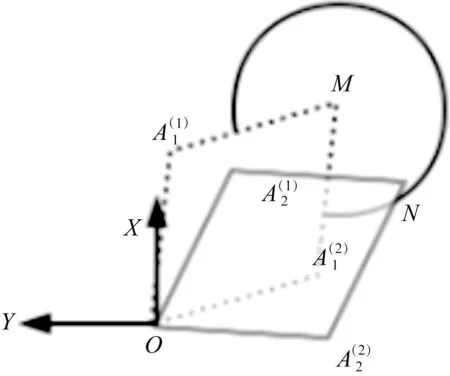
图3 标定图

标定步骤如下。

1.5 误差估算

圆柱形标定器的示意图如图4 所示，其半径的大小为R，点M为标定器上圆形模板的中点，点N为十字形模板的中点。

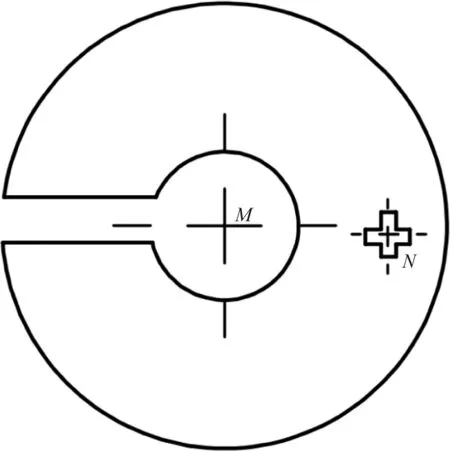
图4 标定器

误差测量步骤如下。

（1）将相机摆放到机器人活动范围内下方的任意位置。

（2）调整相机方向，使相机成像平面与标定器底面平行。

（3）调整相机位置，使点M与成像平面的中心点（U，V）重合。

（4）以r为半径，机器人带动标定器绕成像平面的中心点画圆，并记录下n个点在图像坐标系下的坐标（ui，vi）和在基坐标系下的坐标（xi，yi）。

（5）在另一个手系下，根据矫正后的角度和运动学反解，机器人运动到（xi，yi），记录下对应n个点在图像坐标系下的坐标（ui′，vi′）。

根据上述步骤中，可得机器人的位置像素误差平均值为：

2 实例验证

本文采用SCARA 机器人进行实验。图5 所示为SCARA 机器人和实验平台，图6 所示为装在机器人末端的标定器。实验所用机器人的大臂设计长度值为350 mm，小臂设计长度值为250 mm。所用相机为迈德威视的工业相机，分辨率为2 448×2 048。实验过程中，让相机镜头向上，与机器人移动轴上的标定器平行，成像平面的中心点与第四轴的中心在一条直线上。相机的固定台保持不动，以此保证相机不会发生空间位移。通过调整光源增加相机的亮度，来提高标定器上两个图形与背景的对比度。

图5 标定工作平台

图6 标定器实物

实验利用德国MVtec 公司开发的HALCON 机器视觉算法包进行二次开发，根据HALCON 中的模板匹配算法开发出一个识别软件，来识别图中标定器的圆形中点和十字形中点，用以作为辅助零点标定的特征点。识别前，需要准备从标定器原图上截下来的两种特征图形的图片，或从原图中将两种特征框选出来。识别过程中，将固定在机器人垂直移动轴上的标定器移动到图像中，即可将特征框选出来，并标记其中心点作为辅助标定的特征点。移动SCARA 机器人，使标定器发生旋转时，HALCON 机器视觉算法包的模板匹配算法也能精确识别出标示形状及其中心点，完成辅助标定的任务。

根据前文所述的零点和臂长标定步骤以及误差估算方法，对SCARA机器人进行标定。测试结果如表1所示。

表1 标定实验数据及计算结果

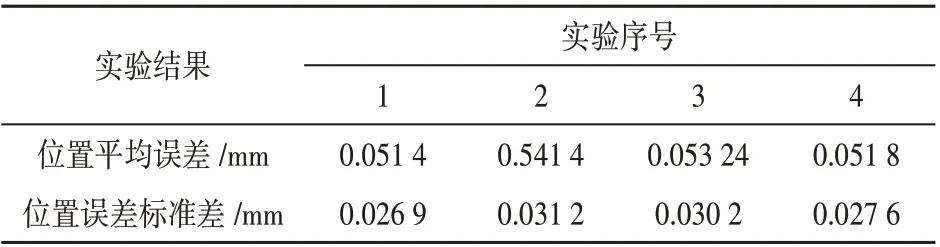
表2 标定误差测定结果

3 结束语

本文针对SCARA 机器人的精度问题，以SCARA 机器人的零点标定方法为研究对象，根据机器人的正反解公式，分析了其误差源参数，建立其零点标定的方程，以此对SCARA 机器人进行了零点标定。提出了零点标定的视觉测量原理，搭建了标定实验平台，得到了实验所用机器人的大臂长度误差参数，小臂长度误差参数，以及它们之间的角度误差参数的真实值，并计算了SCARA机器人的定位精度误差。

从实验结果来看，经过零点标定之后，所用SCARA机器人的位置误差控制在了0.06 mm 以内，大臂的长度误差在0.03 mm 以内，小臂的长度误差在0.025 mm 以内，标定精度较高，达到了一般情况下SCARA 机器人的工作要求。

综上所述，相对于传统的标定方法需要昂贵的测量设备，且标定过程复杂，本文所提出的方法具有测量仪器简单、操作流程简易、适用范围广等优点，便于在工业上的应用。