基于奇异避免的薄壁件镜像铣削加工路径优化

钱 栊 张立强 高秋阁 杨 杰

上海工程技术大学机械与汽车工程学院，上海，201620

0 引言

在航空制造领域，蒙皮作为重要的飞机外表零件被广泛使用[1]。飞机蒙皮零件具有尺寸大、厚度小、外形复杂等特点，在加工过程中易发生振颤，检测难度大[2-3]。传统的飞机蒙皮加工方式采用化学铣削加工[4]，化学铣削在工艺和设备的使用上都较为便捷，并且操作方便、投资少。化学铣削加工时至今日在制造业领域仍然起着不可忽视的作用。随着数字控制技术的发展，以及加快构建绿色制造体系、大力发展绿色制造产业的提出，蒙皮零件的加工朝着低碳、低成本、绿色的新型能耗标准转型，镜像铣削加工是一种针对大型薄壁件开发的新型加工技术，其优越性也已经得到验证[5]。镜像铣削加工系统由两端对称的卧式五轴机床组成，一侧是五轴铣头，另一侧是对称的五轴支撑系统。在加工过程中，铣头与支撑头轴线时刻保持在同一条直线上，并且与蒙皮表面垂直，保证蒙皮加工区域的局部刚性。同时，支撑头还带有激光扫描、实时测厚补偿等功能，镜像铣削加工技术能够显著提高蒙皮的生产效率和加工质量，是目前蒙皮数字化制造的关键和发展趋势。

五轴机床的运动轴会由于运动突变而引起奇异问题，这在镜像铣削加工过程中也不可避免地会遇到[6]。奇异问题会引起加工轨迹不光顺，当进入奇异区域时，机床旋转轴运动剧烈，无法满足其动态性能，进而影响机床的加工精度，导致加工效率的降低，加工零件的表面质量达不到要求。

针对五轴的奇异问题，国内外已进行了大量的研究。YANG等[7]通过优化刀轴矢量对样条曲线控制点进行微调，从而规避奇异区域；MUNLIN等[8]对A、C轴的旋转角度进行最优值选择，减小了旋转角的急剧变化，但是在调整旋转轴时会引入加工误差；KNUT[9]通过在奇异点附近插入刀位点来减小经过奇异点的加工误差；王峰等[10]提出对奇异区域检测的条件，由于缺少关于“病态”条件数的定量标准，因此无法精确计算且效率较低；郑飂默等[11]使用实时插补方法在刀位点处进行平滑连接，加工质量得到了提高；王丹等[12]对奇异区域的刀位点进行线性插值，提高了加工件的精度。针对五轴的奇异问题，上述研究主要通过优化刀轴矢量来实现加工路径的光顺。但对于镜像铣削而言，铣头与支撑头必须垂直于工件表面的同时，还需要保证支撑侧壁厚测量的稳定和准确，所以仅仅是修改刀轴矢量会导致法向的偏离，影响加工表面质量和精度要求。

本文针对镜像铣削过程中旋转轴运动突变带来的奇异问题，基于C-空间的概念，在奇异区域边界约束条件下，同时满足镜像铣削加工中刀轴矢量与工件表面保持垂直，以最小刀轴矢量距离确定备选刀轴矢量，对奇异区域的刀轴矢量进行局部修正。然后对整条加工路径进行B样条曲线拟合，基于最小参数曲线应变能建立优化模型，通过对参数曲线的调整，提高优化路径的光顺性，保证加工效率，提高加工质量。最后，通过仿真实验和实际加工结果验证了本文方法可有效解决薄壁件镜像铣削加工过程中的奇异问题。

1 双五轴机床运动学变换与奇异问题分析

1.1 C1-A1、B2-A2双五轴卧式机床旋转轴运动学变换

本文以C1-A1、B2-A2双五轴镜像铣机床为研究对象，如图1所示。铣削侧为C1-A1双摆头结构，其旋转轴的旋转量分别记为A1和C1。铣削侧的刀轴矢量表达式为

(1)

图1 双五轴镜像铣机床Fig.1 Double five-axis mirror milling machine

根据式(1)可以通过铣削侧运动学逆变换求得A1和C1角的解为

(2)

其中,A1角的取值范围为[-90°，90°]，C1角的取值范围为[-360°，360°]，kA1、kC1分别为求解旋转轴A1和C1的解系数，kA1=±1,kC1=0或kC1=±2。k决定了A1轴的变化量，i和j决定了C1轴的变化量。C1角与i和j的取值关系如表1所示。

表1 C1角与i、j的取值关系

支撑装置为B2-A2双摆头结构，其旋转轴的旋转量分别记为A2和B2。支撑头运动的刀轴矢量表达式为

(3)

根据支撑侧旋转轴运动学逆变换分析，旋转角存在多解。当j=±1时，所求得A2和B2角的解为

(4)

当j≠±1时，所求得A2和B2角的解为

(5)

其中，A2的取值范围为[-65°，65°]，B2的取值范围为[-360°，360°]，kB2为求解旋转轴B2的解系数，kB2=0或kB2=±2。

1.2 旋转轴奇异问题分析

镜像铣削机床在加工过程中集随动支撑、壁厚在线测量、加工误差补偿等功能于一体。镜像铣削加工系统由两端对称的卧式五轴机床组成，一侧是五轴铣头，另一侧是对称的五轴支撑系统。本文针对镜像铣削加工中遇到的奇异问题，已在1.1节中对镜像铣削两侧的五轴运动学变换进行了运动描述。

针对支撑侧B2-A2双摆头结构，A2角为±90°时，此时i=0,k=0,由式(3)可知，此时刀轴矢量(i,j,k)T=(0,1,0)T,且为支撑侧的奇异点。由于支撑侧A2角的取值范围为[-65°，65°]，不会到达±90°的位置，因此在镜像铣削加工中，可以不用考虑支撑侧旋转轴的奇异问题。

针对铣削侧C1-A1双摆头结构，当A1角为0°时，机床会失去一个旋转轴的运动能力，即C1轴的旋转量无论取何值，都不会改变刀轴方向。由式(1)可知，此时刀轴矢量(i,j,k)T=(0，0，1)T，由表1可知，C1角的解在i=0且j=0时无法确定，(0，0，1)T为铣削侧奇异点的位置。根据文献[13]方法，可以得到奇异区域边界大小为βmin，即A1≤βmin的范围为铣削侧加工刀路的奇异区域，图2所示的圆锥区域称之为奇异区域。

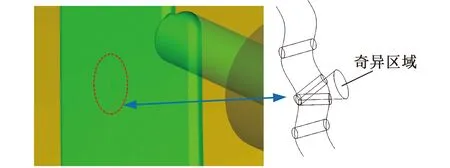
图2 奇异区域示意图Fig.2 Diagram of singular region

2 双五轴铣削侧加工奇异区域刀具路径优化

2.1 基于C-空间的刀轴矢量选择

对于产生了奇异问题的刀轴矢量，可采用C-空间的概念[14-16]对无干涉区域以及奇异域作进一步处理。无干涉区域的确定可采用C-空间的形式，将旋转轴的运动作为参数空间的两个方向，将障碍物变换至C-空间内，然后去除代表障碍物的C-空间点，即可得到无干涉可行域，同样地，为得到无奇异的可行域，可将奇异域视为障碍物体映射至C-空间内，并作为要去除的点进一步处理，即对产生奇异问题的刀轴矢量选择新的刀轴矢量进行替代。具体来说，无干涉区域和奇异域基于C-空间的形式将刀轴矢量作表达处理并重新选择无干涉无奇异区域的刀轴矢量进行替代，当刀位点Pi(xi,yi,zi,ii,ji,k)落在A1≤βmin的奇异区域内，也就是刀位点的刀轴矢量V=(i,j,k)T落在SB-SA区域的外侧，如图3所示，其中SB为无干涉区域(即红色椭圆区域)，SA为奇异区域(即蓝色椭圆区域)，SB-SA为无干涉无奇异区域(即红色椭圆区域去除重叠部分)。

图3 无干涉无奇异可行域Fig.3 Feasible area with no interference andno singularity

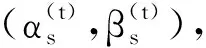
(6)

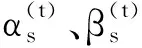
2.2 基于奇异域内刀轴矢量边界约束条件

在双五轴镜像铣削加工过程中，工艺编制前置处理所得到的刀位文件如图4所示。其中(x,y,z)T为刀尖点的位置，(i,j,k)T为刀位点处的刀轴矢量，将奇异区域的起始刀位点设为Pm(x1,y1,z1,i1,j1,k1)、终止刀位点设为Pn(x2,y2,z2,i2,j2,k2)，识别出的刀位点数量为N，奇异区域内加工时间为Ts，则奇异区域内刀位点各个坐标方向的切矢可通过下式计算：

(7)

图4 前置刀位文件Fig.4 Front tool path file

式中，km、kn分别为奇异区域起始位置的切矢和终止位置的切矢；Pm-1、Pn-1分别为奇异区域起始刀位点的前一刀位点和终止刀位点的前一刀位点。

此外，在镜像铣削加工过程中，铣削侧的刀具与支撑头同步运动，且在支撑侧安装的超声波测厚传感器在机床加工过程中实时测量工件的壁厚，以实现加工过程中的稳定性，因此为了保证工件壁厚测量的准确性，加工过程中的刀路刀轴矢量需时刻与工件表面保持垂直，所以同步运动的刀轴轴线与蒙皮工件表面的法向保持相同，即

V=nR

(8)

式中，nR为蒙皮工件表面R加工过程中该刀位点处的法向矢量。

2.3 奇异区域刀路优化方法

针对奇异问题的解决办法一般有插值法和刀路避让法，插值法可以减小旋转轴运动过程中的角度，但这并不能完全避开奇异区域；刀路避让法可以避开奇异区域，但是修改的刀位点所产生的误差无法满足正常刀位点误差范围的要求，尤其是对于双五轴镜像铣削而言，加工过程中的刀轴矢量需要时刻与被加工工件表面保持垂直，从而保证镜像铣削加工效率和表面质量。

本文所提方法的流程如图5所示，即所采用的刀路调整策略是将刀轴矢量拟合成B样条曲线，通过最小误差曲线应变能ΔEmin来保证参数曲线拟合的连续性和光顺性，且在刀轴矢量拟合过程中还得满足刀轴矢量基于C-空间的选择，并将km、kn作为边界约束条件，将刀轴矢量进行B样条曲线的拟合，以参数曲线的应变能最小化为目标，得到B样条曲线的控制系数从而实现奇异区域的刀路优化，具体步骤如下：

(1)在蒙皮工件表面构造初始刀路，读取前置刀位文件，得到刀位点数据Pi(xi,yi,zi,ii,ji,ki)，刀位点数据可通过Catia中设计的刀具路径来获得，经过线编程功能和导出功能获取前置刀位文件。

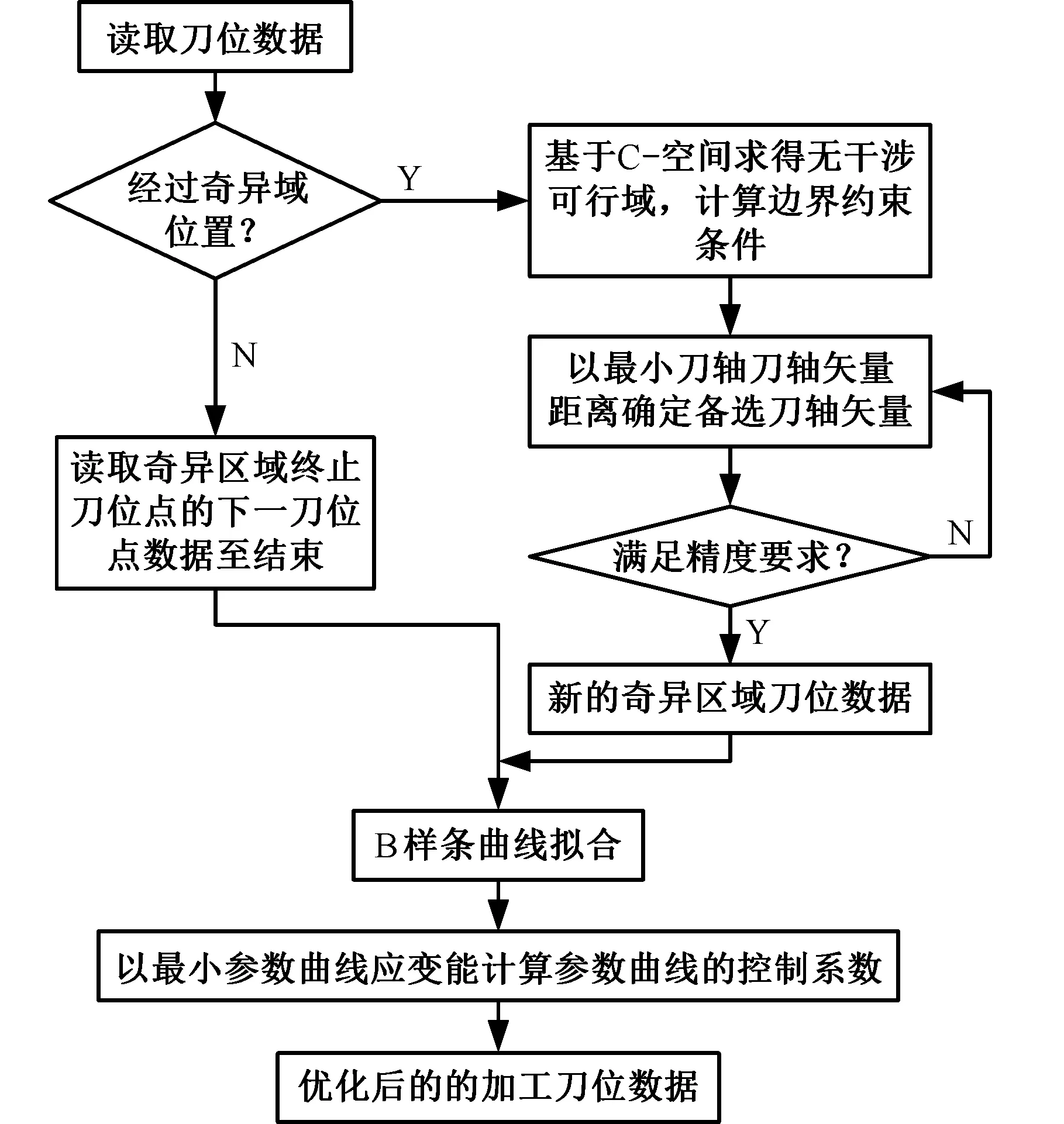
图5 奇异区域处理流程图Fig.5 Flow chart of singular region processing

(3)对更新后的刀轴矢量通过式(7)得到切矢km、kn，同时将km、kn作为边界约束条件，将所有刀轴矢量进行B样条曲线拟合，B样条的光顺程度可表示为

(9)

其中，下标k表示k阶B样条曲线，此处取k=5;M为控制点个数；NM,k(ur)为相应参数ur的基函数值；ΘM为控制系数，可对B样条曲线形状进行修改；εM为控制系数ΘM的偏移量；Φ′ur为控制点偏移后旋转角的角度变化，包含了修改后角度变化的最大刀轴方向。

(4)在满足上述条件之后，以参数曲线应变能最小为优化目标进行刀路优化，最小应变能ΔEmin的表达式如下：

(10)

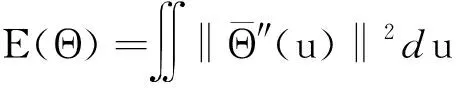
(11)

i=1,2,…，M

其中，旋转轴A1和C1的角速度ωA1,i、ωC1,i满足最大角速度ωmax限制，角加速度αA1,i、αC1,i满足最大角加速度αmax限制，这里速度和加速度通过数值差分格式近似，在式(9)和式(11)的线性约束条件下，式(10)可通过MATLAB的求解器进行优化求解。

(5)根据式(9)、式(10)计算出参数曲线的控制系数得到新的刀位点数据，进而可得到优化路径。

3 实验验证

本文针对双五轴镜像铣削奇异问题提出了刀路优化方法，通过蒙皮加工件的铣削实验来验证该方法的有效性，本实验所使用的机床为图1所示的双五轴镜像铣削加工平台，图6所示为镜像铣削加工控制平台，控制平台可以采集加工数据并导出，其中包括采集时间、滤波前测厚、滤波后测厚、测厚水压、电涡流距离等。本文的刀路设计轨迹连续无抬刀、无交叉，采集时间从起始刀位点进行下刀时开始采集，中间加工过程无抬刀时间，一直到完整路径加工结束后采集时间停止。实验所使用的材料为7075铝合金薄壁件，薄壁件的壁厚为8 mm，切削区域为650 mm×300 mm的型腔，如图7所示。加工实验所使用的刀具为直径16 mm、底刃半径7 mm、圆角半径1 mm、2刃的平底铣刀。本次实验加工目标壁厚为1.2 mm，铣削加工程序段运行三次(即加工该型腔三次)，每次可切深度为0.8～3 mm，如表2所示，并且给定机床的主轴转速为9000 r/min，进给率为2000 mm/min，径向切宽为12.5 mm，加工过程中使用冷却液对加工区域进行冷却。

图6 镜像铣削加工控制平台Fig.6 Mirror milling processing control platform

图7 实验加工件Fig.7 Experimental work piece

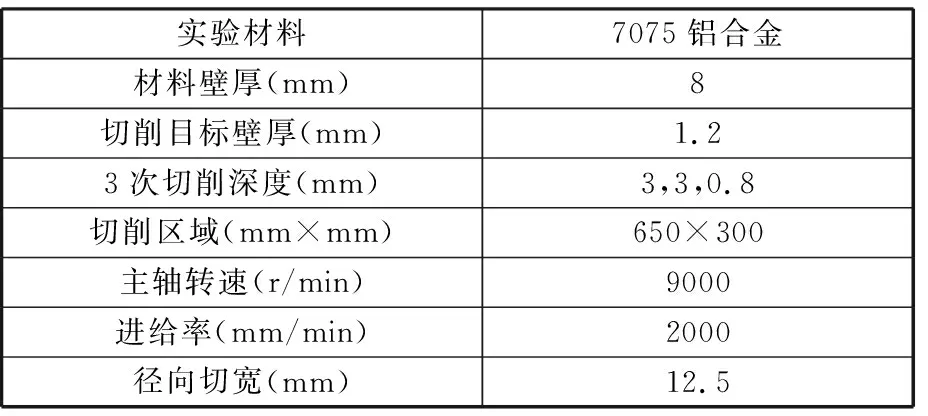
表2 实验参数

本文的实验加工对650 mm×300 mm矩形下陷区域采用先加工外轮廓、后加工内轮廓的方法设计的原始路径，如图8所示，奇异区域优化前和优化后的刀轴矢量对比结果如表3所示。根据文献[13]的方法可以得到奇异区域边界大小为2.0°，即A1≤2.0°的范围为铣削侧加工刀路的奇异区域，图8中红色虚线代表奇异位置1和奇异位置2。基于工艺编制所得到的前置刀位文件进行后处理可以得到铣削侧C轴的运动位置，经处理可得到C轴的旋转变化量，并且可以观察到奇异位置1和奇异位置2的C轴运动发生突变，奇异位置1的C轴旋转变化量达到18.33°/mm，并且奇异位置2的C轴旋转变化量达到13.58°/mm。

图8 原始路径仿真图Fig.8 Original path simulation diagram

表3 奇异位置附近刀位点数据

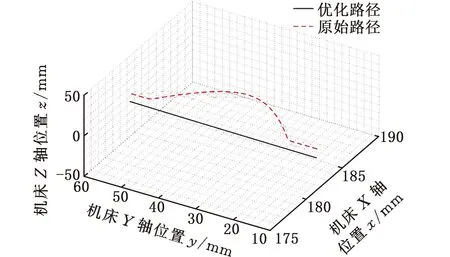
针对该下陷区域奇异问题的存在，采用2.3节所提出的奇异区域刀路优化方法进行优化，在本次实验中，原始路径和优化路径给定的机床、刀具参数相同，路径规划的起始点、终止点以及路径方向相同，如图9所示，可以看到优化路径明显避开了奇异位置，如图10a所示的奇异位置1局部路径和图10b所示的奇异位置2局部路径，且优化结果更加光顺，同时在图11中奇异位置1的C轴旋转量由18.33°/mm下降到了0.13°/mm，奇异位置2的C轴旋转量由13.58°/mm下降到了0.009°/mm。因此本文的奇异区域路径优化方法可以有效地避开奇异区域，并且提高了奇异区域路径的光顺性。

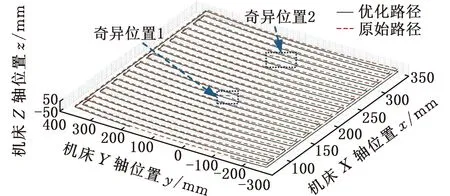
图9 原始路径和优化路径对比Fig.9 Compare the original path with theoptimized path

在实验中，原始路径和优化路径的对比图见图12。在图12a所示原始路径中对应的奇异位置1和奇异位置2，其工件表面存在明显的环状轨迹，这是由于C轴突变快速旋转形成的，出现奇异问题的刀路左侧存在残留的现象，右侧则出现了一定的过切现象；图12a中局部路径的椭圆虚线区域内存在可观察到的残留现象，过切现象通过厚度测量值进行标识。

(a)奇异位置1局部路径

图11 C轴旋转变化量对比Fig.11 Comparison of variation of C-axis rotation

由于旋转轴的运动突变，且在镜像铣削加工特定的约束条件下(即刀轴矢量(i,j,k)与蒙皮工件表面在该刀位点的法向保持一致)，因此当奇异问题出现时刀轴矢量(i,j,k)变化的同时，刀尖点(x,y,z)也会产生变化，从图8中可以看到原始路径的奇异位置出现了偏移现象。在该偏移刀路的左侧会出现残留现象，右侧则出现一定的过切现象，因此会对壁厚产生一定的影响，从而影响表面质量。

与此同时，加工实验中的原始路径和优化路径目标壁厚均为1.2 mm，两次实验中三次切削深度分别保持一致，实验的加工时间、壁厚测量结果和壁厚误差如表4所示，可以看到原始路径和优化路径的壁厚测量范围分别为[1.16,1.32]mm和[1.18,1.23]mm，其壁厚误差分别为[-0.04,0.12]mm和[-0.02,0.03]mm，其完整路径加工时间分别为575.2 s和563.4 s。

综合图12和表4中原始路径和优化路径实验对比结果可以看到，采用本文优化方法后，奇异区域的壁厚误差有所减小且无残留，最小壁厚误差减小50%，最大壁厚误差减小75%，整体壁厚误差范围缩小了68.75%，同时完整的路径加工时间缩短了 2.1%，加工效率和加工质量都得到了提高。

(a)原始路径 (b)优化路径图12 实际加工表面Fig.12 Actual machined surface

表4 实验结果比较

4 结论

(1) 本文通过建立奇异区域边界约束条件以及镜像铣削加工中刀轴矢量与工件表面保持垂直的约束条件，在无干涉可行域的前提下，以最小刀轴矢量距离确定备选刀轴矢量，对奇异区域的刀轴矢量进行局部修正，这样既可以保留原有的刀轴矢量规划的加工特性，又能保证计算效率和加工质量。

(2) 在奇异区域刀轴矢量修正的前提下，对整条加工路径进行B样条曲线的拟合，基于最小参数曲线应变能的目标函数来实现B样条曲线的修改，最小参数曲线应变能可以保证曲线的连续性和光顺性，从而保证了旋转轴运动的连续性，加工效率和质量均得到显著提高。