一种变温环境下水听器灵敏度校准系统的设计

陈思强，李雪健，王月兵，赵 鹏

(1. 中国计量大学 计量测试工程学院，浙江 杭州 310018；2. 国家管网集团西气东输公司 南京计量研究中心，江苏 南京 210046)

1 引 言

近年来，随着人们对海洋的日益重视，对水声探测系统的测量准确性要求越来越高[1]。水听器作为声探测系统的重要组成部分，其灵敏度易受环境的影响，在使用之前需要在不同环境下对水听器的灵敏度进行测量，分析水听器灵敏度的影响因素，从而能实现对水听器灵敏度的补偿以及制作具有更高稳定性的水听器。

在变温条件下,校准水听器灵敏度的传统方法包括耦合腔互易法、振动液柱法、行波管法等[2～5]。耦合腔互易法在测量中需要进行3组换能器的安装和4次转移阻抗的测量,测量过程比较繁琐[6]；振动液柱法校准水听器时虽然操作简单但是受限于腔体体积，在测量尺寸较大的水听器时误差较大[7]，行波管校准水听器灵敏度时，成行波场的过程较为复杂、时间长、校准效率低[8]。

对此，本文设计了一个基于动圈换能器声校准管的水听器灵敏度校准系统，与传统变温环境下校准水听器的方法相比，此系统原理简单、性能稳定、更轻便、可以用于较大尺寸水听器校准并且能够实现待测水听器变温下的灵敏度校准。本文通过波动方程推导以动圈辐射器为振动源的声校准管内的声压分布，计算了温度变化对声管内部声场的影响，进而补偿温度变化对校准结果的影响；通过激光测振仪测量动圈换能器的振动形式并仿真分析底面不均匀振动对声场的影响；仿真分析了腔体内径及壁厚对声场的影响及不同尺寸的水听器对校准的影响，最终确定基于动圈辐射器的声校准管校准系统的具体参数和测量方法，并通过实验验证了系统的可靠性。

2 校准方法与校准装置

2.1 校准方法

基于动圈辐射器声校准管校准水听器灵敏度的基本原理为：底面动圈辐射器不断向声管内发射声波，在声管内形成驻波场，先后将标准水听器与待测水听器的声中心放置到同一位置，测得开路电压，通过式(1)计算待测水听器的灵敏度。

(1)

式中：Mx和M分别为待校准水听器灵敏度和标准水听器灵敏度；px和p分别为待校准水听器灵敏度和标准水听器所处环境的声压；Ux为待校准水听器在声压px作用下产生的开路电压；U为标准水听器在声压p作用下产生的开路电压；Mr为水听器灵敏度基准值，其值为1 V/μPa。

在常温下校准水听器时，由于待测水听器与标准水听器处于相同环境下，此时Mx=M+20 lg(Ux/U)-20 lg(px/p)中的20 lg(px/p)为零。若温度改变，则管中的声压也会随之变化，则在校准水听器的灵敏度随温度变化情况时，有两种解决方法：一是已知一个不同温度下灵敏度的标准水听器，使其能与待测水听器处于同一环境下测量，此时两种水听器所处的声场相同；二是只需知道标准水听器在常温下的灵敏度，在对待测水听器的灵敏度进行变温测量时通过分析温度对测试位置声压的影响，通过公式Mx=M+20 lg(Ux/U)-20 lg(px/p)对校准结果补偿。本文通过第二种方法实现已知标准水听器常温下的灵敏度来校准待测水听器不同温度下的灵敏度。

2.2 校准装置

图1所示为基于动圈辐射器的声校准管法水听器灵敏度校准系统，此系统由动圈辐射器、不锈钢钢管、加热保温模块、信号源、功率放大器、示波器和上位机组成。

图1 测试系统图Fig.1 Measurement system diagram

对于传统的驻波管而言，其激励源一般选用压电换能器，而当发射信号的频率较低时，由于远低于发射换能器的谐振频率，所以在驻波管内声场的信号较弱，不满足管内校准水听器时的信噪比，动圈换能器在低频段内则具有更好的发射特性；并且相对于压电换能器，动圈换能器的温度稳定性更高[9]，更适合在变温校准系统中使用，所以本文采用动圈换能器作为激励源。

信号源发出的信号经过功率放大器后用于激励动圈辐射器向水介质中发出声波，示波器及上位机接到水听器的输出，实现水听器信号的可视化及采集。加热模块主要由K型热电偶、PID温度控制器和加热电路组成。通过实验，此加热保温模块可以实现升温速率>10 ℃/5 min，稳定后介质温度与目标温度的误差不超过±0.1 ℃。

3 温度补偿分析

通过推导校准管内的声压分布公式，分析了温度对测试位置声压的影响，根据不同温度下管内声速与水介质密度的经验公式实现了水听器灵敏度校准的温度补偿。

3.1 声压分布

对腔体建立如图2所示的柱坐标系，以腔体下端面的圆心为坐标原点、以腔体轴线为z轴、以腔体的径向为r轴。图中，H为腔体长度，a为腔体半径，R为动圈辐射器的半径。

图2 系统结构图Fig.2 System structure diagram

由于空气的特性阻抗远小于水的特性阻抗，而不锈钢的特性阻抗远大于水的特性阻抗，因此假定水面为绝对软，不锈钢壳壁为绝对硬。以动圈辐射器的几何中心为原点，建立柱坐标系，则有：

(2)

式中：r为径向坐标;θ为角度坐标;z为轴向坐标;p为腔体内的声压;t为时间变量;c0为水中声速；p|z=H为z坐标为H时的声压值；vz|z=0为水质点在z坐标为0时的振速；vr|r=a=0为径向坐标r为a时的水质点的振速。

腔体内的声场分布与角度无关，使用分离变量法求解式(2)，假设式解的形式为:

p(r,θ,z)=R(r)Z(z)ejωt

(3)

则有：

Z=Acoskzz+Bsinkzz

(4)

R(r)=CJm(krr)

(5)

所以：

p(r,θ,z)=J0(krr)[Acos(kzz)+Bsin(kzz)]

(6)

式中：

(7)

由于vr|r=a=0，则有：

(8)

则：

(9)

p=∑J0(krmr)[Amcos(kzmz)+Bmsin(kzmz)]

(10)

根据式(1)边界条件可得：

p|z=H=0⟹Am=-Bmtan(kzmH)

(11)

根据式(2)边界条件：

(12)

对其按傅里叶贝塞尔级数展开[10]与式(10)对比可得：

(13)

考虑到m=0时，xm(1)=0,此时有J0(0)=1，则有：

(14)

整理得到:

式中：

(15)

*[sin(kzmz)-tan(kzmH)cos(kzmz)]

(16)

式中：p1为主波的声压值；pm是由于圆管内径大于辐射器半径而导致一些波沿着管壁不断反射沿z轴传递产生的高次波的声压值。

3.2 校准结果的温度补偿

根据式(15)可知，由温度变化而引起声管内声压变化的主要因素有动圈辐射器的振速v0、水的密度ρ0以及声速c0，其中动圈换能器的表面振速可以由输入电功率表征，水的密度以及声速随温度变化可以由经验公式直接求取。并且随着温度上升，校准管内相同位置处的声压是不断减小的，因此在温度高于常温时，需要在校准结果的基础上补偿一个正值，而在低于常温时则需要在灵敏度的校准结果上补偿负值。

基于水的密度和声速与温度的关系[11～13,19]，以 20 ℃ 时的校准结果为基准，则500 Hz时温度变化后的补偿曲线如图3所示。

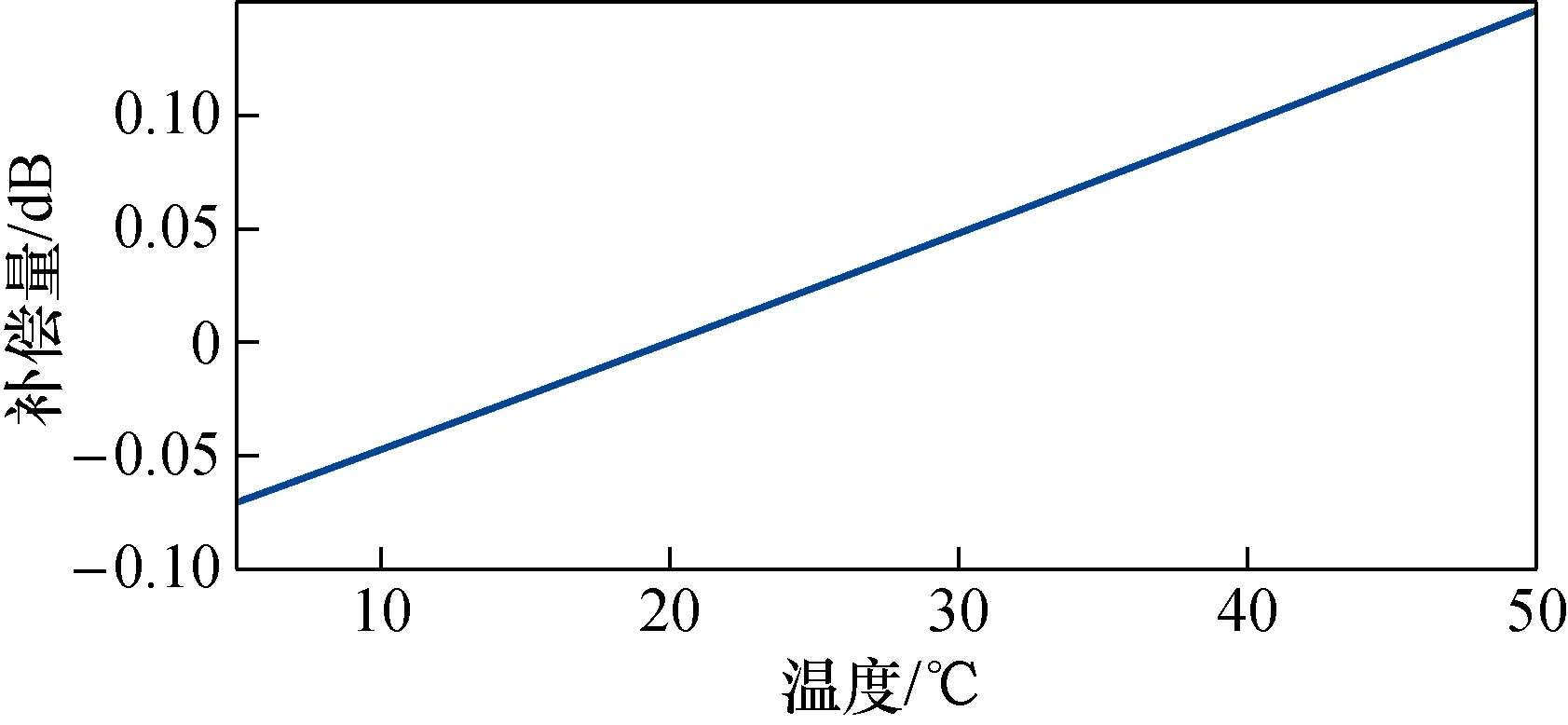
图3 500 Hz时不同温度相对于20 ℃水听器校准结果的补偿量Fig.3 Compensation amount of different temperature relative to 20 ℃ hydrophone calibration result at 500 Hz

由图3可知，管内水介质温度从10 ℃上升到 50 ℃，水听器500 Hz处的灵敏度补偿值约为 0.25 dB，其余频点的温度补偿量可以把管内声速和水密度的经验公式带入式(15)中求得。

综上所述，本章利用解析法与建模法对基于动圈辐射器的声校准管内声场进行计算，分析了温度对声场的影响，最终确定了温度补偿曲线。

4 系统的设计

在此测量系统中，声校准管的尺寸、腔壁的非刚性、动圈辐射器的振动形式和水听器的不同尺寸是影响声场的主要因素，下面通过建立模型和有限元仿真对影响因素进行分析，确定系统的具体尺寸和测量方法，并研究了此系统适合的水听器尺寸。

4.1 声管内径的设计

在动圈辐射器半径R为50 cm时，图4计算了圆管内径在不同尺寸的下，高次波幅值与主波幅值的比值，其值反映了管内声场的纯净性。

图4 R/a对声场纯净性的影响Fig.4 R/a Impact on the purity of the sound field

由图4可知，随着圆管尺寸下降，管内声场的纯净性越来越高，并在a=R时，其内部的高次波为零。在a≤9 cm时，高次波幅值与主波幅值的比值低于1‰，即可忽略管内高次波带来的影响。

4.2 管壁厚度的设计

在对充液管道的研究中，通常把钢管视为刚性壁，但是关于流-固耦合的研究表明，钢的特性阻抗只比水的特性阻抗高一个量级，严格来说不能看作刚性壁，钢管必须看作弹性介质[14～16]。针对此，研究了管壁为非刚性时壁厚对声场的影响。

由式(14)可知，管内的声速和声场均匀性都是影响系统校准精度的因素。对于弹性充液管道内的声场分析，Rubinow和Kelle研究了约束和非约束粘弹性管内的轴对称流体波，给出了传播系数和速度的简化关系和图表[17]，而本系统由于采用的是比较法校准水听器灵敏度，因此主要分析非刚性壁对管内声场均匀性的影响。

图5为Comsol仿真分析内径60 mm不同管道壁厚对声场均匀性的影响。

图5 声场不均匀性与管壁厚度的关系Fig.5 The relationship between the inhomogeneity of the sound field and the thickness of the pipe wall

可以看出，随着厚度提升，声场越来越均匀，在厚度为10 mm之后声场不均匀度的变化趋于平稳，并且此时声场的不均匀度约为10%。考虑到动圈辐射器的尺寸以及与之后加热组件的配合，此处可以选择10 mm厚的不锈钢管。

4.3 校准位置的确定

由于动圈辐射器本身的机械性质，会导致辐射器端面的各点振速不相等，其内部声场不均匀性也会受此影响。

按式(17)设置底面的振动形式，通过Comsol对其仿真可以得到其内部声场。图6所示为由于底面非均匀振动而导致的声场不均匀性与动圈距离的关系。

图6 声场均匀性与深度的关系Fig.6 The relationship between sound field uniformity and depth

由图6可知，由动圈辐射器的不均匀振动而引起的声场不均匀度随着远离动圈而逐渐减小，在 80 mm 处的影响即可忽略。因此在校准过程中水听器的放置位置应高于动圈80 mm。

4.4 水听器尺寸限制

把球形水听器放入20 cm深的水柱中心后，由于水听器的影响，管内的声场也会发生改变。利用Comsol仿真计算100 Hz处管内中轴线上有无水听器时的声压，其结果如图7所示。

图7 有无水听器中心轴线处的声压分布Fig.7 Sound pressure distribution at the central axis of the sound tube with and without the hydrophone

由图7可知，管内放入水听器后，水听器下方的声压变大，若以水听器中心处的声压作为水听器所受到的平均声压，则放入水听器后水听器声中心位置处的声压也会大于未放置水听器时该点的声压。

图8所示是水听器尺寸对声场的影响，差值表示水听器表面的声压级与无水听器时该点处的声压级之差。其中，D为腔体的直径，d为放入的球形水听器的直径。由图可知，水听器尺寸越大，对水中声场的影响越大。在内径为120 mm的声管中，直径为30 mm以下的水听器校准时的由水听器外形引起的声场扰动小于0.2 dB，50 mm以内的小球水听器对水中声场的影响小于0.3 dB，60 mm小球水听器对声场的影响达到0.75 dB，80 mm的小球水听器对声场的影响达到1.6 dB。

图8 水听器尺寸对声场的影响Fig.8 Effect of hydrophone size on sound field

综合上述分析，通过Comsol对声校准管的管壁壁厚、动圈辐射器的振动模式和水听器对声场的影响进行了仿真分析。结果表明：内径120 mm，壁厚为8 mm的声管中心轴线周围60 mm的圆柱空间内其声场不均匀性小于3%，满足使用要求；底面的非均匀振动对于声场的影响可在离动圈辐射器表面 80 mm 后消除；对于30 mm以下的水听器测量结果由水听器尺寸引起的误差小于0.2 dB。

5 校准系统的检查

5.1 底面振动形式测试

通过激光测振仪系统测量辐射器不同径向位置的振动，测量系统如图9所示，得到辐射器沿着径向方向的振动形式为:

a0*(1-0.055*cos(26.2*r′))

(17)

式中：a0表示辐射器不同频率振动的最大幅值；r′为辐射器径向坐标，范围为[0,0.05 m]。

图9 激光测振仪检测动圈振动模式Fig.9 Laser Vibrometer Detects Moving Coil Vibration Mode

5.2 管内声场测试

选择灵敏度为-197 dB的小球水听器测量声管中心轴线上的声压分布，其结果如图10所示。由图可知，声压分布与理论计算结果相一致。

图10 管内声压分布Fig.10 Sound pressure distribution in the tube

5.3 动圈换能器输入功率测试

动圈式换能器的发射输入电功率的计算方法为：

We=UpIpcosα

(18)

式中：Up为动圈辐射器的激励电压；Ip为动圈辐射器的输入电流；α为Up与Ip之间的相位。按照式(18)的计算方法，获得10 ℃与50 ℃时动圈换能器的输入电功率如表1所示。由表1可知：在测量频段内，介质温度从10 ℃与50 ℃后，动圈的输入电功率变化小于1%。

表1 10 ℃与50 ℃时输入电功率值

6 测试结果及分析

为了证明该方法对校准不同类型水听器灵敏度及变温灵敏度校准的有效性，实验中使用了两种待校水听器，一种是常温下30 mm小球水听器的校准实验，另一种是不同温度下圆管水听器的校准实验。

测量步骤：

(1) 调整信号源输出电压及功率放大器的增益，使功率放大器的输出电压为12 V；

(2) 放置标准水听器的声中心于入水10 cm处，测量不同频率下的开路电压U1；

(3) 取出标准水听器，待测水听器的声中心放入水中，应保持待测水听器的声中心与标准水听器的声中心一致，读取开路电压Ux；

(4) 读取水介质此时的温度。

常温下对30 mm小球水听器的校准结果与标准值的对比如图11所示。

图11 常温30 mm小球水听器校准结果与标准值对比Fig.11 Comparison of calibration results and standard values of 30 mm spherical hydrophone at room temperature

由图11可知，常温下，此系统的测量结果与标准值的最大偏差为0.5 dB，小于振动液柱法与本系统测量不确定度的几何平均值0.8 dB，可以证明此系统在常温下对水听器灵敏度校准的有效性。在变温条件下，分别在23 ℃和40 ℃对圆管水听器进行校准，并与振动液柱法校准结果进行了比较，校准结果对比如图12所示。

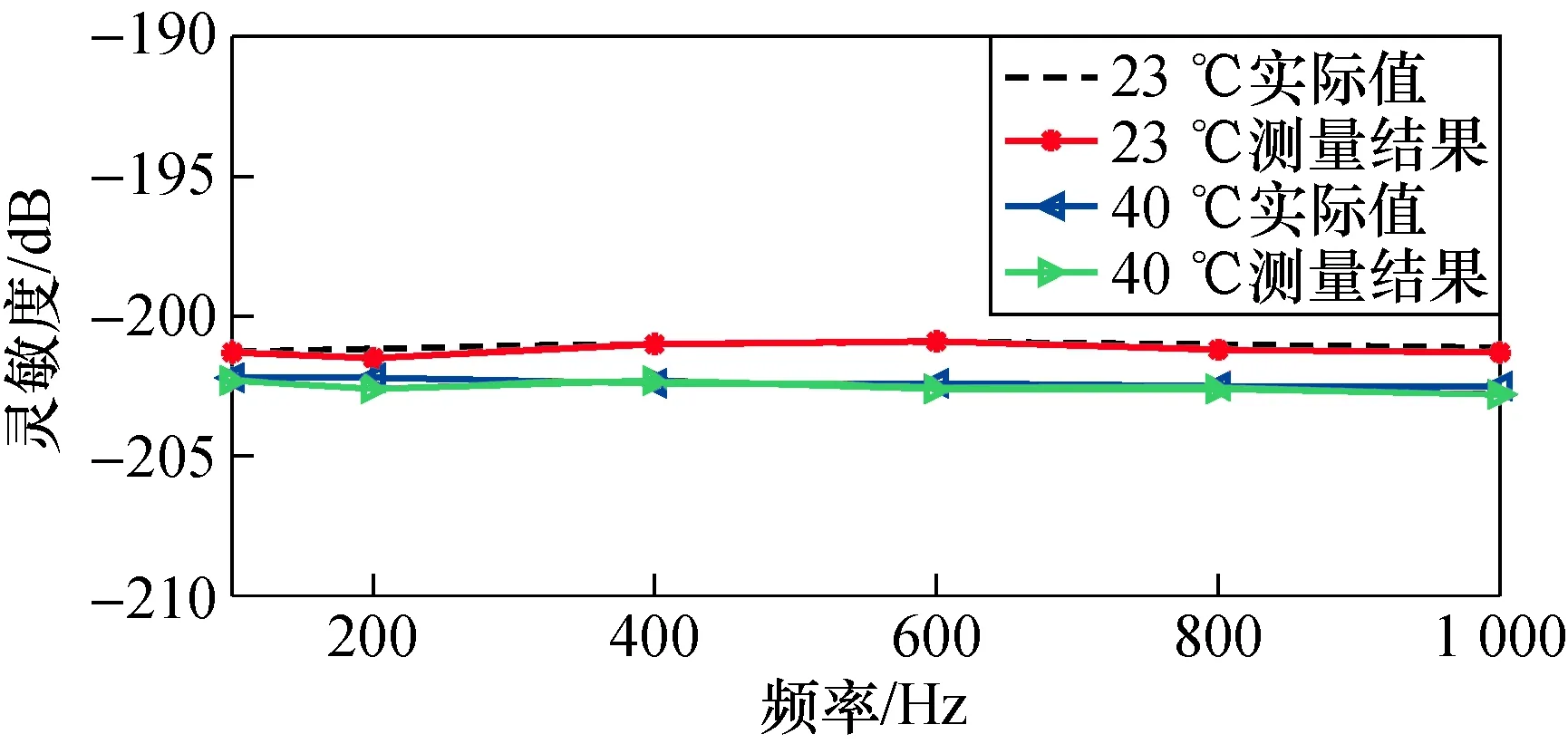
图12 23 ℃及40 ℃下圆管水听器的校准结果与振动液柱法的结果对比Fig.12 Comparison between the calibration results of circular tube hydrophone and results of vibrating liquid column method at 23 ℃ and 40 ℃

由图12可知，在40 ℃温度下两者校准的结果最大偏差为0.6 dB，且测得的水听器灵敏度曲线较为平滑，最大偏差值小于振动液柱法与本系统测量不确定度的几何平均值0.8 dB，可以证明此系统在不同温度下对水听器灵敏度校准的有效性。

由上述实验结果可以证明，基于动圈换能器的声校准管中采用比较法校准水听器灵敏度的方法是可行的，由于该方法采用的声校准管的尺寸可以比振动液柱腔体尺寸更大，可以实现较大尺寸水听器灵敏度的校准。

7 不确定度分析

测量系统的不确定度由两类组成，一类由重复性测量引入，可以通过统计方法进行评定，称为测量不确定度A类评定。另一类由测量系统本身或测量方法不完善等因素引入，可以通过理论和经验分析的方法进行评定，称为测量不确定度B类评定[18]。在该校准方法测量不确定度A类评定研究中，用100～1 000 Hz的圆管水听器的灵敏度为例进行分析，通过对样品进行6次独立测量(n=6)，结果如表2所示。以测量平均值的实验标准偏差作为系统测量不确定度A类评定uA，由式(18)计算。

(19)

表2 系统重复性实验结果Tab.2 System repeatability test results

系统的测量不确定度B类评定分量主要来源于：(1)待测水听器和标准水听器声中心不重合；(2)待测水听器与标准水听器对声场的影响不同；(3)动圈辐射器振动导致的入水深度的改变；(4)功率放大器稳定性；(5)标准水听器的灵敏度测量不确定度；(6)人为因素引入不确定度分量等。系统的B类不确定度分量具体数值如表3所示，为方便表示，各个分量仅以数字代表。

表3 B类不确定度分量数值Tab.3 Type B evaluation of measurement uncertainty values

估算系统的测量不确定度B类评定为：uB=0.5 dB。通过扩展测量不确定公式(20)：

(20)

计算扩展不确定度为：U=1.0 dB(k=2)。

8 结 论

本文通过建立模型分析声校准管内的声压分布，并计算了变温后对灵敏度校准结果的补偿量；利用Comsol仿真分析与理论计算，确定了合适的声管尺寸和测量方法,最终实现了对水听器灵敏度在变温环境下的低频校准并说明了该方法在校准较大尺寸水听器及在变温环境下校准水听器的可行性。通过分析影响此灵敏度校准系统校准精度的主要因素，估计基于动圈换能器的声校准管的变温水听器灵敏度校准系统校准水听器灵敏度的扩展测量不确定度U=1.0 dB(k=2)。