多辐射器航天器热控流体回路布局的(火积)耗散分析

刘 欣，梁新刚

(1.清华大学航天航空学院，北京 100093；2.中国运载火箭技术研究院，北京 100076)

0 引 言

近年来，随着航天器功能任务的增强，对热控系统的控温能力和控温精度提出了越来越高的要求。单相流体回路技术作为一种成熟可靠的热控措施在航天器热控系统设计中得到了越来越多的应用。流体回路热控系统具有载热能力强、布局灵活、传热距离远的优点，可以收集航天器内仪器设备工作时产生的热量，并传输到辐射器，最终通过辐射器向空间排散。

目前，围绕流体回路热控系统开展的研究主要集中在系统的集成设计[1-2]、流体回路的工质选择[3-4]、流体回路的控制方法[5-6]、流体回路辐射器的参数设计[7-8]以及流体回路在航天器舱内的布局优化[9-10]。而对于舱体结构复杂的航天器，为了适应航天器的结构布局，辐射器往往被分为多个面板，安装于航天器的不同位置。由于每个辐射器的位置不同，其吸收的空间外热流也各不相同。采取何种方式，将流体回路与辐射器连接在一起，优化流体回路的散热过程，提高流体回路的散热效率，也是航天器热控系统设计中需要重点考虑的问题之一。

对于传热过程的优化，过增元等[11]基于热学与电学的类比，提出了一个新概念——(火积)，并在传热能量守恒方程的基础上推导了(火积)平衡方程，发展了(火积)耗散极值原理，在给定约束条件下，当耗散为极值时，热量传递效率最高，系统传热过程最优。程雪涛等[12]证明了在孤立系统的自发传热过程中，系统的(火积)总是减小的，指明了传热过程的发展方向。(火积)和(火积)耗散极值原理在传热优化问题中得到了较为广泛的应用[13-17]。将(火积)理论与航天器热控设计相结合，可为航天器热控设计的工程优化提供明确的方向。吴晶[18]、程雪涛[19]、刘欣等[20]，基于(火积)理论对辐射换热过程及空间辐射器优化进行了分析，指出在空间辐射器设计中，温度均匀化是一个重要的设计原则。程雪涛等[21-22]针对热控流体回路中电子设备并联网络流量分配与面积分配的优化问题，利用(火积)理论进行了分析和讨论。这些研究表明(火积)和(火积)耗散极值原理在分析航天器传热优化问题中具有较好的适用性。

本文运用(火积)理论，分别对流体回路串联、并联多辐射器的散热过程进行了分析研究，并针对具体算例进行了数值计算，研究结果对航天器流体回路与辐射器的布局设计及散热优化具有指导意义。

1 流体回路散热过程(火积)耗散分析

假设航天器受结构布局的限制，舱体外设计了m块辐射器，热控流体回路需要将航天器舱内设备产生的热量传输至辐射器向空间排散。流体回路可以采用串联和并联两种方式与辐射器进行连接。

1.1 串联辐射器流体回路的(火积)耗散分析

采用流体回路串联辐射器的形式时，散热工质按先后顺序，依次流过m个辐射器，如图1所示。图中Tin为进入辐射器的流体工质温度；Tout为经辐射器散热冷却后流出辐射器的工质温度；Rk表示辐射器，下标表示辐射器的编号；q为流体回路中工质的质量流量。

图1 流体回路与辐射器串联连接
Fig.1 Fluid loop connected in series with multiple radiators

对于每一个辐射器，流体管路平行布置于辐射器中，管间距为2

L

h

。散热工质沿流道通过辐射器时，将热量传递给辐射器向空间散出。假设流体管路通过辐射器的长度为

L

；沿流体管路将每个辐射器分为

n

个散热的微元段，每个微元段的长度为

L

/

n

。如图2所示，流体工质流过第

k

个辐射器上第

i

个微元段散出的热量为

Q

k,i

。

图2 每个辐射器微元散热Fig.2 Heat dissipation of radiator microelements

流体工质流入微元段时的温度为Tk,i-in；流出微元段的温度为Tk,i-out。工质流过每个微元段散出的热量Qk,i为：

Qk,i=cq(Tk,i-in-Tk,i-out)

(1)

式中,c为工质比热,流过微元段的流体平均温度Tk,i为：

(2)

流体的热量通过对流换热传递给管壁，则有：

Qk,i=shk,i(Tk,i-Th,k,i)=

(3)

式中，s为微元段流体管路面积,hk,i为流体与管壁间的对流换热系数,Th,k,i为微元段的流体管路壁温。

在式(3)中，流体管路管壁的温度Th,k,i不仅与流体温度有关，还与辐射器吸收的空间热流有关，如果辐射器两面均可进行散热，且航天器舱体对辐射器没有遮挡，散热量可以表示为

(4)

式中，qf为辐射器表面吸收的空间热流密度；Lh为肋片半宽；ηk,i为辐射器微元段肋效率，ηk,i的计算可参考文献[23]。

流体在辐射器微元段进行散热时，进入微元段的(火积)流Gk,i-in，为[11]：

(5)

输出微元段的(火积)流Gk,i-out，为[11]：

(6)

流体流过微元段的(火积)耗散为

Tk,i-out)(Tk,i-in-Tk,i-out)-Qk,iTh,k,i

(7)

把式(1)整理后代入式(7)，可得：

(8)

把式(3)整理后代入式(8)，可得

(9)

流体流过单个辐射器的(火积)耗散Φk，为：

(10)

串联回路，流体管路流过所有辐射器的(火积)耗散Φs，为

(11)

每个微元散出热量占辐射器总散热量的比例为xk,i

(12)

式(11)可表示为

(13)

流体回路优化的目标是要提高流体回路散热效率，降低流体回路散热温度。根据(火积)耗散极值原理[11]，当(火积)耗散最小时，系统传热过程最优。因此，系统的优化问题可以用(火积)耗散来表示

(14)

采用Lagrange乘子法求流体回路散热过程的(火积)耗散极值，建立如下函数：

(15)

其中，λ为拉格朗日乘子。为了求极值，对该式对xk,i求偏导，并令其等于0

(16)

将式(12)代入式(16)整理得

(17)

将式(3)整理后代入式(17)可得

(18)

式(18)为流过微元段流体的平均温度与流体管路壁温的差。当式(18)为常数时，表明流体回路的流体与管路壁面之间的传热温差达到均匀，而此时流体回路散热的(火积)耗散最小，传热过程最优。

1.2 并联辐射器流体回路的(火积)耗散分析

除了串联的连接方式外，辐射器还可以以并联的形式连接，如图3所示。温度为Tin、流量为q的流体工质被分配到m个辐射器，每个辐射器分配的流量为qk(1≤k≤m)，工质经过辐射器散热后汇合，汇合后的温度为Tout。

图3 流体回路与辐射器并联连接Fig.3 Fluid circuit connected in parallel with multiple radiators

流体流过并联辐射器系统的(火积)耗散由两部分组成，一部分为流体流过辐射器散热引起的(火积)耗散Φs，这一部分(火积)耗散的分析与前面串联回路一样；另一部分为经过辐射器后汇合的流体，汇合过程的(火积)耗散Φh。

(19)

并联回路总的(火积)耗散Φp，为

(20)

每个辐射器分配的流量占总流量的比例为yk

(21)

式(20)可改为

(22)

同样，根据(火积)耗散极值原理[11]，当流体回路系统散热量一定，并联系统传热过程的优化问题可以用(火积)耗散来表示

(23)

采用Lagrange乘子法建立函数

(24)

Φp取极值的条件为

(25)

求解可得：

(26)

Tk,n-out=const

(27)

由于流体进入每个辐射器的温度是相同的，满足式(26)的情况下式(27)也是满足的。因此，对并联辐射器而言，流体回路的流体与管路之间传热温差均匀，流体流进、流出辐射器的温度相同时，流体回路散热的(火积)耗散最小。

2 热控流体管路布局分析

假设一个航天器在高度为400 km的轨道运行，舱内仪器设备工作时产生的热量约为1 kW，在舱体左右两侧伸出两块面积为1.5 m2的辐射器向空间进行散热。辐射器为蜂窝平板，厚度为20 mm，蜂窝板表面覆盖有厚度为1.5 mm的铝蒙皮。流体管路内埋于蜂窝板内，每个辐射器内流体管路长度为10 m，管路直径为10 mm，材质为铝，管路之间的距离为150 mm。采用乙二醇水溶液作为工质，工质流量为4.167×10-5m3/s，工质物性如表1所示

表1 工质物性Tabie 1 Thermal physics properties of glycol

辐射器表面喷涂白漆，涂层的太阳吸收率α为0.39，红外发射率ε为0.87。由于安装位置不同，辐射器受到的空间热流也不相同。由于辐射器离航天器结构舱体较远，某一段时间内，位于航天器左侧的辐射器吸收的空间热流为380 W，位于航天器右侧的辐射器吸收的空间热流为160 W。左侧辐射器面临的散热环境比右侧辐射器更为恶劣。

2.1 流体回路与辐射器采用串联方式连接

当流体管路采用串联的方式与辐射器连接在一起时，有两种连接方案。方案1流体工质先进入吸收空间热流较高的左侧辐射器进行散热后再进入吸收空间热流较小的右侧辐射器散热，如图4所示；方案2与方案1相反，流体工质先进入吸收空间热流较小的右侧辐射器散热后再进入吸收空间热流较高的左侧辐射器散热。

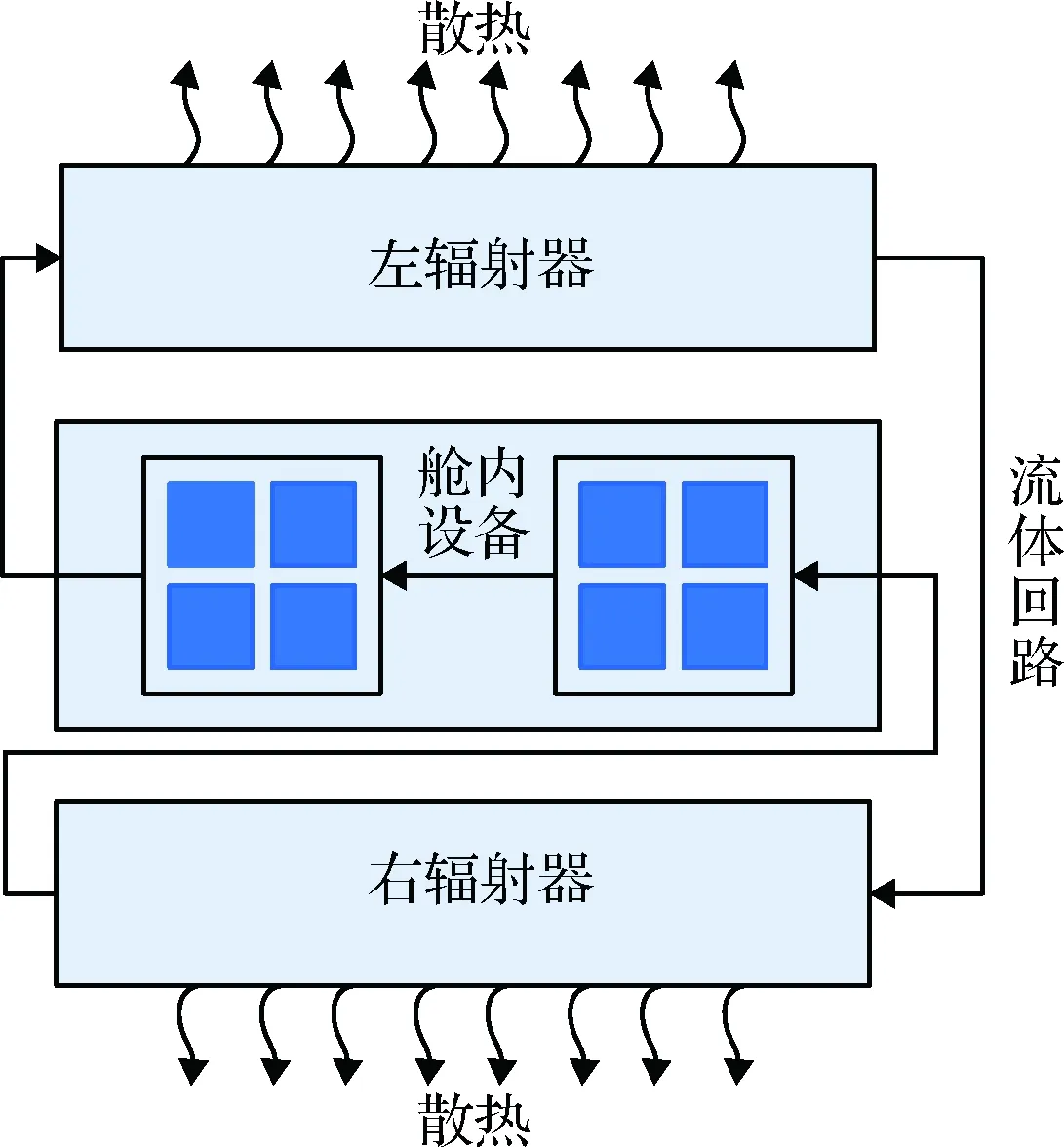
图4 流体回路串联2个辐射器Fig.4 Fluid loop in series with 2 radiators

当流体回路系统在空间达到散热稳定后，不同辐射器散出的热量如表2所示。

表2 不同辐射器散出热量Table 2 Heat dissipation of different radiators

从表2中可以看出，吸收空间热流较小的辐射器，散出的热量较多。由于左右两个辐射器吸收的外热流各不相同，当流体回路串联辐射器的先后顺序不同时，每个辐射器散出的热量也各不相同。相比较而言，方案1中流体回路先流过吸收空间热流较多的辐射器，再流过吸收空间热流较少的辐射器时，两个辐射器散出的热量相对较为均衡。

定义温差均匀性因子φ对流体工质流过辐射器的散热过程进行进一步分析。

(28)

当工质流体与管路之间温差完全均匀时，温差均匀性因子φ=1；当流体与管路之间温差不均匀时，φ<1，不均匀程度越大时，φ值越小。

采用方案1的连接顺序，流体工质按照先左后右的顺序流体辐射器时，流体温度与辐射器管路温度的变化如图5所示。

图5 辐射器工质及管路温度(方案1)Fig.5 Radiator working fluid and pipeline temperature (Scheme 1)

`采用方案2的连接顺序，流体工质按照先右后左的顺序流过辐射器时，流体温度与辐射器管路温度的变化如图6所示。

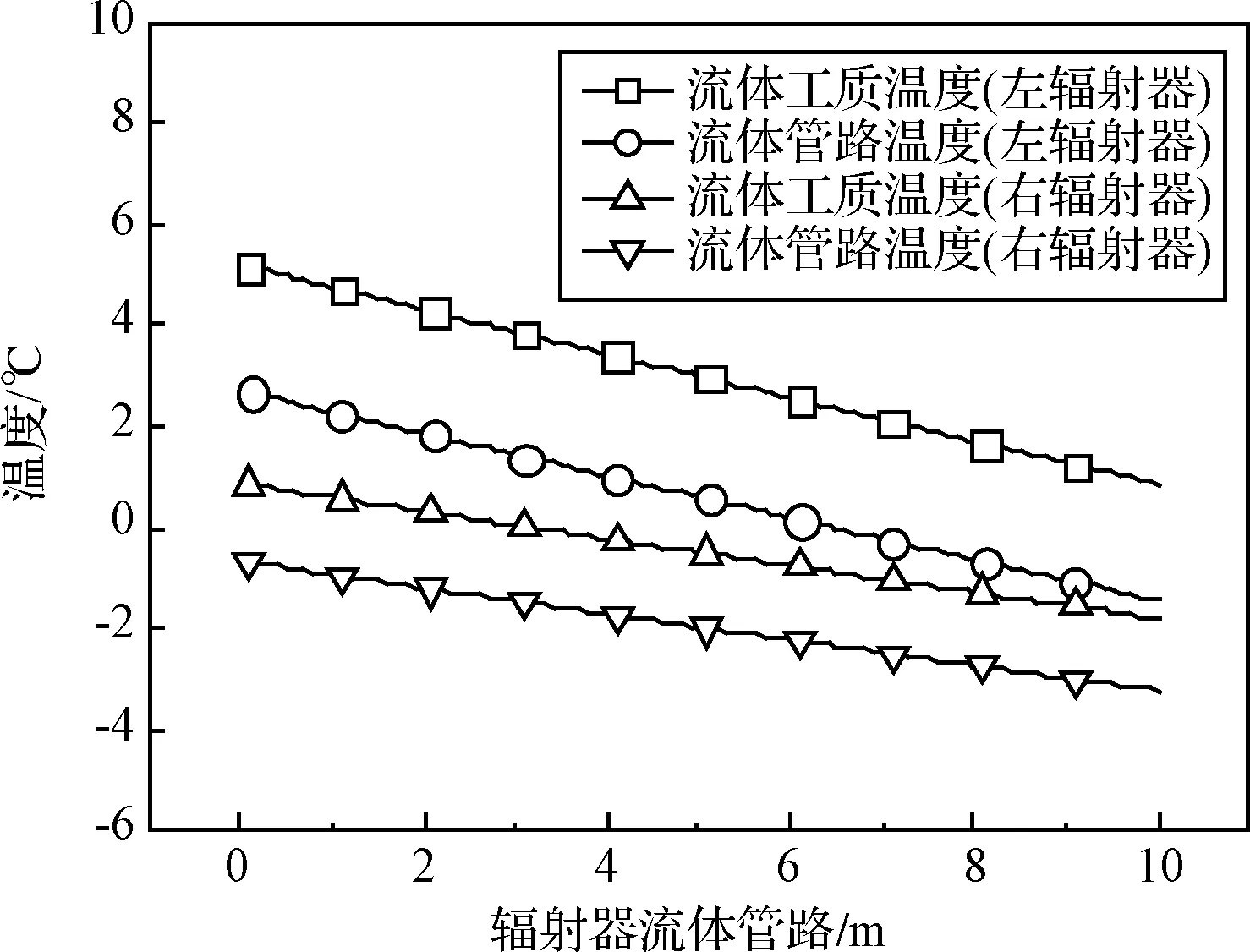
图6 辐射器工质及管路温度(方案2)Fig.6 Radiator working fluid and pipeline temperature (Scheme 2)

对不同串联方案的温差均匀性和(火积)耗散进行分析比较，结果如表3所示。从表中可以看出，采用方案1的串联形式时，流体工质与管路之间的传热温差均匀性更好，(火积)耗散更低。因此，方案1的散热过程更优。

表3 温差均匀性与(火积)耗散比较Table 3 Comparison of temperature uniformity and entransy dissipation

表4为不同串联方案时，流体回路工质温度比较。与表3比较可以发现，采用方案1系统(火积)耗散最小，传热过程最优时，散出相同热量时，流体工质的温度最低。

表4 流体工质温度比较Table 4 Comparison of fluid temperature

采用串联的形式将两个辐射器连接在一起时，根据辐射器吸收空间热流的大小，流体工质按照吸收热流从大到小的顺序依次串联辐射器时，流体回路的散热过程最优，所需流体回路的温度水平最低。显然更低的辐射器出口温度有利于舱内设备的温度控制。

2.2 流体回路与辐射器采用并联方式连接

当流体管路采用并联的方式与辐射器连接在一起时，如图7所示，流体工质经分配后分别进入左、右辐射器进行散热，散热后的工质再汇合为一股流体进入设备舱进行热量收集。

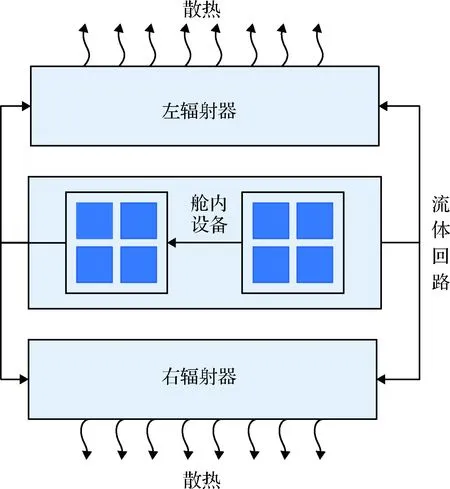
图7 流体管路并联2个辐射器Fig.7 Fluid loop in parallel with 2 radiators

不同流量分配比例情况下，左右两个辐射器的散热量如图8所示。从图中可以看出，一方面，流过辐射器的流体流量越大，辐射器散出的热量越多。另一方面，相同流量情况下，辐射器吸收的空间热流越小，辐射器散热的环境越好，散出的热量越多。

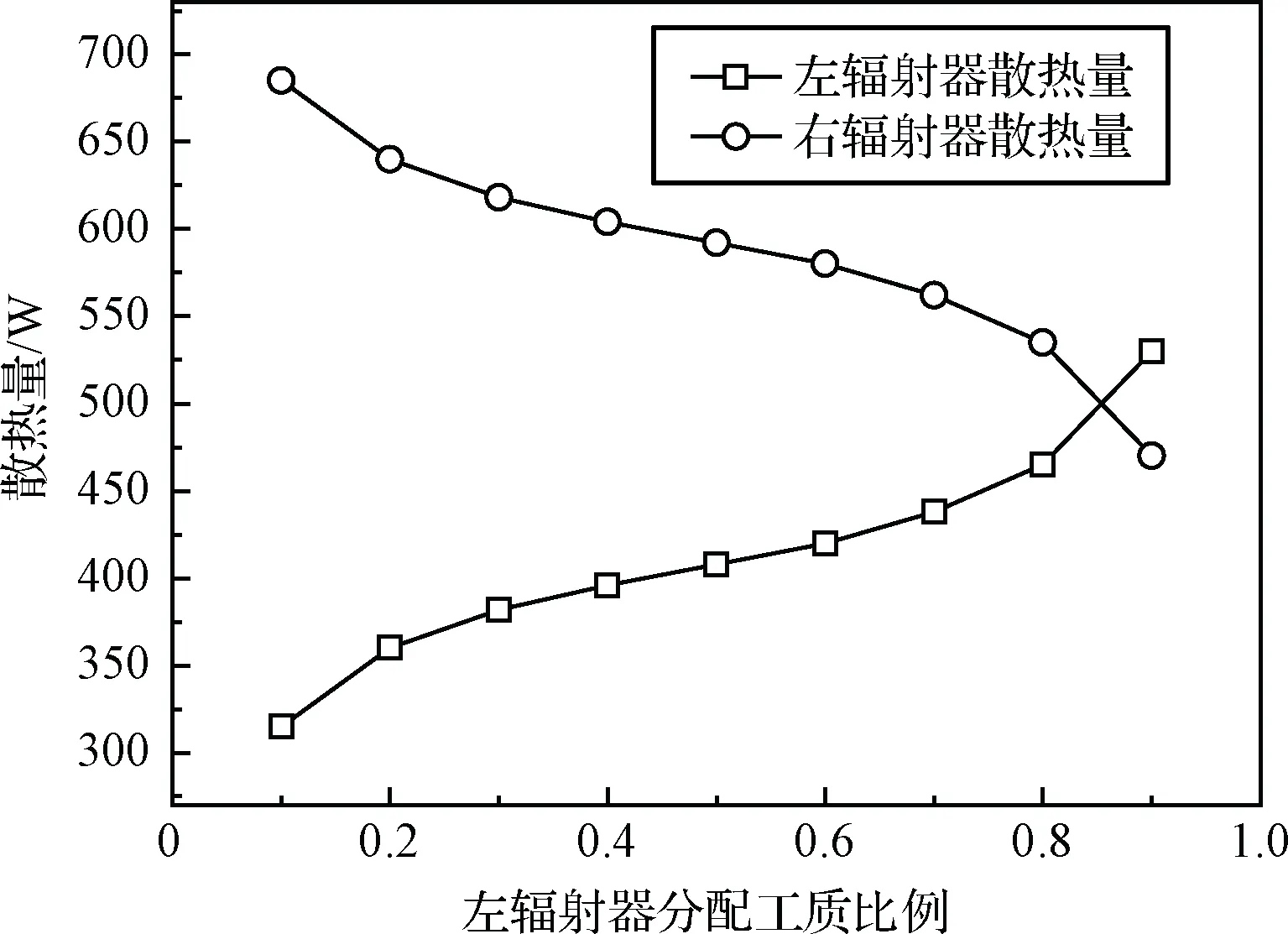
图8 辐射器散热量比较Fig.8 Radiator heat dissipation comparison

采用式(28)计算并联散热系统的流体工质与管路之间的温差均匀因子，结果如图9所示。图10为并联系统流体工质散热过程的(火积)耗散比较。从图中可以看出，左侧辐射器分配工质比例为0.4，右侧辐射器分配工质比例为0.6时，流体与管路之间温差均匀性最好，流体散热过程的(火积)耗散达到最低3415 W·K，系统的散热最优。

图9 流体与管路之间温差均匀因子Fig.9 Uniform factor of temperature difference between fluid and pipeline

图10 并联散热过程(火积)耗散Fig.10 Entransy dissipation in parallel heat dissipation process

不同流量分配比例情况下，流入辐射器的流体温度及流出辐射器混合后的流体温度如图11所示。从图中可以看出，调节流过辐射器的工质的分配比例，流体回路系统的温度水平有一个最低值。与(火积)耗散计算结果相对应，当左、右辐射器分配流体比例为4∶6，流体工质散热过程的(火积)耗散最小时，工质的温度水平也达到最低，流入、流出辐射器的流体温度分别为5.61 ℃与-1.38 ℃。

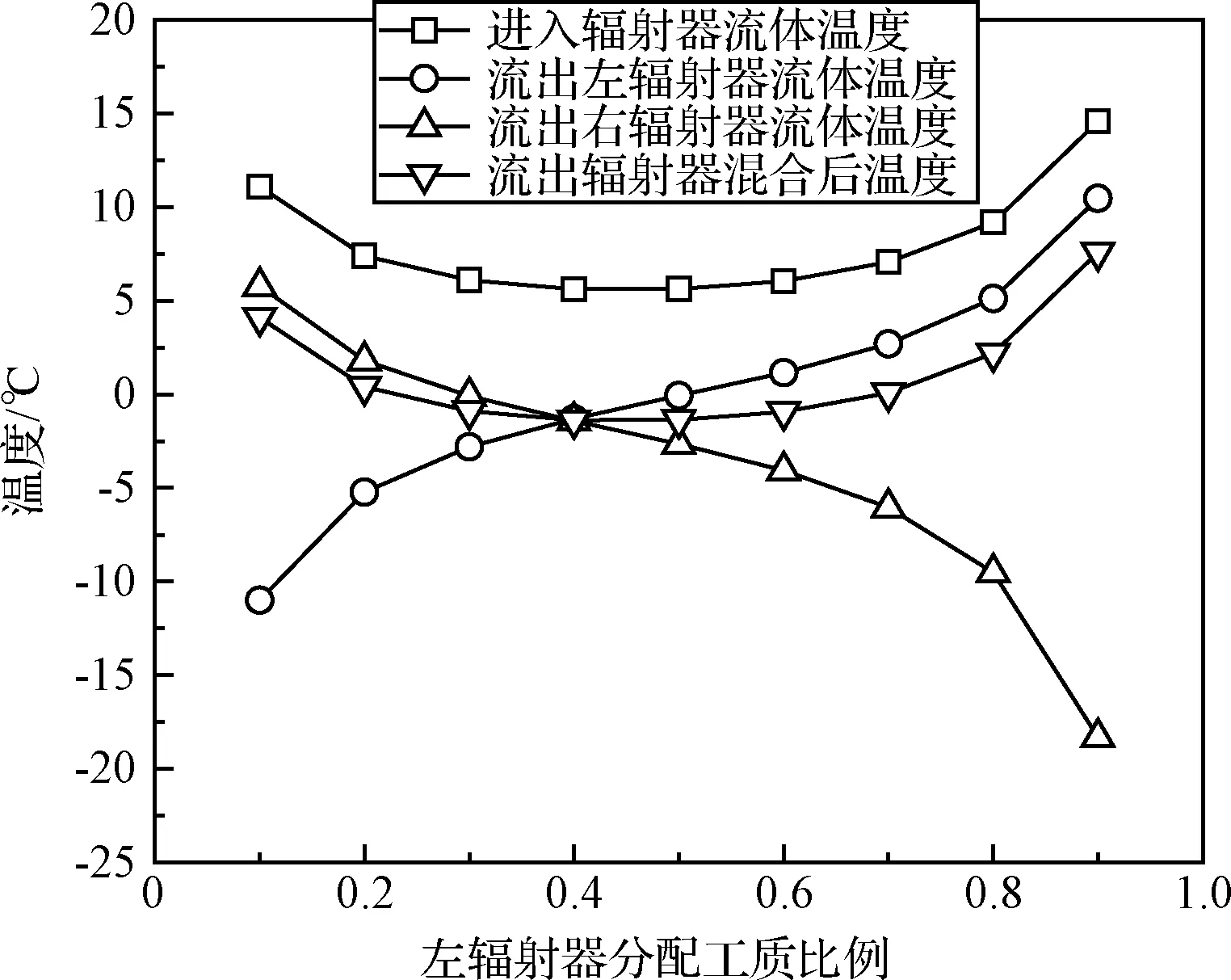
图11 不同流量分配比例时流体工质温度Fig.11 Fluid working temperature at different flow distribution ratios

因此，对于采用并联方式连接辐射器时，可以通过调节流进每个辐射器的流体工质比例，提高工质与散热管路之间的温差均匀性，减少(火积)耗散损失，达到优化散热过程，降低系统散热温度的目的。

2.3 串联布局与并联布局比较

将串联方式的计算结果与并联方式的计算结果相比较可以发现。流体回路系统散出的热量相同时，并联系统流体回路散热过程的(火积)耗散要大于串联系统的(火积)耗散。并联系统的温度水平也要高于串联系统。因此，对于本文航天器的运行工况，采用串联方式将辐射器连接起来进行散热更优。

3 结 论

本文运用(火积)耗散理论对于多辐射器采取不同连接方式的热控流体回路的散热进行了分析，并针对具体案例进行了比较，结果表明：

1)将(火积)耗散极值原理用于分析航天器热控流体回路散热优化问题，具有较好的适用性；

2)散热量不变的情况下，当流体工质与散热管路之间的温度均匀性最好时，流体回路散热过程(火积)耗散最小，系统散热过程最优，散出相同热量时，流体温度最低；

3)对于串联方式，按照辐射器吸收空间热流从大到小的顺序进行连接，回路流体温度最低；对于并联系统，通过调节流过辐射器的工质流量，使流出辐射器的工质温度相等时，系统最优，回路流体温度最低；

4)排散相同热量，流体回路采用串联辐射器的方式时，系统散热性能优于流体回路并联辐射器的方式，回路流体温度更低。