排列组合二项式定理综合测试卷（B卷）答案与提示

一、选择题

1.C 2.C 3.C 4.D 5.C 6.B 7.D 8.A 9.C 10.C 11.D 12.C 13.D 14.C 15.D

17.D

18.A 提示:从正方体的8个顶点中选取4个顶点有C48种情况,正方体表面四点共面不能构成四面体有6种情况,正方体的六个对角面四点共面不能构成四面体有6种情况,所以可得到的四面体的个数为

19.A

20.D

21.C 提示:根据题意,设A={只会划左桨的3人},B={只会划右桨的3人},C={既会划左桨又会划右桨的2人},据此分3种情况讨论:

①从A中选3人划左桨,划右桨的在B∪C中剩下的人中选取,有=10(种)选法;

②从A中选2人划左桨,C中选1人划左桨,划右桨的在B∪C中剩下的人中选取,有选法;

③从A中选1人划左桨,C中选2人划左桨,B中选3人划右桨,有=3(种)选法。

则共有10+24+3=37(种)不同的选法。

22.D 提示:根据题意分步完成任务:第一步,完成3号区域,从6种颜色中选1种涂色,有6 种不同方法;第二步,完成1 号区域,从除去3 号区域的1 种颜色后剩下的5种颜色中选1种涂色,有5种不同方法;第三步,完成4号区域,从除去3、1号区域的2种颜色后剩下的4 种颜色中选1 种涂色,有4种不同方法;第四步,完成2 号区域,从除去3、1、4号区域的3种颜色后剩下的3种颜色中选1种涂色,有3 种不同方法;第五步,完成5号区域,从除去1、2号区域的2种颜色后剩下的4种颜色中选1种涂色,有4 种不同方法;第六步,完成6号区域,从除去1、2、5号区域的3种颜色后剩下的3种颜色中选1种涂色,有3种不同方法。

所以不同的涂色方法数为6×5×4×3×4×3=4 320。

23.C

24.B 提示:由题意知,组成四位“回文数” 。当由一个数组成回文数时,在6 个数字中任取1个,有种方法。当由两组相同的数组成回文数时,在6个数字中任取2个,有种方法,在6个数字中任取2 个时,前两位互换位置又可以组成另一个数,故2 个数组成回文数的个数为,即在6个数字中任取2个组成回文数的个数为。综上,有数字1,2,3,4,5,6可以组成4位“回文数”的个数为

25.B 提示:第一、第二或第六、第七为空位时,第三个空位有4 种选择;第二、第三或第三、第四或第四、第五或第五、第六为空位时,第三个空位有3种选择。

27.D 提示:因为甲和乙必须去同一家企业实习,则将甲乙捆绑作为一个整体。

则共有4 组人需要安排到3 家企业实习,将四组人分为3组,则为1,1,2。

因为出现重复的一组,所以总的安排方法数为

29.C 提示:如图1,分以下几种情况:棱柱侧棱与底面边之间所构成的异面直线有3×2=6(对);棱柱侧棱与侧面对角线之间所构成的异面直线有3×2=6(对);底面边与侧面对角线之间所构成的异面直线有6×2=12(对);底面边与底面边之间所构成的异面直线有3×2=6(对);侧面对角线与侧面对角线之间所构成的异面直线有6(对)。所以共有6+6+12+6+6=36(对)。

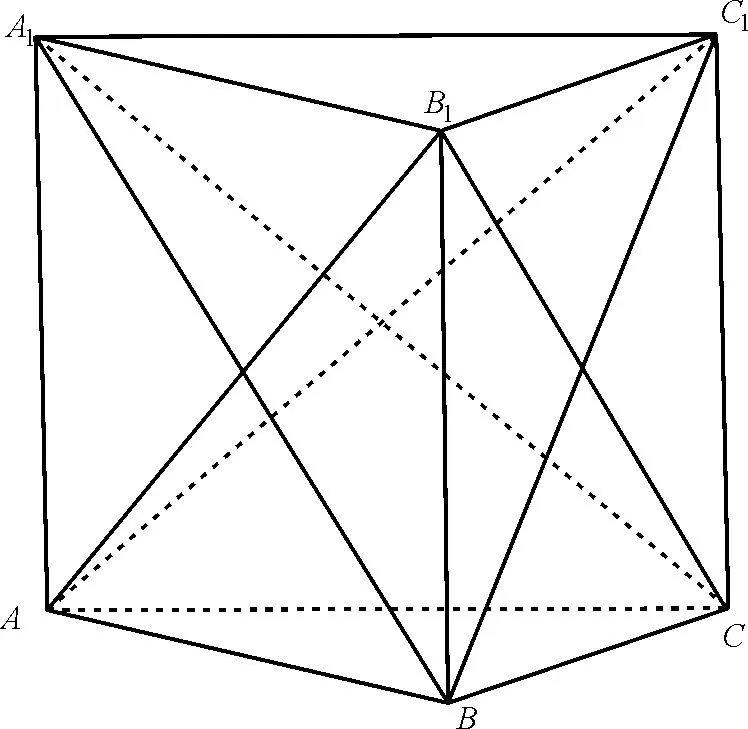
图1

30.B

二、填空题

31.10 32.144 33.1 260 34.192 35.44 36.1 37.41 38.315 39.36 40.1 920 41.1 42.22

43.20 提示:根据题意,分两种情况;若A与C之间为B,即B在A,C中间且3人相邻,共有=2(种)排法,将3人看成一个整体,与D,E两人全排列,共有=6(种)排法,则此时有2×6=12(种)排法;若A与C之间不是B,先从D,E中选取1人,安排在A,C之间,有=2(种)排法,此时B在A的另一侧,将4人看成一个整体,考虑之前的顺序,有=2(种)排法,将这个整体与剩下的1人全排列,有=2(种)排法,此时有2×2×2=8(种)排法。所以总共有12+8=20(种)排法符合题意。

44.454

45.930 提示:若甲、乙都入选,则从其余6人中选出2人,有=15(种)方法。男生甲不适合担任学习委员,女生乙不适合担任劳动委员,则有方法,故共有15×14=210(种)方法。若甲不入选,乙入选,则从其余6 人中选出3 人,有=20(种)方法,女生乙不适合担任劳动委员,则有方法,故共有20×18=360(种)方法。若甲、乙都不入选,则从其余6人中选出4人,有=15(种)方法,再全排,有=24(种)方法,故共有15×24=360(种)方法。综上所述,共有210+360+360=930(种)方法。

46.2n提示:每次传球有2种方法,所以n次传球之后,共有2n种可能的传球方法。设n次传球之后,足球回到文同学脚下的传球方法为an种。

三、解答题

(2)就甲、乙2名同学中实际参与演讲比赛的人数进行分类计数:

第一类,甲、乙2名同学中实际参与演讲比赛的恰有1 人,满足题意的不同的演讲顺序的种数为

第二类,甲、乙2名同学中实际参与演讲比赛的恰有2 人,满足题意的不同的演讲顺序种数为

因此满足题意的不同的演讲顺序的种数为960+180=1 140。

50.(1)根据题意,若恰在第5 次测试后就找出了所有次品,即第5 次测试的产品恰为最后一件次品,另3件在前4次中出现,则前4 次有一件正品出现,所以共有不同的测试方法。

(2)根据题意,分三步进行分析:先排第1次测试,只能取正品,有6种不同的测试方法,再从4件次品中选2件排在第2次和第7次的位置上测试,有=12(种)测试方法,最后排余下4 件的测试位置,有(种)测试方法。所以共有6×12×240=17 280(种)不同的测试方法。

52.根据题意可分为如下几类比赛:

(2)八分之一淘汰赛,8 个小组的第一、二名组成16 强,根据抽签规则,每两个队比赛一场,可以决出8强,共有8场;

(3)四分之一淘汰赛,根据抽签规则,8强中每两个队比赛一场,可以决出4强,共有4场;

(4)半决赛,根据抽签规则,4 强中每两个队比赛一场,可以决出2强,共有2场;

(5)决赛,2强比赛一场确定冠亚军,4强中的另两队1场决出第三、第四名,共有2场。

55.(1)按照最左端分两类,第一类,先排甲,其余的5人全排列,共有=120(种)方法;第二类,先排乙,最右端不排甲有=4(种)方法,其余4人全排列,有=24(种)方法,共有=96(种)方法。由分类计数原理得共有120+96=216(种)方法。

(2)分步完成,第一步,将A,B捆在一起当作一个元素与除C外的两个元素一起全排列,共有)方法;第二步,将C插入已经排好的排列中,让A,C不相邻,有方法。由分步计数原理得,共有12×3=36(种)方法。

(3)4个不同的小球放入编号为1,2,3,4的4个盒子中,恰有1个空盒,说明恰有一个盒子中有2个小球,从4个小球中选2 个作为一个元素,同另外2个元素在3个位置全排列,有不同的放法。