求解电荷量的四种方法赏析
■福建省漳州市第三中学 黄辉健
合理运用电流的定义式、电容的定义式、电磁感应定律、欧姆定律,以及动量定理可以求得电荷量这一物理量。下面采用四种方法来求电荷量,供同学们参考。
一、利用电流的定义式和电磁感应定律求电荷量
在电磁感应现象中,求时间t内通过闭合回路的电荷量Q,可以联立公式E=,解得
1.若磁场的磁感应强度B不变,线圈的面积S变化,则求解电荷量的表达式为Q=
2.若线圈的面积S不变,磁场的磁感应强度B变化,则求解电荷量的表达式为Q=
3.若磁场的磁感应强度B与线圈的面积S均变化,则求解电荷量的表达式为Q=
例1如图1所示,虚线MN左侧空间存在垂直于纸面向里的匀强磁场,磁感应强度为B。纸面内有一个圆心角θ=120°的扇形金属线框OCD,半径为r,线框围成的回路电阻为R,顶角O在虚线MN上。当金属线框绕顶角O在纸面内以角速度ω匀速转动时,下列说法中正确的是( )。
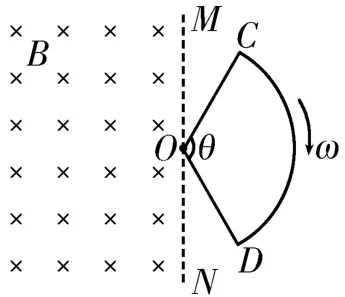
图1
解析:在线框转动一周的过程中,线圈进入磁场的时间,线框中有电流的时间选项A 错误。线框切割磁感线产生的感应电动势,感应电流选项B 错误。线框进入磁场的过程中,通过线框某截面的电荷量,选项C 错误。线框持续转动过程中,线框中电流的有效值满足I2有RT=I2R·,解得I有=,选项D 正确。
规律总结:在电磁感应现象中,因磁通量变化而产生感应电流,求解通过导体某截面的电荷量,则可直接运用公式进行计算。若感应电流是交变电流,则需注意交变电流的峰值、有效值、瞬时值和平均值这四值的区别和联系。
二、利用电容的定义式和欧姆定律求电荷量
电容器的充放电问题涉及电荷量的储存与释放,电容器存储的电荷量由电容器两端的电压决定,电压越大电容器储存的电荷量也越大,计算电容器存储的电荷量的公式为Q=CU,计算电容器存储的电荷量的变化量的公式为ΔQ=CΔU。
例2在如图2所示的电路中,电源的电动势E=10 V,内阻忽略不计,R1、R2、R3、R4均为阻值为20 Ω 的定值电阻,电容器的电容C=30 mF。初始状态下开关S 是断开的,现将开关S闭合,则在闭合开关S 后的较长时间内,通过电阻R4的电荷量是多少?
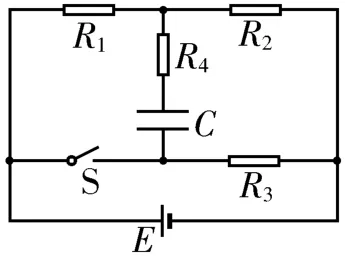
图2
解析:当开关S断开时,电源与电阻R1、R2串联,电阻R3、R4和电容器串联后与R2并联,电容器所在支路可视为断路,因此电阻R3、R4两端的电压为零,电容器两端的电压等于电阻R2两端的电压,且上极板电势较高,带正电,则电容器存储的电荷量Q1==0.15 C。将开关S 闭合后,电阻R1、R2串联后与R3并联,电阻R4和电容器串联后并联在电阻R1两端,电容器两端的电压等于电阻R1两端的电压,且上极板电势较低,带负电,则电容器存储的电荷量Q2==0.15 C。在闭合开关S 后的较长时间内,电容器的正负极发生变化,通过电阻R4的电荷量ΔQ=Q1+Q2=0.3 C。
规律总结:在含电容器的电路中,计算电容器存储的电荷量,需要牢固掌握电路的串、并联关系,熟练运用欧姆定律和电容的定义式。
三、利用动量定理求电荷量
如图3所示,若导体棒沿导轨以速度v做匀速直线运动,则可以联立公式E=BLv,I=,Q=It,求得通过导体棒的电荷量;若导体棒沿导轨做变速直线运动,则可以运用动量定理BILΔt=BLQ=mΔv求得通过导体棒的电荷量
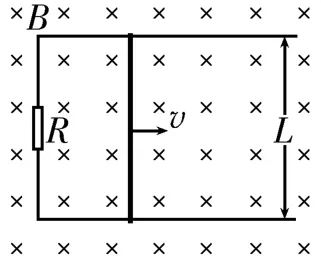
图3
例3如图4所示,两平行金属导轨P1Q1M1和P2Q2M2固定放置,其中P1Q1和P2Q2段为半径r=0.8 m 的四分之一光滑圆弧轨道,O1和O2为对应圆弧轨道的圆心,Q1、Q2在O1、O2正下方且为圆弧轨道和水平轨道的平滑连接点,Q1M1和Q2M2段为足够长的粗糙水平轨道,并处于竖直向上的匀强磁场中,磁感应强度B=1 T,导轨间距L=1 m。两导体棒1、2始终垂直于两导轨且与导轨接触良好,导体棒1、2的质量均为m=1 kg,电阻均为R=1 Ω,导轨电阻不计,导体棒1、2与水平轨道间的动摩擦因数均为μ=0.2。初始时刻,导体棒2静止在水平轨道上,与Q1Q2连线间的距离x1=3 m,导体棒1从与圆心等高的P1P2连线处由静止释放。当导体棒1刚进入磁场时,在导体棒2中点处施加一个与导轨平行且水平向右的恒力F=4 N,经过时间t=0.5 s两导体棒的速度相等。已知导体棒1、2在运动的过程中不会发生碰撞,取重力加速度g=10 m/s2。求:
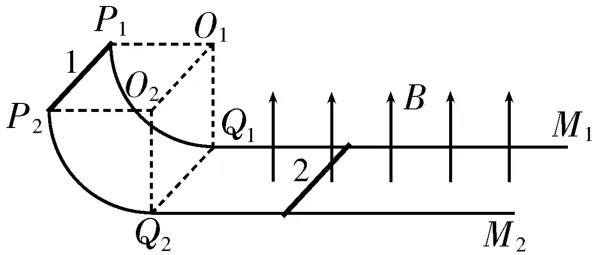
图4
(1)导体棒1 刚到达Q1Q2连线处时对导轨的压力大小。
(2)0~0.5 s时间内通过导体棒2 某截面的电荷量。
解析:(1)导体棒1从P1P2连线处下滑至Q1Q2连线处的过程中,根据动能定理得,解得v0=4 m/s。导体棒1刚到达Q1Q2连线处时,根据牛顿第二定律得根据牛顿第三定律得F压=F支,解得F压=30 N。
(2)导体棒1进入磁场后,由导体棒1、2组成的系统所受合外力等于零,根据动量守恒定律得mv0=2mv1,对导体棒1应用动量定理得--μmgt=mv1-mv0,通过导体棒2某截面的电荷量q=,解得q=1 C。
规律总结:在电磁感应现象中,若研究对象在磁场力的作用下做变速运动,则可以运用动量定理和动量守恒定律求解电荷量。
四、利用平均电流法求电荷量
在电磁感应现象中,闭合电路中产生的感应电流往往是随时间变化的,求解电荷量的关键是计算感应电流的平均值。
1.若闭合电路中产生的感应电流I随时间t呈线性变化,即I=kt+b,则可以利用电流的平均值求解电荷量。
2.若闭合电路中产生的感应电流I随时间t呈非线性关系,当利用I=求得的I是定值时,可以代入公式q=It计算电荷量;当利用I=求得的I是非定值时,则可以利用I-t图像与坐标轴围成的图形面积表示电荷量计算。
例4如图5所示,两足够长的光滑导轨固定在绝缘水平面上,导轨间距最窄处为一狭缝O,以O为原点,水平向右为正方向建立x轴,两导轨与x轴间的夹角均为α=37°,一阻值R=100 Ω 的电阻和电容C=4 000μF的不带电电容器分别与导轨左端相连。x>0的区域内分布着垂直于纸面向内的磁场,磁感应强度大小沿y轴不变,沿x轴的变化满足B=T,0<x≤0.4 m;B=1 T,x>0.4 m。导轨上一金属棒与x轴垂直,在外力F作用下从O点开始以速度v=0.5 m/s向右匀速运动,金属棒在运动过程中与导轨始终保持良好接触,不计金属棒和导轨的电阻,sin 37°=0.6,cos 37°=0.8。求:
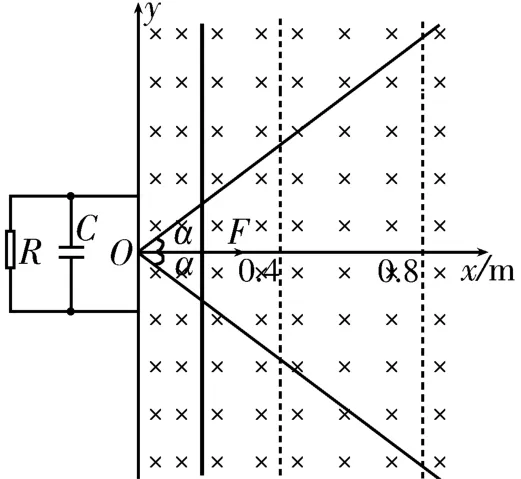
图5
(1)金属棒运动到x1=0.2 m 处时,通过电阻R的电流。
(2)金属棒从x1=0.2 m 处运动到x2=0.8 m 处的过程中,外力F与x的关系。
(3)金属棒从x1=0.2 m 处运动到x2=0.8 m 处的过程中,通过金属棒某截面的电荷量。
解析:(1)金属棒运动到x1=0.2 m 处时,磁感应强度B1=2 T,金属棒的有效切割长度l=0.3 m,则感应电动势E=Blv=0.3 V,感应电流
(2)在0.2 m≤x≤0.4 m 区域内,磁感应强度,有效切割长度则感应电动势E=Blv=0.3 V,感应电流I=3×10-3A,金属棒受到的安培力F安=BIl=1.8×10-3N。在0.4 m<x≤0.8 m区域内,感应电动势,通过电阻的电流,通过电容器的电流1.5×10-3A,金属棒受到的安培力F安=根据平衡条件可知,外力F与x的关系为F=1.8×10-3N,0.2 m≤x≤0.4 m;F=(5x+1)(N),0.4 m<x≤0.8 m。
(3)在0.2 m≤x≤0.4 m 区域内,通过金属棒某截面的电荷量q1=It1=1.2×10-3C。在0.4 m<x≤0.8 m 区域内,通过电阻的电流I1随时间均匀变化,通过电容器的电流I2保持不变,则通过金属棒某截面的电荷量q2=2+I2t2=4.8×10-3C。
规律总结:在0.4 m<x≤0.8 m 区域内,运用电磁感应定律和欧姆定律求得的通过电阻的电流I1随位移x呈正比关系,可以采用平均电流法求解电荷量。
——以2023年高考湖南卷物理第14题为例

