构造『等时圆』 妙解经典题
■河南省新乡市第一中学 宁长兴
“等时圆”模型是以实际生活为依据的真实情景模型,它与日常生活生产联系紧密。以“等时圆”模型为载体的试题,要求同学们在熟练掌握匀变速直线运动规律的基础上,灵活建构“等时圆”模型,实现问题的突破。下面举例分析,供同学们参考。
一、“等时圆”模型的建立
如图1所示,设圆中某一条弦与水平方向之间的夹角为α,圆的直径为d。一质点沿这条光滑弦做初速度为零的匀加速直线运动,根据牛顿第二定律得加速度a=gsinα,根据几何关系得位移s=dsinα,根据匀加速直线运动规律得运动时间,因此所有小球从圆的顶端沿光滑弦轨道由静止下滑到弦轨道与圆的交点或者从圆上的各个位置沿光滑弦轨道由静止下滑到圆的底端所用的时间都相等。
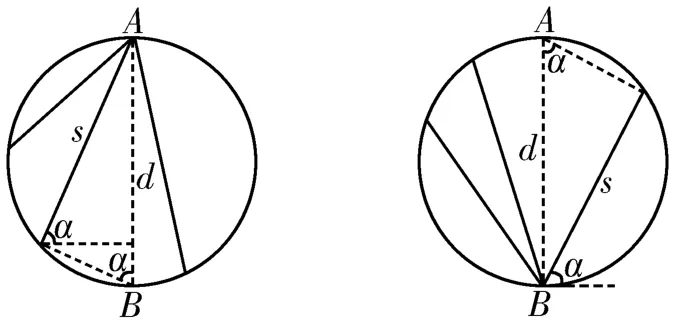
图1
二、利用“等时圆”模型规律求解经典题
例1如图2所示,P为一半径为R的圆周的最低点,光滑细杆PA放在圆周上。在光滑杆上套一个小环,让小环以某一初速度从最低点P抛出沿杆运动,当它抵达A点时,速度恰好为零,求小环沿杆从P点运动到A点所用的时间。

图2
解析:小环沿杆从P点运动到A点做匀减速直线运动,根据运动的对称性可知,小环从P点运动到A点速度减小为零所需的时间与小环从A点由静止下滑到P点所需的时间相等。根据“等时圆”模型的规律可知,小环从A点由静止下滑到P点所需的时间
点评:本题以小环沿光滑细杆上滑为背景,考查匀减速直线运动模型。根据题述情景,将匀变速直线运动模型转化为“等时圆”模型,就可以化腐朽为神奇,快速求得时间。
例2如图3所示,在设计三角形的屋顶时,为了使雨水能尽快地流下,并认为雨水是由静止开始从屋顶上A点无摩擦地流下的。试分析在屋顶宽度(2L)一定的条件下,雨水流下所用时间最短时,雨水离开屋顶时的速率。
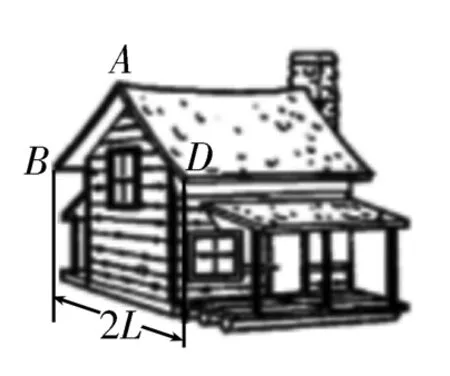
图3
解析:如图4所示,过屋顶上A点作垂线AF与水平线BD垂直,垂足为F,并以L为半径、O为圆心,作与AF、BF相切的圆,转化为“等时圆”模型。根据“等时圆”模型的规律可知,从圆周上各点向最低点B引弦,则雨水从圆周上各点沿弦下滑到最低点B经过的时间相等。从垂线AF引倾角不同的屋顶AB、CB、EB、…,则在不同倾角的屋顶中,只有CB是圆的弦,而其他的均为圆的割线,雨水沿弦CB流下所用的时间最短。根据几何关系可知,弦CB与水平方向之间的夹角为45°,即CF=BF=L。根据机械能守恒定律得,解得雨水离开屋顶时的速率
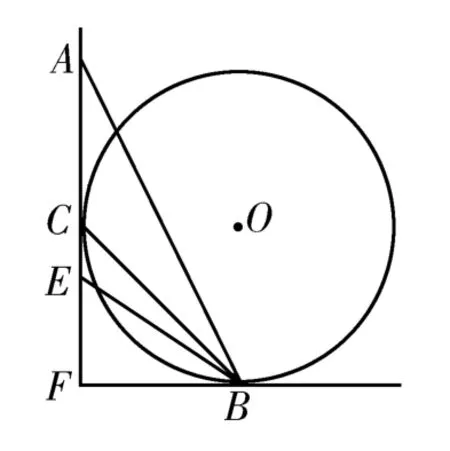
图4
点评:本题以雨水沿屋顶下流为背景,考查匀加速直线运动模型。根据题述情景,实现斜面模型到“等时圆”模型的转化,则可巧妙找到时间最短对应的屋顶倾角。
1.过空间任一点A可作无限多个斜面,若将若干个小物体从A点分别沿倾角各不相同的光滑斜面同时滑下,则在同一时刻这些小物体所在位置构成的面是( )。
A.球面 B.抛物面
C.水平面 D.无法确定
2.如图5所示,位于竖直面内的圆环轨道与水平面相切于M点,与竖直墙相切于A点,竖直墙上另一点B与M点的连线和水平面之间的夹角为60°,C是圆环轨道的圆心。已知在同一时刻,甲、乙两球分别从A、B两点由静止开始沿光滑倾斜直轨道运动到M点,丙球由C点自由下落到M点。则( )。

图5
A.甲球最先到达M点
B.乙球最先到达M点
C.丙球最先到达M点
D.三个球同时到达M点
参考答案:1.A 2.C

