三点共线赛题的多种解法与探究

邓清睿 韩彦昌

(华南师范大学数学科学学院 510631)

1 问题背景

三点共线问题是初高中数学竞赛中的一种常见题型，有直接求证三点共线的，如2020年地中海地区数学奥林匹克赛题第4题[1]；也有在过程中需要说明三点共线的，如用梅涅劳斯定理解答1996年的全国高联题[2]；还有三点共线作为条件带来新结论的，如2022年全国中学生数学奥林匹克竞赛广西预赛的第11题．此类问题的解法常涉及边边关系、边角关系及角角关系的定理和性质．近年来，不少学者提出并探讨相关问题[3]，总结常见的解题方法[4]，但每一道赛题都有其特色，不同的证明方式极大地影响同一道题证明的难易程度．下文将给出2022年“大梦杯”福建省青少年数学水平测试中三点共线问题的三种解法及相关的结论推广．

2 原题呈现与解法

试题(2022年“大梦杯”福建省青少年数学水平测试第12题)如图1，ABCD是平行四边形，∠DAC=45°，以线段AC为直径的圆与AB和AD的延长线分别交于点E和F，过点B作AC的垂线，垂足为H．求证：E,H,F三点共线．

图1

分析 如图1，任意给定一个圆，在旋转不变的意义下取直径AC是唯一的，以AC为一条边作角∠CAF=45°，在翻转不变的意义下也是唯一的．在AF上任取一点D，以AD,CD为邻边的平行四边形ABCD是唯一的，过点B作AC的垂线，垂足H和AB的延长线与圆的交点E也是唯一的．也就是说，点H和点E由动点D唯一确定，随着点D相应地改变．有趣的是，点D的移动导致点H和点E也变动，但E,H,F三点共线的结论不变．特别地，点D与点F重合时，ABCD为圆内接正方形，点H即为圆心，EF为另一条对角线．

证法1如图2，延长BH,AF交于点P，连结FC,PC,FH,HE,CE．要证E,H,F三点共线，只需证∠AHF=∠EHC即可．由AC为直径，BH⊥AC，知∠AEC=∠BHC=90°，那么B,E,C,H四点共圆，所以∠EHC=∠EBC①．由于AD∥BC，则有∠BCA=∠DAC=45°．在△APH中，由于BP⊥AC，则∠APB=45°，所以∠BCA=∠APB，故A,B,C,P四点共圆，因此∠EBC=∠APC②．由AC为直径，得∠PFC=90°，又由于∠PHC=90°，故F,H,C,P四点共圆，则∠APC=∠AHF③．由①②③得∠AHF=∠EHC．

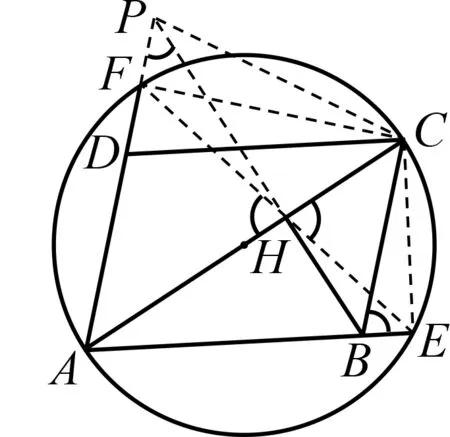
图2

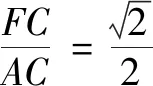
图3

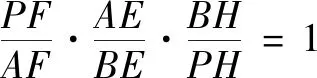
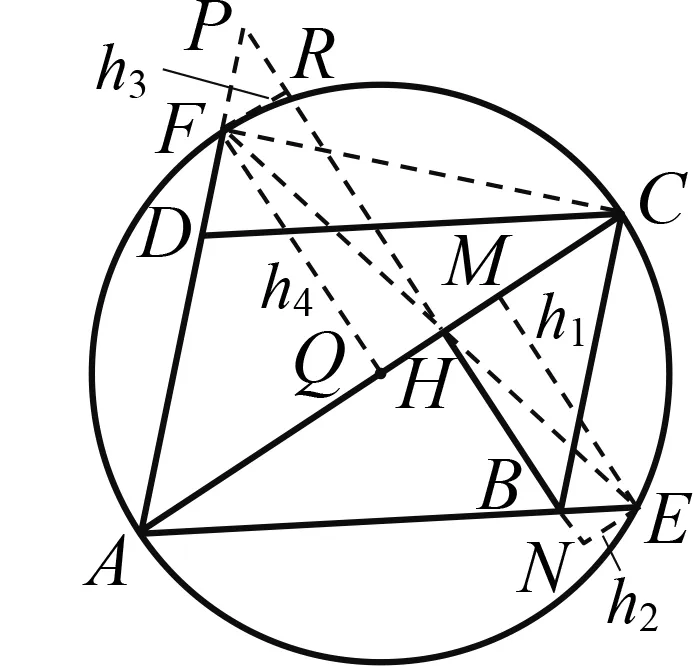
图4

说明本题主要是通过图形中边与边、角与角之间的关系进行转换．证法1直接搭建起角相等的桥梁，步骤较为简洁．证法2主要运用四点共圆与相似三角形的性质，把未知的角关系替换为已知的角关系．证法3运用梅涅劳斯定理的逆定理，虽然能求解，但过程繁琐．

3 结论推广

推论1如图1，ABCD为平行四边形，以长线段AC为直径的圆，与AB和AD的延长线分别交于点E和F，H为线段AC上一点，连结BH，则已知以下任意两个条件可推出余下的一个：① ∠DAC=45°；②BH⊥AC；③E,F,H三点共线．

推论2如图5，ABCD为平行四边形，以长线段AC为直径的圆，与AB和AD的延长线分别交于点E和F，H为线段AC上一点，满足BH⊥AC，连结并延长BH，与DC交于点G，点P在BC上，则已知以下任意两个条件可推出余下的一个：① ∠DAC=45°；②P为BC中点；③F,G,P三点共线．

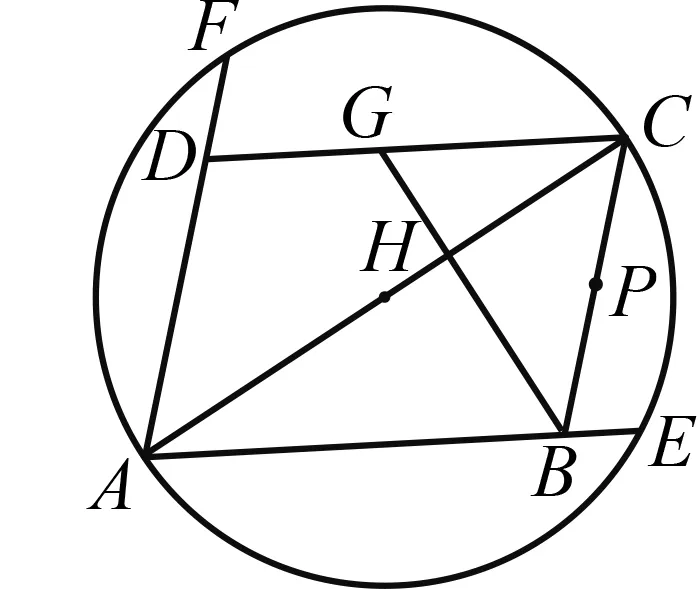
图5

推论3如图6，ABCD为平行四边形，以短线段AC为直径的圆，与AB和AD分别交于点E和F，L为线段AC上一点，连结并延长DL，与AB交于点P，则已知以下任意两个条件可推出余下一个：① ∠BAC=45°； ②DL⊥AC；③E,L,F三点共线．

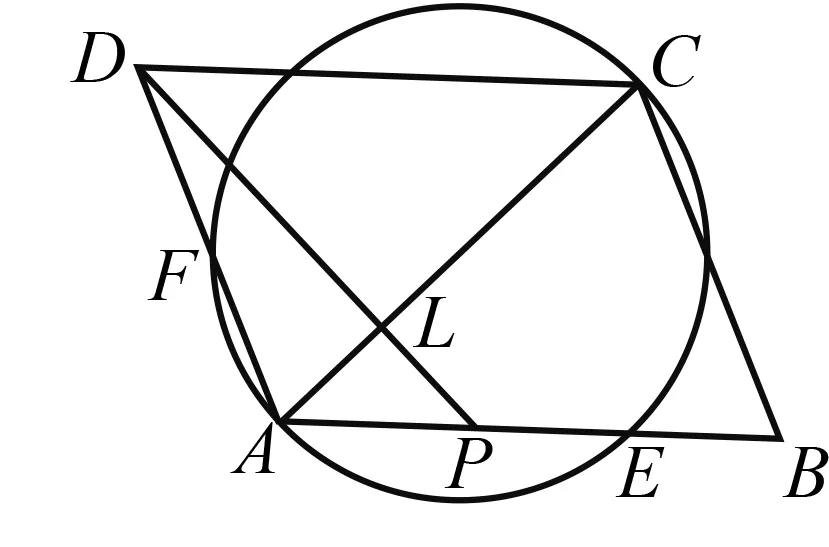
图6

4 推论证明

(1)推论1的证明

已知以下任意两个条件可推出余下的一个： ① ∠DAC=45°；②BH⊥AC；③E,F,H三点共线．前面已证①②⟹③．

①③⟹②：如图3，分别连结FC,CE,FE．要证BH⊥AC，即证∠BHC=90°．由AC为直径，知∠AEC=∠AFC=90°．由①可得∠ACF=45°．显然，A,E,C,F四点共圆，则∠ACF=∠AEF=45°．由于AD∥BC，∠BCA=∠DAC=45°，则有∠BCA=∠AEF，于是B,E,C,H四点共圆，故∠BHC=∠AEC=90°．

②③⟹①：如图3，分别连结FC,CE,FE．显然A,E,C,F四点共圆，则∠DAC=∠CEF④．由AC为直径和②，∠AEC=∠BHC=90°，得B,E,C,H四点共圆，故∠HBC=∠CEF⑤．由AD∥BC，得∠DAC=∠HCB，由④⑤，得∠HBC=∠HCB，由②知△HBC为等腰直角三角形，所以∠DAC=∠HCB=45°．

(2)推论2的证明

已知以下任意两个条件可推出余下的一个： ① ∠DAC=45°；②P为BC中点；③F,G,P三点共线．

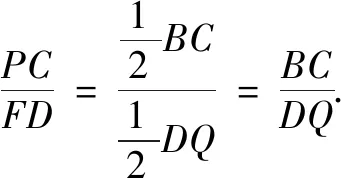
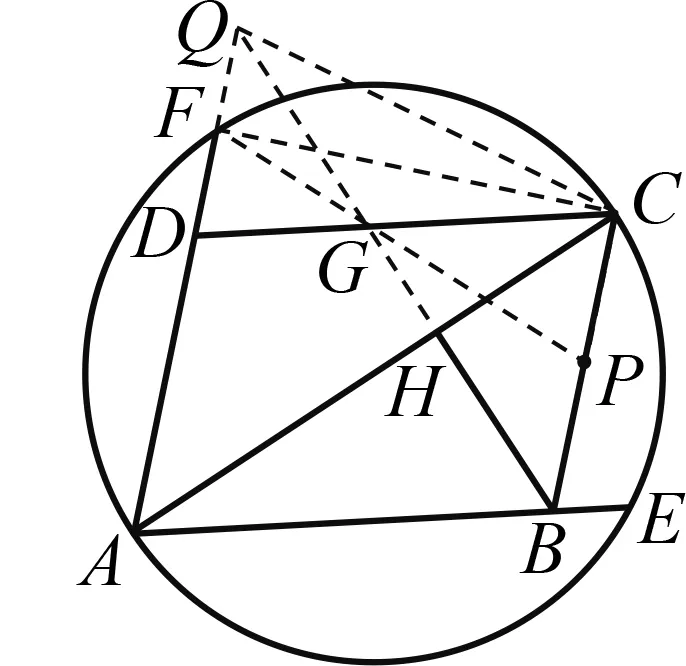
图7

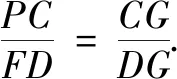
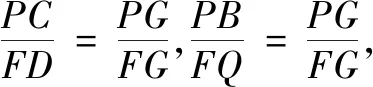
(3)推论3的证明

已知以下任意两个条件可推出余下的一个： ① ∠BAC=45°；②DL⊥AC；③E,L,F三点共线．

①②⟹③：如图8，分别连结FL,EL,FC．要证③，只需证∠CFE=∠CFL．显然A,E,C,F四点共圆，则∠CFE=∠BAC=45° ④．由AC为直径，知∠AFC=90°，故∠DFC=90°．由②知∠DFC=90°=∠DLC，所以D,C,L,F四点共圆，则∠CFL=∠CDL．由AB∥DC，则∠LCD=∠BAC=45°．又∠DLC=90°，则∠CFL=∠CDL=45° ⑤．由④⑤得∠CFE=∠CFL．

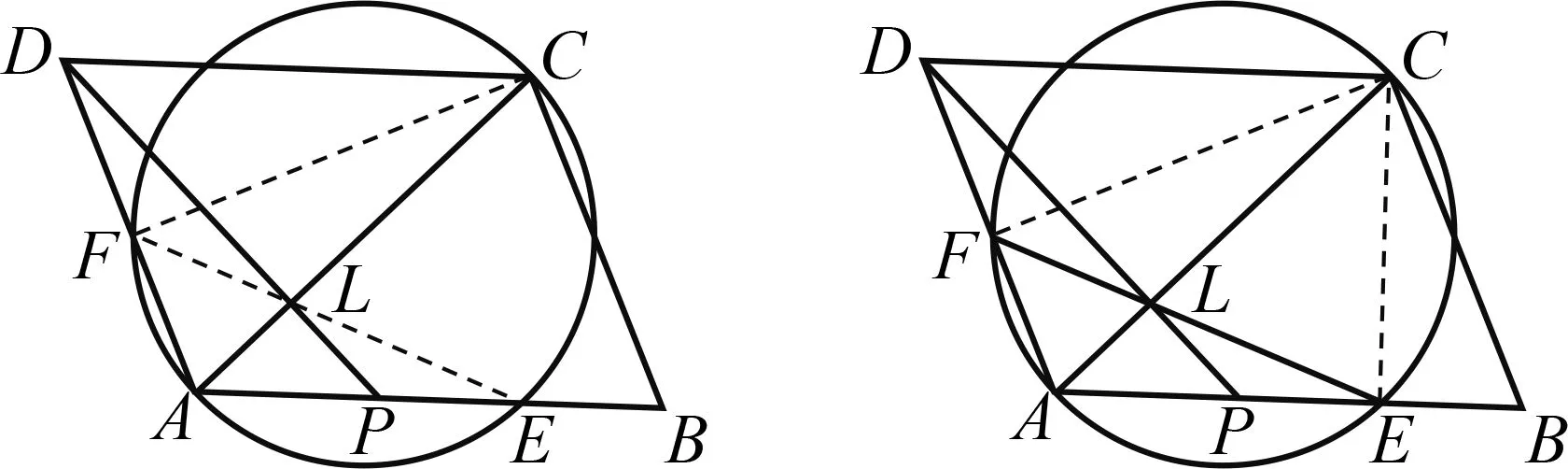
图8 图9

①③⟹②：如图9，连结CE,FC．由AC为直径，知∠AEC=90°，由①知∠ACE=45°．由A,E,C,F四点共圆，知∠AFE=∠ACE=45°．由AB∥DC，得∠ACD=∠BAC=45°，则∠AFE=∠ACD，故D,C,L,F四点共圆，则∠DLC=∠DFC=180°-∠AFC=90°．故②成立．

②③⟹①：如图9，连结CE,FC．由A,E,C,F四点共圆，得∠BAC=∠CFE④．由AC为直径，知∠DFC=180°-∠AFC=90°．由②知∠DLC=∠DFC=90°，所以D,C,L,F四点共圆，则∠CDL=∠CFE⑤．由AB∥DC，知∠APL=∠CDL⑥．由④⑤⑥得∠BAC=∠APL，由②可知，△ALP为等腰直角三角形，所以①成立．