依托TPACK理论，推进统计信息化教学——以“一元线性回归模型的应用”为例*

徐彩凤

(福建省厦门市同安实验中学 361100)

《教育部关于实施全国中小学教师信息技术应用能力提升工程2.0的意见》特别提出信息技术应用能力是新时代高素质教师的核心素养．《普通高中数学课程标准(2017年版2020年修订)》也指出高中数学教学要注重信息技术与数学课程的深度融合，提高教学的实效性[1]．可见，数学教师不仅仅要把适合本学科的信息技术引入课堂，借助信息技术的强大功能提升学生对基础数学知识的理解和掌握，还要鼓励学生动手操作信息技术软件，感受其强大功能，进而加深对数学学科的热爱．为达到信息技术与数学教学的深度融合，教师需要综合考虑信息技术、教学法以及学科内容三者的关系，将它们进行有机融合，这可以联系到整合技术的学科教学法知识(TPACK)理论[2]．

1 TPACK框架简介

TPACK是一套符合信息技术时代教师专业发展需要的专业知识体系，它是由CK(学科知识)、PK(教学法知识)、TK(技术知识)、PCK(学科教学知识)、TCK(整合技术的学科知识)、TPK(整合技术的教学法知识)和TPACK(整合技术的学科教学知识)等七个部分组合而成，各个元素之间的关系如图1[3]．TPACK追求的是在学科教学的过程中，将现代信息技术与学科进行整合．TPACK框架下的数学教学，要求教师应以CK,PK,TK三个核心要素为基础，运用整合技术的数学教学知识(TPACK)进行教学[4]．

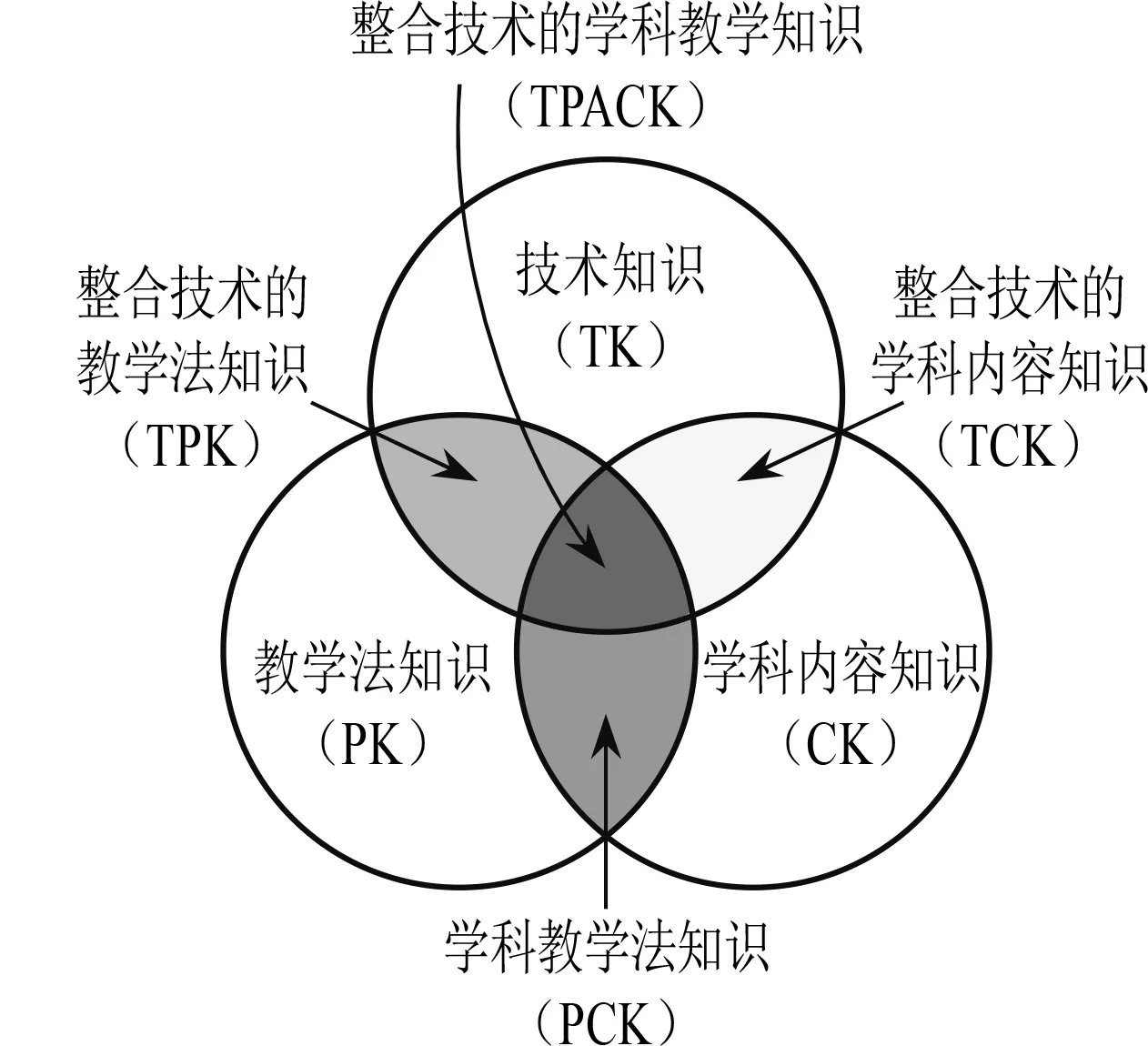
图1

2 TPACK框架下的统计教学

“统计与概率”是高中数学的四大主线之一，用样本估计总体是统计的基本思想，估计和假设检验是两种基本而重要的推断方法．必修课程中的统计主要是关于单变量总体的估计或推断，选修课程中的统计是通过成对数据研究两个随机变量之间的关系．在统计学习中，数据处理、图表绘制是基本能力，列统计表、画各类统计图、复杂的数值计算可以借助Excel、R软件、GeoGebra(下称GGB)等软件快速、准确地解决．真实的统计问题中繁杂的数据整理往往是学生的绊脚石，当学生能借助信息技术这个脚手架来解决问题，就可以深入理解统计概念和方法，思考如何把统计概念和方法用在具体的问题上，及针对具体的问题情境应选择哪个统计量来解决问题．如此，在提高学习效率的同时，学生学习统计和利用统计知识处理具体问题的兴趣必将大大提高．反观高考中的数学统计题，更多考查学生运用统计知识处理问题的能力，而繁杂的计算通常以参考数据形式体现．

在统计教学中，教师先对统计知识(CK)进行分析，确定教学目标，再选择合适的教学法(PK)和信息技术支撑软件(TK)．接着对这三个要素进行整合，运用整合技术的数学知识(TCK)导入新课，激发学生的求知欲；运用学科教学知识(PCK)采用问题式教学和探究式教学，学生以合作探究、实践操作等形式在解决问题的过程中完成对新知的建构和理解；运用整合技术的教学法知识(TPK)提高课堂效率，增强课堂的灵动性(图2)．

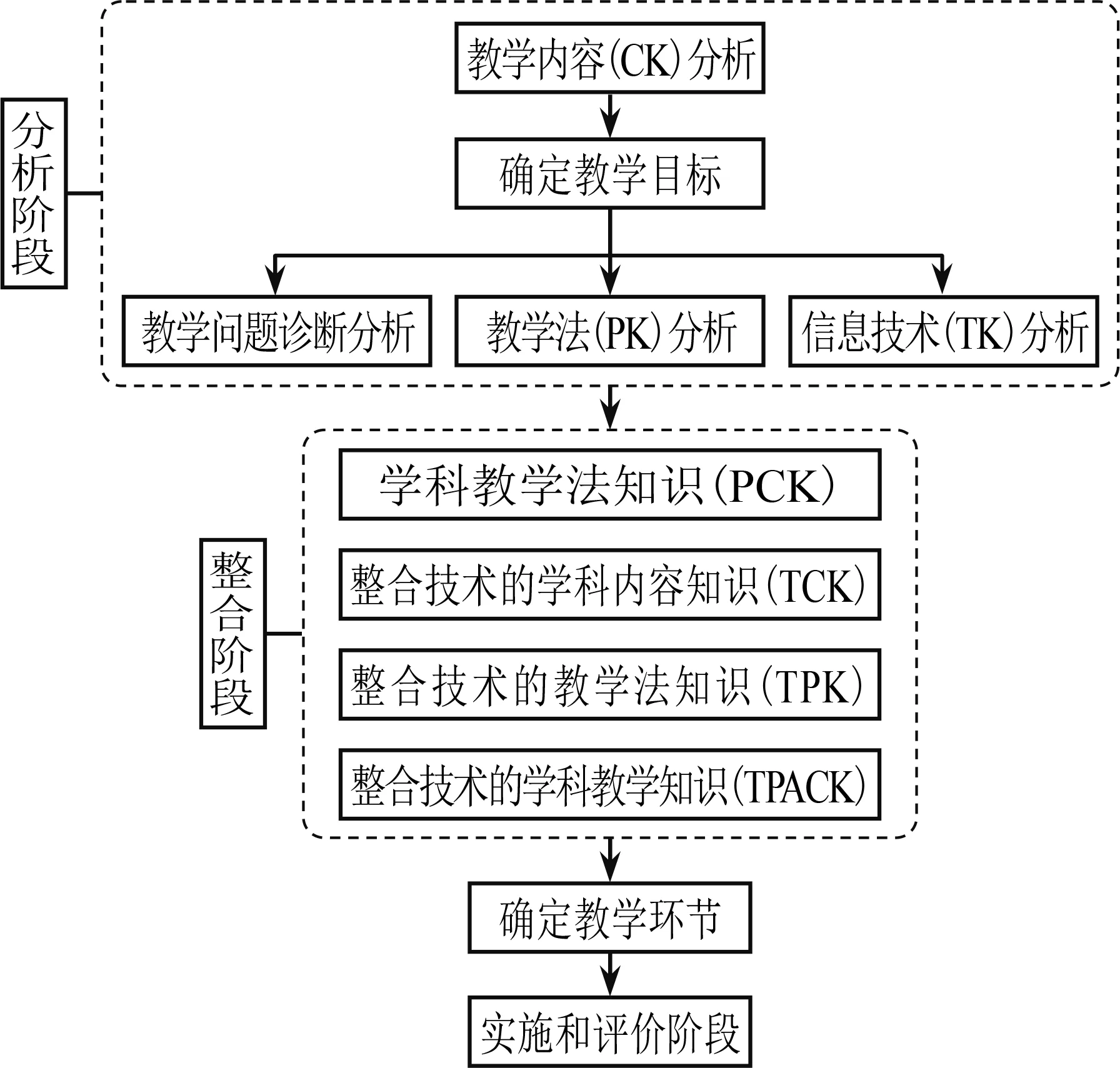
图2

3 基于TPACK框架的信息化教学实践

3.1 课标分析与教学目标

基于以上分析，以人教A版(2019)选修第三册“一元线性回归模型的应用”为例，寻找信息技术与统计教学深度融合的有效途径．该部分的课标要求为“能通过具体实例说明一元线性回归模型修改的依据和方法，会使用相关统计软件．”针对课标要求，结合TPACK理论确定如表1所示的教学目标．

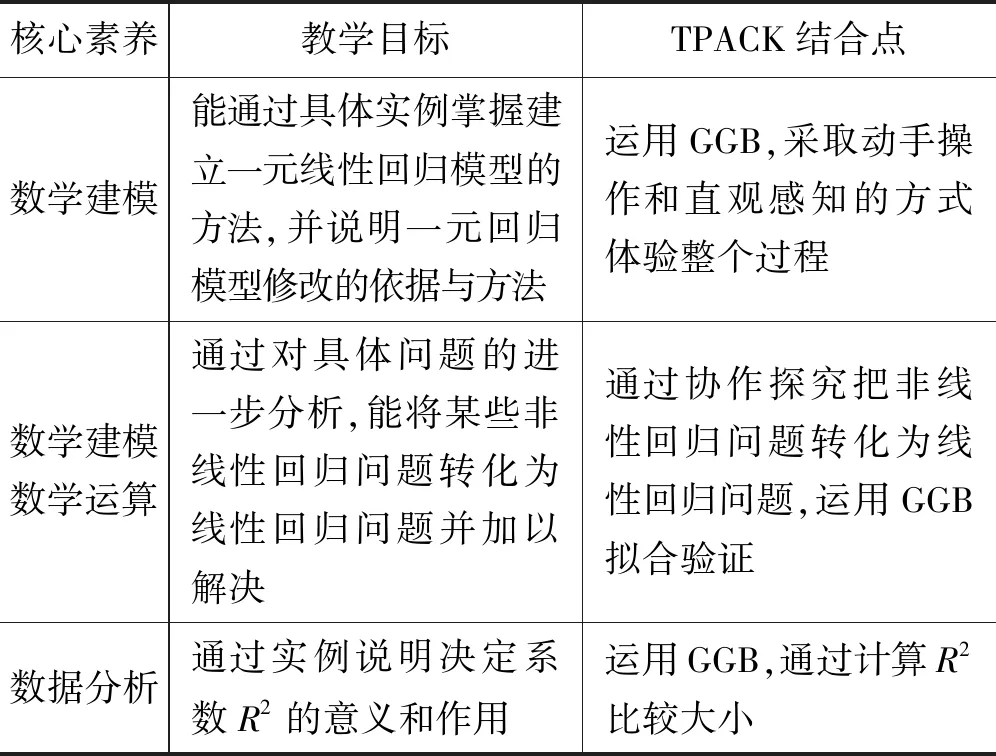
表1 教学目标及TPACK结合点

3.2 教学过程

3.2.1回顾旧知，统一起点

经验表明，对于同一树种，一般而言树的胸径(树的主干在地面以上1.3 m处的直径)越大，树就越高．由于测量树高比测量胸径困难，因此研究人员希望由胸径预测树高．在研究树高与胸径之间的关系时，某林场收集了某种树的一些数据如表2所示，试根据这些数据建立树高关于胸径的经验回归方程．(选自人教A版(2019)选修第三册第113页例)

表2 某种树胸径与树高数据

问题1建立一元线性回归模型的步骤是什么？

追问 回顾上一节课的操作过程，你能利用GGB解决问题吗？请尝试解决．

师生一起回顾建立一元线性回归模型的基本步骤．学生使用GGB自主解决问题得到图3，教师给予适当分析和点评．

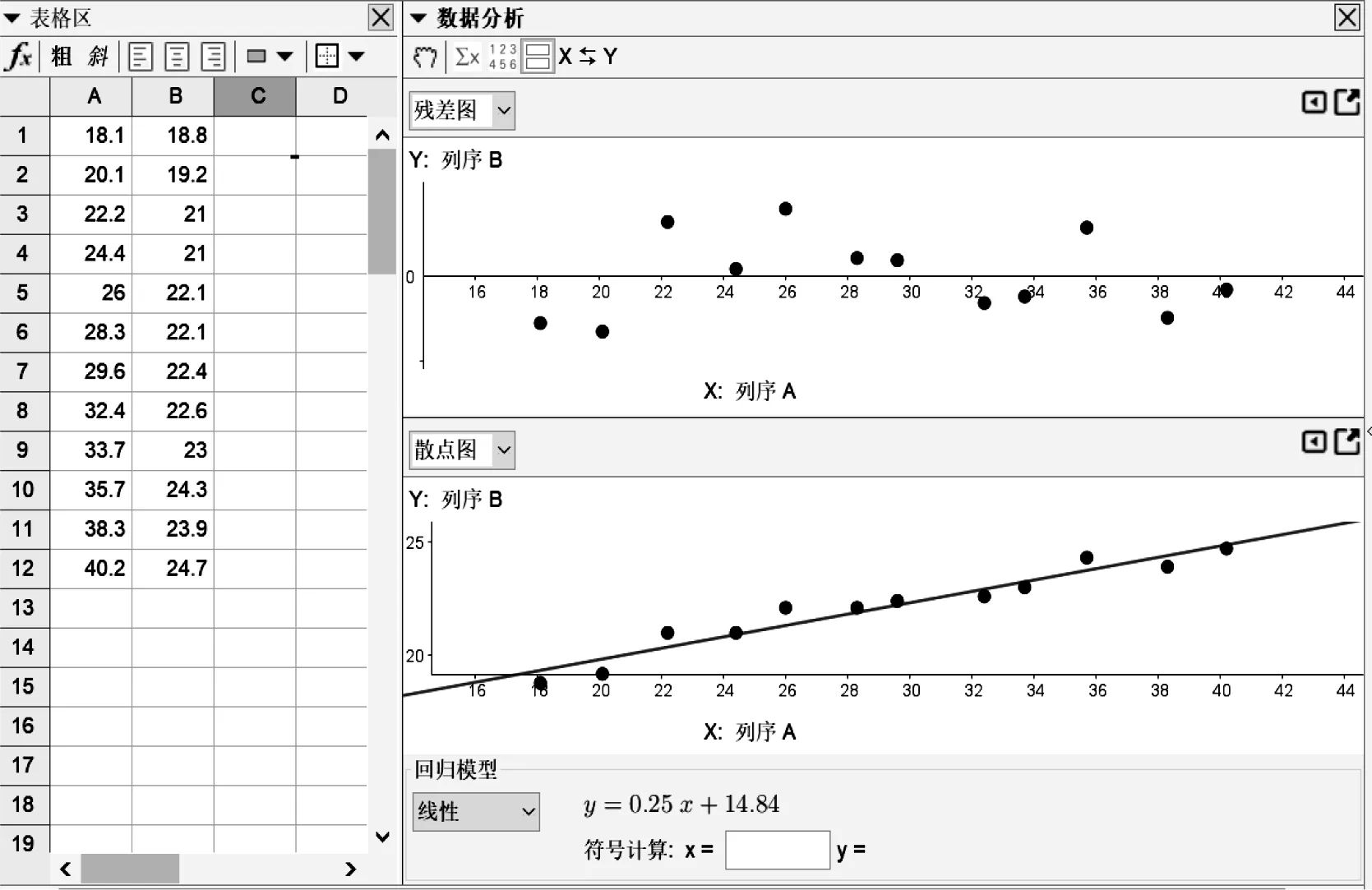
图3

教学思考利用学生的旧知来导入新知是一种知识迁移的策略．美国心理学家奥苏贝尔说过，影响学生新知学习唯一最重要的是——学生已经知道了什么．从课本实例入手，统一学习起点，但由于实际数据的复杂性，若直接用纸笔算，难以进行．有些教师会直接舍去该题，而选择数据易操作的题目，如此便削弱了一元线性回归模型与现实世界之间的关联．本课通过GGB软件的数据分析功能解决该题，同时使学生树立技术应用的意识，以此来培养学生应用新技术的自觉性．

3.2.2问题引领，激发思维

人们常将男子短跑100 m的高水平运动员称为“百米飞人”．表3给出了1968年之前男子短跑100 m世界纪录产生的年份和世界纪录的数据．试依据这些成对数据，建立男子短跑100 m世界纪录y关于纪录产生年份t的经验回归方程．(选自人教A版(2019)选修第三册第115页问题)

表3 100 m世界纪录数据

问题2按照例题中建立一元线性回归模型的方法，你能利用GGB解决吗？

追问1 画散点图，计算样本相关系数，并判断能否用一元线性回归模型拟合？若可以，请建立对应的经验回归方程；若不可以，请说明理由．

学生利用GGB作散点图，散点看上去大致分布在一条直线附近，指导学生点击GGB数据分析中的∑x按钮，可得样本相关系数为-0.855 9，可以推断男子短跑100 m世界纪录与纪录产生年份两个变量负线性相关，用一元线性回归模型建立经验回归方程．

追问2 观察到年份t比较大，能否用模型y=c1+c2(t-1 895)来拟合呢？

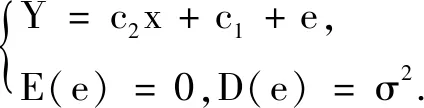
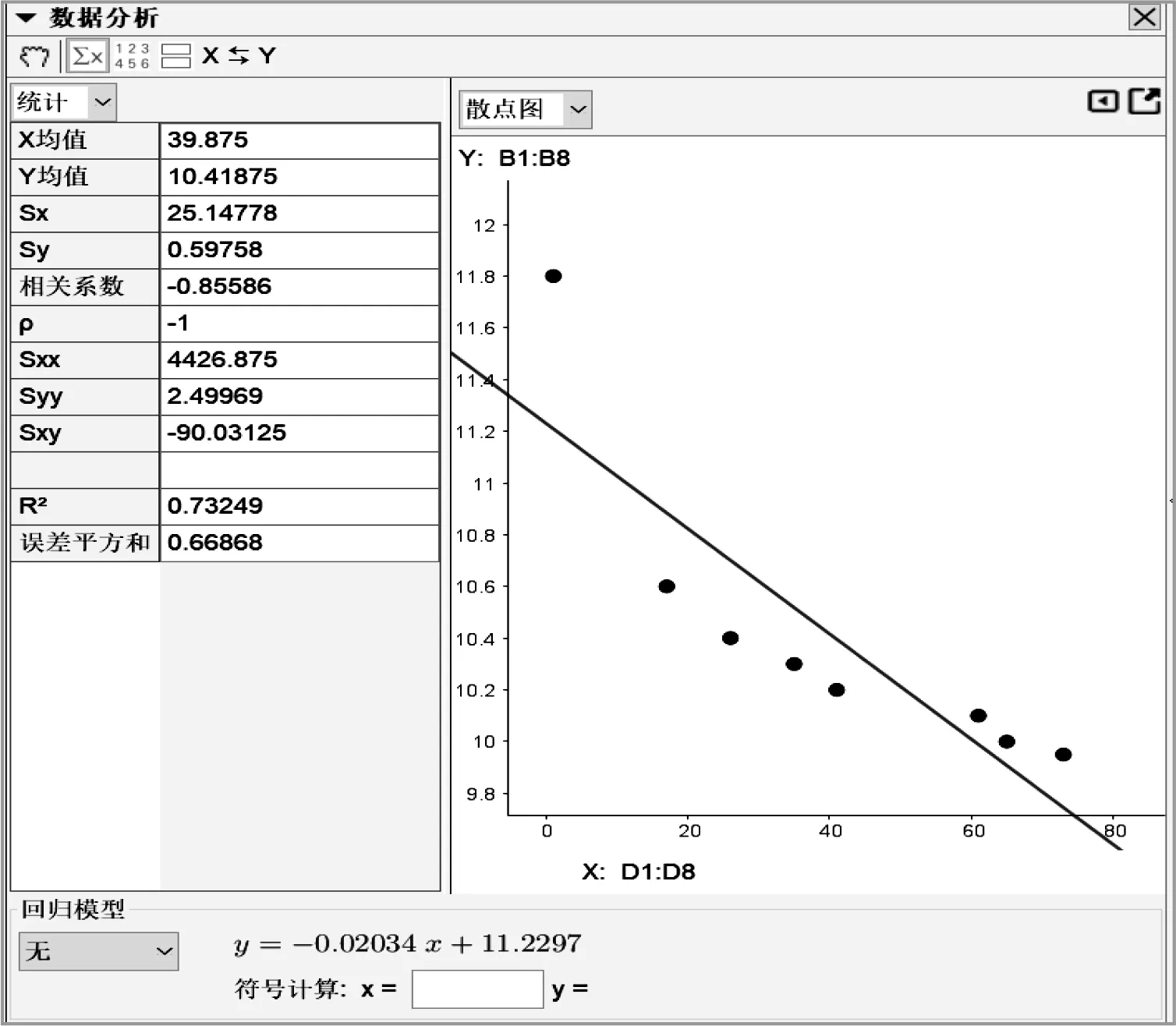
图4

学生得出结论：成对样本数据呈现出明显的非线性相关的特征．

追问4 你能对模型进行修改，以使其更好地反映散点的分布特征吗？

引导学生观察散点图，回顾已有的函数知识，选择合适的函数模型．

学生讨论得到以下模型：(1)y=c1+c2ln(t- 1 895)(c2<0)；(2)y=c1ec2(t-1 895)(c1>0,c2<0)；(3)y=c1(t-1 895)c2(c1>0,c2<0)．

教学思考数学教学应结合教学任务及其蕴含的数学学科核心素养设计合适的情境和问题，引导学生用数学的眼光来探究真实问题背后的数学知识[1]．本课以男子短跑100 m世界纪录为情境，利用GGB的作图功能发现第一点偏差较大，提出问题：你能对模型进行修改，以使其更好地反映散点的分布特征吗？引导学生思考问题背后的数学知识：选择合适的函数模型．通过整合信息技术与课程教学，学生在此过程中体会数学知识的发生、发展过程，理解数学内容的本质．

3.2.3实验探究，亲历建构

问题3观察以上3个式子的结构，你能通过变量变换将上述非线性回归模型化为一元线性回归模型，从而得到求解吗？

教师引导学生观察以上3个模型中式子的结构，分组交流操作得到：

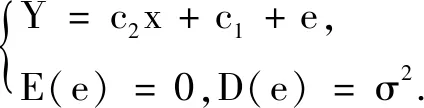
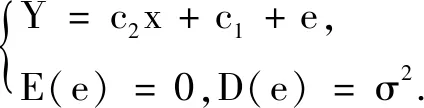
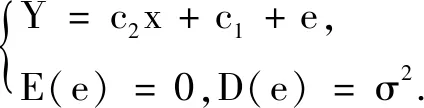
追问1 你能用GGB建立以上3种经验回归方程吗？

学生通过协作探究，利用GGB得到(图略)．

追问2 你能写出以上3种经验回归方程吗？

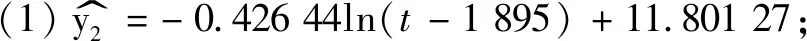
问题4以上我们共建立了男子短跑100 m世界纪录关于纪录产生年份的4个经验回归方程，你能判断哪种经验回归方程具有更好的拟合效果吗？

生：可利用直接观察法和残差分析．

接着教师引出与残差平方和相关的统计量决定系数R2，用R2比较4个回归方程拟合的效果，并说明R2的意义．(用GGB计算)

教学思考数学实验是为了探索数学知识、检验数学结论、形成假设而进行的某种操作或思维活动，是学生通过观察、操作、实验等实践活动来进行数学学习的一种方式．[5]教学中，教师提供恰当的平台和技术指导，学生通过探究交流、操作验证得到四种经验回归方程，再恰当引出决定系数R2，利用R2判断模型的拟合效果．信息技术与数学课程整合体现了“做中学”理念，是积累基本活动经验的重要途径．

3.2.4归纳总结，思维可视

借助希沃白板上的思维导图功能(图5)和学生一起归纳反思本节课的知识和方法．

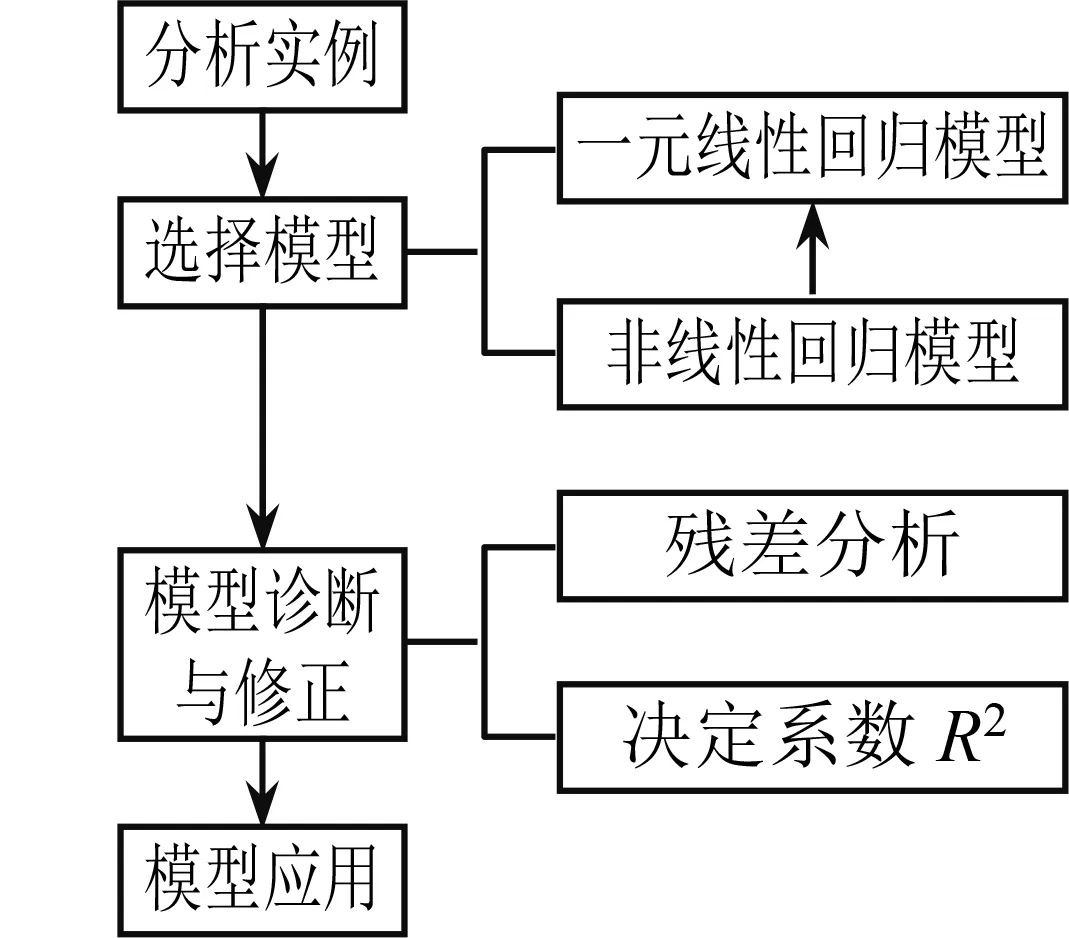
图5

教学思考数学思维导图通过框架的确立向四周延伸，能够有助于学习者建构良好知识体系，优化课堂总结．[6]希沃白板的思维导图可边教学边绘制，逐渐形成一个思维的网络，让数学思维可视化．同时提高学生的课堂参与度，帮助学生在系统化的数学思维过程中建构完整的数学知识体系．

4 TPACK理论在信息化教学中的作用

4.1 要素分析，整合教学

CK,PK,TK是TPACK的三个核心要素，这三个要素的整合具有递进关系(图6)．

图6

在此过程中，主要考虑利用信息技术呈现知识的效果以及与教学方法的适应程度，将信息技术以各种形式融入教学各要素中，以取得最优化的教学效果．

4.2 技术融合，深度教学

基于TPACK框架进行信息技术与数学教学融合，于教师来说，关注的不仅仅是信息技术本身，而是信息技术与数学基本知识和方法的契合点．这就要求教师在设计一堂课之前能围绕“什么技术可以促进教学，如何把技术融合到数学知识和教学法当中”展开思考，针对重难点选择恰当的技术手段辅助突破．对学生而言，一方面信息技术的有效使用提高了课堂效率，激发了学生的学习兴趣；另一方面学生通过结合数学知识亲自操作信息技术，感受到其带来的巨大力量，探索单纯用纸笔难以解决的问题，增强了学生的求知欲和探索欲，同时培养学生观察、探究和解决问题的能力，以期真正实现信息技术与数学教学的深度融合．