空间冗余索驱动并联机构的耦合振动特性研究

于金山， 陶建国， 王国星， 李 潇， 王浩威

(1. 哈尔滨工业大学 机电工程学院， 哈尔滨 150001； 2. 北京卫星制造厂有限公司， 北京 100094；3. 北京空间飞行器总体设计部， 北京 100094)

随着航天技术的发展，未来的深空探测、天文观测等工程对空间结构(如空间天线、大型 SAR卫星等)的尺寸提出了更大的要求。受运载火箭运载能力的限制，目前可发射入轨的航天器的尺寸难以满足大型空间结构的尺寸要求，因此，需要采用在轨装配[1]的方式对大型空间结构进行在轨构建，从而突破功能的限制，解决大型空间结构的建造问题。考虑到航天员出舱进行装配作业具有很大的危险性，并且难以满足长时间的工作任务要求[2]，因此需要通过操控机器人或机械臂的方式进行无人在轨装配。

杆支撑串联式机械臂是目前执行空间操作任务的主要装备[3]，其特点是控制方便，但质量较大，运动时具有较高的能耗。此外，当臂杆较长时，机构的刚度会降低。而绳索作为一种柔性体，具有结构简单、质量轻、承载能力强等特点，很容易进行大跨度的构建，因此在航天领域具有大范围工作空间要求的环境得到了广泛的应用(如用于在轨服务的空间绳系机器人[4]以及用于空间抓捕作业的绳索捕获机构[5]等)。本文针对大型空间结构的在轨装配问题，提出了索并联机构的方案，即通过驱动多根绳索牵引执行器进行在轨装配作业，其结合了绳索驱动的优势和并联机构的特性，具有结构简单、易于构建、质量轻、负载/质量比大[6]等特点，十分契合大范围、高速度的在轨装配要求，因此在该领域具有良好的应用前景。

由于绳索相对于刚性杆支撑结构具有较低的刚度，因此索并联机构在工作过程中易产生振动，从而影响机构的稳定性和定位精度。由于大跨度索并联机构具有低刚度和低阻尼的特性，因此在运动过程中更容易产生振动，且该振动如果不予以控制的话，很难在短时间内消除。因此，开展机构的振动特性研究可以得到机构的振动规律，研究结果对于抑振方法的选择以及控制器的设计具有指导意义。Diao等[7]针对绳索在外界激励下，不仅会产生轴向振动，也会产生横向振动这一问题，分析了绳索的横向振动，并得出了绳索的横向振动相对于其轴向振动对机构的影响可以忽略这一结论。Du等[8]考虑了绳索的动力学特性，将其分为有限的单元，建立了一种大跨度索并联机构的动力学模型，并在此基础上仿真分析了绳索的振动对机构的定位精度的影响，但没有对机构的振动机理进行深入地研究。Weber等[9]对一种平面索并联机构的振动问题进行了研究，针对末端执行器在转动方向的易产生振动的问题，采用了引入反作用轮的方法进行抑振，该方法对于抑制末端执行器在转动方向的振动具有良好的效果。Jamshidifar等[10]为了降低一种冗余约束的索并联机构的振动，把机构刚度最大化这一条件引入了控制策略。仿真结果表明所设计的控制器具有较高的鲁棒性。Schmidt等[11]对一种平面索并联机构的稳定性进行了试验研究，试验结果表明通过提高绳索的拉力可以增大机构的刚度，从而降低机构在受到干扰时产生的振动。Heo等[12]为了提高一种八索并联机构的稳定性，提出了一种基于频率的变约束方法，通过调节绳索的张力来改善机构的刚度，从而提高机构的固有频率。但该研究只分析了绳索的振动频率，没有考虑运动平台的振动特性，因此具有一定的局限性。刘志华等[13]利用Newton-Euler方法建立了一种6自由度索并联机构的动力学模型，对其线性化后得到系统的振动方程，进而得出各阶固有频率的分布情况，最后通过绳索受力频谱分析试验对理论计算值进行了验证。但该研究没有分析运动平台的位姿对振动特性的影响。彭苗娇等[14]研究了应用于风洞试验的飞行器模型支撑的索并联机构牵引绳与模型之间振动的耦合关系，为机构的运动控制补偿提供了参考。但该研究只考虑了模型处于中心位置时的工况，缺乏一定的普遍性。吴太欢等[15]研究了绳系结构和绳索预紧力对全模颤振双索悬挂系统刚体模态频率的影响，研究发现，控制悬索预紧力的大小以及合理设计机身上滑轮安装位置可以有效改变双索悬挂系统刚体的模态频率，从而模拟颤振试验的动力学性能。但该研究只考虑了不同振动方向解耦时的振动特性，而没有考虑不同方向耦合情况的振动。

以上研究中，有些研究在分析索并联机构的振动特性时，只考虑了绳索的振动，没有分析运动平台的振动，无法完整地体现系统特性。还有一些研究只考虑了机构在某一特定工况时的振动特性，尤其是运动平台处于中心位置时的振动特性，没有研究运动平台的位置变化对振动特性的影响。本文对一种空间冗余索并联机构的振动特性进行了研究。分析了运动平台的位置以及绳索拉力水平对机构振动特性的影响，并通过仿真和试验研究了不同工况下机构的振动规律。研究结果对于索并联机构的振动控制具有指导意义。

1 机构描述

面向在轨装配的空间索并联机构主要由框架、驱动单元、绳索以及运动平台组成(如图1所示)。驱动单元包含电机、减速器、卷轴、拉力传感器、滑轮等，用于驱动绳索、检测张力等。模块化的驱动单元通过接口与空间大型机械进行对接，从而实现驱动单元的固定及通信。运动平台上面搭载各种适配器，用于执行各种装配作业。整体系统具有结构简单、搭建方便、质量轻、工作空间大、承载能力强、便于维护等特点。

图1 空间冗余索并联机构示意图Fig.1 Schematic diagram of spatial redundant CDPM

本文所设计的索并联机构预期安装在一长方体空间区域，运动平台形状可简化为长方体，其尺寸参数如表1所示。运动平台需要承受3个平动自由度方向的力以及3个转动自由度方向的力矩。由于绳索的单向受力性，索并联机构必须采用冗余驱动的方式，即绳索数量大于运动平台的自由度数[16]。考虑机构布局的对称性，选取绳索数量为8，绳索采用上下交叉布局的方式，框架上部的四个出绳点通过绳索与运动平台底部的四个顶点相连(如图2所示)。为了避免绳索发生干涉，运动平台上部的四个绳索连接点向中间移动一段距离。这种绳索布局方式可以使机构具有较大的承载能力[17]。

表1 索并联机构几何参数Tab.1 Geometric parameters of cable-driven parallel mechanism

由于在空间环境中，绳索不会产生因重力导致的悬链线变形，因此可以将其建模为直线。图2中，OXYZ为全局坐标系，Pxyz为局部坐标系。点P为局部坐标系原点。Bi和Pi(i=1,2,…,8)分别表示出绳点和运动平台连接点。Obi为出绳点在全局坐标系中的位置矢量，Op为局部坐标系原点在全局坐标系中的位置矢量，pi为绳索与运动平台连接点在局部坐标系中的位置矢量，ORP为局部坐标系到全局坐标系的旋转矩阵。

图2 索并联机构构型示意图Fig.2 Schematic diagram of the CDPM conFiguration

单位绳索方向矢量可以表示为

(1)

对索并联机构进行受力分析，ti=tiui(i=1,2,…,8)表示为绳索拉力矢量，ti为绳索拉力值，fp和τp分别为作用在运动平台上的除绳索拉力外的其它合力和合力矩。由力平衡条件可得

(2)

(3)

式(2)和式(3)可合并为

JTT+F=0

(4)

式(4)即为索并联机构的力旋量平衡方程。

2 空间冗余索并联机构振动模型

2.1 刚度矩阵

运动平台在受到微小外力旋量dF时，必然会产生微小位姿变化dX。因此索并联机构的刚度可表示为

(5)

式中，K称为索并联机构的刚度矩阵。把式(4)代入式(5)，得

(6)

由式(6)可以看出刚度矩阵K由两部分组成，前者与绳索拉力有关，称为主动刚度Ka，后者与索并联机构的位姿以及绳索刚度有关，称为被动刚度Kp[18]。对Ka进行计算

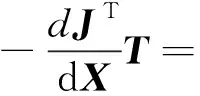
(7)

(8)

索并联机构的雅可比矩阵为

(9)

其与索并联机构的结构矩阵JT互为转置。

把式(9)代入式(8)，得

(10)

设ki为绳索i的刚度，

(11)

式中：Ei为绳索i的弹性模量；Ai为绳索i的截面面积；loi为绳索i的初始长度。因此式(10)中，

(12)

把式(12)代入式(10)，

(13)

于是得到索并联机构的完整刚度矩阵：

(14)

2.2 索并联机构的振动模型

对于本文所研究的索并联机构，虽然绳索的跨度较大，但其质量远远低于运动平台的质量，此外，由于空间不存在空气阻尼作用，且绳索本身的阻尼也很小，因此建模时忽略绳索的质量和阻尼。基于这两个前提，建立索并联机构的自由振动模型

(15)

式中，M为运动平台的质量矩阵。

对于运动平台在平衡位置处的自由振动，系统的固有角频率ω和模态矢量q的关系可以表示为

(K-ω2M)q=0

(16)

(17)

3 振动特性仿真

3.1 理论计算

由式(17)可知，在运动平台的质量确定的情况下，索并联机构的振动特性取决于刚度矩阵K。通过2.1节的分析可以发现，刚度矩阵K与索并联机构的位姿以及绳索拉力有关。本节通过仿真的方式对索并联机构在不同位置以及不同绳索拉力的条件时的振动特性进行研究，从而分析不同工况时机构的性能。

首先对运动平台处于中心位置时(Op1=[0，0，12.5]Tm)机构的振动特性进行分析。本研究采用密度低且弹性模量大的Dyneema绳索，单位长度的绳索刚度为7.56×105N/m。设定绳索拉力分别为：T=[512.5, 518, 512.5, 518, 517.3，509.7，517.3，509.7]TN，求得主动刚度Ka和被动刚度Kp分别为

刚度矩阵

可以看出刚度矩阵K具有明显的对角线特性，非对角线元素接近0。因此，运动平台处于中心位置处时，不同方向的刚度是解耦的。通过刚度矩阵还可看出机构在x方向和y方向的平动刚度以及绕x轴(α方向)的转动刚度较大，而在z方向的平动刚度以及绕y轴(β方向)和z轴(γ方向)的转动刚度相对较小。

机构的各阶固有频率和对应的模态矢量如表2所示。由于不同方向的刚度是解耦的，因此机构的模态也呈现出相互独立的特点。由于索并联机构的跨度以及运动平台的质量都较大，因此机构的各阶固有频率较低。z方向的固有频率最低，为2.28 Hz，α方向和β方向的固有频率较高，分别为6.97 Hz和7.74 Hz。

表2 中心位置处索并联机构的各阶固有频率和模态矢量Tab.2 The natural frequencies and modal vectors of the CDPM at the center position

在运动平台处于边缘位置时(Op2=[20，18,5]Tm)，设定绳索拉力矩阵T=[810.4, 365.1, 57.1, 534.6, 476.0, 164.0, 51.1, 132.6]TN，机构的主动刚度和被动刚度分别为

Ka=

Kp=

刚度矩阵

K=

此时矩阵的非对角线元素增大，不同方向的刚度呈现出强耦合性。机构的各阶固有频率和模态矢量如表3所示。由于不同方向刚度的耦合性，机构的模态也表现出强耦合特点。对于固有频率最低的两个模态，一阶固有频率对应的模态矢量主要为x方向、y方向以及α方向的耦合。二阶固有频率对应的模态矢量接近z方向。除了第5阶模态矢量，其余各阶模态矢量均为6个方向的耦合。因此，当运动平台远离中心位置时，由于不同方向的刚度并不相互独立，其振动特性相对复杂。

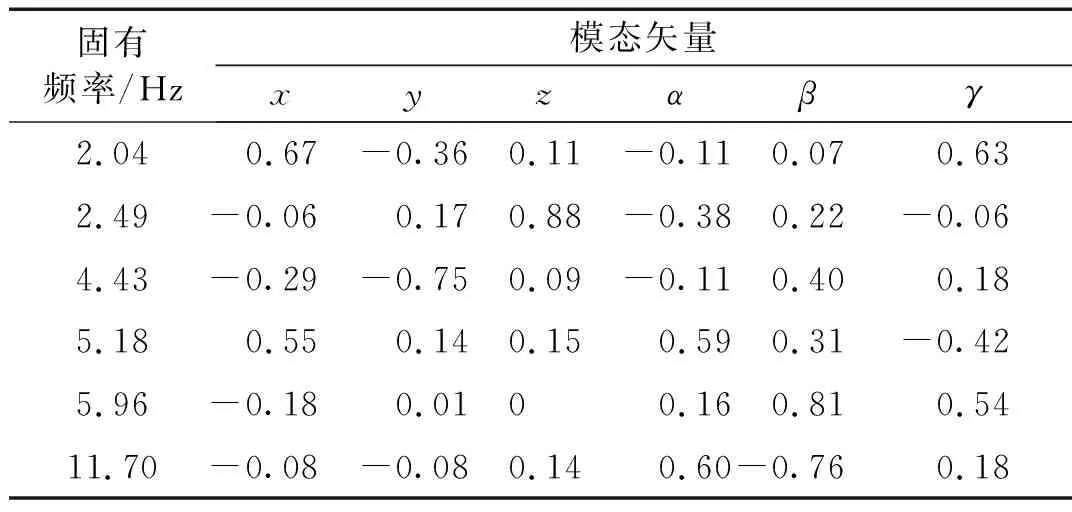
表3 边缘位置处索并联机构的各阶固有频率和模态矢量Tab.3 The natural frequencies and modal vectors of the CDPM at the the edge position

(a) 中心位置

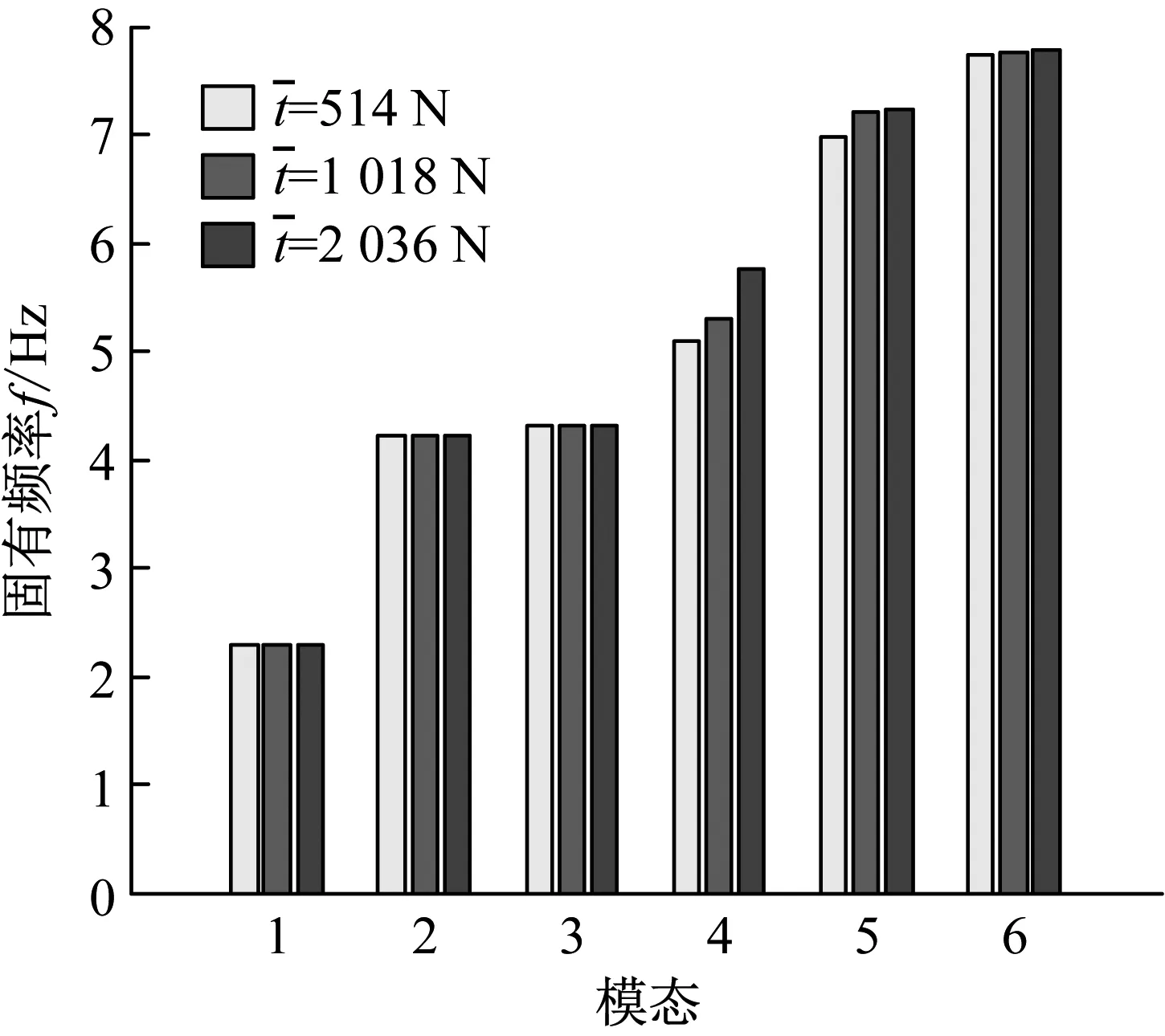
(b) 边缘位置图3 绳索拉力水平对机构固有频率的影响Fig.3 Influence of rope tension level on the natural frequency of the mechanism

从图中可以看出，当运动平台处于中心位置处时，提高绳索拉力水平对于增加机构的固有频率具有一定的效果，尤其是对于机构的4阶模态和5阶模态下的固有频率，但该效果并不明显。而当运动平台处于边缘位置处时，提高绳索拉力对于增加机构的固有频率几乎没有影响。这是因为本文所研究的索并联机构所采用的绳索具有较大的弹性模量，机构的被动刚度较大，此时通过增大绳索拉力来提高主动刚度的方式对于整体刚度的提高的效果很小。整体来看，运动平台的位置对机构的模态影响较大，不仅各阶固有频率会发生变化，与之相对应的模态方向也会发生改变，表现为不同方向之间较强的耦合性。

3.2 仿真试验

为了验证上述模型建立的正确性，并深入分析索并联机构的振动特性，本节在ADAMS环境中建立了空间索并联机构的模型(如图4所示)。该模型包括滑轮、绳索及运动平台。将运动平台的位置分别设定为中心位置(Op1=[0，0，12.5]Tm)和边缘位置(Op2=[20，18,5]Tm)，相应的绳索拉力分别与3.1节的理论值相同。设置仿真步长为100，为对运动平台施加不同方向的激励，得到运动平台不同振动方向的时域信号。采用快速傅里叶变换(FFT)将时频信号转化为频域信号，如图5～图8所示。

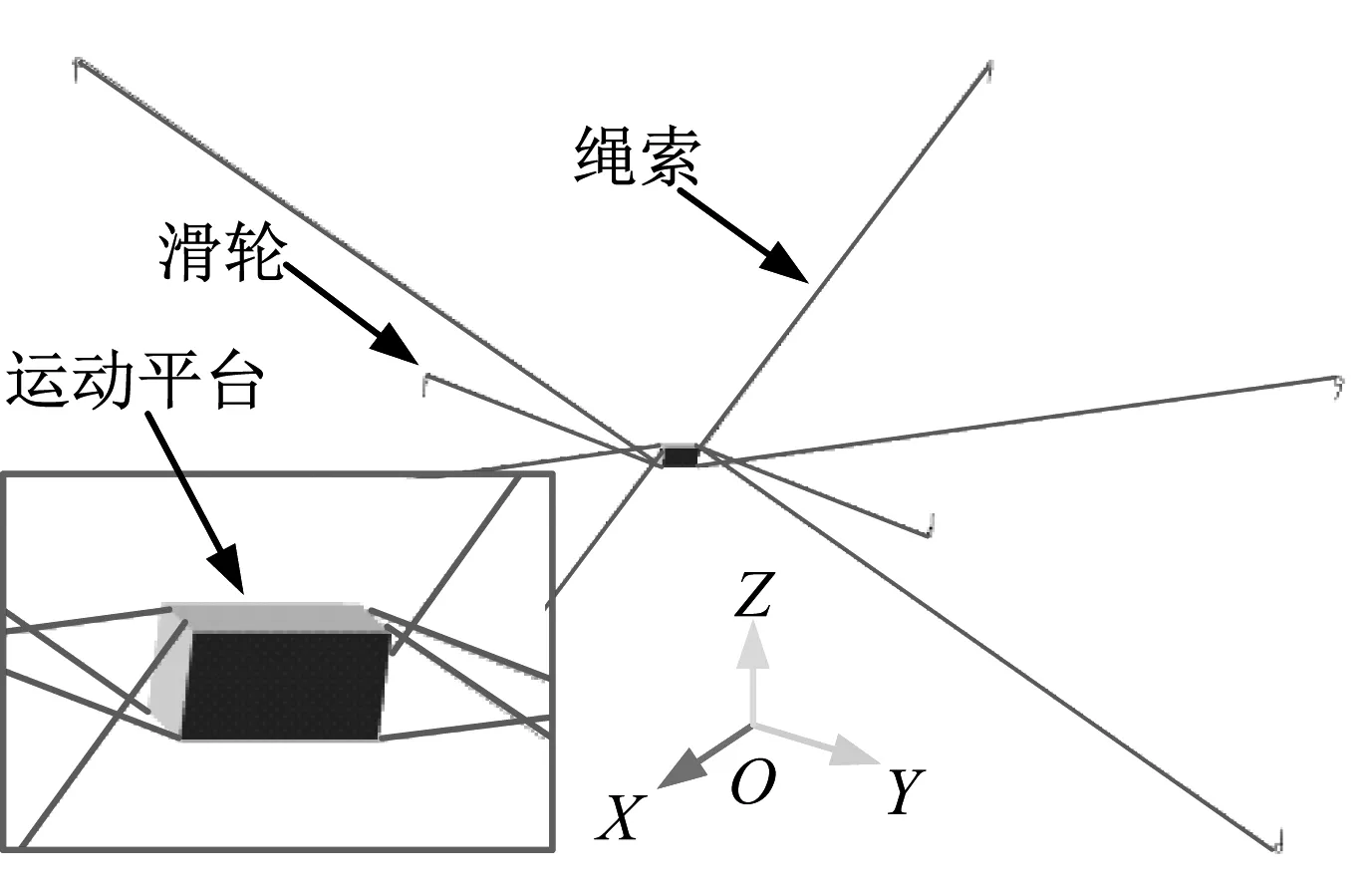
图4 ADAMS中索驱动并联机构的模型Fig.4 Model of cable-driven parallel mechanism in ADAMS

(a) 时域信号

(b) 频域信号图5 中心位置处运动平台的时域信号与频域信号(施加y向激励)Fig.5 Time domain signal and frequency domain signal of the moving platform at the center position (applying y-direction excitation)

(a) 时域信号

(b) 频域信号图6 中心位置处运动平台的时域信号与频域信号(施加z向激励)Fig.6 Time domain signal and frequency domain signal of the moving platform at the center position(applying z-direction excitation)

(a) 时域信号

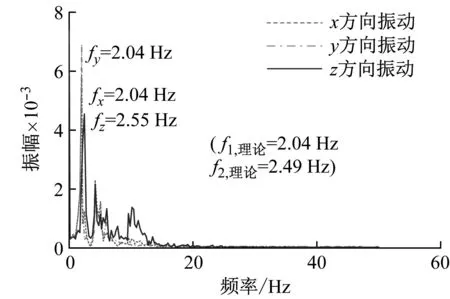
(b) 频域信号图7 边缘位置处运动平台的时域信号与频域信号(施加x向激励)Fig.7 Time domain signal and frequency domain signal of the moving platform at edge position(applying x-direction excitation)

(a) 时域信号

(b) 频域信号图8 边缘位置处运动平台的时域信号与频域信号(施加y向激励)Fig.8 Time domain signal and frequency domain signal of the moving platform at edge position(applying y-direction excitation)

由图可以看出，当运动平台处于中心位置处时，分别对其施加y向和z向激励，则运动平台沿激励方向振动，且振动频率与该沿该方向的理论固有频率相符合(误差分别为3.09%和0.89%)，这是由于中心位置处机构的刚度矩阵是解耦的，因此不同方向的刚度相互独立，不同模态矢量也是相互独立的，单方向的激励不会引起多个方向的振动。而当运动平台处于边缘位置时，不同方向刚度的耦合导致机构各阶模态矢量具有多方向耦合的特点，此时单方向的激励会引起运动平台多个方向的振动。在对运动平台施加x方向和y方向的激励时，运动平台会在至少三个平动方向上产生振动，振动频率以一阶固有频率和二阶固有频率为主。仿真结果与理论计算结果的高度拟合可以证明本文所建模型的正确性。

4 样机试验

为了进一步验证空间索并联机构的实际振动特性，本文研制了索并联机构的缩比样机，通过试验对机构不同工况下的振动规律进行进一步研究。

4.1 绳索刚度标定

在以往的关于索并联机构振动方面的研究中，往往将绳索建模为弹簧模型，其刚度可以表示为式(11)。为了避免绳索刚度误差对刚度矩阵以及后续试验效果的影响，本节对试验用绳索进行选型和刚度标定。

本文选取了三种不同的绳索，其直径分别为0.8 mm、1.0 mm、2.0 mm。取其原长为700.0 mm，通过拉伸试验机分别测试其伸长量与载荷之间的关系。绳索样本及拉伸试验过程如图9～10所示。不同绳索的伸长量与载荷的关系如图11所示。

图9 绳索样本Fig.9 Cable samples

图10 绳索拉伸试验Fig.10 Cable tension test

图11 绳索伸长量-载荷曲线Fig.11 Cable elongation-load curve

图11中曲线的斜率即为绳索的刚度。可以看出，绳索的在受拉时的伸长量与载荷并不呈严格的线性关系，其中绳索2表现出的线性度最好，因此该绳索具有衡定的刚度。绳索1次之，而绳索3在受拉时的伸长量与载荷表现出较差的线性相关度，这是因为绳索3是多层编织的，在受拉时内层和外层并不同时伸长，因此在初始阶段相同伸长量下绳索的载荷变化较小，而在后期随着内层和外层同时承受载荷，曲线3的斜率开始增大，表现为绳索的刚度增加。这种情况下，采用式(11)的绳索刚度模型将产生较大的误差。综合考虑，本文选用第2种绳索，其在受拉时表现出恒定的刚度，符合式(11)的绳索刚度模型。

4.2 缩比样机振动特性试验

图12为空间索并联机构1∶15缩比样机。整体由框架、驱动单元、绳索和运动平台组成。驱动单元包含了电机、卷轴、绳索拉力传感器和滑轮。运动平台的振动由相机进行监测。类比4.1节设置运动平台的位置以及绳索张力。计算得到不同位置处样机的各阶模态(表4～表5)。

图12 空间索并联机构缩比样机Fig.12 Scaled prototype of the cable-and-parallel mechanism

表4 中心位置处样机的各阶固有频率和模态矢量Tab.4 The natural frequencies and modal vectors of the prototype at the center position

表5 边缘位置处样机的各阶固有频率和模态矢量Tab.5 The natural frequencies and modal vectors of the prototype at the the edge position

在对运动平台施加不同方向的激励后，测得样机的时域信号以及快速傅里叶变换后的频域信号如图13～图16所示。

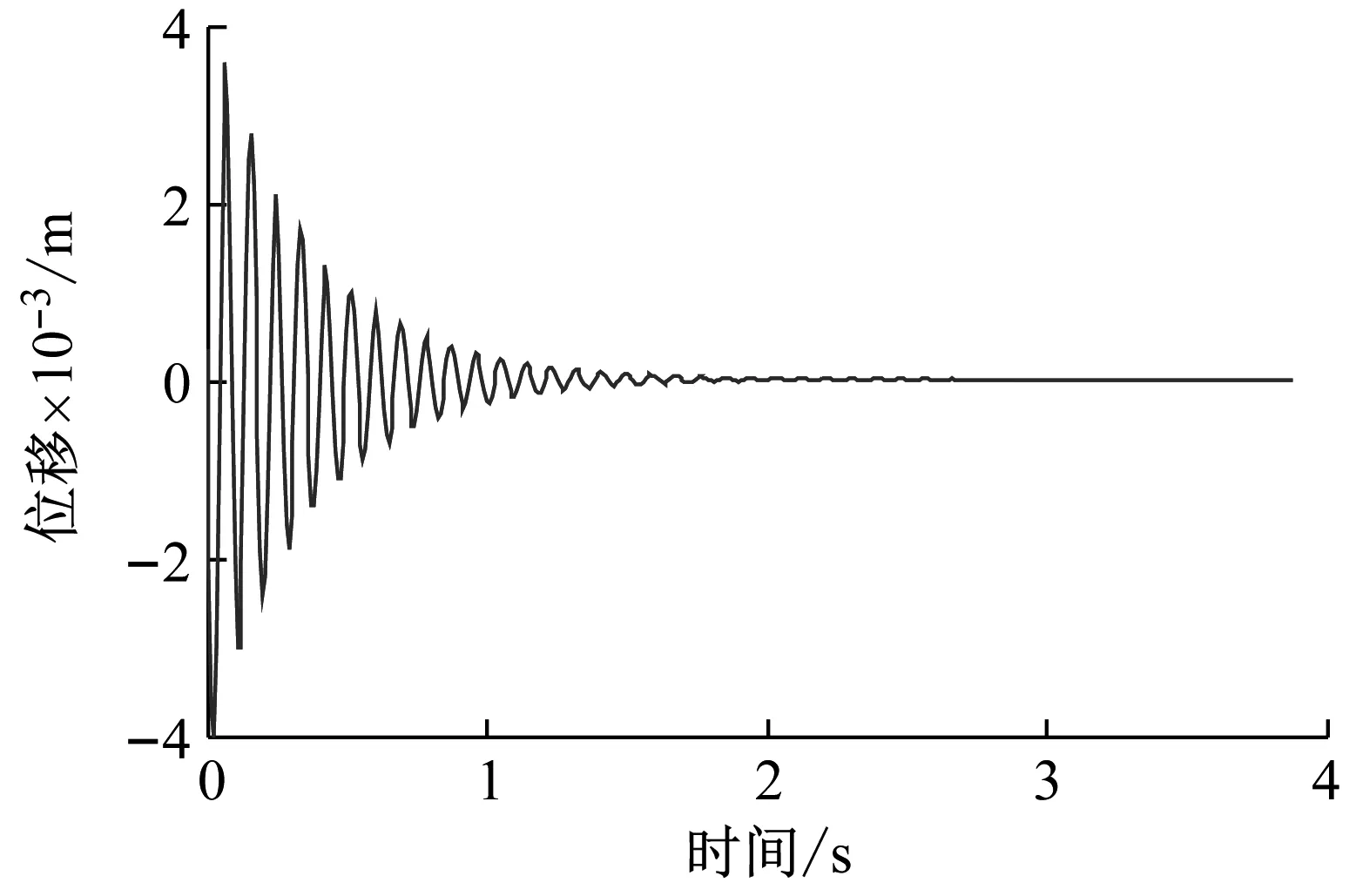
(a) 时域信号

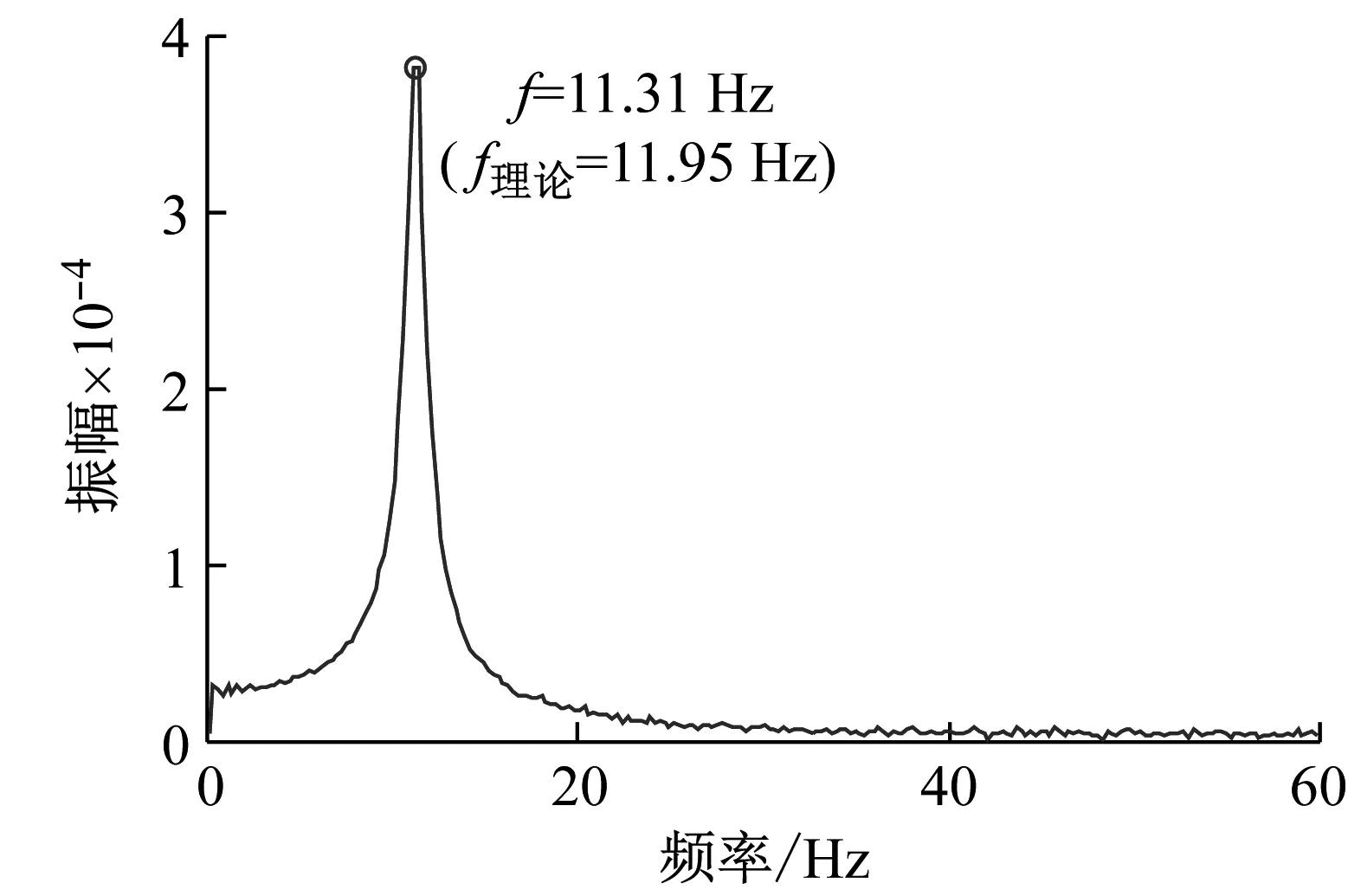
(b) 频域信号图13 中心位置处运动平台的时域信号与频域信号(施加y向激励)Fig.13 Time domain signal and frequency domain signal of the moving platform at the center position (applying y-direction excitation)

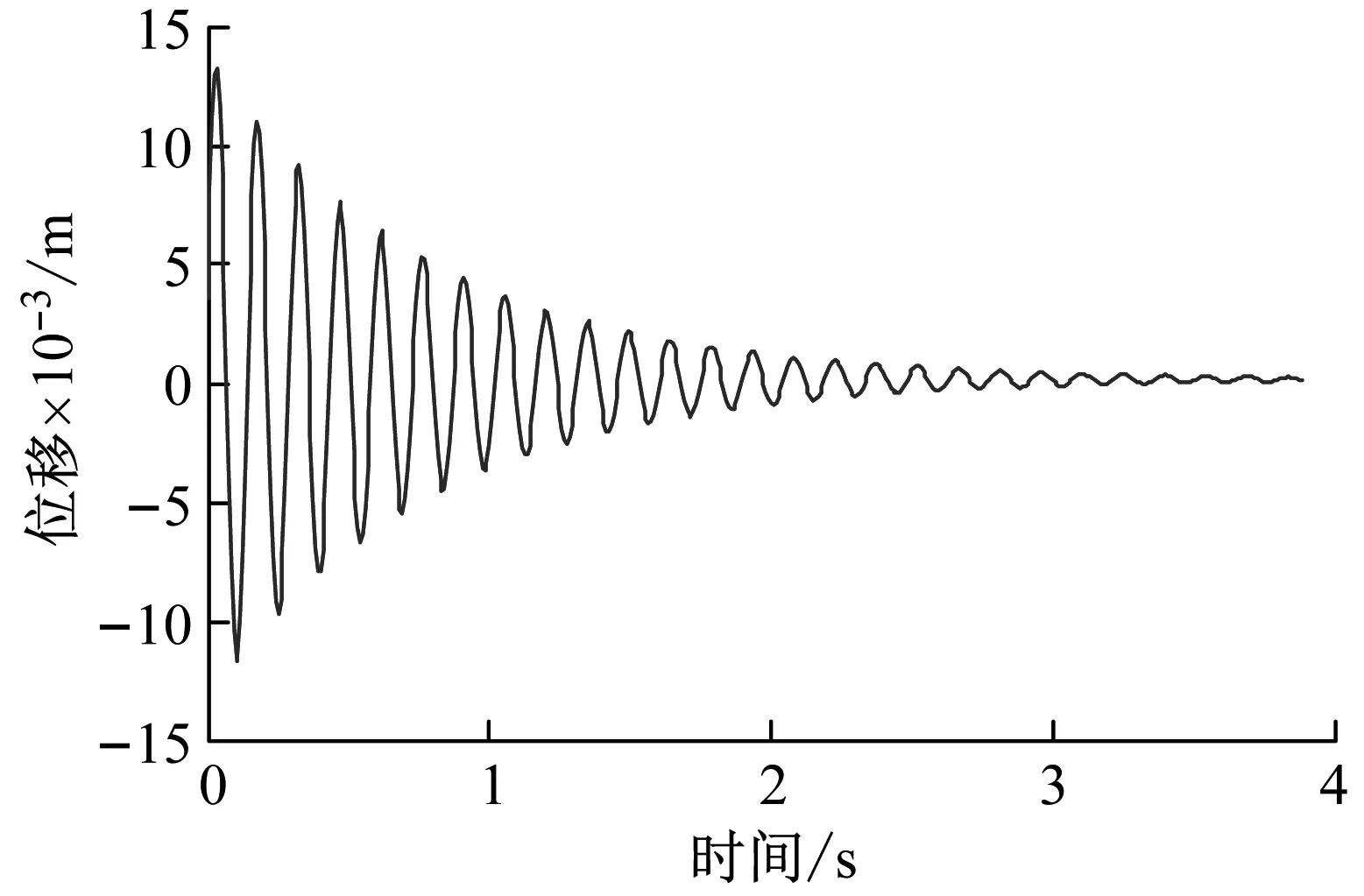
(a) 时域信号

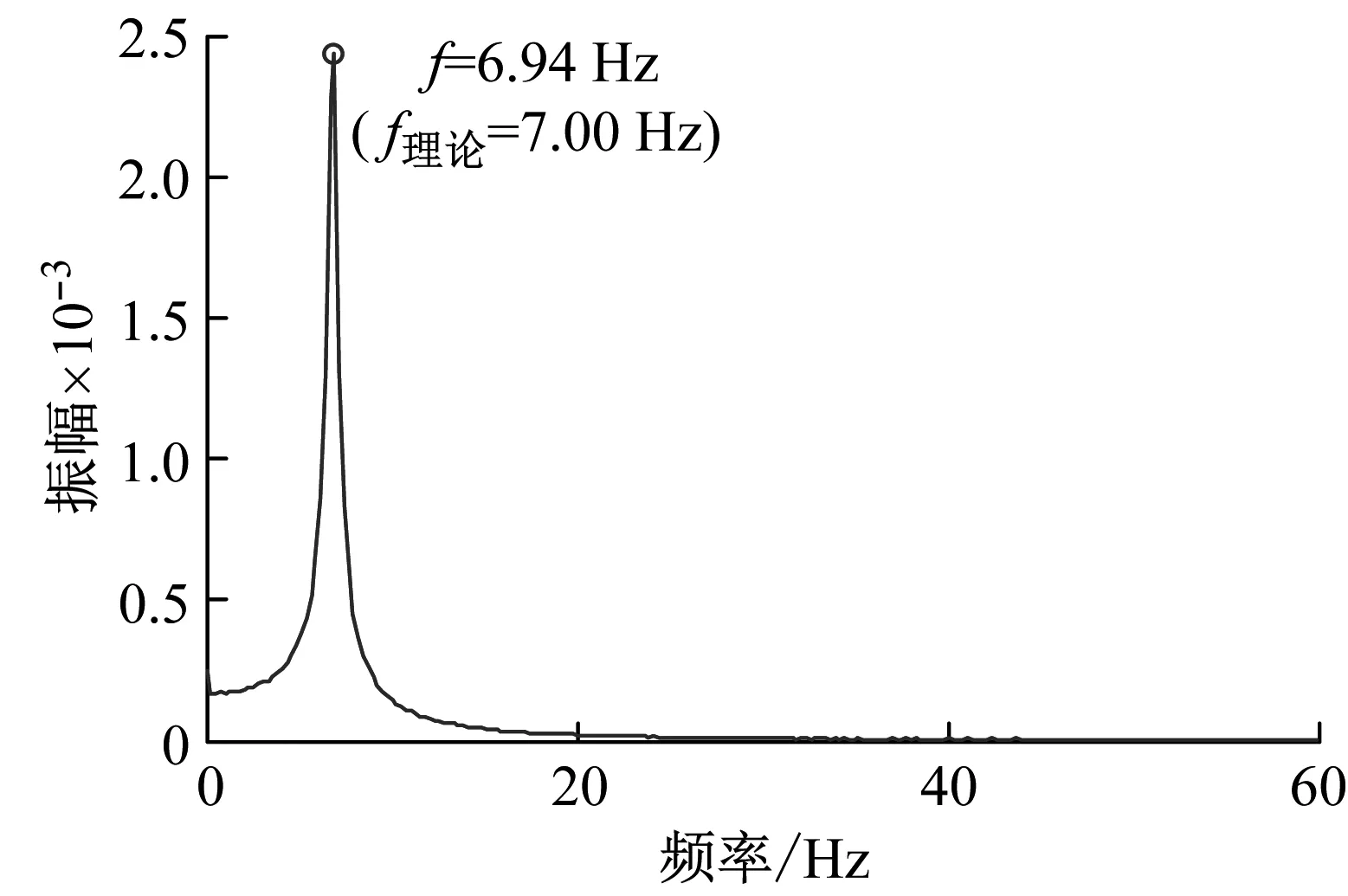
(b) 频域信号图14 中心位置处运动平台的时域信号与频域信号(施加z向激励)Fig.14 Time domain signal and frequency domain signal of the moving platform at the center position (applying z-direction excitation)

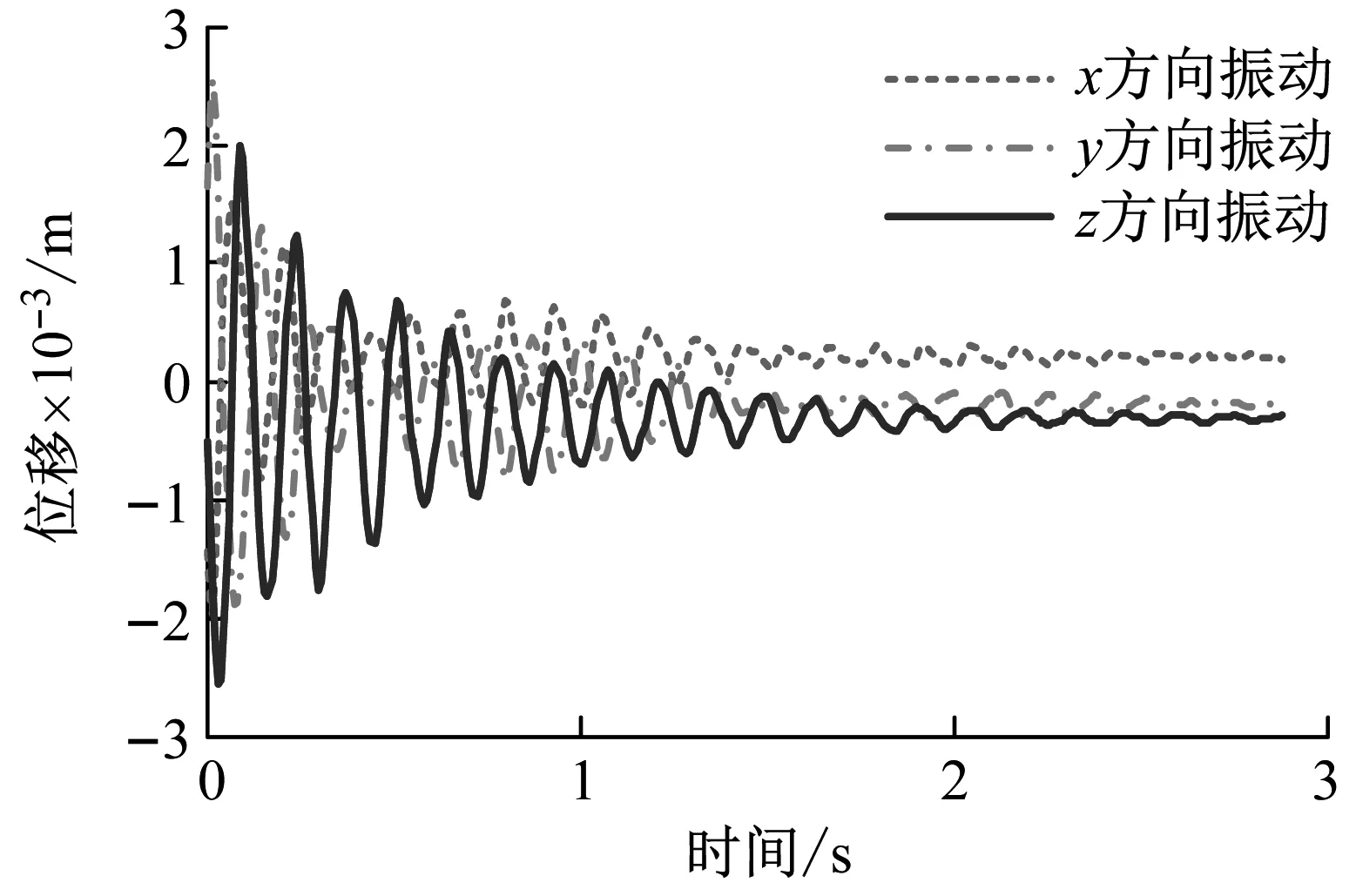
(a) 时域信号

(b) 频域信号图15 边缘位置处运动平台的时域信号与频域信号(施加y向激励)Fig.15 Time domain signal and frequency domain signal of the moving platform at edge position(applying y-direction excitation)

(a) 时域信号

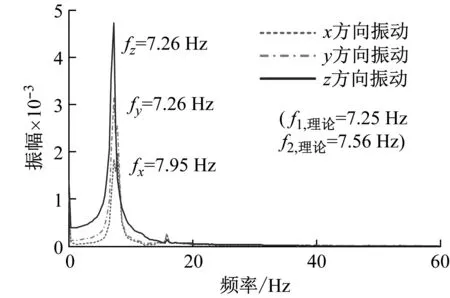
(b) 频域信号图16 边缘位置处运动平台的时域信号与频域信号(施加z向激励)Fig.16 Time domain signal and frequency domain signal of the moving platform at edge position(applying z-direction excitation)

可以发现在运动平台处于中心位置处时，分别对其施加y向和z向激励，运动平台沿激励方向振动，且振动频率与该沿该方向的理论固有频率具有较高的拟合性。在运动平台处于边缘位置时，对运动平台分别施加y方向和z方向的激励，运动平台会在至少三个平动方向上产生振动，振动频率仍以一阶固有频率和二阶固有频率为主。样机试验结果与仿真得出的结论相一致，进一步验证了本文所建模型以及所得出的索并联机构振动规律的有效性。

5 结 论

本文对一种空间冗余索并联机构的振动特性进行了研究。通过理论计算、仿真以及样机试验相结合的方式分析了不同工况对机构振动特性的影响，得到以下结论：

(1) 在采用高弹性模量的绳索时，机构的被动刚度较大，此时采用提高绳索拉力来增加机构主动刚度从而提高其固有频率的效果十分有限。相对而言，运动平台的位姿对于机构固有频率的影响较为明显。

(2) 运动平台在中心位置处时机构不同方向的刚度是解耦的，导致机构各阶模态矢量相互独立，不同方向的振动互不影响。

(3) 在边缘位置处，机构不同方向的刚度表现出强耦合性，其各阶模态矢量也具有相同的特点，表现为单方向的干扰力会引起多个方向的振动，且振动频率以一、二阶固有频率为主。

本文研究结果对于索并联机构的振动控制具有指导意义。