基于STA/LTA改进的CEEMD-SVD微震信号降噪算法

史艳楠， 齐朋磊， 王 裕， 王毅颖,2， 张冲冲

(1.河北工程大学 机械与装备工程学院，河北 邯郸 056038；2.河北省煤炭生态保护开采产业技术研究院，河北 邯郸 056038；3.邯郸市智能车辆重点实验室，河北 邯郸 056038)

近年来，随着我国大型水利水电工程不断建设及矿产资源开采进入深部，深部工程造成的岩石爆裂等地质灾害问题日益显著，严重影响了高效施工及安全生产。岩爆是深部工程开挖卸荷过程中，岩石中储存的弹性能突然释放导致岩体结构发生变化的现象[1-2]，因此获取岩爆发生的信息并掌握其规律是十分必要的。微震监测通过对岩爆过程中产生的信号进行检测和分析，可以实现对微震事件的超前预测与预报，被广泛应用于深埋隧道、大型水电站、矿井深部开采等深部工程[3-4]。因此，迅速、精确的识别岩石爆破所形成的微震信号尤为重要。但深部工程环境条件恶劣，检波器采集到的微震信号中往往会含有大量噪声信号，这些噪声与有效微震信号混叠在一起，会极大的干扰到微震信号的识别、初至拾取和震源定位。微震信号降噪方法研究对提高微震事件监测预警的准确性具有十分重要的现实意义。

目前，信号降噪主要以采用基于傅里叶变换的方法为主，但这种方法主要针对平稳信号具有良好的降噪效果。由于采集到的微震信号为非线性时变信号，采用传统方法时降噪效果较差，针对此问题文献[5]提出将卡尔曼滤波的方法应用于微震信号的降噪中，解决了传统降噪方法处理非线性时变信号效果差的问题。同时，随着小波技术的发展，利用其多分辨率特性，自适应的对低频部分和高频部分的信号进行辨别，成为有效处理非平稳信号局部特征的工具[6-7]。文献[8-9]将小波技术应用于微震信号的预处理，对采集到的信号进行了很好的滤波和降噪，证明小波技术可以实现微震信号的降噪；文献[10]将小波阈值算法应用于岩体结构监测的降噪，不仅提取出了低信噪比的有效微震信号，而且还实现了对频率范围广的岩体结构微震信号中有用信号和噪声信号的分离。但小波算法的基函数及阈值等参数需要根据工作环境确定，增加了算法调试时间，适应性不好。因此，国内外许多学者将Hilber-Huang(希尔伯特黄)的EMD应用到微震信号的降噪中，解决了小波算法预设参数的问题，该方法具有良好的时频特性，能够处理非线性、非平稳信号，通过将微震信号分解为不同的IMF，更能反映信号本身固有的属性，自适应好[11-12]。文献[13-14]利用EMD算法的自适应性，将振动信号分解成IMF，根据IMF固有属性，重组振动信号，提高了信号的信噪比，获得了较为明显的降噪效果。文献[15]采用EMD分解与独立成分分析结合的方法，优化了对IMF分量的选取，并对分界分量进一步去噪，充分保留有效微震信号的特征。在使用EMD降噪时，一个IMF分量中存在不同时间尺度的特征，出现模态混叠的现象，降低去噪效果。文献[16]提出了基于EEMD的算法，该算法加入均匀分布的噪声信号，使原信号频率分布趋于均匀，有效解决了模态混叠的现象，却无法在多次分解中得到的相同的固有模态函数的数量，需要更多次数的计算，效率下降。文献[17]通过计算EEMD各IMF分量的STA/LTA值来选取适合的IMF分量重构信号。分量的STA/LTA值可以反应信号的部分特征，可以有效的去除噪声分量。文献[18]提出EEMD-Hankel-SVD的方法对微震信号进行降噪，通过对高频分量的去除和低频分量的降噪，有效保留了信号原始特征，提高了信噪比和初至拾取效果。文献[19]针对传统消噪方法的不足，提出改进型CEEMD-SVD消噪方法对高边坡变形数据进行处理，消噪效果良好，该方法在一定程度上可以反映原始信号中的细节信息，但会造成有用信息损失。

基于以上分析，本文提出了一种基于STA/LTA改进的CEEMD-SVD微震信号降噪方法，本文算法采用将正负白噪声加入原始信号后，进行EMD分解，计算各IMF分量的STA/LTA值，通过阈值来判定是否对其进行SVD分解。集总平均IMFi，得到降噪后信号。CEEMD是对EEMD进一步改进，集总平均次数会减少，从EEMD的百量级减小到CEEMD的几十的量级，重建后的信号噪声明显减少。本文方法提高了信号预处理的效率，减小了重构误差，有效的保留了原始信号的特征，很好的压制了噪声信号，为信号后续研究提供了高信噪比的数据，为微震活动特征及规律性研究分析奠定基础。

1 基本理论

1.1 CEEMD

CEEMD算法是对EMD算法的进一步优化，在原始信号中加入n对不同的正负白噪声，用于抵消信号中加入的白噪声。对两个信号分别进行EMD模态分解。求得各IMF分量的均值，再对n组IMF集总平均得到重构信号。具体算法流程如图1所示。

图1 CEEMD流程图Fig.1 The flow chart of CEEMD

算法的实现步骤如下：

在原微震信号s(t)中分别加入和减去n个均值为0、幅值和标准差为常数的高斯白噪声n(t)，得到新的重构信号

xia(t)=si(t)+ni(t)

(1)

xib(t)=si(t)-ni(t)

(2)

式中:xia(t)为加入第i个高斯白噪声信号后的复合信号;xib(t)为减去第i个高斯白噪声信号后的复合信号;ni(t)为加入的第i个高斯白噪声信号。

1.2 SVD

SVD算法是通过把时间序列信号矩阵化分解的方法，将一维信号转换为矩阵进行运算分解，而构建矩阵方算法众多，主要有Toeplitz矩阵和Cycle矩阵及Hankel矩阵，使用不同的矩阵构建方法，SVD分解处理信号的效果是不一样的。本文采用构建Hankel矩阵，然后进行SVD分解时，得到一系列的奇异值，每个奇异值对应不同的频率幅值，想要提取的特征信号，只需提找出对应的奇异值，并把剩余奇异值归0即可。根据这一特性，通过加入与原信号相关的频率约束信号，放大该频率的k个奇异值，将剩余奇异值归0，再进行奇异值分解逆变换，并将加入的约束信号去除，即可提取出信号中有用信息。构建Hankel矩阵进行SVD分解的过程如下：

对于信号x={x1,x2,…,xi}，i=1,2,…,M。可以构建如下Hankel矩阵

(3)

式中，m+n-1=M,m≥n。根据文献[20]可知，当m=M/2时，使用Hankel矩阵进行SVD降噪效果最佳。

对D进行奇异值分解，得到

(4)

式中:A、B为正交矩阵;AT为A的转置;Σ为对角方阵，其对角元素由奇异值组成，且奇异值存在如下关系：β1>β2>…>βk>0，式中βk为奇异值分解得到的第k个奇异值，xi、yi是矩阵A、B的第i个列向量，r为矩阵D的秩。

2 基于STA/LTA的CEEMD-SVD算法

CEEMD算法与EMD算法有一些相同的特征，在其IMF分量中，在排列靠前的几个分量是高频分量，包含大量的随机噪声，通过STA/LTA阈值可以去除大量的含燥分量。而舍弃的IMF分量中仍包含有用的信号，直接舍去会影响到重构之后的信号波形，无法完全体现原有的特征信息，相应评价指标无法达到最佳。若对含噪声信号直接采用传统SVD降噪，则对奇异值的选取困难信号频率范围达不到理想状态。因此采用基于STA/LTA的CEEMD-SVD方法进行降噪，选择不符合阈值要求的IMF分量进行SVD分解降噪，以充分保留高频IMF成分中的有用信息，降低了有用信息的损失，使重构后波形与各项指标达到最优化。算法流程图如图2所示。

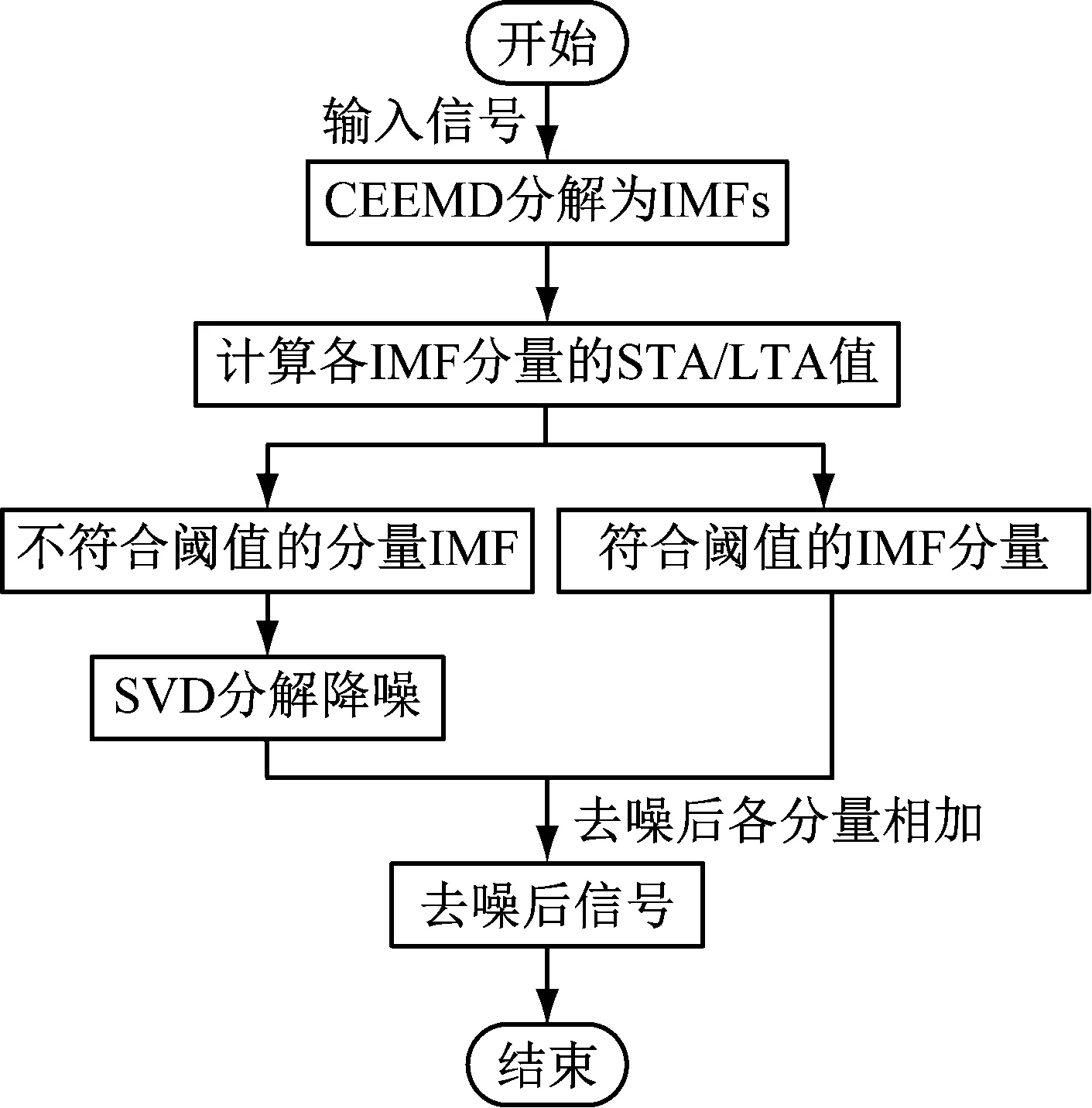
图2 算法流程图Fig.2 Algorithm flow chart

降噪实现步骤如下：

(1) 对原含噪声信号进行CEEMD分解，得到最终分解的一系列IMF分量。

(2) 设定STA/LTA算法的阈值ε，ε的取值根据实际信号以及时窗长度进行选取[21]。

(3) 计算各IMF分量的STA/LTA值；舍去不符合要求的分量。

(4) 将保留的IMF分量的和作为频率约束条件，加入到舍弃的IMF分量中，分别进行SVD分解，提取有用信号。

(5) 将提取到的有用信号与最终残余分量求和，即得到降噪后的信号。

3 仿真实验分析

为了验证本文提出方法的有效性和降噪效果，采用实测微震信号通过LabVIEW平台进行试验，并与EMD、EEMD和SVD降噪效果进行对比、分析。

3.1 降噪效果评价

为了更好的说明算法的有效性，本文采用信噪比(SNR)、能量保持百分比(E)以及信号标准差(RMSE)作为评价指标。其定义

(5)

E=Ex/Ey

(6)

(7)

式中:y(n)为降噪后信号;x(n)为有用信号;N为采样点数;Ex为有用信号能量;Ey为含噪声信号能量。

3.2 仿真分析

为验证本文算法降噪效果，在原有用信号中加入噪声进行仿真模拟。本文采用某矿采样时间段长度为4 000个采样点的微震信号进行模拟仿真分析[22]。图3(a)为原微震信号的幅频特性图3(b)含5 dB噪声微震信号的幅频特性。

(a) 原信号的波形及幅频特性

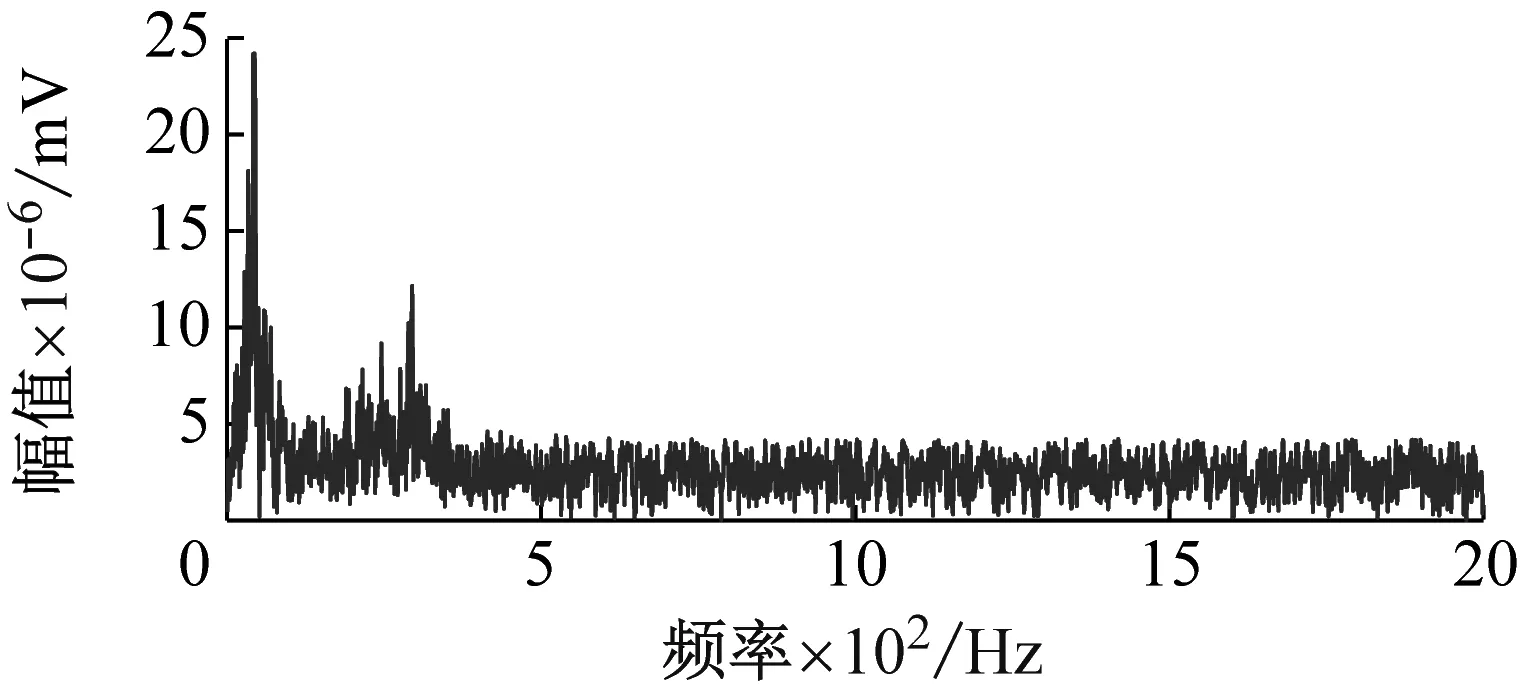
(b) 含噪微震信号的波形及幅频特性图3 原信号及含噪微震信号的波形及幅频特性Fig.3 Waveform and amplitude-frequency characteristics of the original signal and the noisy microseismic signa

对图3(b)含燥微震信号进行CEEMD分解，得到11个IMF分量，如图4所示。对图3(a)原信号的幅频特性分析可知不含噪声信号的频率主要咋0～500 Hz之间，从图4(a)和图4(b)中可以看出IMF1、IMF2的波形噪声污染较为严重，频率分布宽泛与原信号相差较大。IFM3以后的分量波形较为平滑，振动趋势与原信号相似，且频率范围主要在0～500 Hz之间，集中在原信号频率范围附近。

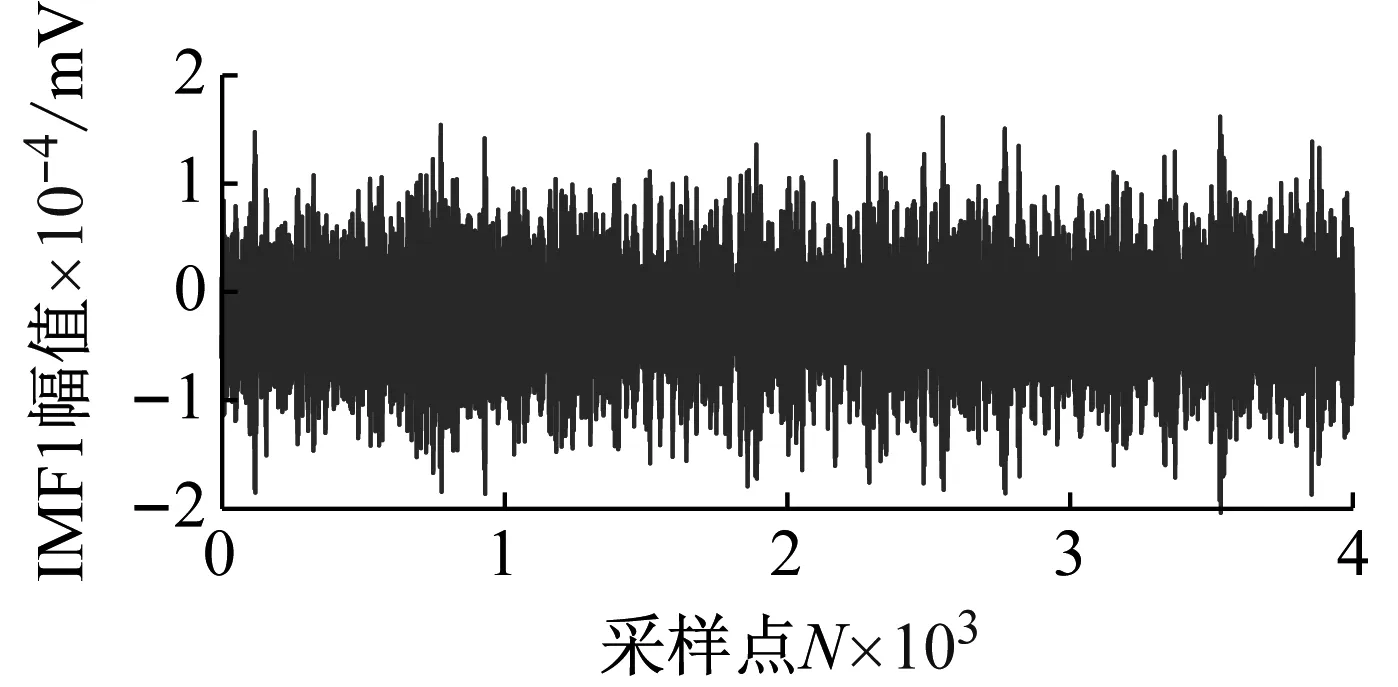
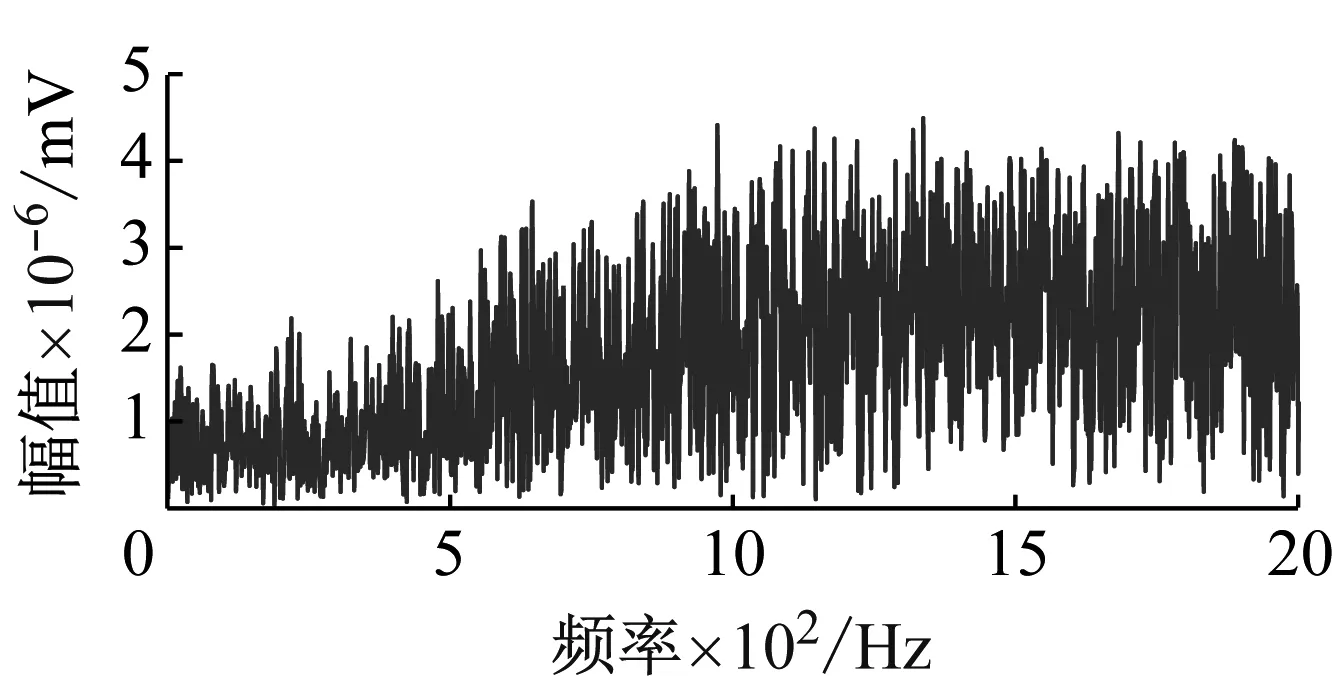
(a) IMF1的波形及幅频特性

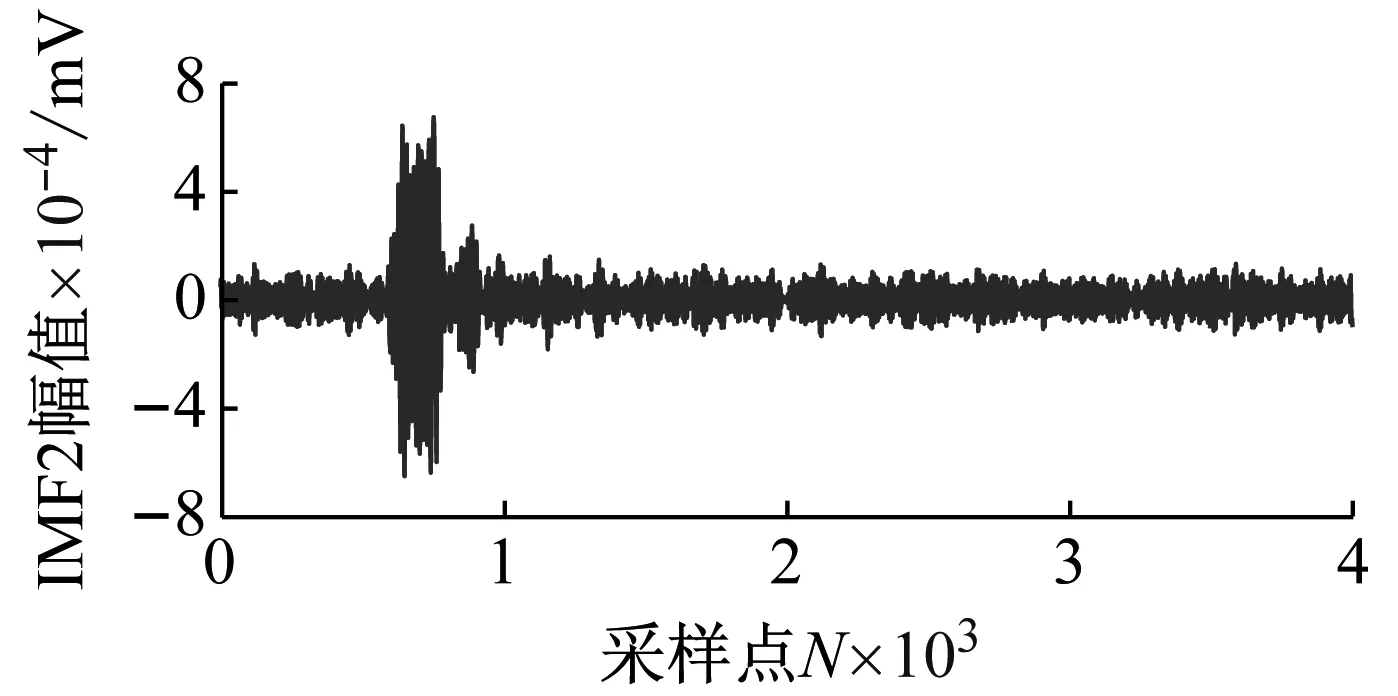
(b) IMF2的波形及幅频特性

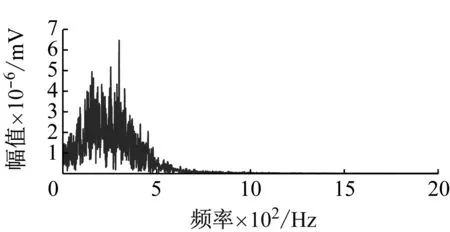
(c) IMF3的波形及幅频特性

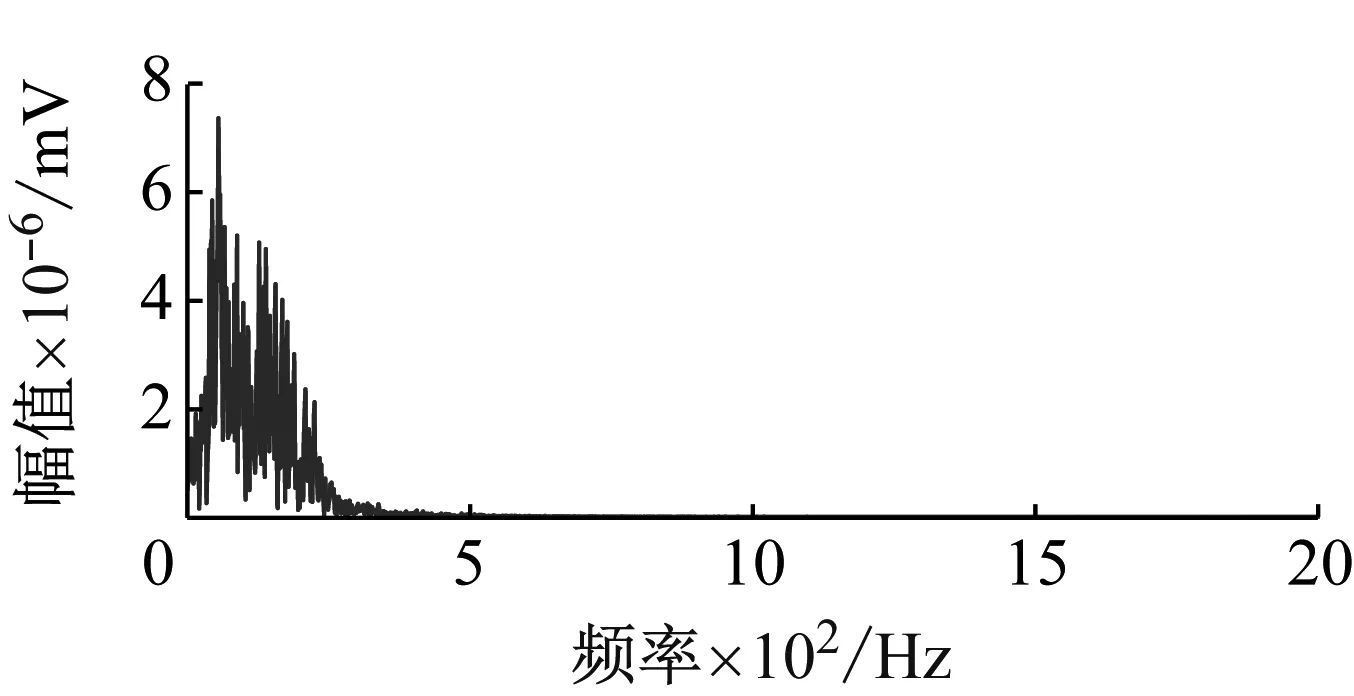
(d) IMF4的波形及幅频特性

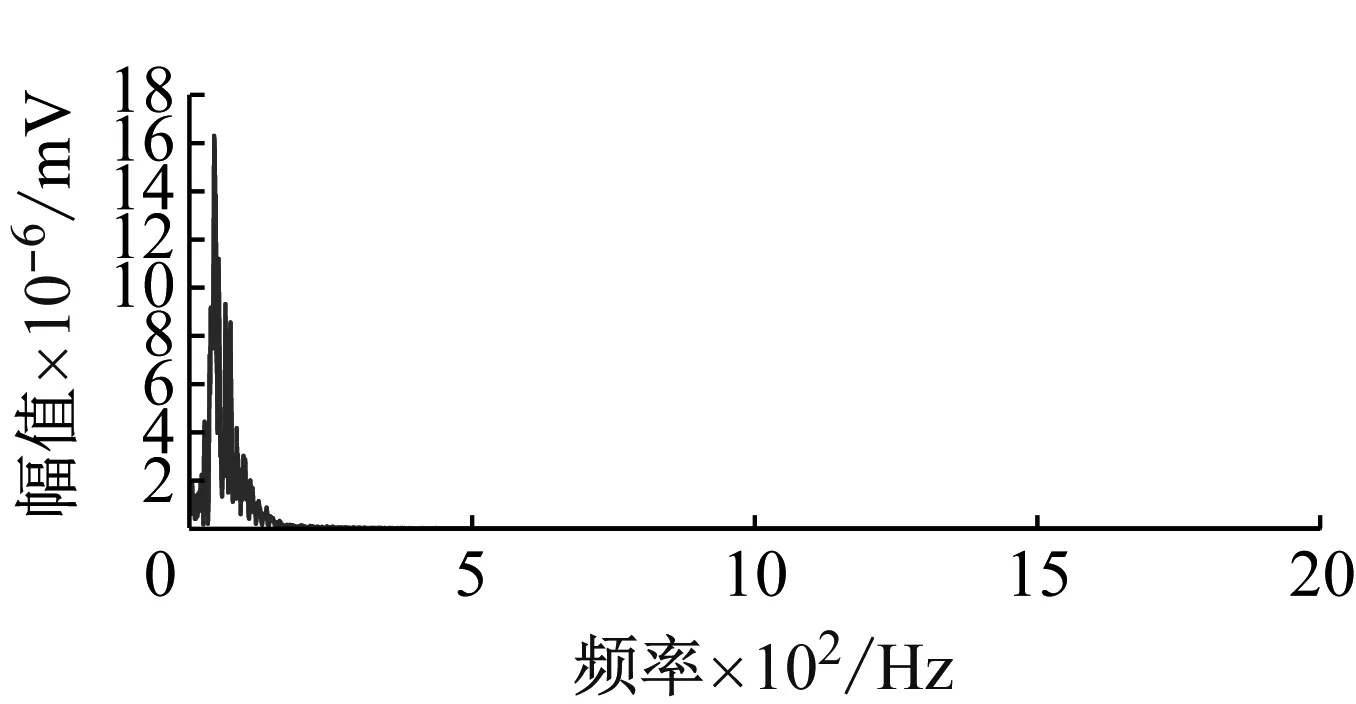
(e) IMF5的波形及幅频特性

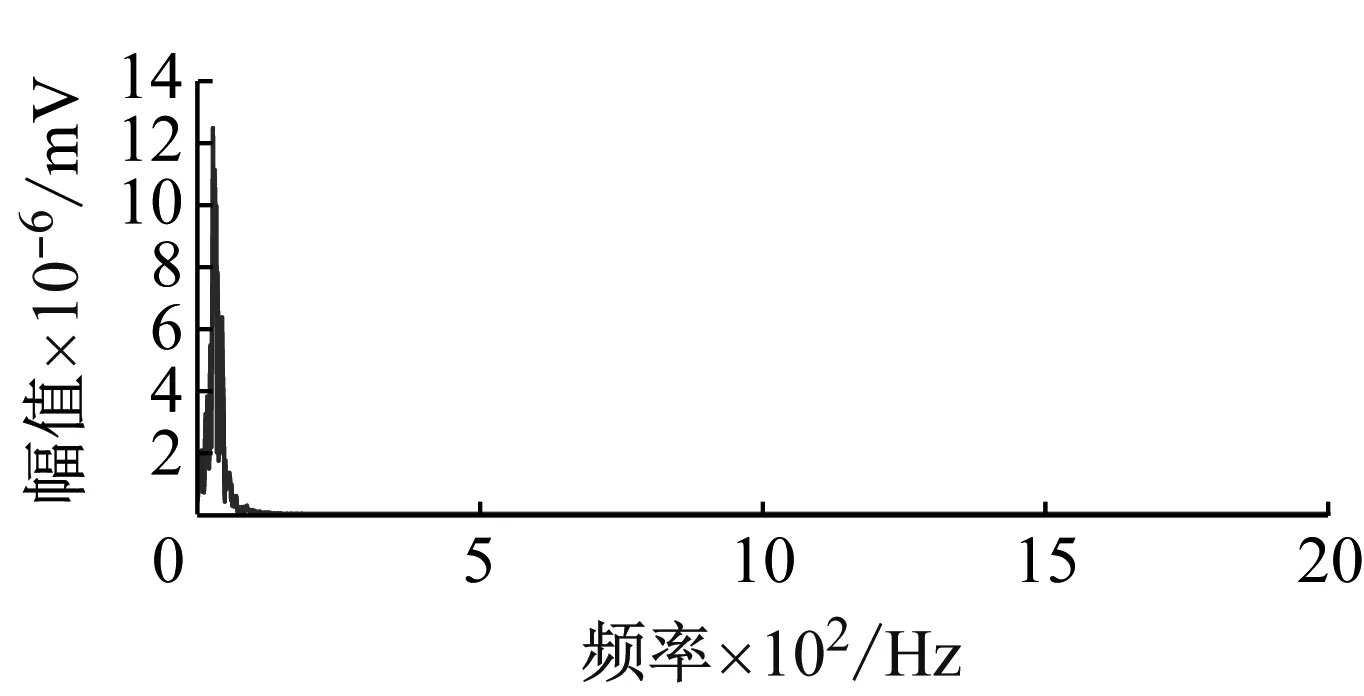
(f) IMF6的波形及幅频特性

(g) IMF7的波形及幅频特性

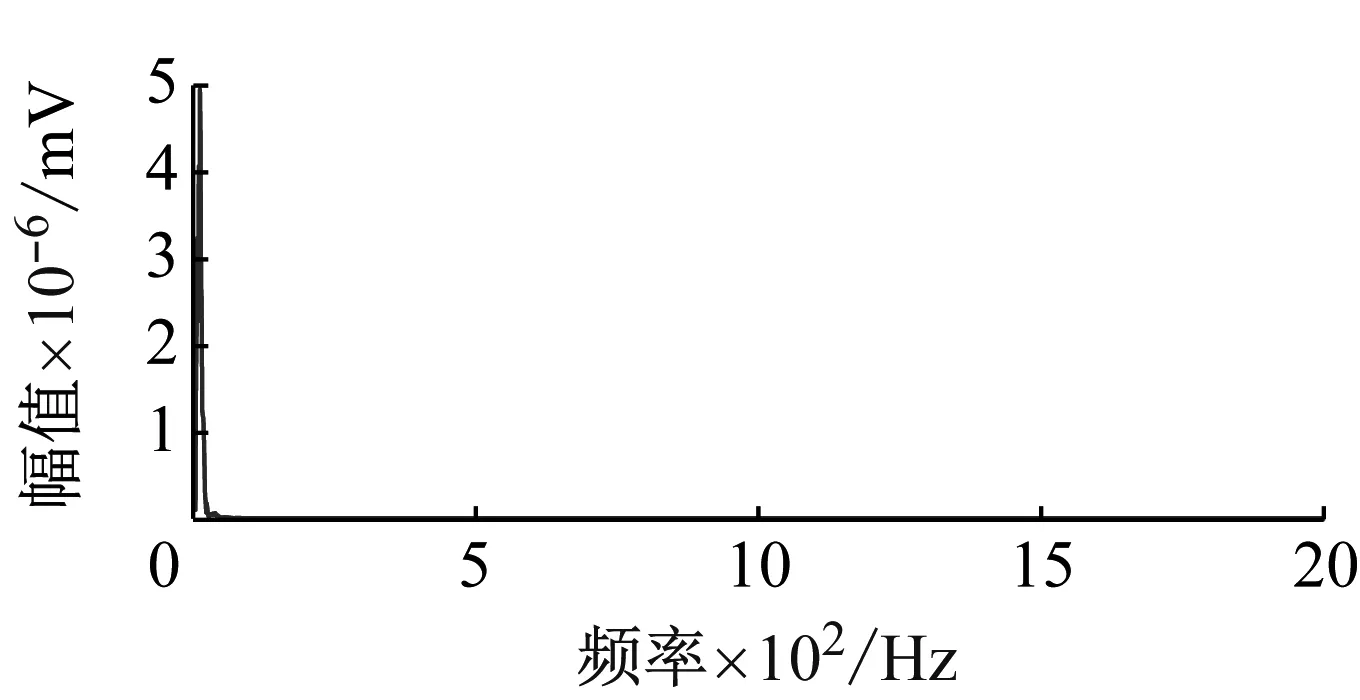
(h) IMF8的波形及幅频特性

(i) IMF9的波形及幅频特性

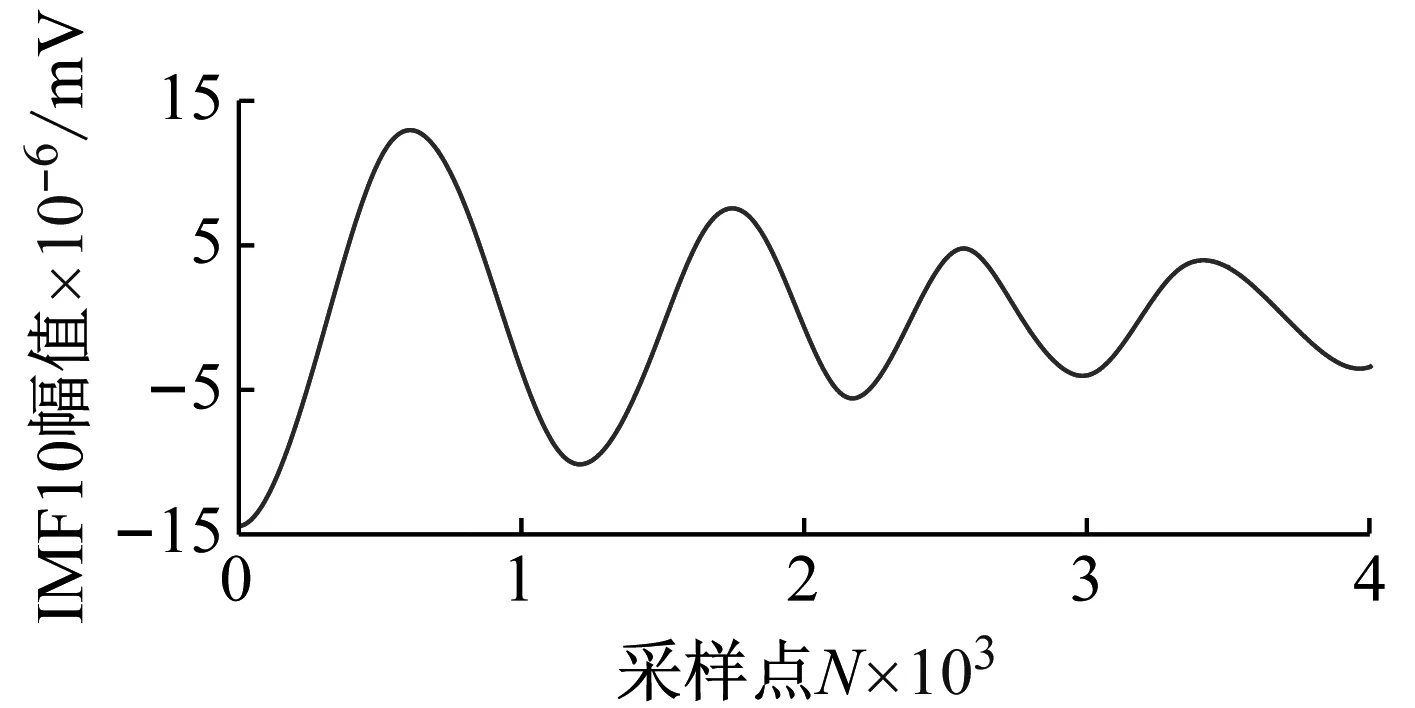
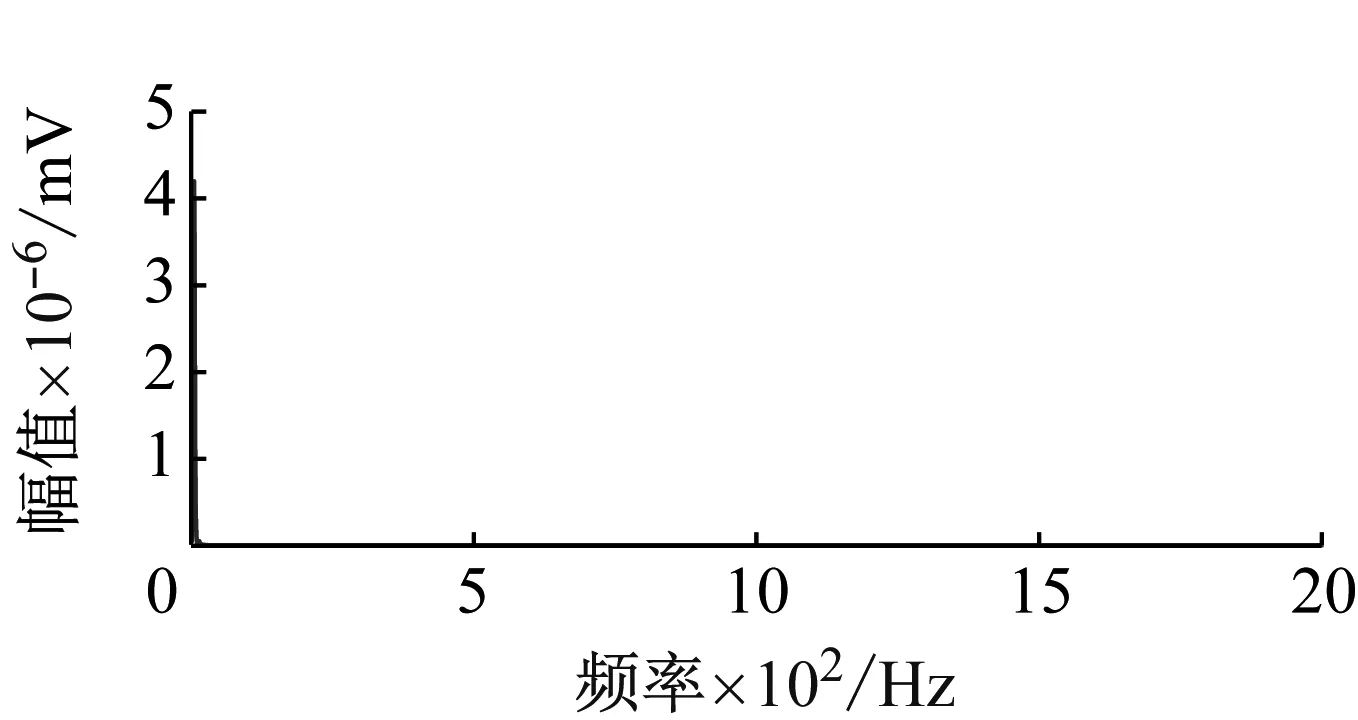
(j) IMF10的波形及幅频特性

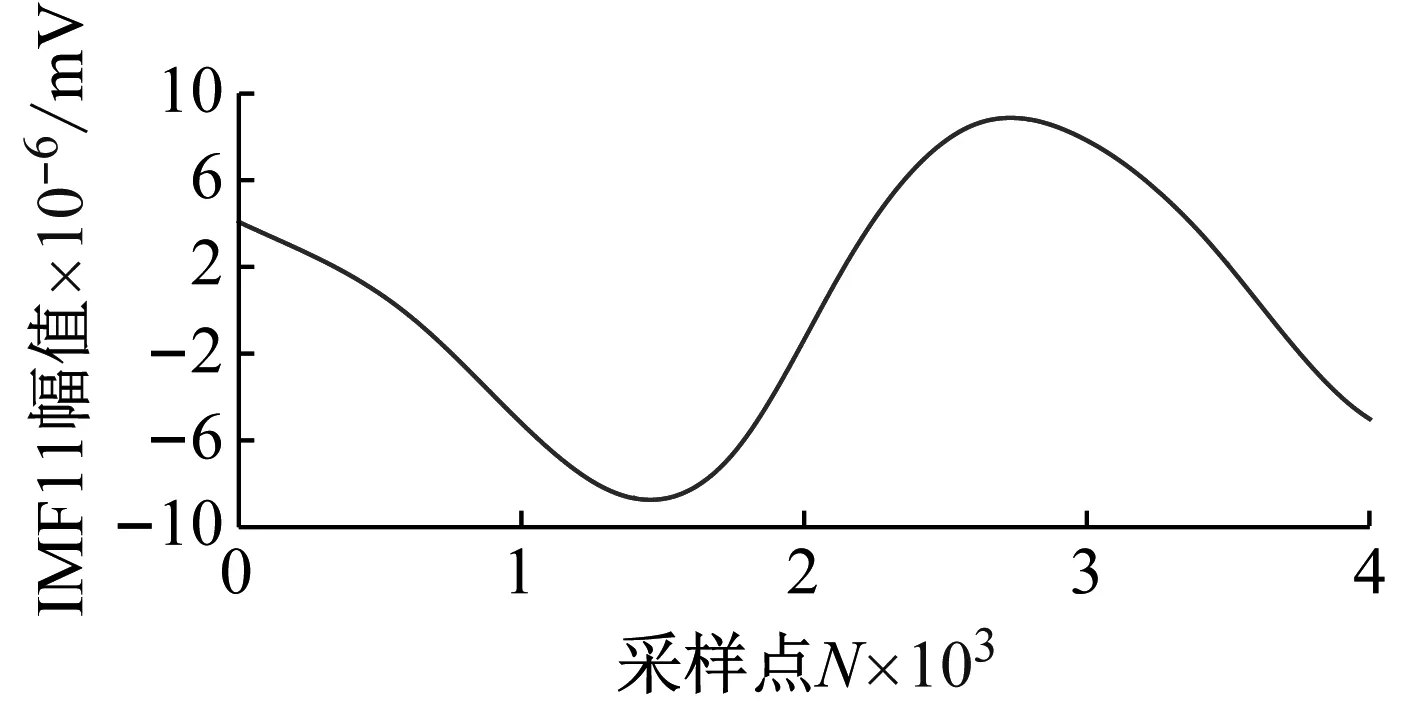
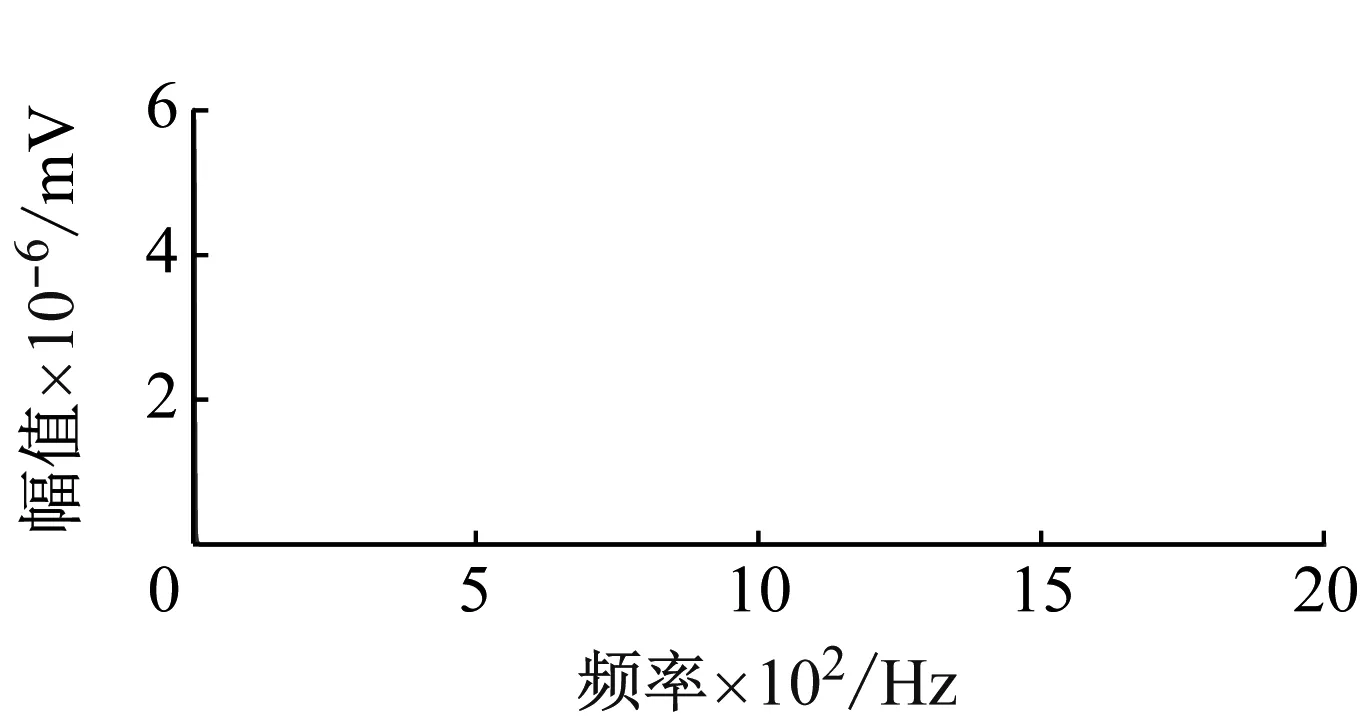
(k) IMF11的波形及幅频特性图4 各IMF分量的波形及幅频特性Fig.4 Waveform and amplitude-frequency characteristics of each IMF

为了解决CEEMD算法产生的伪分量现象，通过结合STA/LTA算法，可以去除包含大量噪声信号的IMF分量。求各分量的STA/LTA值如图5所示，通过分析长短时窗的长度，本文设定阈值为2，重构信号预选取IMF2～IMF7及IMF9等7个分量为重构信号的子频段信号。

(a) IMF2

(b) IMF3

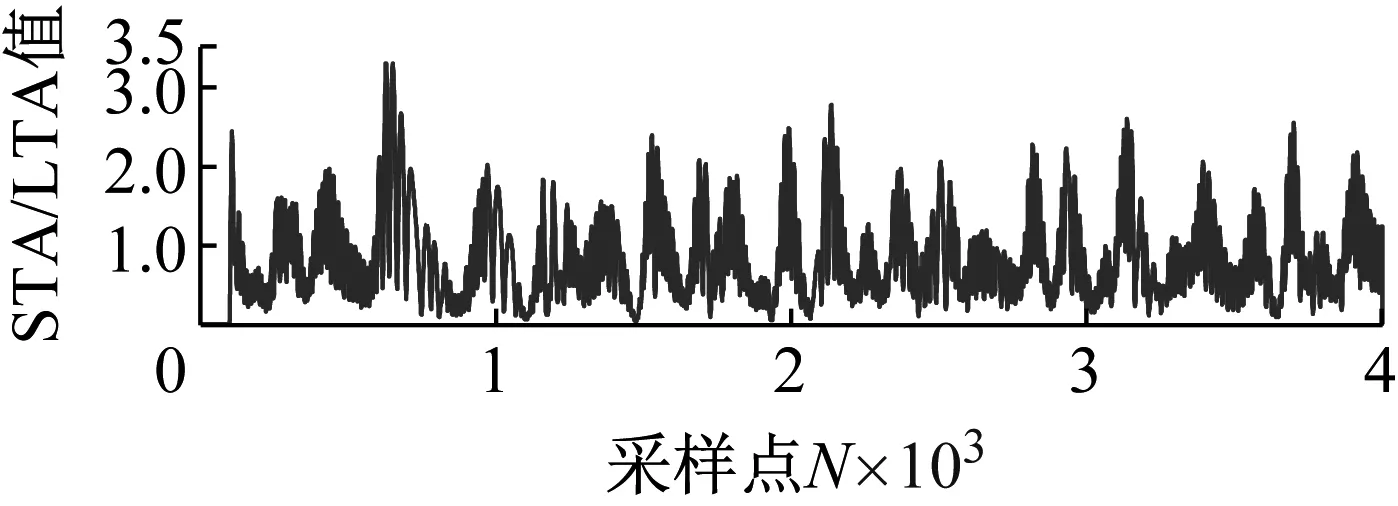
(c) IMF4

(d) IMF5

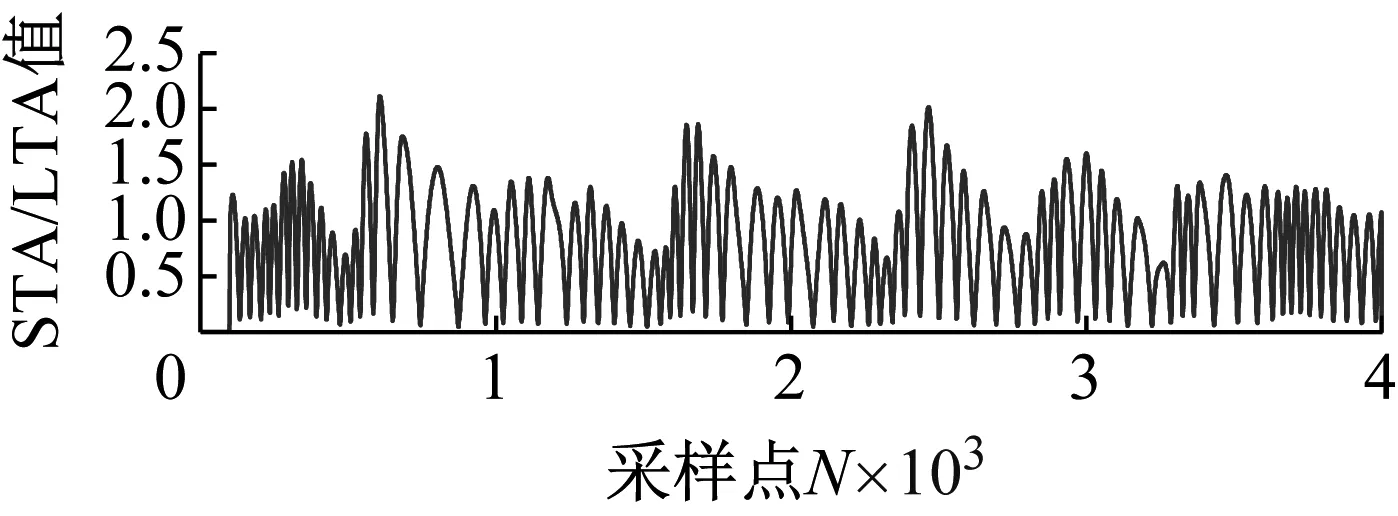
(e) IMF6

(f) IMF7

(g) IMF9图5 各IMF分量的STA/LTA值Fig.5 STA/LTA values of each IMF

计算各IMF分量与原微震信号的相关性如图6所示，可知MF3为分界IMF，进而确定信号主导的IMF分量为IMF3～IMF11，与STA/LTA算法相结合选取IMF3～IMF7重构信号。

图6 相关系数Fig.6 Correlation coefficient

对预选的IMF分量中的噪声主导的IMF1，IMF2进行SVD降噪。最后将噪声主导的IMF降噪后与IMF3～IMF7及残余分量进行信号重构，得到降噪信号，如图7所示。

(a)

(b)图7 重构微震信号波形及幅频幅频特性Fig.7 Reconstructed microseismic signal waveform and amplitude-frequency amplitude-frequency characteristics

通过本文算法得到的重构信号见图7，重构信号的频率范围与原信号频率接近。从表1可以看出重构后的信号信噪比、能量百分比及信号标准差较加噪信号都用明显提升。说明本文方法可以有效的降除噪声。

表1 降噪效果分析Tab.1 Analysis of noise reduction effect

3.3 实验分析

以某矿的微震监测系统采集到的微震信号为分析对象，对本文方法的降噪效果进行验证，实测含噪微震信号的波形图及幅频特性如图8所示。

(a)

(b)图8 含噪微震信号的波形及幅频特性Fig.8 Waveform and amplitude-frequency characteristics of noisy microseismic signals

从图8可以看出微震信号频率在0～100 Hz时幅值较大，有用的信号频率主要分布在该频率范围内，但信号中包含大量随机噪声，有用微震信号波形受到严重干扰。采用本文方法对该信号进行处理，同时对信号使用NAEEMD、EEMD和EMD三种方法进行降噪效果对比分析，采用各方法对微震信号降噪后的波形及幅频特性分别如图9所示，其中图9(a)为本文方法降噪，图9(b)为EMD分解降噪，图9(c)为EEMD分解降噪，图9(d)为NAEEMD分解降噪。

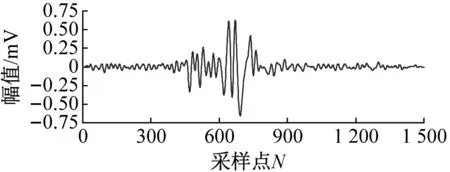
(a) 本文

(b) EMD

(c) EEMD

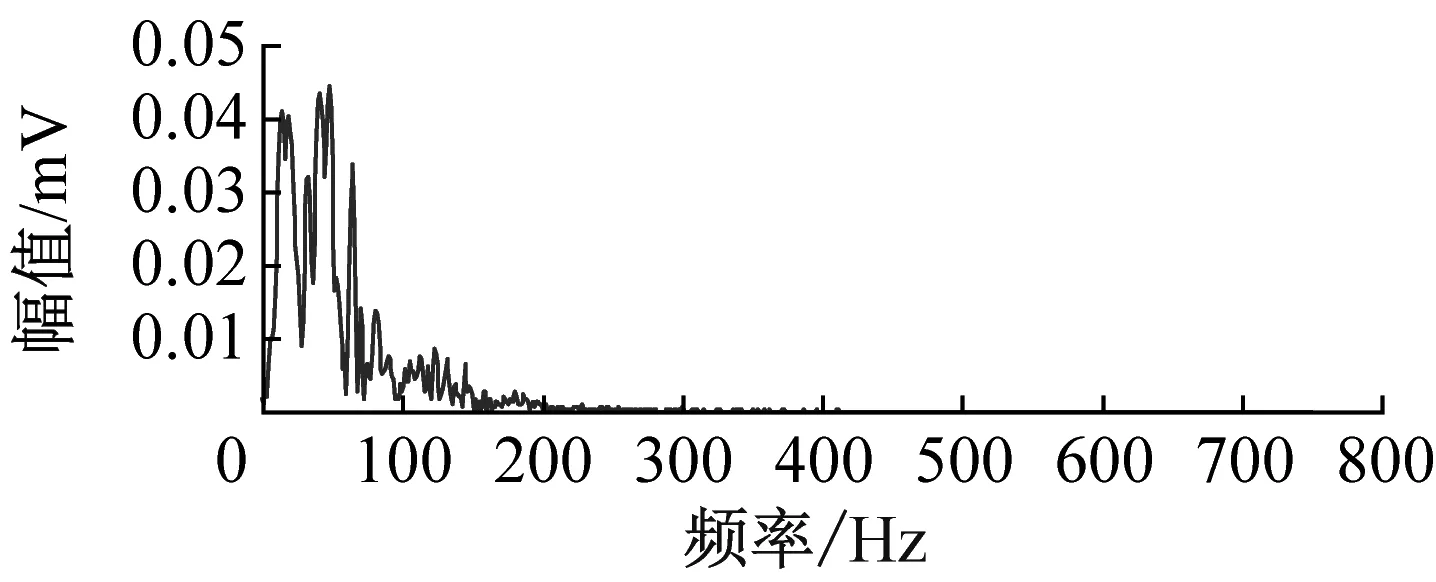
(d) NAEEMD图9 微震信号各方法降噪后波形及幅频特性Fig.9 Waveform and amplitude-frequency characteristics of microseismic signal after denoising by various methods

从图9可以看出，两段微震信号波形通过各降噪方法降噪后比降噪前波形更加清晰，且较好的保持了波形的变化趋势，幅频特性的优势频率分布更加明显。图9(a)中降噪后的波形平滑性较好，而图9(b)中的波形平滑性更好，但其波峰波谷的削弱较大，图9(c)和图9(d)的虽然波峰波谷没有明显削弱，但波形的平滑度较差；同时图9中频率范围集中在0～100 Hz，与图9(b)、(c)和(d)对比优势明显。

通过对各方法降噪前后的信噪比、能量百分比及信号标准差进行计算，结果如表2所示。从表2可以看出，微震信号经过4种方法降噪后，本文方法较其他方法的信噪比均高出5 dB以上，且信号的能量百分比高达95.586 7%，信号标准差达到了0.014 8，优于其他降噪方法。因此，应用本文方法对微震信号进行降噪不仅是有效的，而且较其他方法优势明显，具有更好的应用效果。

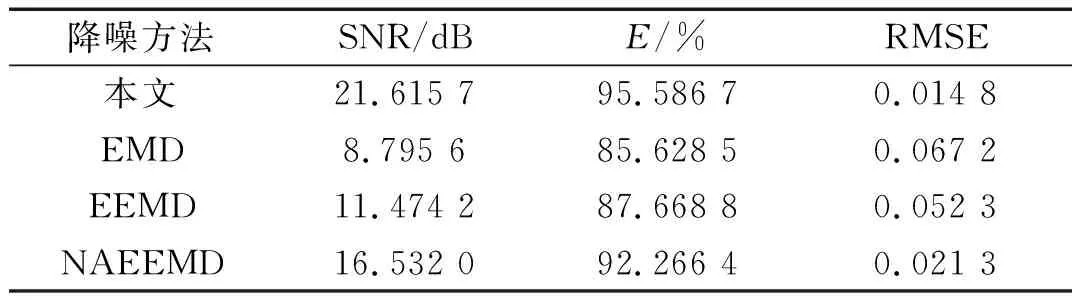
表2 微震信号降噪对比Tab.2 Noise reduction comparison of microseismic signals

4 结 论

(1) 对采集到的微震信号经过CEEMD分解，得到固有模态分量，利用STA/LTA确定保留的IMF分量和舍弃的IMF分量，然后对舍弃的IMF分量降噪，有效的获取IMF分量中信号主导分量，使得重构后的微震信号较好的保留了微震信号的波形特征，同时在CEEMD分解时通过对残差信号不断加入白噪声，并只进行一阶模态分解，因此，每次加噪后的误差不是通过独立分解得到的，而是由最后一次分解的误差得到的，很大程度上减少了分解后的重构误差。

(2) 通过模拟噪声信号进行仿真实验，验证了频率约束的可行性，经过对降噪后信号的信噪比、能量百分比及信号标准差计算，分别从5.013 32 dB，75.402%及0.034 5达到了15.670 1 dB，95.227%及0.021 9，信号降噪效果明显，能有效的去除信号中存在的随机噪声，证明了本文方法对微震信号进行降噪是有效的。

(3) 采用本文方法对某矿实测微震信号进行降噪分析，并与EMD，EEMD，NAEEMD降噪方法进行对比，结果表明本文方法可以有效的降低煤矿微震信号中的噪声干扰，且较其他方法优势明显，具有更好的应用效果。但仍需在深埋隧道、大型水电站等工程环境背景条件下进行进一步验证与优化。