大跨索屋盖结构风振动力计算新方法研究
毛吉化, 聂竹林, 汪大洋, 许 伟, 区 彤, 陈 伟, 吴福成
(1.广州大学 土木工程学院,广州 510006;2 广州广检建设工程检测中心有限公司,广州 510600;3.广东省建筑科学研究院集团股份有限公司,广州 510500;4.广东省建筑设计研究院有限公司,广州 510145)
大跨索屋盖结构具有大跨轻柔、频率密集、造型优美奇特等特点,广泛应用于机场航站楼、体育场馆、高铁车站和会展中心等大跨建筑中[1-2],是一座城市的地标和名片,更体现了国家建筑科技水平的发达[3]。由于这些特点也决定了大跨索屋盖结构轻柔特性[4-5],属于风敏感结构[6-7]。近年来我国沿海地区超强台风的频繁出现,对此类大跨屋盖结构的抗风安全带来了极大威胁,如:2015年10月台风“彩虹”湛江登陆,造成湛江奥体中心几个体育场馆屋盖严重掀毁;2017年8月台风“天鸽”珠海登陆后,珠海会展中心部分屋盖被掀毁;2018年9月台风“山竹”于珠海登陆,珠海网球中心索屋盖被严重撕毁。
大跨索屋盖结构的自振频率与风荷载的激励频率较为接近,且索结构往往表现出较为显著的非线性[8],决定了大跨索屋盖结构脉动风致振动效应显著,属于风敏感结构,风荷载是大跨索屋盖结构的主控荷载。索屋盖结构屋盖风荷载因结构特有的造型,在时间-空间上的分布特征极为复杂[9-10],风致振动响应具有较高的随机特性。王珩等[11]直接采用风洞试验得到的数据,运用时程分析方法计算台州体育中心屋盖的竖向风振系数,结果表明风振系数随风向角变化较为敏感,计算时应采取最不利风向角进行验算。韩志惠等[12]利用世博轴阳光谷刚片缩尺模型风洞试验的测压数据,分别采用频域的模态叠加法和时域的数值积分法,对结构进行线性风振响应分析,结果表明时域法计算的风振响应结果比频域的大。孙旭峰等[13]对肋环型索穹顶结构进行了耦合频域风振响应分析,耦合影响因素会导致结构风振位移响应和风振系数减小。徐牧[14]分别采用频域和时域方法对汉城体操馆Ceiger型索穹顶进行了计算分析,结果表明多数部位风振系数较为接近,但屋盖中心区域结果差别较大。
赵臣等[15]采用一种非线性动力微分方程对大跨悬索屋盖进行风振反应分析,结果证明了鞍型索网为风敏感结构,其垂跨比对脉动风响应起主导作用。冯若强等[16]采用Ritz-POD法选取结构主要振型,在频域内对大跨度鞍型索网屋盖进行了风振响应分析,结果表明采用Ritz-POD法能够较准确的得到结构的真实风振响应。李璟等[17]采用非线性有限元分析与人工智能神经网络相结合的方法对一大型索膜屋盖结果进行了风振动力响应分析,获得了风振系数随索膜张力和平均风速变化的规律。罗俊杰等[18]基于风洞试验结果,利用考虑各方向间脉动分量空间相关性的谐波合成法模型生成三向风荷载时程,对大跨度索屋盖结构进行风振动力响应分析,结果表明不同类型的响应风振系数会有一定差异,一般不能取统一的结构响应风振系数用于结构设计。
目前,大跨索屋盖风振动力响应分析还没有一个明确合理的抗风设计标准和分析计算方法,国内大多基于静力等效风荷载[19-20]进行抗风安全设计,但大跨索屋盖结构振型复杂、多振型参与的原因,等效静力风荷载的计算结果具有一定的不确定性。GB 50009—2012《建筑结构荷载规范》和JGJ/T 4814—2019《屋盖结构风荷载标准》对此类结构风振计算也只给出了简化设计参数[21-22],但难以普及到所有索屋盖结构类型。如何准确合理且行之简单有效的进行风振动力响应分析成为对大跨索屋盖结构亟待解决的关键问题之一。鉴于此,本文针对四类典型大跨索屋盖结构,提出两种风振计算荷载取值模式进行风振动力响应的时程分析,并与传统等效静力风荷载计算结果进行对比,探究索屋盖结构的风致振动特性,提出索屋盖风振动力计算的分析方法,为类似工程抗风分析与设计提供参考和指导。
1 四类典型索屋盖结构
1.1 工程概况
以顺德德胜体育中心和肇庆新区体育中心四类典型索屋盖结构的风振动力响应为研究对象。顺德体育中心主体分为综合体育场、游泳馆、体育馆和训练馆四个部分,总建筑面积达234 458 m2,各部分之间设置结构缝并通过景观连廊、平台等彼此相连,其中顺德德胜体育中心的游泳馆、训练馆和体育馆分别为单层马鞍形索网、轮辐式双层索网、索穹顶大跨索屋盖体系。肇庆新区体育中心主体分为足球场、体育馆和训练馆三个部分,总建筑面积88 000 m2,亦通过景观连廊、平台等彼此相连,本文重点研究的体育馆主馆为弦支穹顶大跨屋盖体系,如图1所示。


图1 四种典型索屋盖结构平面布置与三维效果图Fig.1 Four typical cable roof structure plan layout and three-dimensional renderings
四种典型大跨索屋盖结构的类别和跨度如表1所示,可以看出最大跨度达到了124.3 m,最小跨度也超过了70.0 m。MA采用单层马鞍形索网结构,屋盖平面为椭圆形,索网标高范围为12.9~20.9 m,跨中标高为16.9 m。MA的短向矢跨比为1/17.8,长向矢跨比为1/25.8。支撑体系和抗侧力体系有外围V支撑和屋面环梁共同组成,外围V支撑支撑于下部混凝土柱柱顶上,其截面采用梭形变截面钢柱,屋面环梁采用钢管混凝土梁,索网结构主受力索纵索采用2D80高强密封索,稳定索横索采用2D60高钒索;MB采用双层轮辐式索网,索网标高范围为19.0~24.7 m,支撑体系和抗侧力体系为外围的V支撑、屋面外环梁及内双层压环,索网结构上索采用D100高强密封索,下索采用D110高强密封索;MC采用椭圆抛物面形索穹顶,索网标高范围为27.8~38.4 m,内外圈V柱构成了2两道抗侧力体系,屋盖钢结构结构体系采用了两道环梁,内圈环梁提供拉索绝大部分刚度,外圈环梁为屋面构件封闭环梁,起到二道防线的作用。MC的短向矢跨比为1/13,长向矢跨比为1/15,且整个屋盖系统设有3圈撑杆;MD为弦支穹顶,屋盖的壳体形式为肋环形单层网壳,其支撑体系和抗侧力体系主要由八根巨型Y柱支撑和外围钢管V柱构成。

表1 四种典型索屋盖结构与节点数量Tab.1 Four typical cable roof structure types and the corresponding spans
1.2 风洞试验
德胜体育中心和肇庆新区体育中心的风洞试验均在广东省建筑科学研究院CGB-1实验室完成,所处场地均为B类地貌,根据《建筑结构荷载规范》规定,结构计算风压采用重现期50年10 min平均风速对应的基本风压,德胜体育中心和肇庆新区体育中心的计算风压分别为0.7 kN/m2、0.5 kN/m2。MA-MC的缩尺比均为1∶250,MD的缩尺比为1∶200。德胜体育中心每隔10°分别进行了36组风向角风洞试验测试,肇庆新区体育中心每隔15°分别进行了24组风向角风洞试验测试,如图2所示。

(a) 德胜体育中心

(b) 肇庆新区体育中心
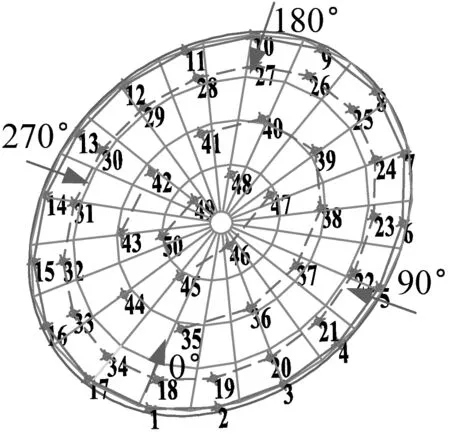
(c) MB测点布置图2 风洞试验模型及模型MB测点布置Fig.2 Wind tunnel test model and measuring point layout of the MB
测试的采样频率均为312.5 Hz,MA-MC的试验风速取对应风洞内0.6 m高处(实际高度150 m)的值,约为10.12 m/s,MD的试验风速取对应风洞内0.6 m高处(实际高度150 m)的值,约为7.46 m/s。从图3中可以看出,顺德德胜体育中心的风洞边界层风速和湍流度剖面沿高度方向的试验值和理论值吻合性良好,试验功率谱密度函数与Kaman功率谱和Davenport功率谱也具有良好的吻合性,表明风洞试验的边界层风特性可以很好的反应实际风场的情况。肇庆新区体育中心的理论与试验结果吻合度也很好,限于篇幅不再赘述。

图3 风洞试验风场模拟Fig.3 Wind field simulation
不同风向角下大跨索屋盖结构风致动力响应存在较大区别,从表2中可以看出,结合MB模型的风洞试验结果,在100°~150°、280°~340°风向角作用下,屋盖的边缘小部分区域出现正风压峰值,最大正风压峰值为0.95 kPa,出现在110°风向角下屋盖边缘区域的6号测点处。在全风向角下屋盖负风压峰值覆盖了整个屋盖,负风压峰值主要集中在0°~80°和310°~350°风向角的屋盖边缘部位,最小负风压峰值达到-2.86 kPa,出现在50°风向角下屋盖边缘区域的3号测点处。根据《屋盖结构风荷载标准》中3.0.6条规定,屋盖结构至少验算分析4个不利风向角下的风效应,因此MB典型的四个不利风向角取0°、50°、110°和330°。限于篇幅原因,同理MA典型的四个不利风向角为120°、210°、290°和350°,MC典型的四个不利风向角为0°、50°、220°和330°,MD典型的四个不利风向角为0°、150°、225°和240°。

表2 MB屋盖各风向角下最大正、负风压位置及大小Tab.2 The maximum negative wind pressure under each wind angle of the MB 单位:kPa
2 屋盖风荷载取值模式
2.1 荷载取值模式
由于大跨索屋盖结构风振响应复杂多变,屋盖节点杆件数量庞大,屋盖控制点不明确、不唯一。等效静力风荷载只能对分区内单个控制点的目标响应进行等效,且不同的目标风振响应等效得到的静风荷载分区也会不同,导致等效静力风荷载计算具有较大的不确定性。为此,本文结合风洞试验时程数据,对大跨索屋盖结构进行动力响应时程分析,基于节点和单元两种动力风荷载施加模式,提出节点动力风荷载和面组分区动力风荷载两种荷载取值模式。同时,为与现有计算方法进行对比,依据GB 50009—2012《建筑结构荷载规范》中定义的风荷载标准值计算相应的等效静力风荷载。
大跨索屋盖结构和高层建筑不同,风时程只能对每个节点或者面进行加载。风洞试验得到的只是有限的测点风压系数时程,结构的节点远比测点数量多,这就要对结构所有节点进行风压插值。本文采用最近邻点插值方法进行风压插值,插值函数L如下
(1)
式中:Cix、Ciy、Ciz分别为测点i的X向、Y向、Z向的坐标;Jjx、Jjy、Jjz为结构节点j的坐标;L为插值函数值;方差0.01的功能是为了避免风洞试验测点和结构节点完全重合而出现计算错误。
通过式(1),每个结构节点遍历所有风洞试验测点进行计算,当L最小时,将第i个测点的风压系数时程赋予第j个受风节点。本研究使用MATLAB软件编辑了插值函数L,获得结构节点与风洞试验测点间的对应关系,即风压插值矩阵[D]
[J]=[C][D]
(2)
式中:[J]为结构所有节点几何坐标分布矩阵;[C]为结构所有风洞测点几何坐标分布矩阵。
由此可得结构节点与风洞试验测点风压系数时程之间的转化关系
(3)
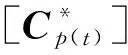
(4)
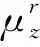

(5)
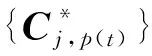
(6)
等效静力风荷载取值模式是根据风振时程分析的结果以及结果自振特性对结构进行分区,根据分区内风位移效应最值得到结构分区位移风振系数βz,根据结构体型以及风洞试验结果分析得到的面组分区体型系数μs,最后参照建筑结构荷载规范中风荷载定义计算得出所有面组分区的等效静力风荷载,如式(7)所示
wk=βzμsμzω0
(7)
式中:μs为体型系数;μz为风压高度变化系数;βz为风振系数,计算公式如下
(8)

(9)
式中:u(t)为结构节点位移时程;N为总样本点数。
图4总结了上述三种风荷载取值模式及结构风致响应分析计算流程图。

图4 三种风荷载取值模式及结构风振响应Fig.4 Three modes of wind load and wind-induced response of structures
2.2 最近邻点插值方法验证
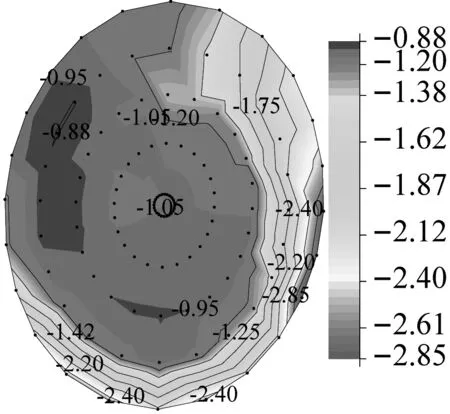
以MB、MC两种大跨索屋盖进行风压插值的结果,进行最近邻点插值方法[23]的合理性验证。MB屋盖共120个节点,风洞试验测点50个;MC屋盖共331个节点,风洞试验测点124个。图5为屋盖全风向角下风压峰值分布云图,从图5可以看出,最近邻点插值方法得到的结构风压峰值分布云图与风洞试验结果具有良好的吻合度,分布轮廓合理流畅,进而可验证基于该方法进行风洞试验测点风压与原结构节点风压之间转换的合理性。

(a) MB-风洞试验
(b) MB-最近邻点插值法

(c) MC-风洞试验

(d) MC-最近邻点插值法图5 屋盖全风向角下风压峰值分布云图(kPa)Fig.5 Cloud atlas of peak wind pressure distribution under full wind direction angle of roof(kPa)
3 计算结果分析
结合所提节点动力风荷载和面组分区动力风荷载两种动力荷载取值模式,计算得到有限元模型各个节点、面组分区上的动力风荷载时程,然后基于MIDAS软件平台,采用Newmark-β法对四类典型索屋盖结构进行动力非线性时程分析,持时600 s。通过风洞试验与实际结构之间的几何缩尺比和风速比,换算得到50年重现期下10 min风振分析时间步长。顺德德胜体育中心B类地貌风洞试验实际参考高度(50.65 m)处对应的实际风速为42.66 m/s,对应的试验风速为8.60 m/s,由此计算可得MA~MC模型分析时间步长为0.161 2 s,同理MD模型的分析时间步长为0.136 8 s。同时,不同风向作用下结构动力响应也存在一定的区别,结合风洞试验结果选取四种不利风向角的风荷载进行动力响应对比分析。为便于阅读,图6给出了MA~MD模型的面组分区及典型节点编号,典型节点均位于索屋盖结构风振动力响应显著的区域。



图6 MA~MD模型面组分区与典型节点Fig.6 Surface component region and typical nodes of MA-MD
MA~MD模型中采用了非线性索单元,即施加了预拉应力,索不会受压。采用非线性时程分析方法进行索屋盖结构风振响应分析时,结构风振响应实际为非线性风振动力响应。
3.1 结构动力特性
此外,在工程设计中广泛使用Rayleigh阻尼计算阻尼矩阵,目前大多数结构在设计分析时[ωi:ωj]仅采用前两阶,这对于频率分布密集的索屋盖结构是不适用的。在频段[ωi:ωj]外,其计算的阻尼将迅速增大,频段外的振动会被抑制,距离频段越远的部分计算结果将远小于实际值,甚至可以忽略不计,但如果有频段外存在对结构设计十分重要的频率分量,会对计算结果产生较大的影响,使得结构设计偏于不安全。故在分析时应覆盖索屋盖结构振型贡献较大的所有频段。为此通过4个模型在不同频段范围内对分析结果的精确性分析,对四类模型在不同的频段[ωi:ωj]进行时程分析,对其典型节点处的结果进行对比分析,找出趋向某个频段时,风振位移结果偏差较小,即覆盖了索屋盖结构分析中关键的频段[ωi:ωj]。
从图7中可以看出,前5阶、前10阶、前20阶和前50阶的计算结果非常接近,且覆盖了屋盖结构分析中感兴趣的频段,较为合理,MB模型采用前20阶频段[3.622,6.460] Hz,计算结构具有较高的保证率。因此经计算分析,进行时程动力分析MA~MD在时程分析时频段的可依次取前5阶、前20阶、前20阶和前5阶振型。
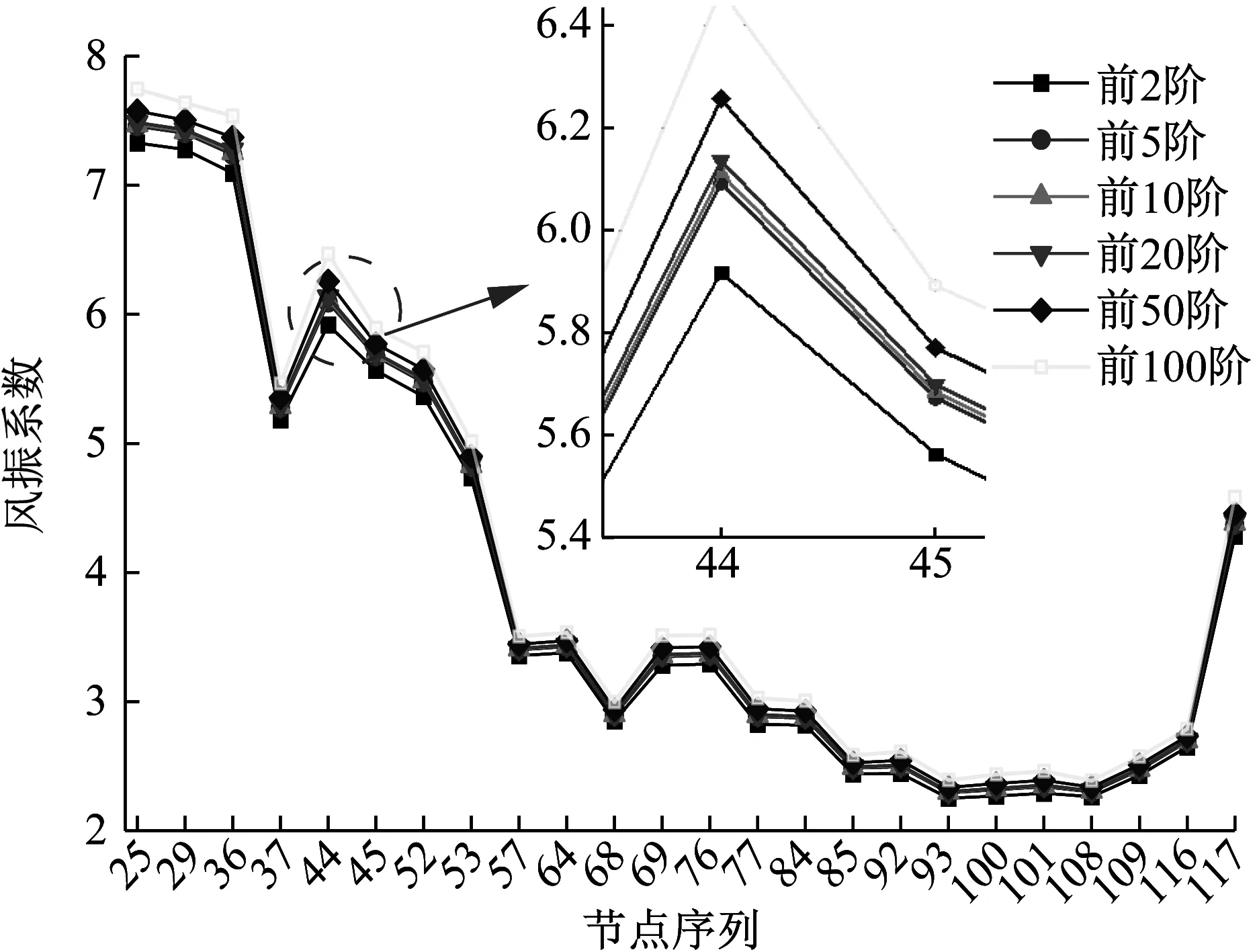
图7 不同振型频段下MB屋面节点序列风振系数Fig.7 Wind vibration coefficient of MB roof node sequence under different vibration mode frequency bands
图8给出了四种典型索屋盖结构的频率随振型的变化曲线和典型竖向振型云图,振型数根据振型参与质量累计达90%确定,其中MA模型和MB模型须达到前200阶振型、MC模型为前90阶振型、MD模型为前30阶振型。可以看出,大跨索屋盖结构具有频率密集的自振特性,自振频率较小,如MA模型前100阶频率均密集在2.33~7.79 Hz之间,MB模型前100阶频率均密集在0.58~2.26 Hz之间,MC模型前50阶频率均密集在0.48~2.84 Hz之间,MD模型前20阶频率均密集在1.01~3.25 Hz之间。索屋盖以Z向振动为主,下凹型MA模型第一阶振型在中间部位发生竖向变形(如图8(a)所示);上凸型MB~MD模型一阶振型与下凹型模型有一定的区别,呈现沿屋盖中心区域分两侧振动(MB、MD模型,如图8(b)、(d)所示)和环绕振动(MC模型,如图8(c)所示)两种竖向振动模式,主要与屋盖的结构形式有关。此外,高阶振型虽伴随一定的水平和扭转耦合振动模式,如MC模型第10阶和MD模型第5阶Z向振动同时伴随水平、扭转振动,但整体上后两种振型模式的贡献不大。可见,大跨索屋盖结构的风振动力响应分析中应重点关注屋面的Z向振动响应。

(a) 模型MA

(b) 模型MB

(c) 模型MC

(d) 模型MD图8 MA~MD模型动力特性Fig.8 Dynamic characteristics of the models MA-MD
3.2 结构动力响应分析
3.2.1 三种荷载取值模式对比分析
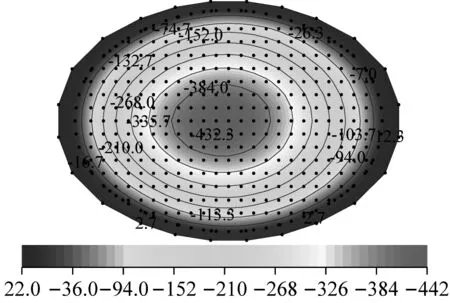
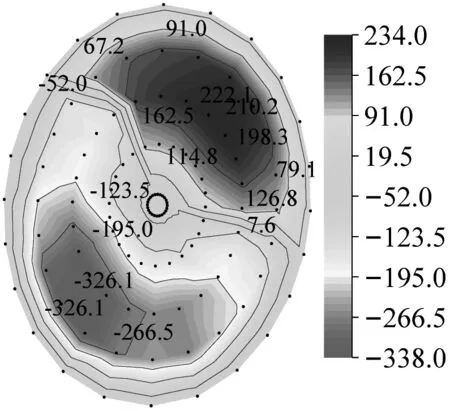
图9给出了两种模式下MA~MD模型屋盖所有节点Z向风振总极值位移云图,图10中给出了所提出的两种荷载取值计算模式和传统的等效静力风荷载计算模式下的屋盖节点风振总极值位移响应对比。定义负总极值位移响应为屋盖中节点的风振总极值位移响应为负,正总极值位移响应为屋盖中节点的风振总极值位移响应为正,最小负总极值位移响应为屋盖所有节点总极值位移响应为负值中的最小值。从图中可见,基于节点的动力风荷载取值计算模式(模式一)与基于面组分区的动力风荷载取值计算模式(模式二)得到的屋盖风振极值位移云图总体分布规律较为一致,风振负总极值位移响应较为相近,如MA模型最小负总极值分别为-442.00 mm和-414.00 mm、MD模型最小负总极值分别为-64.20 mm和-65.00 mm,MA、MB、MD模型最小负总极值响应的差异依次为-28.00 mm、12.00 mm和0.80 mm。然而,MC模型基于模式一和模式二得到的最小负总位移极值差异过大,达到-221.50 mm,主要原因在于同一面组分区内不同节点的风荷载差异过大,而面组分区采用基于分区内节点荷载平均的计算方法,导致平均后该面组分区的风荷载降低而使得位移响应也随之降低。同时,由于面组分区内对所有节点取均值的原因,亦有可能造成某些分区中部分节点所承担的风荷载增大而造成响应上升的现象,如图10中MB模型最大正总极值位移模式一和模式二分别为226.00 mm和234.00 mm,后者较前者高8.00 mm。
(a) MA-210°-模式一

(b) MB-330°-模式一

(c) MC-330°-模式一
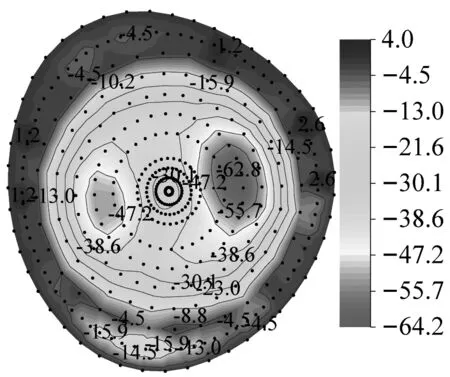
(d) MD-0°-模式一

(e) MA-210°-模式二
(f) MB-330°-模式二

(g) MC-330°-模式二

(h) MD-0°-模式二图9 MA~MD模型屋盖节点Z向风振极值位移云图(mm)Fig.9 The Z-direction extreme displacement contours of the MA-MD model roof(mm)

(a) MA~MD最大正极值位移对比
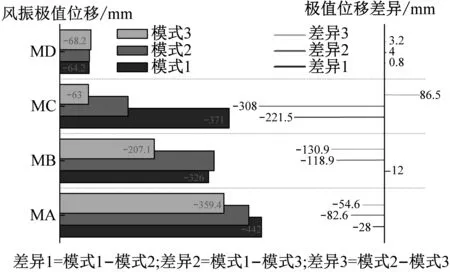
(b) MA~MD最小负极值位移对比图10 MA~MD模型屋盖节点风振极值位移对比Fig.10 Comparison of wind vibration of extreme displacement of MA-MD
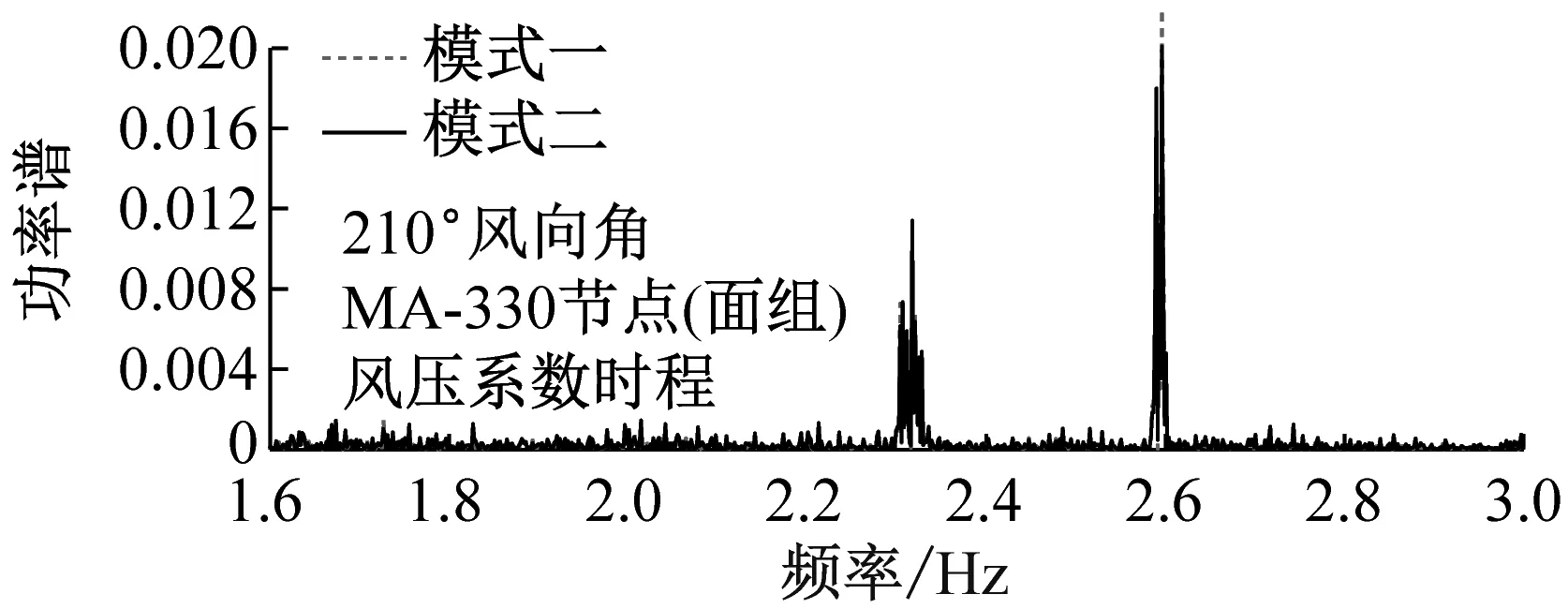
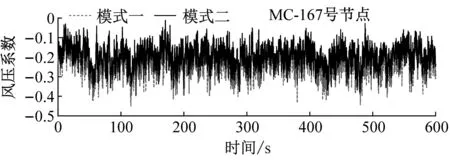
进一步,从时程曲线及功率谱密度函数的对比上亦可看出经平均后两种模式亦存在一定的差别,如图11所示。MA、MC、MD模型在210°、330°、0°风向角下,Z向风振位移响应最大处对应的330号、167号、89号节点的Z向风振总极值位移响应分别为-442.00 mm、-371.00 mm、-64.20 mm(模式一)和-359.39 mm、-149.50 mm、-65.00 mm(模式二),对应地模式一与模式二的差异依次为-28.00 mm、-221.50 mm、0.80 mm。从功率谱密度上也可以看出,经面组分区内的节点风压系数平均后,两种模式的功率谱密度也相应产生了一定的差异,尤其是对于前述分析响应差别很大的MC模型,其风压系数的功率谱密度同样存在很大的区别(如图11(d)所示),显然输入风荷载的较大差异将直接导致结构动力响应的显著差别。

(a) MA模型最大Z向位移节点的风压系数时程
(b) MA模型最大Z向位移节点的风压系数功率谱
(c) MC模型最大Z向位移节点的风压系数时程

(d) MC模型最大Z向位移节点的风压系数功率谱

(e) MD模型最大Z向位移节点的风压系数时程

(f) MD模型最大Z向位移节点的风压系数功率谱图11 MA/MC/MD模型最大Z向位移节点处风压系数时程与功率谱Fig.11 Time series and power spectrum of pressure coefficient at key node with maximum Z-displacement of MA/MC/MD models
表3进一步给出了其他代表性不利风向角作用下基于两种荷载取值模式下的四个模型最大绝对负极值位移对比,可见二者仍然存在一定的差别,且仍以MC模型的差异最大,最大相差315.26 mm,MD模型差异最小为0.44 mm。因此,可以说明模式一采用节点风荷载取值计算模式,将风洞试验数据直接通过最近邻点插值方法转化到结构模型的节点上,该动力风荷载取值模式能够反映屋盖结构实际承担的风荷载,以此计算得到的结构风振响应可有效表征屋盖结构在风振激励下的动力效应。
相比而言,模式三与模式一、模式二的计算结果存在较大的差异,如模式三与模式一对比四组模型最小负总极值响应的差异依次为-82.61 mm、-118.91 mm、-308.00 mm和4.00 mm,模式三与模式二对比相应的差异依次为-54.61 mm、-130.91 mm、86.50 mm和3.20 mm,且模式三的风振响应计算结果均偏小(绝对值),说明基于传统等效静力风荷载得到的屋盖结构风振效应低估了实际风致振动响应,计算结果偏于不安全。依据JGJ 257—2012《索结构技术规程》及GB 50017—2017《钢结构设计标准》[24-25]中的相关规定,MA、MC和MD设计时允许最大挠度与跨度之比不宜大于L/250,MB设计时允许最大挠度与跨度之比不宜大于L/200。从表3亦可以看出,MA在210°风向角下、MB在50°风向角下以及MC在50°风向角下的屋盖风振极值位移响应峰值超过了屋盖挠度限值,且均再上下游无临近场馆的风向角下,表明索屋盖在无临近建筑的风向角下会存在最不利风振极值位移响应,由此建议应采用基于动力时程分析的方法计算大跨索屋盖结构的风致振动响应。
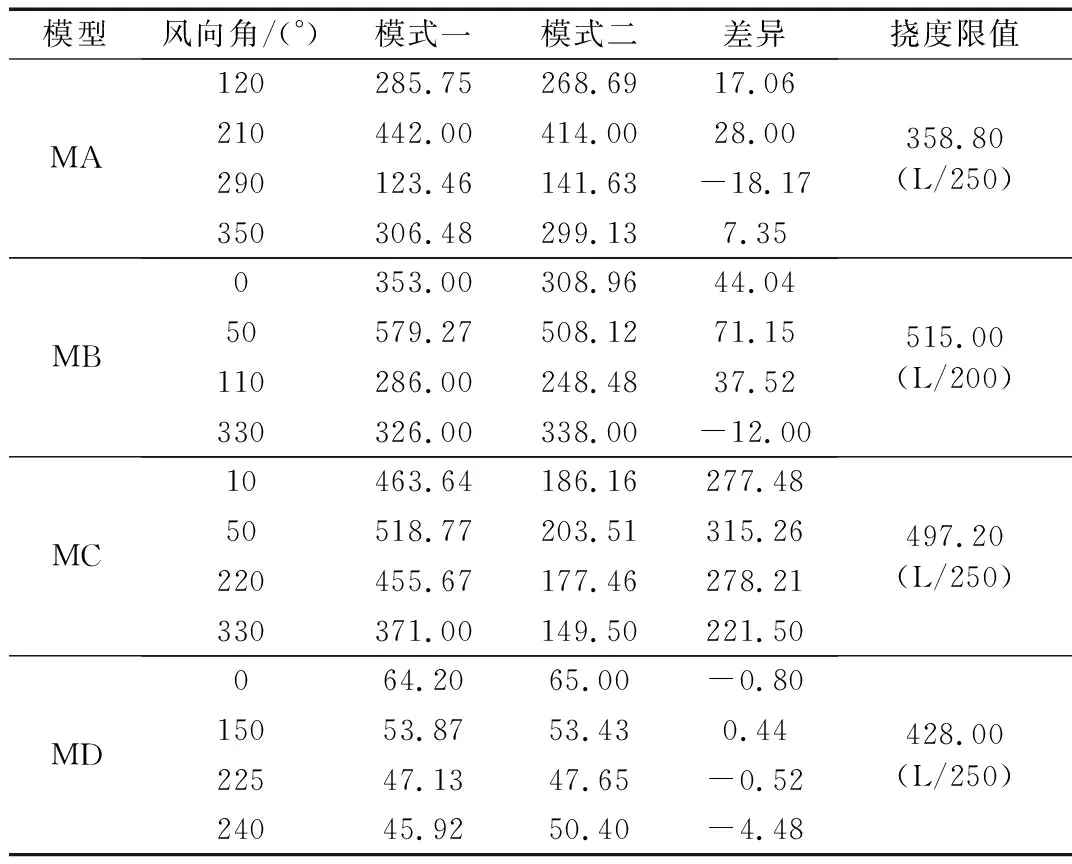
表3 典型风向角下MA~MD模型屋盖Z向最大绝对负总极值位移响应 单位:mmTab.3 Maximum absolute negative Z-direction displacement of MA-MD model under typical wind directions
值得一提的是,虽然在三种荷载取值模式下四组模型最大正极值的计算结果均存在较大差异,如图10中MA~MD模型最大正极值差异3依次为16.92 mm、206.52 mm、1.13 mm和6.45 mm,但相比负极值而言,屋盖位移正极值普遍都很小,如MB模型正、负总极值位移的绝对值分别为22.00 mm、442.00 mm(模式一),MD模型正、负总极值位移的绝对值分别为20.20 mm、65.00 mm(模式二)。对于正极值较大的MB模型,亦有类似结论,其正、负总极值位移的绝对值分别为226.00 mm和326.00 mm(模式一),后者仍为前者的1.44倍。可见,实际工程设计中屋盖结构可主要以风振负位移极值作为设计控制指标,对于正位移极值可不予重点关注。
3.2.2 风致振动响应与风振系数分析
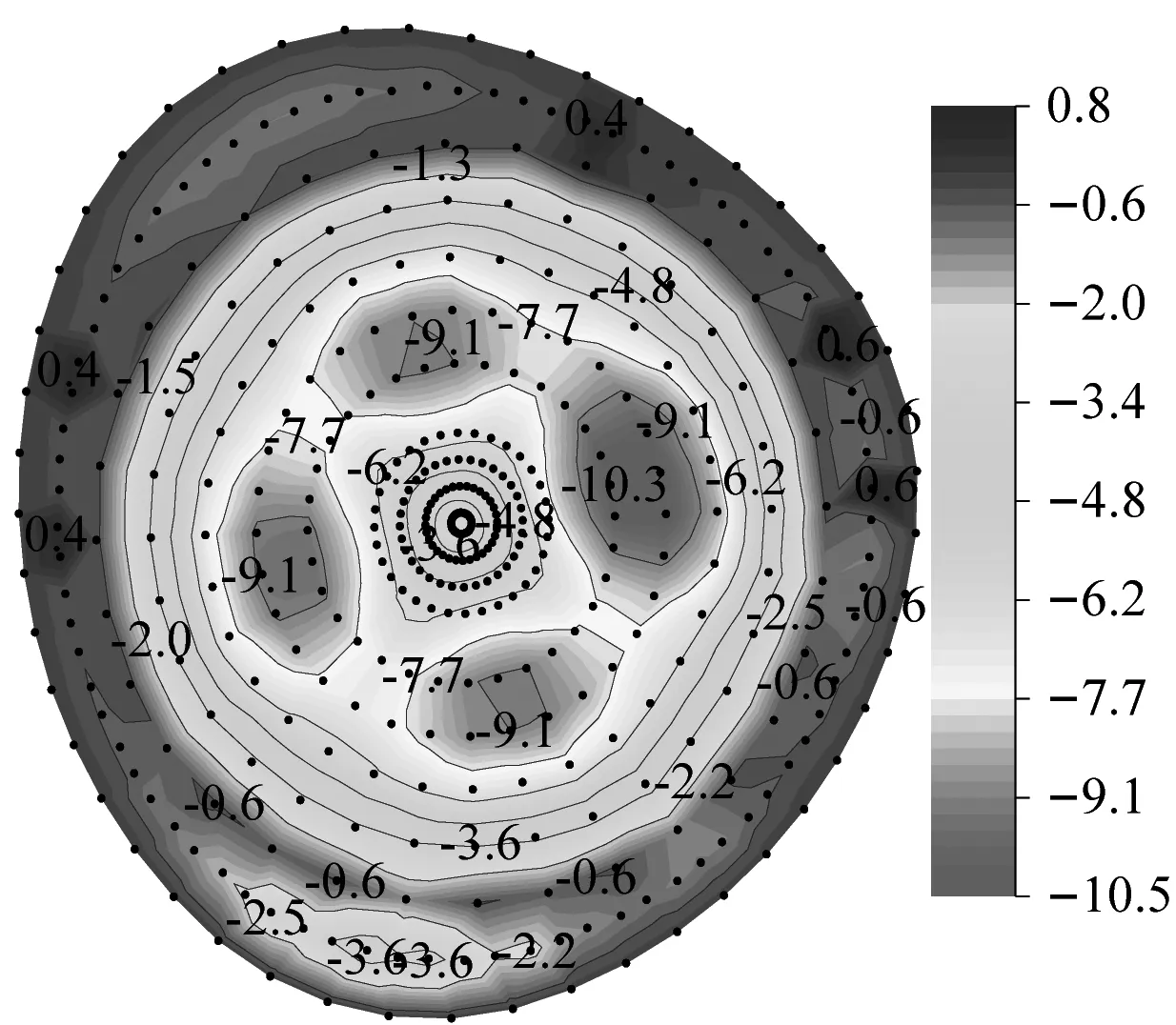
图12给出了采用模式一节点动力风荷载输入条件下,MA~MD模型屋盖Z向风振位移响应(mm)与风振系数云图。可以看出,在210°风向角下(上下游无临近场馆),下凹型索屋盖MA模型平均和脉动风作用下的位移响应具有一致的分布特性,呈现中间大、周边小的逐渐递减的规律,平均风作用下的位移响应较脉动风下的响应大;屋盖风振系数绝大部分区域稳定在1.8左右,仅边缘个别区域超过4.0。对于上凸型MC、MD模型屋盖,两个风向角下同样属于上下游无临近场馆影响的条件,平均和脉动风作用下的位移响应虽同样具有较为一致的分布特性,但位移响应的变化规律与下凹型存在一定的区别,呈现屋盖中心区域小、中间环带大、周边再次下降的变化规律,表明上凸型屋盖在中间环带处承担了较大的风荷载,并向环带两侧分流,产生较大的脉动风振作用;上凸型屋盖的风振系数大部分区域处在1.7~4.0范围内,但同样在边缘区域产生了显著的风振系数,甚至超过8.0。
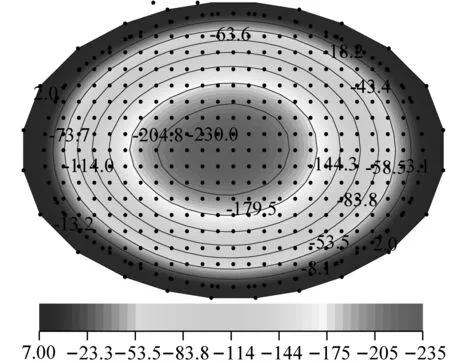
(a) MA-平均风响应

(b) MA-脉动风响应
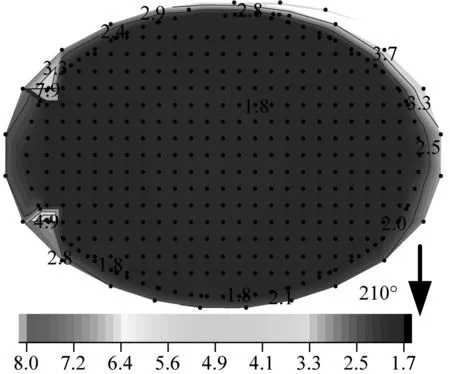
(c) MA-风振系数
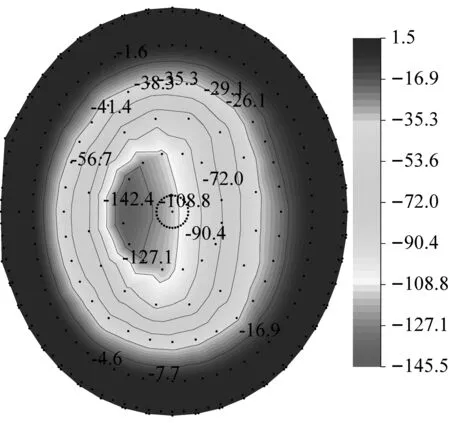
(d) MC-平均风响应

(e) MC-脉动风响应

(f) MC-风振系数

(g) MD-平均风响应
(h) MD-脉动风响应
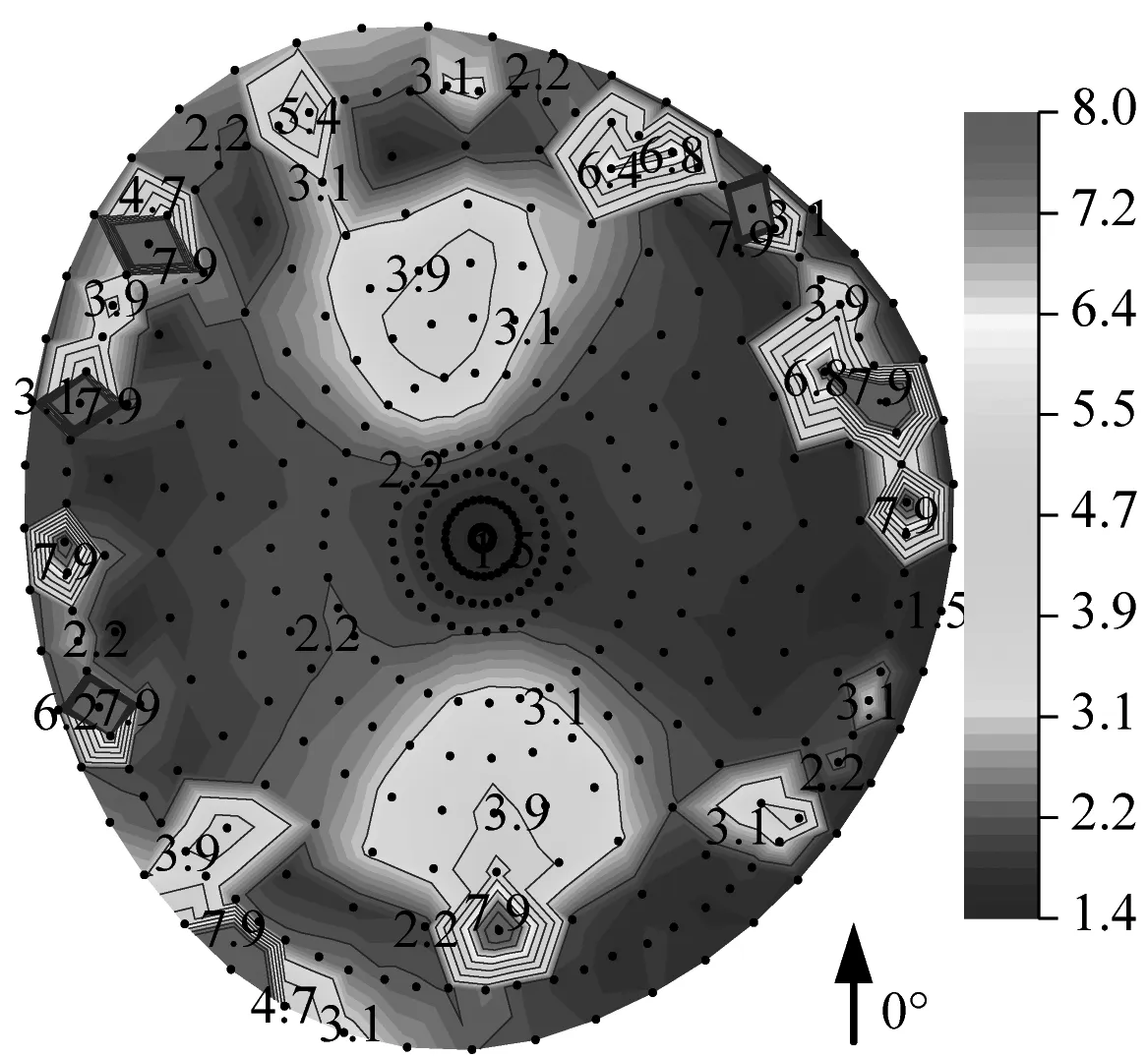
(i) MD-风振系数图12 模式一条件下MA~MD模型屋盖Z向风振位移响应与风振系数(mm)Fig.12 Z-direction wind-induced displacement response nephogram of MA-MD roof under node dynamic wind load mode(mm)
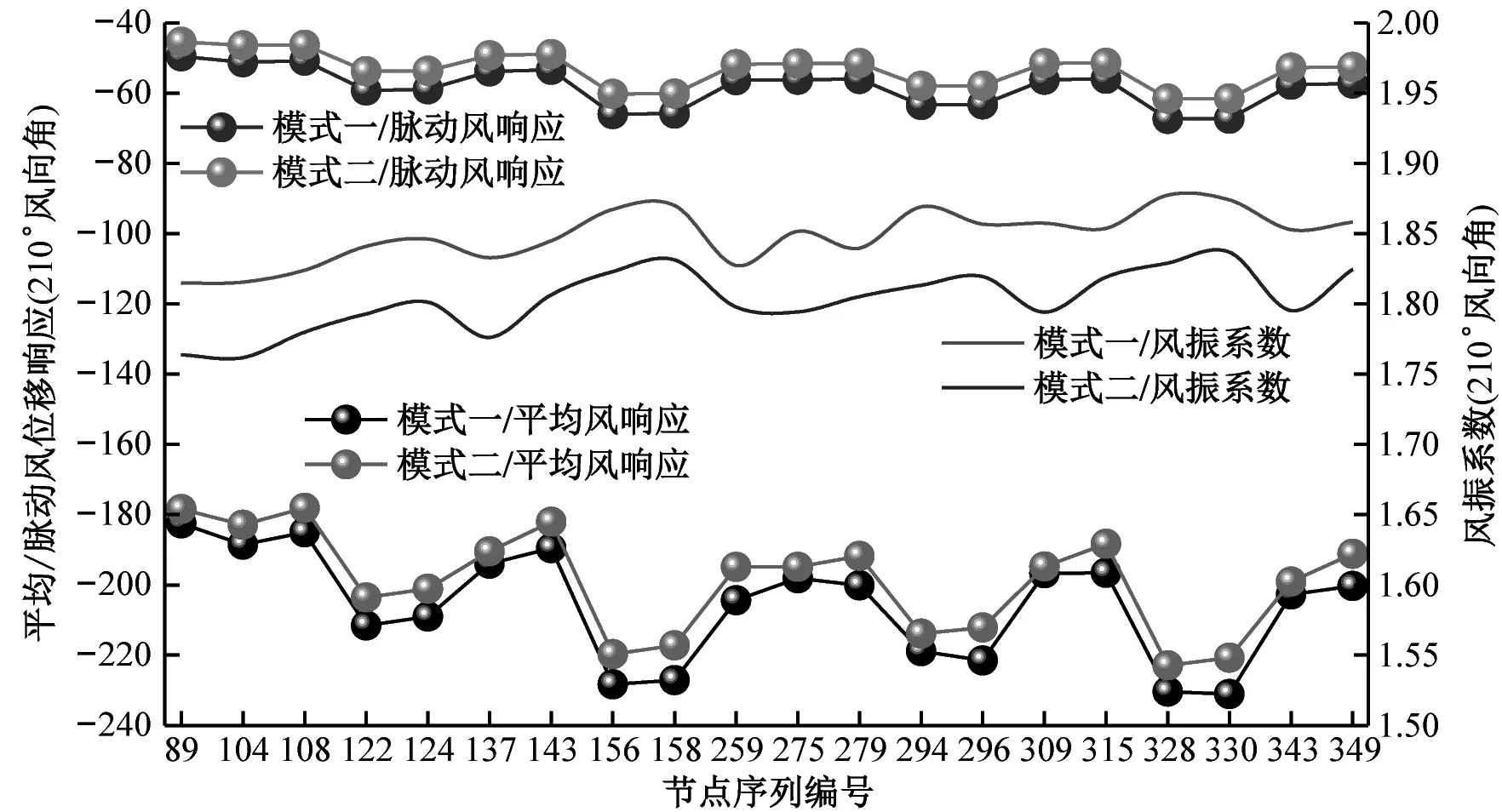
为进一步探究平均、脉动风振位移响应与风振系数之间的关系,选取四个屋盖的代表性风振响应较大的测点序列,绘制两种荷载模式下MA~MD模型典型节点序列的风振位移响应与风振系数变化曲线,如图13所示。可见,屋盖不同区域节点风振系数差异较大,当平均风位移响应比脉动风响应大、且不接近于0时,风振系数一般介于1.70~4.00;当平均风位移响应比脉动风响应小、且不接近于0时,风振系数一般介于4.00~8.00;当平均风响应接近于0或者远小于脉动风响应时,风振系数均高于8.00,甚至出现奇异突变点,如图13(b)模型MB节点45和节点84,风振系数分别达到27和32,从风振系数定义式(8)可知,其主要原因在于这些测点的平均风响应过小而导致。索屋盖结构抗风设计过程中,如果按照《建筑结构荷载规范》中的方法,即用平均风位移很小节点处的风振系数去计算等效静风荷载,等效静风荷载会远超结构实际所受的风荷载值。因此索屋盖结构抗风设计时宜采用风振动力响应时程分析,得到的结构风振响应更为准确。
(a) MA模型

(b) MB模型

(c) MC模型

(d) MD模型图13 MA~MD模型典型节点序列风振位移响应与风振系数Fig.13 Wind-induced displacement response and gust response coefficient of MA-MD Typical Node Sequence
此外从图中还可以看出,两种风荷载取值模型下屋盖平均/脉动风致响应及其风振系数均存在一定的差异,总体表现出模式一基于节点荷载取值模式下风致响应高于模式二(基于面组分区荷载取值模式)。
4 结 论
以MA~MD四类典型大跨索屋盖结构为研究对象,对比分析了三种荷载取值模式激励下结构的风致振动响应,取得结论如下:
(1) 结合风洞试验测试数据和最邻点插值方法,提出了索屋盖结构基于节点动力风荷载和面组分区动力风荷载两种荷载取值计算模式,给出了计算流程图。
(2) 两种动力风荷载作用下索屋盖风振极值位移云图总体分布规律较为一致,但极值响应大小存在一定的差别,模式一采用节点风荷载取值计算模式能够更为精确地反映屋盖结构实际承担的风荷载,有效表征屋盖风致振动响应。
(3) 模式三采用传统等效静力风荷载的取值模式,其屋盖风致振动响应均较模式一、模式二偏低,相比模式一和模式二,采用模式三计算的四类结构负极值响应最大偏低分别为308.00 mm和221.50 mm,低估了屋盖结构的实际风致振动响应,计算结果偏于不安全。
(4) 在上下游均无临近场馆影响下,下凹型和上凸型索屋盖平均和脉动风振位移响应云图均具有一致的分布特性,但响应大小变化规律不一,下凹型呈现中间大、周边小的逐渐递减的规律,而上凸型屋盖呈现中心区域小、中间环带大、周边再次下降的变化规律。
(5) 屋盖不同区域风振系数差异较大,当平均风位移响应比脉动风响应大、且不接近于0时,风振系数一般介于1.70~4.00;当平均风位移响应比脉动风响应小、且不接近于0时,风振系数一般介于4.00~8.00;当平均风响应接近于0或者远小于脉动风响应时,风振系数均高于8.00,甚至出现奇异突变点。索屋盖结构抗风设计时宜采用风振动力响应时程分析,得到的结构风振响应更为准确。

