基于PSASP 的新能源恒频控制策略建模与仿真分析

徐 东，李兆伟，朱 玲，吴雪莲，林文莉，李天然

（1.南京师范大学南瑞电气与自动化学院，江苏 南京 210042；2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏南京 211106；3.国电南瑞科技股份有限公司，江苏南京 211106；4.华北电力大学 电气与电子工程学院，北京 102206）

近年来，我国新能源的装机容量已居于世界首位。预计至2035 年，我国新能源装机容量将超过传统发电的装机容量[1]。新能源发电占比快速增加，使得电力系统的整体惯量水平和调节能力大幅下降，系统发生较小故障也会引发频率产生较大的偏差[2-5]。

基于电力电子技术的新能源发电具备良好的频率调节潜力。有学者甚至认为电力系统可以实现100%的电力电子化新能源发电[6-7]。根据响应电网频率变化的方式不同，可以通过下垂控制、虚拟惯量控制或恒定功率控制等调整新能源发电功率[8-12]。我国于2019 年发布的《电力系统安全稳定导则》[13]明确规定包括新能源在内的所有电源均应具备一次调频能力，2021 年发布的《风电场接入电力系统技术规定》[14]对陆上风电的一次调频和惯量响应提出了量化要求，其中一次调频采用下垂控制，惯量响应则根据电网频率变化率调节新能源发电输出功率。此外，基于电网构造型（GFM）变流器的频率控制方法近年来也被相继提出[15-18]，但其对大电网稳定特性的影响还缺少系统研究。

该文针对新能源恒频控制（Constant Frequency Controlled New Energy，CFCNE）这一频率主动支撑方式，建立其数学模型，基于PSASP 用户自定义（UD）环境搭建了完整的恒频控制仿真模型，并通过典型IEEE 系统仿真验证了交直流故障下恒频控制的响应特性。

1 新能源恒频控制简介

CFCNE 是一种基于GMF 变流器实现的频率主动支撑策略，和虚拟同步机控制类似，适用于无传统同步发电机的电网，这一点与采用下垂控制、虚拟惯量控制的新能源发电不同。因此，理论上恒频控制面向于高比例新能源接入的电力系统，甚至全新能源接入的电力系统，从而使变流器可以充分发挥其电力电子器件具有的快速控制能力，维持系统频率保持恒定。

恒频控制总体控制框图如图1 所示[19]，包含有功控制、无功控制、频率采集三个部分。恒频控制输出的电压幅值Vt参与无功功率。频率采集模块提供恒频控制输出的频率Δω给有功控制环，有功控制环计算出与机端电压相角等效的虚拟相角δ，该相角与系统设定的参考相角δ0进行比较，附加一定的增益后输出参考的有功功率Pcmd，该有功控制方式避免了对频率的直接控制，进一步对相角进行控制，可以实现系统发生功率扰动后无差频率调节，故称为恒频控制。图中Vtd、Vtq为机端输出的d轴电压和q轴电压，θ为发电机机端相角，Pref和Qref分别为输入有功功率和无功功率参考值。

图1 恒频控制总体控制框图

该文不考虑CFCNE 的能量来源问题，假设CFCNE 的能量来源无穷；忽略交直流故障扰动后新能源控制策略切换过程，即假设电力电子器件的容量大到足够承受电网各种短路故障，该文主要针对恒频控制策略在PSASP 用户自定义模型中搭建模型原理和恒频控制本身所呈现的特征进行研究。

2 基于PSASP平台的恒频控制建模

PSASP 是目前应用较为广泛的电力系统机电暂态仿真工具，主要用于对大电网的机电暂态特性进行仿真，其内置的用户自定义暂态模型建模可以帮助使用者在不了解平台内部软件设计结构和仿真运行程序编程的前提下，按照自己所需的控制逻辑，运用基本的函数逻辑和控制逻辑框，搭建可以与PSASP 内固有的系统元件进行交互仿真的控制模型。基于PSASP 平台开展CFCNE 建模，便于开展大量采用恒频控制的新能源接入大电网的安全稳定特性分析，基于PSASP 平台的恒频控制模型的总体结构图如图2 所示。

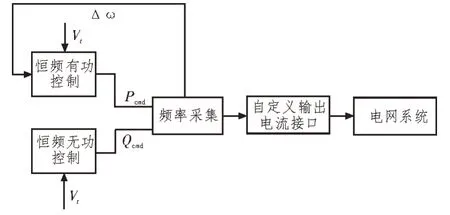
图2 恒频控制结构图

恒频控制暂态稳定自定义模型主要由恒频有功控制模块、恒频无功控制模块、频率采集模块、自定义输出电流接口模块共四个模块组成，频率采集模块负责为有功控制环节和无功控制环节提供频率和电压，有功无功控制模块输出参考的有功功率和无功功率，自定义输出电流接口负责完成dq轴电流的计算和与PSASP 的交互。

2.1 恒频控制有功控制模块

CFCNE 接入电网示意图如图3 所示。

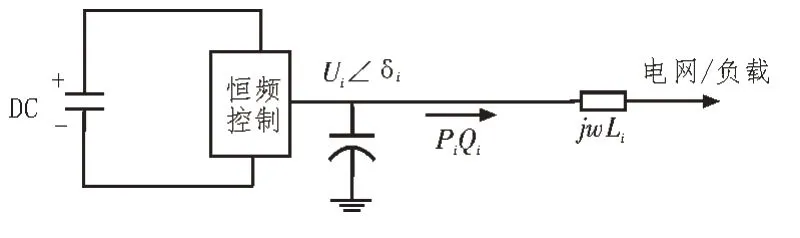
图3 CFCNE与电网连接示意图

不同于微网，大电网环境下逆变器输出阻抗一般是呈现感性的，故忽略电阻，仅用jωLi表示电感。设第i个逆变器向电力系统输入的复功率功率为Si，则有：

δi为CFCNE 输出端与并网点的功角差，第i个恒频控制的有功功率和无功功率为：

考虑到感性电路中δi很小，所以有sinδi≈δi，cosδi≈1。则恒频控制输出的有功功率P的大小可以通过其相角差δi来调节，而无功功率Q的大小可由电压幅值U来调节。从而可以得到恒频有功控制公式：

恒频有功控制基于对频率偏差Δω积分出的相角偏差进行控制，相当于在有功控制环内增加了积分控制环节，避免了传统频率下垂控制所产生的频率偏差，可以实现系统频率无差调节。Kδreff为恒频控制有功控制环节的增益，其控制原理框图如图4 所示。

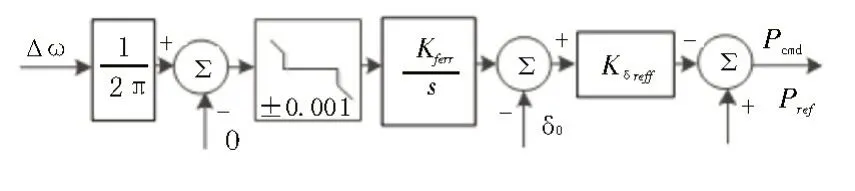
图4 恒频控制有功原理框图

2.2 恒频控制无功控制模块

无功控制环表示式如下：

由式（7）可得：

恒频控制电压-无功控制环节加入了PI 控制，提升了无功控制环的响应速度，消除了静差。

2.3 频率采集模块

基于同步坐标系锁相环（Synchronous Rotating Frame Phase-Locked Loop，SRF-PLL）是最典型和常用的锁相环，根据典型锁相环控制原理建立机电暂态模型。

设恒频控制输出端电压瞬时值可表示为:

进行CLARK 变换有：

对CLARK 变换后的值PARK 变换可得:

将式（11）代入式（12）可得:

由于α≈θ，有:

上式为SF-PLL 的机电仿真下的数学模型，通过该式即可将锁相环由三相瞬时值表达转化为基于机电暂态的等效表达。

2.4 自定义电流接口模块

PSASP 用户自定义平台提供了固定的电流接口用于用户编写的模型接入仿真平台，故在控制后需要将控制所产生的电流量与平台所提供的电流接口量进行转换，完成自定义模型与仿真平台的交互。

自定义电流接口模块主要完成PSASP 系统仿真数据与PSASP/UD 用户自定义暂态发电单元模型数据的交互。该模块主要分为三部分计算：第一部分完成初始状态计算。在PSASP 内对系统进行仿真时需要保证自定义模型的各个输出变量的初态（0+时刻）与系统稳定状态下潮流计算的解相同，若两者不同会导致系统失稳或仿真无法运行。第二部分为dq轴坐标系参考电流计算模块，该模块主要将控制产生的功率量转换为电流量。PSASP 在暂态仿真时提供在αβ坐标系下的母线正序电流的实部和虚部作为PSASP/UD 自定义模型输出接口，故需要第三部分将dq轴电流转换到αβ轴。初值计算公式如下：

式中，PC0、QC0为稳态潮流计算所得的有功和无功解；VT0为自定义发电机接入端母线电压初始幅值；θ0为自定义发电机接入端母线电压初始相角；Iα0、Iβ0为算得的初始电流实部和虚部。

dq轴坐标系参考电流计算公式如下：

式中，Pcmd、Qcmd为控制输出的参考有功、无功；Vtd、Vtq为dq轴下母线的d轴电压和q轴电压；Id、Iq为dq轴下母线的d轴电流和q轴电流。

dq轴电流以母线电压的q轴为y轴，以母线电压的d轴为x轴。在PSASP中不提供dq轴电流直接接入系统，需要进行坐标变换。在PSASP中以母线电流的α轴为x轴，以β轴为y轴。由于dq轴的电压实部与αβ轴电流实部之间相差一个电压与电流夹角θ，故需要将dq轴电流旋转θ度接入仿真系统。其关系如图5所示。

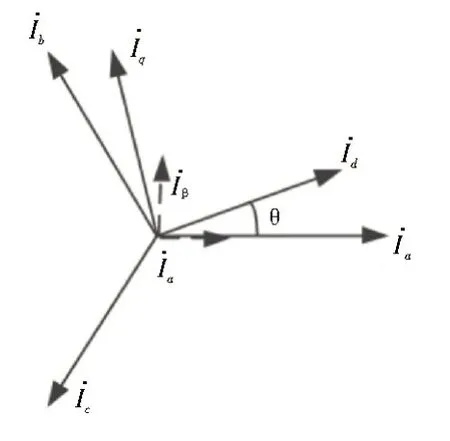
图5 不同坐标系下电流关系图

电流转换公式如下：

式中，Iα、Iβ为αβ轴下母线的α轴电流和β轴电流，θ为电压相角。

初值计算部分确保0+时刻系统初值与恒频控制输出初值相同，保证系统可以正常运行。通过前文所述控制环节输出的有功功率和无功功率参考值求得控制电流，控制电流转换到αβ轴后便完成了恒频控制模型与PSASP 仿真平台的数据交互。

3 仿真分析

仿真采用三机九节点系统，如图6 所示，发电机2 代表CFCNE 场站，发电机1、3 为常规同步发电机群，CFCNE 场站和同步发电机群由一台等值机近似。表1 为系统主要参数。

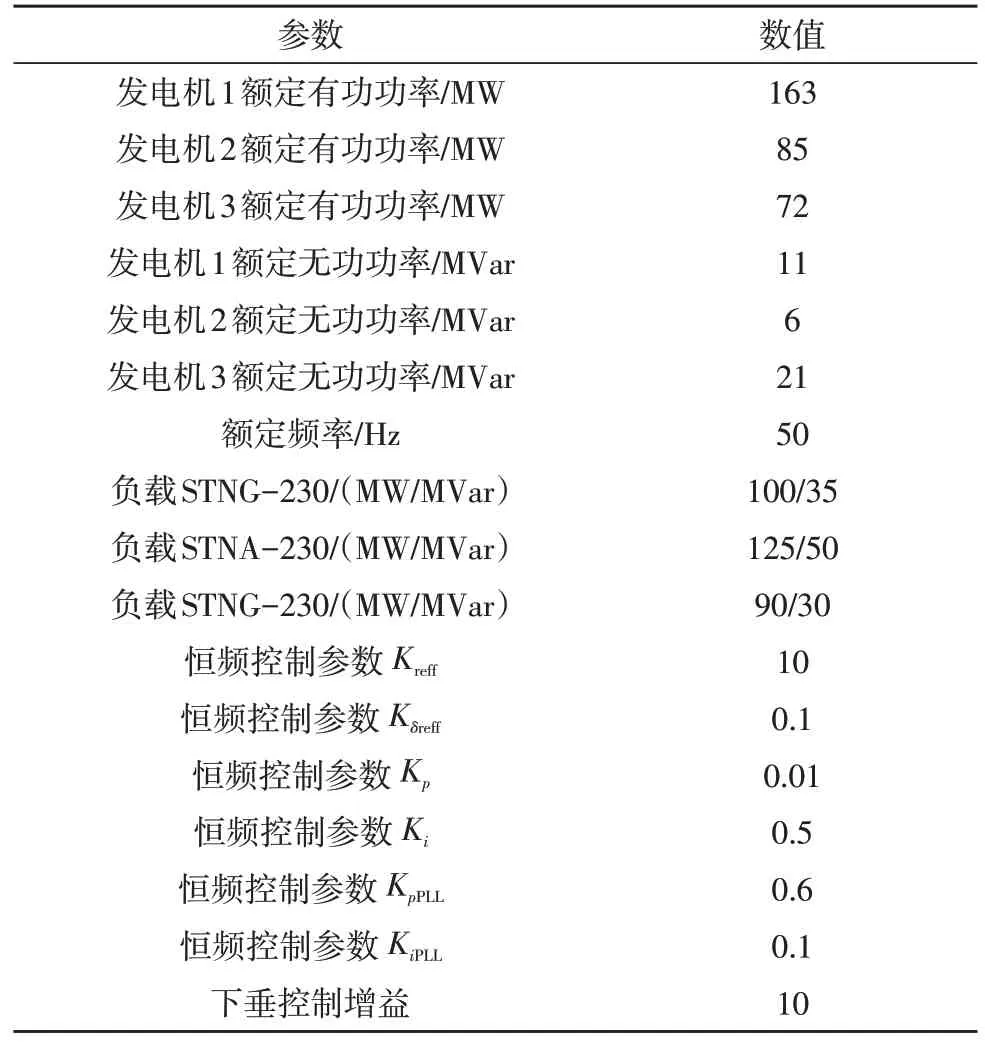
表1 CFCNE及三机九节点系统主要参数

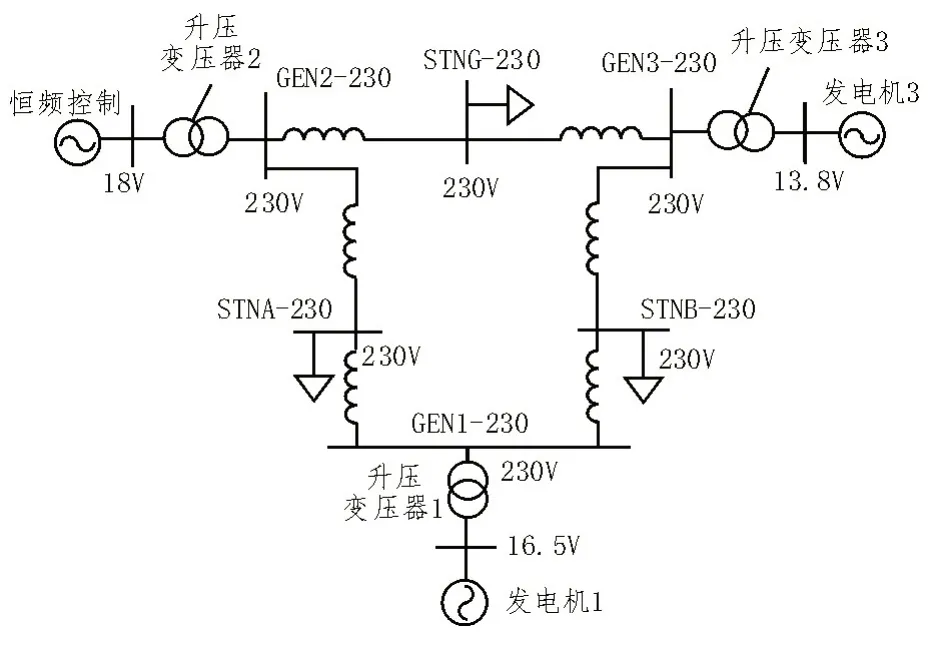
图6 三机九节点结构数据图

3.1 典型故障下恒频控制与下垂控制、惯量控制、下垂+惯量组合控制的特性对比

1）负荷突增扰动

当STNG-230 处负载阶跃增加60 MW 的有功时（占总负荷24%），考虑恒频控制、下垂控制、惯量控制以及下垂+惯量组合控制相同的增益系数，三者的有功输出如图7（a）所示，系统频率变化如图7（b）所示。从图7（b）中可以算出发生60 MW 的功率缺额后恒频控制稳定频率偏差近似为0。频率下垂控制与下垂+惯量组合控制的稳态频率偏差相同，频率偏差约为0.62 Hz，为额定频率的1.24%。惯量控制稳定频率偏差为0.72 Hz，为额定频率的1.44%。可见恒频控制可以较好地维持系统的稳态频率保持恒定，只要采用恒频控制的新能源机组具有足够的能量备用，在系统频率恢复到正常值之前，可以为系统提供更多的有功功率输出，该算例中的暂态过程中采用恒频控制时最大的频率偏差仅为0.4%。而下垂控制和惯量控制以及下垂+惯量组合控制方式分别达到了2.4%、3.2%、2.4%。可见从系统频率的稳态和暂态两个维度恒频控制都优于其余三种控制。从图7（b）中还可以看出惯量控制响应系统频率变化率，当系统频率上升时会造成惯量控制输出功率的下降，延缓系统频率恢复。下垂+惯量组合控制与下垂控制相比延缓了频率下降的速率，其暂态频率的最低点也有一定改善，稳态频率也与下垂控制基本相同。

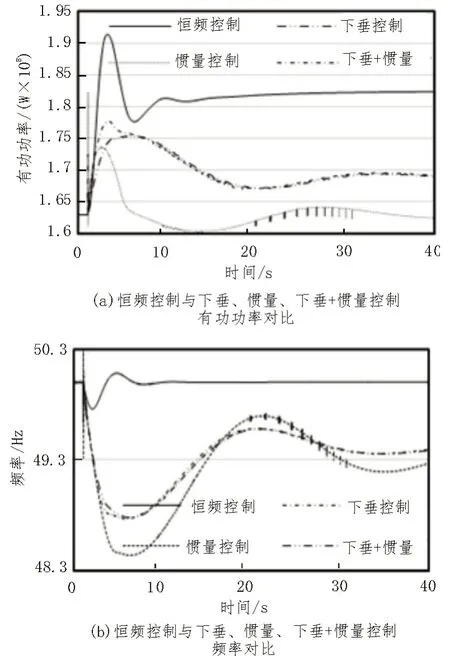
图7 恒频控制与下垂控制惯量控制及下垂+惯量对比

2）短路故障

系统STNA-230 处在1 s时发生持续时间0.1 s的三相短路故障。系统内另外两台同步机的相对功角差如图8 所示，从图中可以看出在传统下垂控制和惯量控制以及下垂+惯量控制时，系统内另外两台同步机相对功角差振荡幅值低于恒频控制，振荡时间也短于恒频控制。故恒频控制虽然可以在负荷波动下较好地维持系统频率恒定在额定频率，但由于本身存在如图9 所示的虚拟功角，在系统发生三相短路等故障扰动时，其虚拟功角也会参与传统发电机的功角相对摇摆，容易造成系统内其他机组的相对功角产生更大幅度的功角振荡，需要引起关注，在后续的研究中进一步开展研究。

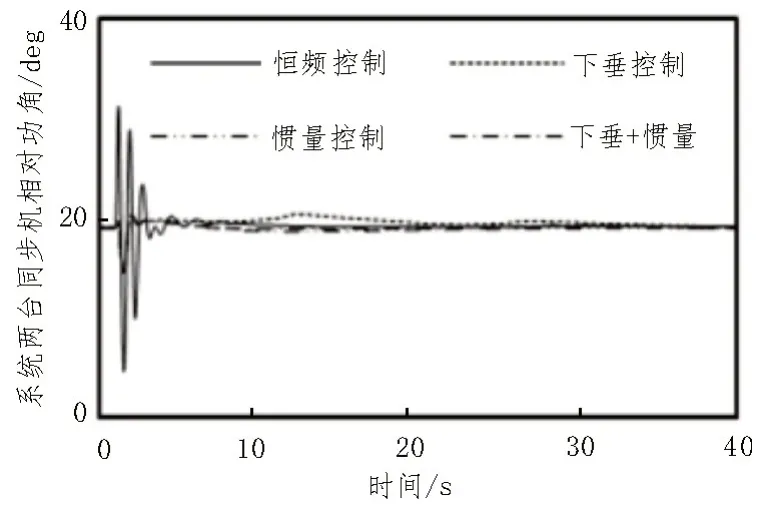
图8 不同控制模式下系统内另外两台机相对功角差

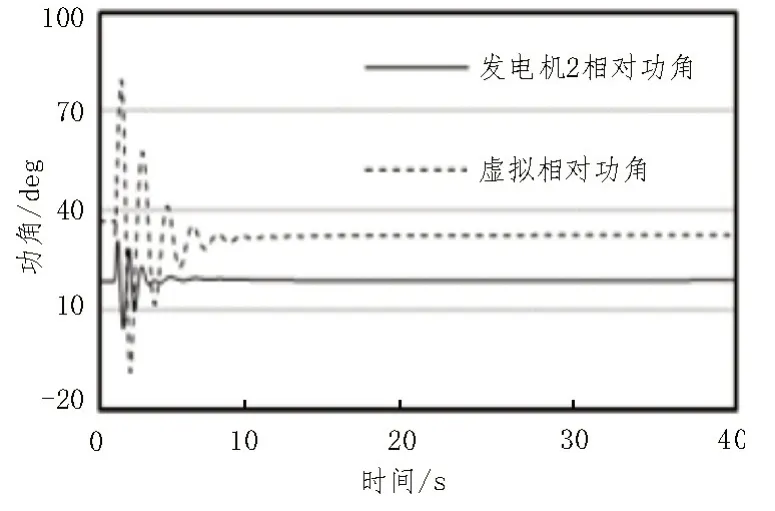
图9 恒频控制虚拟功角与同步机2相对同步机3的功角

3.2 多个CFCNE场站在扰动后的有功功率分担特性

在三机九节点系统中用发电机2、3 代表两处CFCNE 场站，当STNG-230 处负载发生60 MW 的有功缺额时，设置系统中两处场站中的恒频控制参数相同，其功率分配情况如图10（a）所示。从图中可以看出CFCNE 在经过暂态调整后，达到稳态时可以有效地分摊系统出现的有功缺额，两处CFCNE 场站承担的输出有功功率的比值为1∶1.1。改变恒频控制的增益为1∶2，系统中两台恒频控制功率分配情况如图10（b）所示，两台恒频控制输出有功功率的比值为1∶2.25。对比图10（a）和图10（b）可以看出，CFCNE输出的有功功率不仅取决于恒频控制的增益，还与系统的网络拓扑结构相关。

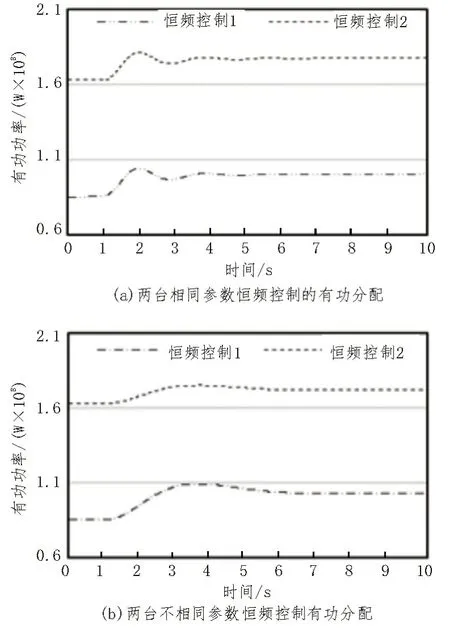
图10 恒频控制的有功分配

4 结论

该文推导了CFCNE 的数学模型，基于PSASP 搭建了恒频控制机电暂态模型，通过与下垂控制、惯量控制以及下垂+惯量控制的仿真对比验证了模型的正确性和优越性并得到如下结论：

1）在调频容量充足的前提下，考虑相同的调节增益，CFCNE 相比下垂控制、惯量控制以及下垂+惯量控制的新能源，对系统暂态频率支撑能力更强，系统暂态频率极值和稳态频率值均优于后三者。

2）由于CFCNE 内部存在虚拟功角，在多机系统中会参与功角摇摆过程，一定条件下可能产生更大振幅和更长时间的振荡，影响系统整体的功角稳定特性，恒频控制大规模应用时需要重点关注。

3）当系统中存在多个CFCNE 场站时，系统的不平衡功率可以在其间自主有效分配，功率分配特性与恒频控制的增益以及系统拓扑结构等因素相关。