基于小波变换与LDPC 码的图像加密

邵一丹，王中训

（烟台大学物理与电子信息学院，山东烟台 264005）

网络日益发达，有着许多信息载体。数字图像也因保真度比较高、形象生动等特点成了网络交流中最广泛的沟通介质[1]。但在实际的网络生活以及现实生活中，存在着大量图像被冒用的问题，版权受到侵害，就比如有部分人会盗用别人的照片进行违法活动，侵犯了他人的隐私。没有人希望自己的隐私被侵犯，因此，图像的信息安全成为人们关注的焦点，迫切需要一些图像加密技术对图像信息进行保护[2]。

图像信息冗余大，一般对文本加密实用的DES、3DES 等加密算法在图像上并不能取得较好的效果[3]，出现了混沌加密。由于较早出现的很多混沌系统很容易被攻击并且被破解而造成信息暴露，又出现了高维混沌系统、超混沌系统以及其他手段如深度学习、小波变换等与混沌系统相组合的图像加密操作。

为了提高图像的安全性，采用了小波变换与混沌系统相结合的方案，首先对图像进行加密，然后通过LDPC 码进行了水印调制，将水印信息嵌入图像，有着较强的抗攻击能力，破解出原图不是很容易。

1 LDPC概述

LDPC 码是由Gallager 提出的。它也可以称为低密度奇偶校验码，究其原因，是每行每列存在的非“0”的数目很少，也是基于这一独特的稀疏性才能构造出它低复杂度、高性能的特点[4]。在码长足够长时，LDPC 码经过适当的编译码后，可在加性高斯白噪声信道中达到接近香农容量的性能[5]。

HM×N为校验矩阵，码字信息在其中是用“列”来对应的，把每一列出现的不为“0”的个数记为列重，用λ来表示；“行”对应的则是校验信息。每一行出现的不为“0”的个数记为行重，用ρ来表示。列重与行重相对于M、N来说，都是很小的。LDPC 码可用(n,ρ,λ)表示，满足HcT=0 的条件。以（8，4，3）来举例。

校验矩阵如下：

校验方程组如下：

采用BP 译码方式，经典的置信传播（BeliefPropagation,BP）算法是一种软判决算法[6]。初始化变量节点，下一步，变量节点通过与校验节点相连的边将概率信息传递给校验节点。通过校验节点之后的信息更新后，经过传递再次到达变量节点中，变量节点依据更新以后的信息作判决，这是一次迭代的过程。最终结束译码的条件是找到了允许使用的码字，或者是到达了最大迭代次数。通过多次迭代计算使得译码结果更加精准，误码率更低[7]。

2 混沌系统与小波变换

2.1 混沌系统

通常混沌可以看成是一类在确定性系统中生成的不规则的、复杂的现象[8]。混沌有着独有的特征，如：

1）敏感的初值；

2）有界性，整体来说较稳定；

3）遍历性。

混沌的发现是一个突破，许多领域都有着对它的运用，在加密方向更有独特魅力。在混沌图像加密算法设计中，一个值得重视的焦点为安全性，算法效率也是值得关注的问题[9]。

常用的混沌系统Logistic 映射公式为：

文中采用的是Chun Cao 等人提出的二维超混沌映射，所用的公式如下：

其中，参数a以及参数k的范围都是（0，+∞）。

Logistic 分岔图如图1(a)所示，超混沌系统的状态图如图1(b)所示。

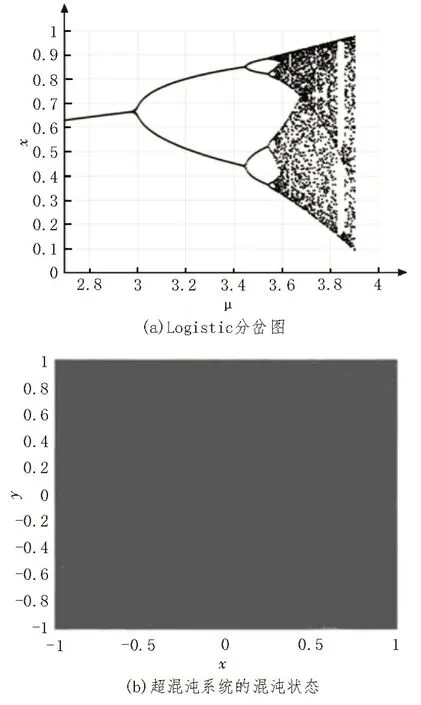
图1 混沌比较

从图中可以看出，超混沌系统是全混沌状态，混沌范围宽，复杂度大。

2.2 小波变换

小波变换的概念大约在19 世纪80 年代由J.Morlet 提出，并逐步发展完善。小波变换突破了傅里叶变换的局限性，将数学应用到图像处理的很多领域中[10]，它能精确处理细节部分，成为处理图像的热点以及重点方式之一。

小波变换是把图像的像素矩阵变换到频域，然后对频域的数据进行处理[11]，这样就实现了对图像的处理。作为信号时域分析方式中的一种，小波变换在描述信号局部特征、同步得到时间、频率信息中有着有利作用。经过对系数的加密，局部的变化会通过小波逆变换对图像的所有像素产生影响[12]，因而很大程度上提高了效率。

整数小波变换可实现无损压缩，能够实现变换系统的能量在频率上、空间上的同时集中，达到去除像素冗余的效果。整数小波变换有着简单的结构，运算量也不是很高，占用的存储空间不多。

d1,n为高频系数，s1,n为低频系数。这里是一级分级，将分解结果再次代入式（5）中，得到高级分解系数。对图像的行和列进行小波分解操作，得到的系数矩阵可采用式（6）系数进行逆变换，最终组合成原始图像。

式中，j为分解级数。经过小波变换后，有四个分量:内容缩略图ll，数据能量集中于此；水平方向的高频信息hl，反映变化、边缘信息；垂直方向的高频信息lh，以及对角线方向的高频信息hh。

3 图像处理过程

3.1 图像加密

选取的图像大小为256×256，记为原始图像，如图2 所示。

图2 原始图像

读取图像后，首先进行小波变换。进行分解，获得每级小波分解后的四个频率子带。第一级为(ll1,hl1,lh1,hh1)，分解图像如图3(a)及图3(b)所示。同理可得小波2 次分解如图3(c)及图3(d)所示，小波3 次分解如图3(e)及图3(f)所示。

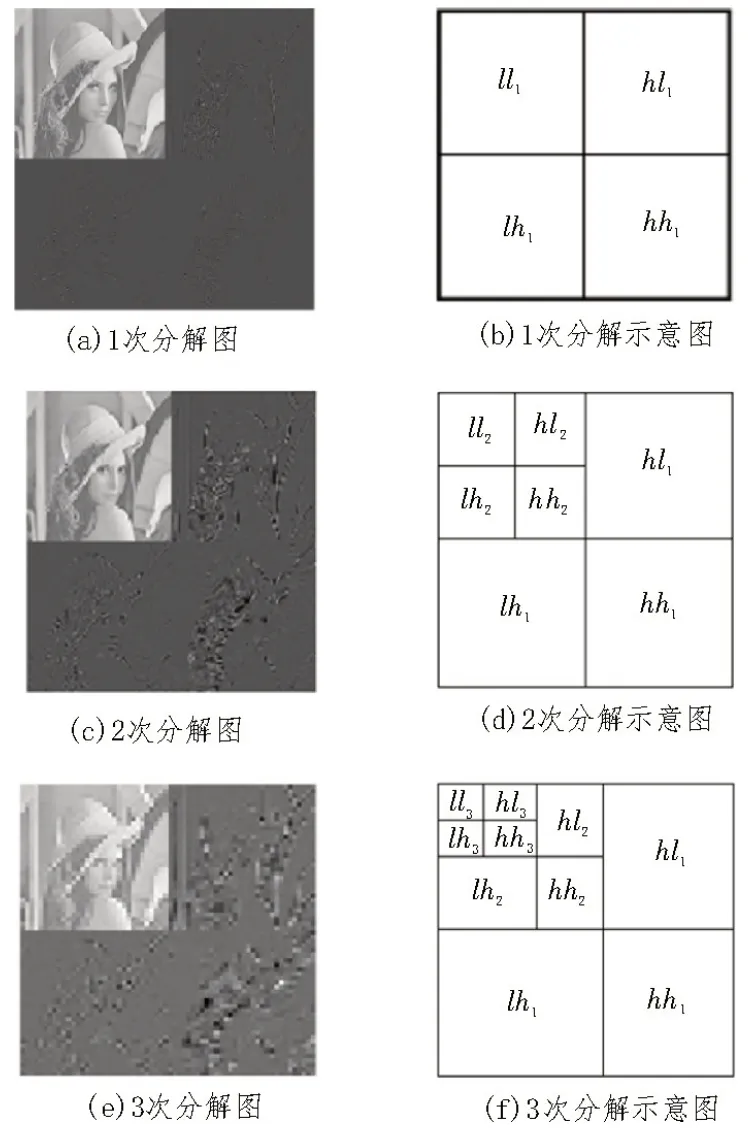
图3 分解图级示意图

产生混沌的参数设置如下：a=0.600；k=0.800；x0=0.123 419 94；y0=0.567 819 88；

对ll3进行扩散与置乱，再对hl2、lh2分量进行扩散与置乱。最后将系数进行组合以便显示图像。

加密后的图像如图4 所示。

图4 加密后图像

3.2 LDPC嵌入水印

数字水印技术可保护版权。把信息嵌入图像中，这些信息可以是数字、图片等，嵌入后人类肉眼是不能感觉到的，对载体图像不产生影响，还能维护自己的权利，也是一种保护图像的方案。图5 为LDPC 码与水印系统信道模型图。

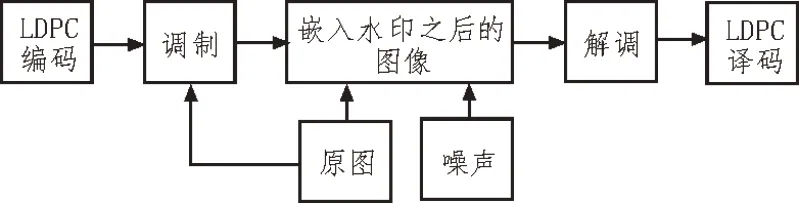
图5 LDPC码与水印系统信道模型图

LDPC 嵌入水印所用到的公式为：

式中，X为DCT 系数，a为嵌入强度。

水印图像如图6(a)所示。将经过LDPC 调制后的水印嵌入，结果如图6(b)所示。

图6 水印图及嵌入水印图

提取水印图像如图7(a)所示。解密图如图7(b)所示。

图7 提取水印图以及解密图

4 结果分析

4.1 信息熵分析

信息熵H(S)定义如下：

S记为信源，si为S包含的消息符号，状态数目为q，P为出现的概率。信息熵最大值出现的情况是出现信源符号的等概率分布。假设图像灰度级是256，那么，信息熵H(S)能够达到的最大值是8 bit。信息熵值越大，可见不确定性越大，也就是可视的信息较少，安全性越高[13]。加密后信息熵约为7.8 bit，比较接近于8 bit。

4.2 密钥空间分析

加密密钥的范围即密钥空间，这个空间越大越好。穷举攻击，即对所有可能范围内的密钥都进行尝试，直至找到正确的密钥[14]。不是很容易被暴力破解加密方案往往有着比较大的密钥空间。四个参数为52 bit，密钥空间至少为24×52=2208。

4.3 密钥敏感性分析

密钥敏感性是密码学中最基本的要求[15]。用错误的参数进行解密，选择a=0.600 000 01；k=0.799 999 99；N=10 000；x0=0.123 419 94；y0=0.567 819 88；改动参数解密后图像如图8 所示。由此可以看出虽然改动细小，但仍然无法成功解密出原图。密钥是较为敏感的，足以保证消除抵抗穷举攻击的危险[16]。

图8 错误解密图

4.4 抗攻击能力

进行剪切攻击仍可提取出完整水印，经过剪切处理后提取的水印图像如图9 所示。

图9 经过剪切处理后提取的水印图像

5 结论

文中实现了LDPC 码与小波变换以及超混沌系统相结合，相对于单一的混沌系统有着更大的密钥空间，更能抵御攻击，提高安全性。加密效果也较好，无法用肉眼观察到信息。嵌入的水印也可以抵御攻击，有利于维护版权。但在信息熵看来，不是特别完美，还需要有一定改进。另外，LDPC 码的编译码也可以进行改进，以提高速率。LDPC 码也可以和高维混沌系统相结合，以增强图像的安全性。