双质量飞轮关键传动零件受力与疲劳寿命分析

曾礼平，徐宇鲲，吴浪武

（1.华东交通大学机电与车辆工程学院，江西 南昌 330013；2.南昌市车辆智能装备与控制重点实验室，江西 南昌 330013；3.南昌大学科学技术学院，江西 南昌 330029）

1 引言

目前，双质量飞轮在汽车中的应用越来越广泛，其具有比传统扭振减振器更好的减震性能[1−2]，很多汽车制造商如通用、宝马、本田等的多种车型都采用了双质量飞轮。研究人员为开发出更优性能的产品不断进行深入研究，如文献[3–4]分析了刚度具有分段变化特征的双质量飞轮非线性振动特性；文献[5]针对某微型客车存在的扭转振动引起的噪声问题，利用遗传算法对传动系扭转振动问题进行优化，并用试验验证了理论分析准确性；文献[6]利用离散方法对长弧形弹簧双质量飞轮的动力学特性进行了理论分析和试验研究；文献[7]提出了一种多工作间隙的磁流变液双质量飞轮，通过理论分析和结构优化设计，使其阻尼力最大化。在加工工艺方面，文献8]等建立了双质量飞轮的驱动齿盘旋压成形分析模型，分析了旋压增厚的成形工艺，并通过试验进行验证。

双质量飞轮减振元件在初级飞轮与次级飞轮间传递动力和旋转运动，由于输入转矩的波动，实际工作中的减振元件所承受的载荷也不断变化，这使结构将产生变应力，此时零件的疲劳强度一般比静载荷下的强度极限低很多，甚至比屈服极限低[9]，从而使变应力下零件经常发生疲劳失效。因此，作为减振关键零部件，变载荷作用下结构强度及疲劳寿命必须保证。通过分析减振元件相互作用力，建立双质量飞轮动力学分析模型和有限元分析模型，对弹簧座的强度和疲劳寿命展开分析。

2 双质量飞轮结构和工作原理

周向短弹簧双质量飞轮主要由初级飞轮总成、次级飞轮总成和两飞轮之间的减振元件通过一定的联接方式组合，如图1所示。

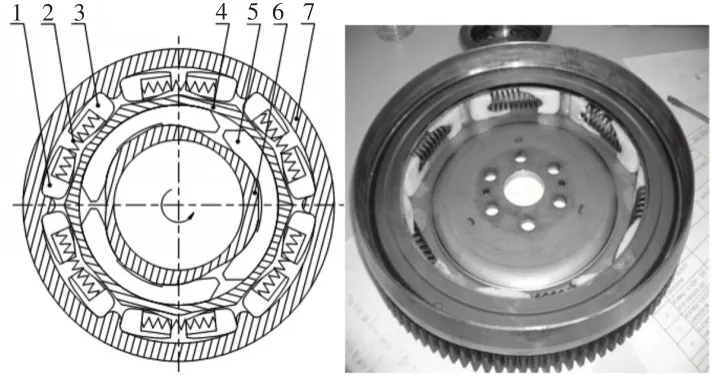
图1 双质量飞轮结构Fig.1 DMF structure

在双质量飞轮中，动力和运动路线是由发动机—初级飞轮7—弹簧座1—弹簧2—弹簧座3—次级飞轮4最后到变速箱的顺序进行传递的。

3 动力学分析模型

为分析工作时双质量飞轮关键传动部件疲劳寿命，将系统传动部分简化，将次级飞轮与弹簧座看成固定不动，建立初级飞轮、减振元件、次级飞轮单自由度动力学微分方程：

式中：θ—相对转角；J1—初级飞轮与弹簧座的综合转动惯量；c—阻尼；Fs—单根弹簧作用力；M—发动机输入的转矩。

发动机扭转激励转矩可用三角级数展开[7]：

式中：M0—平均转矩；Mr—r次简谐转矩的幅值；r—简谐次数；

ψr—r次简谐转矩的初相位；ω—曲柄角速度。

根据文献[10]，不同发动机的输出转矩特性亦不同，由于缸数为偶数的发动机应用最广泛，其偶数谐次对应的输出转矩贡献量明显大于奇数谐次对应的输出转矩，因此只分析主要偶数谐次转矩输出。

图2中R—减振弹簧分布半径，弹簧初始长度为L0=2Rsin（θ0/2），θ0—对应的初始张角。当相对扭转角为θ时，弹簧长度变为：

图2 结构参数Fig.2 Structure Parameters

弹簧压缩变形后作用力Fs大小为：

式中：kt—减振弹簧的线刚度。

如图3所示，弹簧座受到初级飞轮和次级飞轮作用力分别为N1和N2，不考虑弹簧座重力和惯性力作用，弹簧座在Fs、N1、N2三个作用力下平衡，三力汇交于点E，因此：

图3 弹簧座受力分析Fig.3 Force Analysis of Spring Seat

4 弹簧座有限元分析建模

由于发动机输出转矩的波动以及负载、其他外界激励的变化，双质量飞轮在工作过程当中传动零部件受到的载荷为变化状态，因此有必要对零件的结构进行强度分析。通过分析双质量飞轮的动态特性，可得到弹簧座受到的最大载荷，以此作为有限元静强度分析的载荷条件。结构三维模型导入Hyperworks软件，因为结构比较复杂，结构中的小特征比较多，例如小的圆角、倒角和薄壁等，所以划分单元网格的尺寸也比较小，这里按照0.6mm单元长度进行划分，完成弹簧座有限元模型的建立，如图4所示，全部划分成三维单元网格。单元总数为139639个，节点总数为31121个。

图4 弹簧座有限元分析模型Fig.4 Finite Element Analysis Model of Spring Seat

在弹簧座与次级飞轮和初级飞轮接触位置施加全部约束，在弹簧安装位置施加弹簧力，并将弹簧力平均施加到此位置的每个节点处。按照疲劳寿命分析的要求，在有限元分析模型中，首先将单位弹簧力施加到弹簧安装位置处，然后施加载荷时间历程，定义材料S−N 曲线。根据文献[11]，塑料的疲劳特性曲线可采用Basquin公式进行估算：

式中：N—应力循环次数；b—疲劳强度指数；σf—疲劳强度系数；σN—最大应力。

由于试验条件有限，参考文献[12]中对Pa66材料的疲劳测试所获得数据，并以式（7）形式进行拟合处理，拟合后的参数为：σf=18055，b=−0.3974，得到的弹簧座近似疲劳特性S−N曲线，如图5所示。

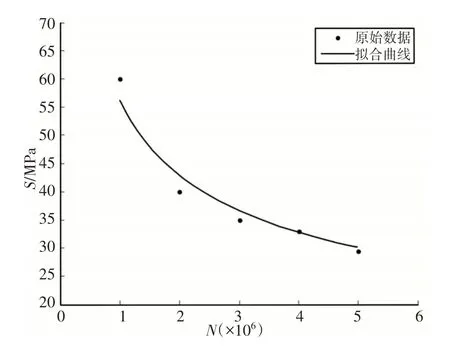
图5 Pa66疲劳特性曲线Fig.5 Fatigue Characteristics Curve of Pa66

基于S−N曲线的机械结构疲劳分析主要关注的是高周疲劳区域，不考虑低周疲劳特性（循环次数小于1000次）[13]，根据图5，在Hyperworks软件中的RADIOSS分析模块设置的弹簧座S−N曲线，如图6所示。

图6 疲劳分析输入的材料S−N曲线Fig.6 Material S−N Curve Inputted into Fatigue Analysis

5 实例分析

双质量飞轮参数如下：初始转角θ0=35°，R=113 mm，减振弹簧线刚度kt=8.19N/mm，结构内部总阻尼c=0.085N·m（/deg/s），φ1=14°，φ2=79°。发动机输出平均转矩M0=160N·m，r=2，M2=200N·m，n=3000r/min，用数值方法求解双质量飞轮动力学方程初始条件是：初始相对转角和相对转速都为0。弹簧座的主要材料特性，如表1所示。

表1 弹簧座主要材料特性Tab.1 Main Material Properties of Spring Seat

采用数值求解方法求解式（1）～式（6），分析得到双质量飞轮动态特性，如图7所示。相对转角和减振弹簧作用力变化趋势基本一致，在起始阶段变化幅度较大，由于双质量飞轮减振作用，振动得到衰减，相对转角和减振弹簧作用力趋于稳定，最大相对转角为21.9°，减振弹簧最大作用力为345.8N。0.2s之后相对转角和弹簧作用力分别在15°和236N左右小幅度波动。

图7 相对转角与弹簧作用力时间历程Fig.7 Time History of Torsional Angle and Spring Force

在弹簧座上弹簧作用力方向施加最大载荷345.8N，与初级飞轮和次级飞轮的接触面上约束全部自由度，进行弹簧座的静强度分析，分析结果，如图8所示。

图8 弹簧座等效应力分布Fig.8 Von Miss Stress Distribution of Spring Seat

结构上最大等效应力位于弹簧座与弹簧接触面的外侧，为6.553MPa，最大变形位于弹簧座导向末端，为0.002mm，Pa66 材料的屈服强度一般在50MPa以上，尤其是一些改性增强后其屈服强度都在100MPa以上，所以静态加载作用下结构的应力和变形量都比较小，满足零件安全工作要求。得到的变载荷作用下弹簧座疲劳寿命云图，如图9所示。

图9 弹簧座疲劳寿命云图Fig.9 Fatigue Life Cloud Picture of Spring Seat

结果显示弹簧座的大部分区域循环次数均大于1019，循环次数最小的区域位于弹簧座与弹簧接触面的外侧，与静强度分析得到的最大应力位置相同，最小循环次数为1.497×108。求解二阶偏微分方程（1）时，模拟的是发动机转速为3000r/min情况下的发动机输入转矩，假设此转速下的车辆行进速度为60km/h，计算后车辆可行驶路程约为1.25×106km，即125万公里，可见使用寿命是非常长的。

综上所述，弹簧座的静强度较高，并且在循环变载荷作用下的弹簧座具有较长的疲劳寿命，在此分析基础上，今后可对弹簧座结构作进一步进行优化设计，在保证结构安全可靠和较长使用寿命的基础上使弹簧座和双质量飞轮的结构更紧凑、尺寸减小，节省材料。

6 结论

通过对减振元件的受力分析，建立了双质量飞轮动力学分析模型，通过数值求解得到双质量飞轮工作过程中随时间变化的相对转角和减振元件载荷。

建立了弹簧座有限元分析静强度和疲劳寿命分析模型，分析了弹簧座的静强度和变载荷作用下的疲劳寿命。分析结果表明弹簧座满足强度和疲劳寿命要求，为弹簧座进一步优化设计、提高结构紧凑性和节约材料提供参考依据。