动态场景下AGV视觉目标跟踪研究

罗川，周军，4，5，张玉雪，皇攀凌

（1.山东大学机械工程学院，山东 济南 250061；2.山东大学高效洁净机械制造教育部重点实验室，山东 济南 250061；3.山东大学机械工程国家级实验教学示范中心，山东 济南 250061；4.山东省工业技术研究院，山东 济南 250061；5.山东亚历山大智能科技有限公司，山东 济南 250061）

1 引言

视觉跟踪技术是一种借助于视觉传感器[1]，对目标特征进行分析，从而实现对其跟踪的技术，目前在军事制导、无人侦察、智能监控和工业机器人等方面应用十分广泛[2]。面向智慧工厂的AGV（Automated Guided Vehicle），为了提高其灵活性，及其与人交互的能力，视觉目标跟踪技术起着至关重要的作用。在工厂内，AGV跟踪场景的复杂多变是一个影响跟踪效率的关键因素，因此在动态场景中如何准确地提取目标特征，合理地训练分类器，保持高效的跟踪已成为一个具有重要意义的研究问题[3−4]。

随着应用研究的不断深入，在计算机视觉领域，涌现出了大量优异的目标跟踪算法。文献[5−6]运用深度学习的算法在公开挑战赛中取得比较优秀的跟踪精度，但限于其对于大数据量的要求，训练模型比较复杂，在一定程度上影响了跟踪的实时性。基于相关滤波的跟踪方法因其算法简单、处理速度快，在实际应用中得到了越来越多的重视，基本的跟踪框架[7]，如图1所示。

图1 基于相关滤波的跟踪基本框架Fig.1 Tracking Framework Based on Correlation Filtering

文献[8]提出一种最小均方差输出和（Minimum Output Sum of Squared Error，MOSSE）滤波器算法，首次将相关滤波的方法引进跟踪领域，该算法利用模板滤波器与目标窗口进行卷积，求解最大响应位置，相比于传统权重分类器的方法，在当时大幅提高了跟踪性能。

文献[9]借鉴MOSSE 算法经验，使用灰度特征对目标进行描述，提出一种结合核函数的循环检测与跟踪（Circulant Structure of Tracking−by−detection with Kernels，CSK）模式，通过循环采样代替滑动窗口采样，有效地增加关联训练样本的同时，进一步提高了运算效率。借鉴上述研究工作，许多研究学者在相关滤波基础之上不断改进完善跟踪结构，在保证跟踪效率的同时提高跟踪准确率，比较典型的算法是KCF算法和SA算法。

以AGV为载体，根据其速度较慢和动态变化的运动特点，选取OTB−2013数据集中具有动态背景的数据模拟AGV实际运行情况，研究其在相关滤波算法下的跟踪情况。

首先介绍上述两种跟踪算法的基本原理，并对两种算法加以改进融合，提出一种新的Sa−KCF 算法，从跟踪效率和跟踪准确率两个方面，通过实验结果对比，评估这些方法在动态场景中AGV跟踪效果的优劣。

2 基本算法原理

2.1 KCF算法

KCF算法以CSK算法为基础，用多通道HOG图代替单一通道灰度图来表达特征属性[10]，提取图像特征来初始化分类器，用高斯核函数判断目标样本与待测样本之间的相关性。该算法将运算过程从时域转化成频域运算，大大降低了运算量，提高了运算速度，使算法满足实时性要求。

首先对视频输入后的第一帧图像的目标周围位置进行密集采样，生成足够多的正负样本训练集，密集采样借助循环矩阵结构在目标中心位置移动，假设样本图像为1 ×n维的向量x，根据循环矩阵在傅里叶空间可对角化的性质，循环矩阵X结构如下：

式中：F—DFT常量矩阵；

∧—向量的傅里叶变换；

H—矩阵的共轭。

对正负样本集提取特征，将其送入分类器进行训练，保证岭回归最优解ω的同时使得损失函数最小[11]，岭回归数学模型如下：

式中：f(xi)=ωTxi—原始样本图像的线性组合；

λ—正则化参数。由式（2）可求得：

将低维线性不可分的数据通过核函数映射到高维空间，使其非线性可分，由此可得：

式中：K—样本间的核相关矩阵；

a—样本数据由低维转化成高维时的系数。

由此倒推可计算出ω。据训练获得的分类器对新一帧图像z进行核相关性分析，即相关响应值计算如下：

式中：φ(x)—从低维空间到高维空间的映射函数。

由响应值最大的位置确定新的目标位置，并以此更新分类器，如此循环，实现对目标的跟踪。

2.2 SA算法

SA算法是在KCF算法基础之上添加了尺度更新的模块［12］，使得跟踪尺寸能够根据目标的运动自适应地进行变化，提高了跟踪的精度。首先定义跟踪框模板尺寸sT=(sx，sy)，尺度变化池为S={t1，t2，…，tk}，假设原始图像目标框尺寸为st，在当前帧中从{tist|ti∈S}中取样k个尺寸，每次进行尺度更新时，使用双线性插值方法将取样初始尺寸固定到sT大小，然后通过式（6）计算相关性最大响应值：

通过调整t的大小得到目标运动的真实偏差。由于跟踪框模板尺寸是固定不变的，因此更新过程只需对双空间系数α和基础数据模板进行更新即可，更新过程为：

SA算法从多个尺寸的滤波器中自动学习背景信息，求出目标中心位置和最大响应值，以此作为当前帧图像的跟踪结果。

3 改进算法

由于传统的KCF 算法在目标跟踪过程中，跟踪框的尺寸是由第一帧确定的，后续跟踪过程中固定不变。当AGV发生转动或目标之间的距离发生变化时，被跟踪物体在尺度方面就会发生变化，原始跟踪框与真实被跟踪物体之间产生尺度误差，导致下一步对于目标特征的提取不准确，如此反复产生累计误差，严重影响后续过程的跟踪精度。

针对这种问题，以KCF为基础框架，融合SA算法中的尺度更新策略，提出一种尺度自适应的Sa−KCF算法，既继承了KCF算法中循环取样和高斯核计算的快速性，又吸收了SA算法对于尺度更新带来的准确性，如图2所示。

图2 Sa−KCF算法流程图Fig.2 Sa−KCF Algorithm Flowchart

由于SA算法的尺度变化池含有多种尺度，这在满足跟踪精度的同时也降低了跟踪效率，为了兼容KCF算法的高跟踪效率和SA算法的高跟踪精度，改进SA算法的尺度大小和尺度数量，选取尺度变化池为S={1，1.05，0.95}，尺度更新准则如下：

式中：maxft(z)—第t帧跟踪目标框的峰值响应；

maxft+1(z)—当前第t+1帧对于选取尺度的跟踪目标框的峰值响应。

对在选取尺度下的峰值响应做减益，减益参数为0.95，若响应值仍大于上一帧的峰值响应，则选取该尺度为当前帧跟踪框的跟踪尺度，否则尺度不变。

传统KCF 算法对于彩色图像的跟踪是将其转化为灰度图，然后再提取HOG特征，单通道处理提高了运行效率，但这一做法在某种程度上损失了跟踪目标的特征信息[13]。算法针对AGV运行过程速度较慢这种情况，维持原有RGB图像3通道处理，平衡跟踪精度和跟踪效率之间影响。

4 实验结果与分析

4.1 实验设备与参数

所使用的实验平台为笔记本PC机，操作系统为Windows 10 64bit，CPU为Inter Core i7−8700，GPU为NVDIA GeForce 1050Ti，主频为3.20GHz，内存为8GB，测试平台为Matlab 2019b。所选用的实验标准为OTB−2013基准[14]，采用跟踪时间和跟踪准确性作为算法的评价指标。所对比的算法使用的参数均为文献[10−13]中提供的默认数据。

跟踪时间是指跟踪算法运行完一段视频序列所使用的时间，时间越短说明跟踪效率越高。跟踪准确性从跟踪的精度和成功率两个方面进行分析。跟踪精度是指跟踪算法估计的目标中心位置与人工标注的目标中心位置之间的偏差，该值越小说明跟踪精度越高。成功率是指跟踪算法估计的目标框与人工标注的目标框的重叠值，该值越大说明跟踪成功率越高，计算公式如下所示：

式中：OS—重叠率；BT—目标跟踪框；BG—人工标注框。

根据应用研究要求，选择测试数据集OTB−2013 中具有动态背景的10组图像序列，对比KCF、SA和改进Sa−KCF算法的跟踪效果，如表1所示。

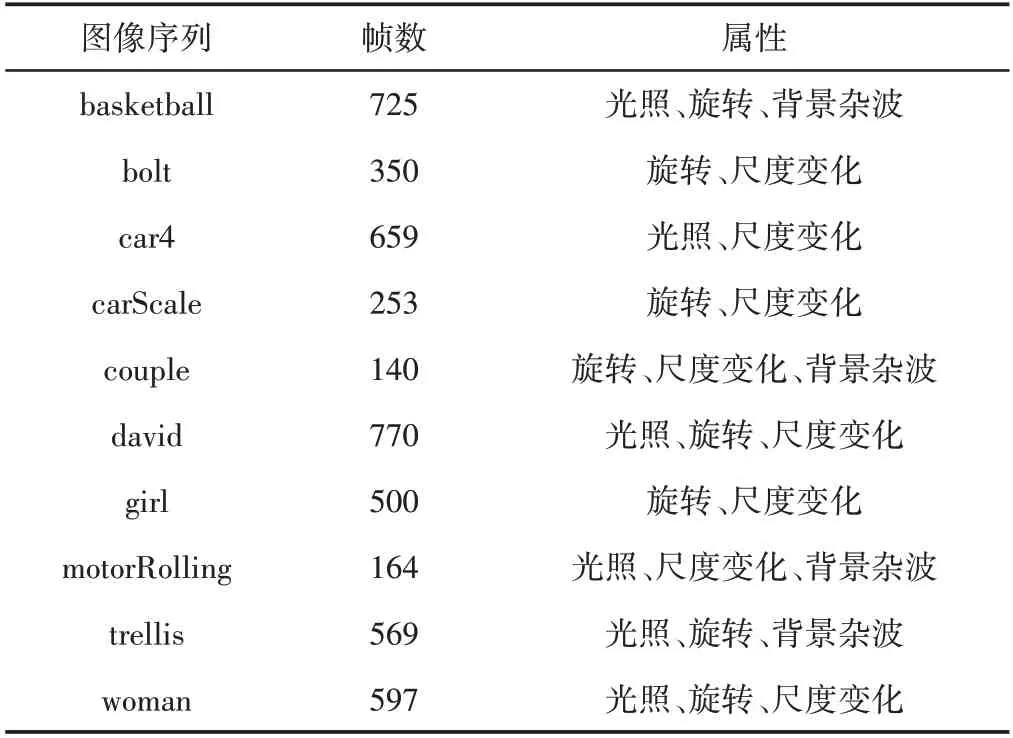
表1 OTB-2013中10组实验图像序列Tab.1 Ten Experimental Image Sequences in OTB-2013

4.2 结果分析

4.2.1 定量分析

首先对三种算法测试表1中10组图像序列，分析其实验结果，获得的跟踪精度和成功率用OPE、SRE和TRE来表示，如图3、图4所示。由图可知，通过对10组图像序列进行实验比较，三种算法中，Sa−KCF 算法在跟踪精度和成功率方面表现效果最好，KCF和SA算法表现次之。

图3 跟踪精度图Fig.3 Tracking Precision

图4 跟踪成功率图Fig.4 Tracking Success

在保证跟踪准确性的同时，跟踪效率的高低对实时性起着至关重要的作用。实验中三种算法的跟踪效率用每分钟处理的帧数（FPS）来表示结果，如表2所示。

表2 跟踪效率FPS对比Tab.2 FPS Comparison of Tracking Efficiency

由表1和表2分析可知，Sa−KCF算法在实时性上表现效果，较SA 算法提高了近3倍，尽管较KCF 算法表现稍差，但已满足AGV的实时性跟踪需求。

4.2.2 定性分析

选取两组图像序列car4和basketball中三种算法的跟踪效果对比图，如图5、图6所示。

图5 Car4图像序列部分跟踪图Fig.5 Car4 Partial Tracking Map of Image Sequence

图6 Basketball图像序列部分跟踪图Fig.6 Basketball Partial Tracking Map of Image Sequence

序列car4中，目标在运动过程中发生了尺度变化，周围环境存在光照变化等问题。在第100帧时，三种算法都表现出很好的跟踪结果，但是随着目标尺度发生变化，色差变化较弱，干扰背景信息逐渐累积，在第365帧和650帧中，Sa−KCF和SA算法仍然保持着很好的跟踪效果，KCF算法出现跟踪滞后现象，无法保证尺度上的自适应。序列basketball中，运动员在运动过程中发生姿态旋转，也存在部分遮挡问题。在第21帧时，运动员下半身被部分遮挡，且被遮挡部分颜色特征与遮挡物相近，环境产生干扰。对比第83帧和第124帧，运动员的姿态发生突然变化，SA算法因其运行效率低，跟踪开始出现漂移，随后对于目标跟踪完全丢失，KCF算法和Sa−KCF算法依然保持着良好跟踪[15]。

5 结论

对两种基于相关滤波的目标跟踪算法进行了原理介绍，并对这两种算法加以改进融合，得到一种尺度自适应的Sa−KCF算法。在OTB−2013数据集上选取10组具有动态背景的序列进行试验，对三种跟踪算法在跟踪精度和成功率方面进行定量对比和定性对比分析。实验表明，改进Sa−KCF算法在跟踪准确性上表现比较优异，能较好地针对目标发生尺寸变化进行跟踪调整，在跟踪效率方面，满足AGV目标跟踪的实时性要求。目前相关滤波算法仍然是目标跟踪领域中较为主流的算法，随着深度学习的发展，将深度学习与相关滤波结合起来这一方法取得了良好效果，但耗时增多，因此如何提高跟踪运算效率是接下来的研究难点[15]。