空间含镀层薄膜天线应力均匀化分析与验证

操安博，刘志全，林秋红，邱 慧，李 潇

(北京空间飞行器总体设计部，北京 100094)

0 引 言

近年来，随着航天器大型天线的发展，薄膜结构质量轻、展收比大的优点越来越受到航天器大型天线研究者的关注[1-2]，长度超过10 m、面积超过20 m2的空间大尺度薄膜天线应运而生[3-4]。伴随着薄膜单元拼接技术和薄膜镀层技术的进步，空间大尺度薄膜天线的面积将会进一步增大。这类天线有望成为未来航天器大型天线的主流产品之一。为保证薄膜结构的刚度，一般通过张拉系统对薄膜施加拉力，而薄膜材料固有的黏弹性会使薄膜在拉力作用下产生蠕变[5-6]。蠕变将会改变薄膜结构的形状精度和应力分布，使薄膜表面的元器件偏离设计位置，从而导致航天器难以实现预定功能。蠕变的严重程度与薄膜内应力大小正相关[7-8]，减小应力集中、降低薄膜内应力不均匀性是抑制蠕变的主要措施。薄膜天线需要将辐射单元、馈电网络等元器件以镀层(镀铜和镀铝等)的形式附着在柔性膜面上。这些镀层使薄膜结构内出现非均匀、非连续特征，必然会改变薄膜内应力分布，导致应力集中[9-11]。因此，开展空间大尺度含镀层薄膜天线应力均匀化分析与验证对于有效抑制薄膜的蠕变、延长航天器薄膜结构寿命具有重要意义。

空间大尺度薄膜天线在设计时，一般会以薄膜在拉力作用下应力均匀性最优为目标进行优化，求解薄膜的几何形状，这一优化过程称为找形分析[12]。对找形算法的研究始于20世纪60～70年代，主要针对几何构型简单、材料均质的薄膜进行优化，在建模中忽略了张拉系统、支撑柱等薄膜结构组件，不能真实地反映薄膜结构的特征[13-14]。进入21世纪以来，努力提升模型与实际薄膜结构的接近程度成为业内的研究重点。2008年，浙江大学汪有伟等[15]用非线性有限元法对边索张拉薄膜结构进行了找形分析，并在建模中引入了支撑柱，研究了边界跨数、支撑柱受力与薄膜应力分布的关系。支撑柱的引入使模型更加接近实际，但文献[15]的研究方法仅适用于形状比较简单的薄膜构型。2010年，上海交通大学肖薇薇等[16]用非线性有限元法对三角形薄膜结构进行了找形分析，得到了找形后的应力分布，研究了边索曲线形状对薄膜结构中膜面频率和应力分布均匀性的影响。文献[16]的方法能较好地适应不同构型的薄膜结构，但是在应力分布均匀性的研究中将薄膜和索网分别考虑，未给出两者间的互相影响。2015年，中国空间技术研究院西安分院王朋朋等[17]对索网进行了研究，将应力均匀性与蠕变联系起来。结果表明，蠕变会使索网内部张力重新分配，进而导致天线的形状精度下降。文献[17]建议，选用蠕变速率小的材料来保证张力索网的性能。但是，文献[17]未涉及薄膜自身的蠕变，对除材料外的其他可设计参数也未进行分析。2018年，同济大学丁潇等[18]用非线性有限元法对方形薄膜结构进行找形分析，研究了边索拉力和张紧结构构型对支撑柱受力及薄膜结构基频的影响，提出用“膜面有效面积率”间接评估薄膜应力均匀性。然而，“膜面有效面积率”与薄膜几何构型关系很大，该方法只能适用于相同构型薄膜应力均匀性的评估。2020年，同济大学项平等[19]用非线性有限元法对矩形索膜结构进行了找形分析，得到应力分布较为均匀的薄膜构型，考虑了索网与薄膜间的摩擦力对“膜面有效面积率”的影响，给出了面向应力均匀性最优的索网设计建议。虽然近年来相关建模越来越接近实际使用的空间大尺度薄膜天线，但是建模中考虑镀层对应力均匀性影响的文献未见公开报道。

为获得含镀层薄膜建模所需的含镀层薄膜整体的力学特性参数——杨氏模量和泊松比，需开展试验测得镀层和薄膜两个组分的杨氏模量和泊松比，将试验结果分别代入经典层合板理论公式[20-21]，计算得到含镀层薄膜整体的杨氏模量和泊松比。2004年，美国弗吉尼亚大学Chasiotis[22]研制了一种测量薄膜杨氏模量和泊松比的单轴拉伸试验装置。用该装置进行薄膜试样拉伸时，薄膜在平面内垂直拉力的方向上易产生褶皱，一旦出现褶皱，薄膜横向位移测量结果将会大于实际结果，进而使泊松比的测量出现较大误差。2005年，美国哈佛大学Xiang等[23]用三点弯曲法测量了铜薄膜的杨氏模量和泊松比。该方法测量过程复杂，需对薄膜试样进行蚀刻处理，试样长度一般在毫米级，比空间大尺度薄膜天线的基本单元小2个数量级。因此，若将该试验获得的试验结果推广应用于大尺度薄膜天线的基本单元中，存在放大测量误差的风险。2006年，同济大学陈鲁等[24]研制了一种双轴拉伸试验装置，该试验装置能降低薄膜出现褶皱的风险，测量方法比三点弯曲法更简单。但文献[24]用并列的两个宽度约16 cm的压块来夹持薄膜，压块与薄膜接触处安装橡胶垫，当拉力较大时这种夹持方式难以保证均匀施力，难以保证薄膜的平面度要求，不利于泊松比的测量。该试验装置需通过引伸计测量位移，引伸计与薄膜的接触会影响测量精度。2014年，上海交通大学陈宇峰等[25]研究的薄膜双轴拉伸试验装置用长压板来夹持薄膜，能提高受拉薄膜的平面度。薄膜边长及长压板长度为50 cm。该装置的缺点在于，长压板经2个调节螺栓与外边框连接，试验者需手动调节2个螺栓的旋进深度来调节拉力，这种施力方式很难确保施力均匀。因此，测量薄膜力学特性有必要设计更优的双轴张拉试验装置，解决薄膜尺寸不合适、施力不均匀、薄膜平面度不足等问题。

针对空间大尺度含镀层薄膜天线结构建模中尚未涉及镀层对应力均匀性影响的问题以及双轴张拉试验装置施力不均、薄膜平面度不足的问题，本文进行含镀层薄膜单元力学模型的建模，用经典层合板理论计算含镀层薄膜的力学特性，设计一种均载、平面度保证措施好的薄膜双轴张拉试验装置，用该装置获得理论计算所需的常量。通过有限元仿真分析获得薄膜几何参数、张拉系统拉力、材料参数对薄膜应力均匀性的影响规律。最终通过仿真来校验面向应力均匀性的优化对抑制含镀层薄膜蠕变的效果，为空间大尺度薄膜结构设计提供参考。

1 含镀层薄膜的单元力学模型建立

空间大尺度平面含镀层薄膜天线是由许多个如图1所示的含镀层薄膜单元拼接而成。单元边长为L，单元以薄膜为基底。薄膜基底的杨氏模量、泊松比和厚度分别为Es,νs和ts，下标s(含后文出现的上标s)表示基底(Substrate)。单元中央为含镀层薄膜正方形区域，其边长为l。含镀层薄膜区域内薄膜基底和镀层组合体的杨氏模量、泊松比和厚度分别为Ec,νc和tc，下标c(含后文出现的上标c)表示组合体(Composite)。假设每个薄膜单元边缘受到等大的边荷载Fx=Fy。图1中圆点为采样点，用于后文计算应力均匀性。

图1 平面薄膜天线单元Fig.1 Elements of the space membrane aperture

航天器平面薄膜天线的ts和tc远小于L，符合经典层合板理论[26]的假设。用该理论计算Ec和νc的过程如下。

(1)

式(1)中出现的上标及下标f表示镀层(Film)。含镀层薄膜各部分之间的应力应变关系有

(2)

基于经典层合板理论的假设，各部分应变相同

(3)

将式(2)和式(3)代入式(1)，整理为如下形式

(4)

从而可以得到含镀层薄膜单元(见图1)的力学模型

(5)

(6)

从式(5)中可提取(νs-νf)2项。由于νs和νf差别通常小于0.1，因此该项为小量，可以简化该式。简化后得到

(7)

式(7)表明Ec与Es和Ef呈线性关系。

由式(6)可见，νc表达式能否简化取决于Ests与Eftf的大小关系。根据航天器平面薄膜天线常用的设计参数[27]计算可知，Ests与Eftf处于相同数量级，不能对式(6)进行简化。因此，航天器薄膜天线的力学模型明显区别于文献[26]给出的力学模型。

式(6)、式(7)中，Es,νs和Ef,νf为未知量，需通过下文的含镀层薄膜双轴张拉试验测量获得。

2 含镀层薄膜双轴张拉试验

本文设计的双轴张拉试验装置如图2所示。

图2 薄膜双轴张拉试验装置Fig.2 Biaxial extension test set-up

薄膜试样由4个小车进行夹持和张拉。其中，2个小车固定在支架上，另外2个活动小车通过凯夫拉绳和2个滑轮与砝码相连。活动小车通过下方球窝中的钢球实现在平整光滑的平面上进行无摩擦运动(摩擦力忽略不计)，薄膜受到的拉力大小等于砝码的重力大小。试验过程始终保持薄膜试样在x和y向有足够拉力，避免褶皱出现，确保薄膜的平面度。固定在支架上方的电子散斑干涉仪(Electronic speckle pattern interferometry，ESPI)对准薄膜中心。当薄膜产生变形时，ESPI仪能测得视场内的电子干涉条纹，干涉条纹经处理后可转化为视场内的应变场。相比传统的通过测量夹持点处位移来计算应变的方法，ESPI法能排除夹具形变等因素带来的误差，提高了测量的准确性。小车结构见图2(b)。薄膜试样下方粘贴单面胶带，用于增加夹持部位的摩擦力，防止试样滑脱。薄膜夹持部位采用了台阶状结构，薄膜试样边缘与台阶的棱边平行且重合，使得小车对薄膜施加均匀的拉力。夹持压板与小车车体通过螺栓连接，以此压紧薄膜试样。

金属材料拉伸试验所用试件形状及尺寸有标准规定。而对于薄膜双轴张拉试验，目前国际上尚未形成试样形状及尺寸的标准。为获取最优的试样形状，本文用相关软件通过有限元法对不同试样形状的应力分布进行仿真分析，包括方形倒角试样[25]、正交T形试样[28]、十字形试样[29]，如图3所示。

图3 薄膜试样形状仿真分析Fig.3 Simulation analysis of the membrane sample configurations

文献[29]认为，在十字形试样的非中心区域用激光等工艺制作宽度可忽略、厚度方向贯穿薄膜试样的割缝，能提升试样中心区域的应力均匀性。本文对十字形试样非中心区域上不同割缝数量(0条、3条和7条)情况下的应力均匀性进行了对比，见图3。对试样施加拉力Fx,Fy，计算ESPI采样区的应力大小。在图3的仿真模型中，中心处的方框表示采样区。本文使用的ESPI仪采样区边长为6 mm。在评估不同试样时，选择方框顶边(图3中用实线标出)的受力情况进行对比。根据文献[26]的测量结果，仿真中取试样的Ec=3 GPa，νc=0.3。

根据下式计算预期应力大小

(8)

仿真计算得到的应力与由式(8)计算得到的预期应力之比定义为相对应力，相对应力为无量纲参数。理想的试样形状应使相对应力接近1，且使采样区的应力尽可能均匀。经仿真计算，采样区实线(图3中心区方框实线)上相对应力分布见图4。

图4 薄膜试样采样区域相对应力Fig.4 Relative stress at the sampling area

由图4可见，在5种试样形状中，带7条割缝的十字形试样的采样区内相对应力平均值为0.985，最接近1，且应力分布曲线接近直线，说明应力分布均匀。本文最终采用了如图5所示的带有7条割缝的十字形试样作为双轴张拉试验的试样。图5中，每条割缝间隔2 mm。

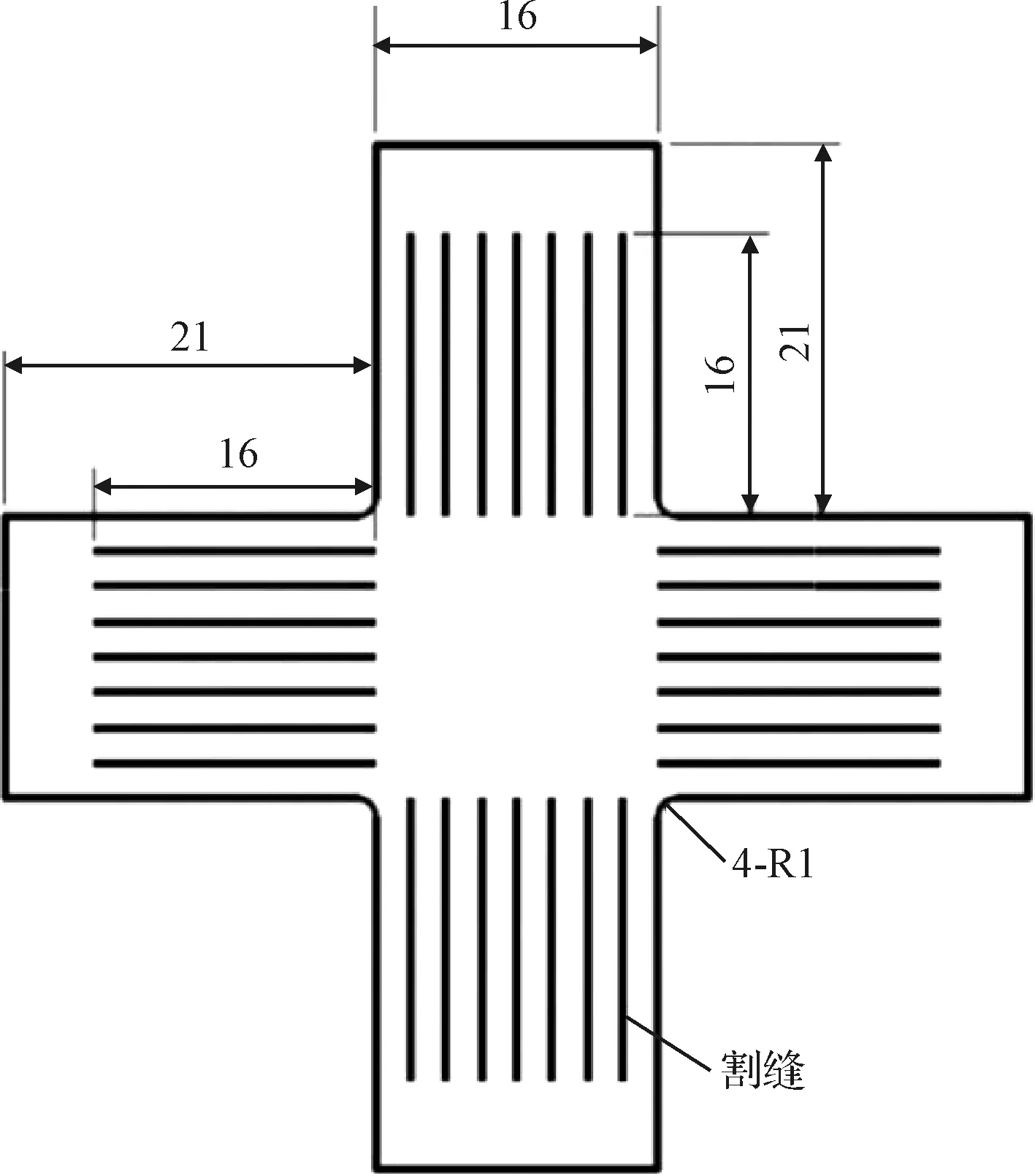
图5 带有7条割缝的十字形薄膜试样Fig.5 Cruciform membrane sample with 7 seams

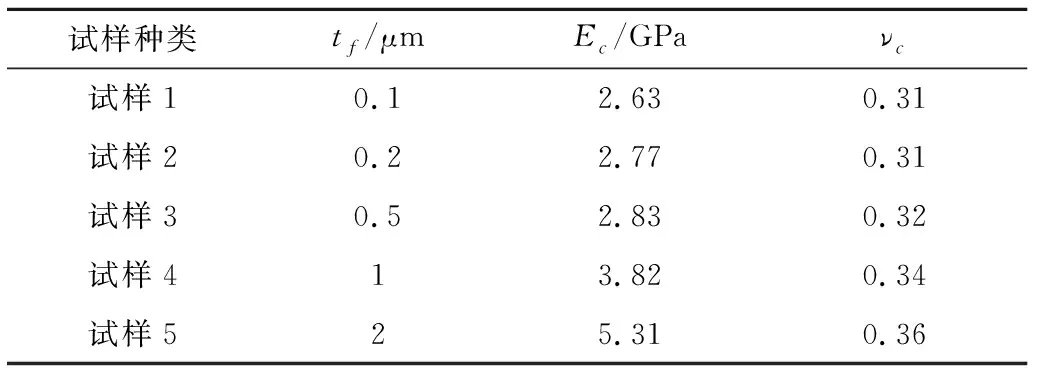
表1 双轴张拉薄膜试验结果Table 1 Biaxial extension test results

以tf为变量，用最小二乘法对表1中的Ec和νc分别进行拟合，给出的Ec和νc的拟合公式分别见图6(a)和图6(b)。

图6 Ec和νc与tf的关系Fig.6 Relations of Ec and νc versus tf

将图6(a)给出的Ec的拟合公式与式(7)进行比对；将图6(b)给出的νc的拟合公式与式(6)进行比对。根据对应关系求得：聚酰亚胺薄膜基底的杨氏模量Es=2.34 GPa，泊松比νs=0.30；铝镀层的杨氏模量Ef=41.63 GPa，泊松比νf=0.39。显然，铝镀层的力学特性明显区别于铝板材或铝带材的力学特性。

3 平面薄膜天线设计参数对应力均匀性影响分析

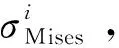
(9)

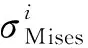
3.1 张拉系统拉力对应力均匀性的影响

参照文献[27]的算例列出图1所示平面薄膜天线单元的初始设计参数如表2所示。

表2 航天器薄膜天线初始设计参数Table 2 Initial design parameters of the membrane aperture

l和tf需根据薄膜天线的波长、孔径等性能指标来确定。在本算例中根据文献[27]设为定值：l=14 cm，tf=2 μm。Ec和νc可根据式(6)、式(7)求得。

在相关软件中，用S4R壳单元模拟薄膜平面，对含镀层薄膜单元四周施加均质边荷载。边界设置简支约束。根据结构的对称性，对单元的中心点限制x和y方向移动。网格密度为每个单元面积1 mm2。对图1所示的模型进行仿真计算，求出应力分布。计算β时选用的采样网格边长为1 cm。

控制其他可设计参数不变，改变Fx，计算结构的应力均匀性β，结果如图7所示。

图7 β与Fx的关系Fig.7 Relation of β versus Fx

由图7可知，β与拉力成线性关系。为使应力尽可能均匀，理应使拉力尽可能小。但是，张拉系统施加的拉力过小将导致薄膜刚度偏低，薄膜容易出现褶皱，进而降低薄膜天线的平面度。文献[27]根据薄膜天线的平面度要求反推出Fx不应小于2 N/m，因此本文取Fx=2 N/m为优化结果。

3.2 薄膜几何参数对应力均匀性的影响

L和ts是决定薄膜结构形状的主要几何参数。L决定了平面薄膜天线的整体尺寸，L≥l。受聚酰亚胺薄膜加工技术限制，ts一般不小于7.5 μm，不大于125 μm。根据以上限制调整设计参数，计算β，作等高线图，如图8所示。

由图8可知，当L由16 cm增加至24 cm时β小幅改善，当L由24 cm增加至30 cm时β小幅恶化。即，L对β影响甚微。而增加ts可以明显改善β，且改善幅度大致相同。例如， 当L=16 cm时，ts=125 μm时的β为ts=7.5 μm时的2.2%；当L=30 cm时，ts=125 μm时的β为ts=7.5 μm时的2.0%。

改变L和ts都会改变薄膜结构的体积V，因此β的改善需要以增加薄膜结构的体积V为代价。有必要在优化应力均匀性的同时对薄膜体积进行限制。如果限定薄膜结构体积维持在表2所示的初始状态，可以得到一条L与ts的关系曲线，见图8中虚线。根据曲线上各点的β可知，当限制V不变时，应通过增大ts、减小L来使得应力分布更加均匀。

图8 β与L和ts的关系Fig.8 Relation of β versus L and ts

如果允许V增大，则需要权衡付出质量代价与β所获得的改善的收益。因此定义评估参数β′

β′=βV

(10)

航天器薄膜结构的优化目标是以尽可能小的体积实现尽量均匀的应力分布，因此β′越小越好。

计算图8中各点对应的V，求出β′，作等高线图，结果见图9。

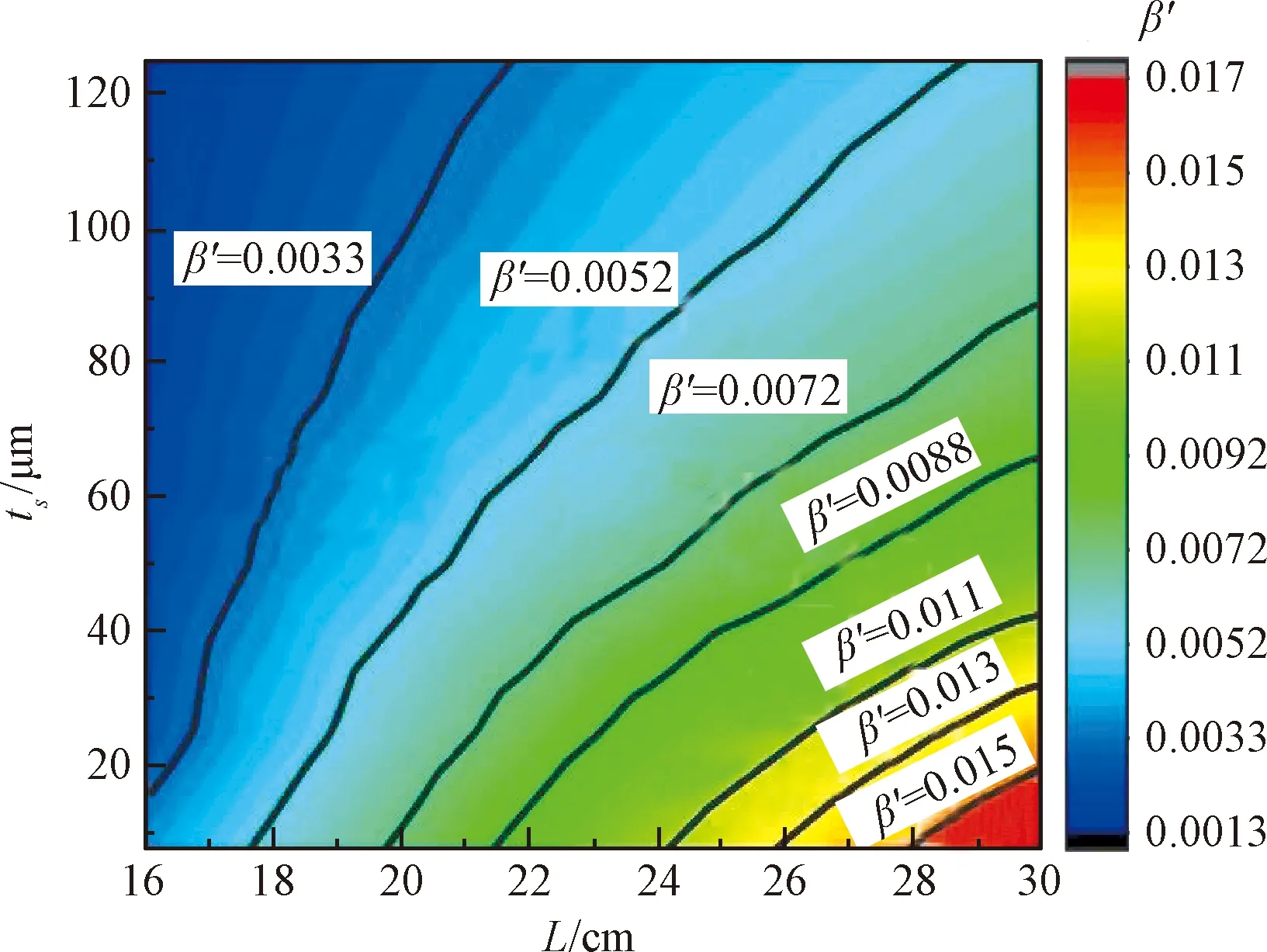
图9 β′与L和ts的关系Fig.9 Relation of β′ versus L and ts

由图9可见，L越小、ts越大，则β′越小。因此优化后薄膜几何参数取L=16 cm，ts=125 μm，此时β为优化前的7.8%。

3.3 薄膜材料参数对应力均匀性的影响

不同牌号的聚酰亚胺薄膜的杨氏模量在2.3～4 GPa范围内，泊松比都约为0.3。改变Es后计算薄膜结构的应力均匀性，结果如图10所示。

图10 β与Es的关系Fig.10 Relation of β versus Es

由图10可见，Es越大，β越小，应力分布越均匀。当Es=4 GPa时，β为Es=2.34 GPa时的58.5%。由式(7)可知，其他参数不变、仅Es增大时，Ec与Es的差值会减小，因此含镀层薄膜单元更接近均质薄膜，使得应力均匀性得到改善。

优化后航天器薄膜天线设计参数见表3。相比表2的初始状态，优化后的β为优化前的4.6%。

表3 航天器薄膜天线设计参数优化前后对比Table 3 Comparison of the design parameters before and after optimization

4 平面薄膜天线应力均匀性优化的仿真校验

为了验证经应力均匀性优化后的薄膜对蠕变行为的抑制效果，需用Bailey-Norton法则对优化前后的含镀层薄膜单元进行蠕变分析。蠕变应变εcreep与应力σ(Pa)和时间t(a)的关系为

(11)

式中：A，p，q均为常数，由试验确定。根据文献[33]的聚酰亚胺薄膜蠕变试验结果，A=4.600×10-9，p=0.720，q=-0.710。在相关软件中用式(11)进行蠕变仿真，计算优化前后的含镀层薄膜单元在恒定拉力作用下10年后的位移。仿真表明，优化前薄膜单元在工作初期最大位移为1.932 μm，工作10年后最大位移为5.382 μm，蠕变导致的位移为3.450 μm；优化后薄膜单元在工作初期最大位移为0.282 μm，工作10年后的最大位移为1.235 μm，蠕变导致的位移为0.953 μm。经过面向应力均匀性的优化，薄膜单元的蠕变为优化前的27.6%，表明本文的应力均匀性优化方法对薄膜蠕变的抑制有效。

5 结 论

经过对含镀层薄膜应力均匀化的上述分析与验证，得到研究结论如下：

(1) 用有限元法建立的薄膜单元力学模型包含了镀层，镀层区域的杨氏模量和泊松比由经典层合板理论计算获得。

(2) 设计的用于测量含镀层薄膜杨氏模量和泊松比的薄膜双轴张拉试验装置具有加载均匀的优点，试验中可保持薄膜具有较高平面度。

(3) 薄膜应力均匀性参数β与拉力大小线性正相关。为使应力均布，在满足薄膜张拉系统刚度要求的前提下，在薄膜拉力设计区间内，薄膜拉力应尽可能小。

(4) 薄膜边长对应力均匀性影响甚微。增加薄膜厚度可以明显改善应力均匀性。为了以尽可能小的薄膜质量和体积来实现尽量均匀的应力分布，薄膜边长应尽量小,薄膜厚度应尽量大。

(5) 薄膜基底杨氏模量与应力均匀性参数β负相关。增加薄膜基底杨氏模量可明显改善应力均匀性。

(6) 薄膜结构应力均匀性优化后的薄膜内应力标准差为优化前的4.6%，工作10年后蠕变导致的位移为优化前的27.6%，验证了面向应力均匀性的优化对抑制含镀层薄膜蠕变行为有效。本文的优化方法对空间大尺度含镀层薄膜天线具有普适性，但在应用该方法时，需针对具体应用场合，根据使用的基底材料、镀层材料将Es,νs和Ef,νf代入模型，给出具体的定量分析结果。