弱全局信息下月面超远距离保通行性移动规划

郭继峰，于晓强，王 平，余 欢，赵 毓

(1. 哈尔滨工业大学航天学院，哈尔滨 150001； 2. 北京空间飞行器总体设计部，北京 100094)

0 引 言

随着行星探测技术的不断发展及月球探测任务的逐渐深入，未来月球巡视器将面临诸多大范围、超远距离(>1000 km)移动探测任务场景，如月球基地选址可行性勘探、不同着陆点或月球基地间的移动探测、月球广域地质演变及资源分布的探测分析等，月球巡视器的超远距离自主移动探测能力是实现未来月球复杂探测任务的基础能力，具有很高的科学价值和应用价值[1-2]。世界各国针对具备远距离移动探测能力的巡视器相继开展了相关研究，美国NASA曾提出空间探索飞行器(Space exploration vehicle)[3]计划，通过在轮式底盘上安装小型增压舱的设计，使航天员可以进行长途探测，而不受航天服的限制。美国喷气推进实验室提出的全地形六角形地形探测者计划(All-terrain hex-limbed extra-terrestrial explorer, ATHLETE)[4]旨在开发一种六足/轮式月球巡视机器人，实现多模式下的全地形巡视，为大件货物转运及远距离运输提供支撑。日本宇宙航空研究开发机构(JAXA)和丰田汽车正在共同研发氢动力漫游车，以在少量可用能源支持下实现超过10000 km的超远距离月球巡视，进而为后续月球基地建设提供可靠保障[5]。喷气推进实验室提出了“无畏号”(Intrepid)月球大范围巡视任务[6]，目标是在四年内穿越1800 km月面区域来进行更大范围、更深层次的月球科学探测。综上可以看出，目前世界各国皆在开发具备超远距离移动探测能力的月球巡视器。

月球巡视器的移动路径规划技术作为月球超远距离探测任务中最重要的环节之一，其规划出的路径会直接影响月球超远距离探测任务的执行效率和成功率。相比于目前已有巡视器的考虑精确约束的小范围路径规划技术[7-11]，针对月面超远距离移动规划问题仍缺乏较为系统、完备的技术体系，存在以下主要问题。

(1)无高精度地图等全局精确信息

Intrepid大范围探测任务虽然制定了上千公里的巡视路线，但其是针对探测特定区域规划的固定路线，且有轨道探测器提供的极高分辨率地图数据作为支撑[6]。而未来月球巡视器面临的是任意起点/终点的超远距离移动探测任务，且部分区域没有高分辨率地图数据等信息的支撑，而缺乏高精度地图数据会使可行区域分析产生误差，使巡视器陷入现有精度地图无法发现的不可通行区域而导致超远距离移动任务失败。

(2)缺少路径可通行性考虑

目前全局规划算法着重于在一定评价标准下(如路径长度最短、消耗能量最小等)求解出一条最优路径[12-15]，而缺乏对路径可通行性和目标可达性的考虑。由于月面超远距离探测任务的高代价及高风险性，对路径的要求不单是路径最短或时间最短，更要保证路径的可通行性及探测目标地点的可达性，确保巡视器安全到达目标点是探测任务成功的必须，也是巡视器系统完备性的必要保证，需在规划技术中着重考虑。

(3)规划效率过低

当前全局规划算法的共同缺点是规划效率过低，尤其是针对超远距离转移任务中的路径规划问题，会消耗大量的搜索时间及计算资源，很难处理上千公里移动规划这类超大规模问题。

综上所述，目前全局规划技术在解决月面超远距离移动规划问题时仍存在规划完备性不足、缺少路径可通行性考虑、规划效率过低等诸多问题。受地面超远距离移动规划方式启发，本文提出月面道路拓扑网的构建设想，拟凭借其复杂道路网络的连通能力提高巡视器超远距离移动规划系统完备性和成功率。首先分析构建月面道路拓扑网的重要科学意义和应用价值，并进行月球道路拓扑网的设计构建方法研究，提出了滑动最优泊松采样算法进行网络节点设计，可使生成的网络节点分布均匀并确保道路网的密度适中且覆盖完整；同时提出了均匀邻域网络模型作为网络拓扑结构模型，并改进了A*算法的代价评估函数，连接各节点完成几何结构设计，可以使网络各路径尽量远离障碍区域，由此完成安全月面道路网的设计构建。然后进行基于月面道路网的路径规划，首先证明了基于月面道路拓扑网进行路径规划具有概率完备性，给出了影响完备性的因素，并分析了月面道路拓扑网的整体可通行概率，同时提出RPC-Dijkstra算法完成基于月面道路拓扑网的K优路径规划，为超远距离移动探测提供多条备选转移路径，可以提高巡视器超远距离移动规划系统的规划效率和完备性。最后以Apollo 11和Apollo 12两次登月任务着陆点之间进行超远距离转移任务为仿真场景，验证本方法的有效性。

1 月面道路拓扑网的设计构建

月面道路拓扑网是指具备一定拓扑结构的互连互通的通行道路网，通过构建全月通行路网，可以实现巡视器在全月可达区域内的超远距离移动路径的规划。相比于传统规划算法直接搜索大范围转移路径，构建月面道路拓扑网进行转移路径规划具有以下优势：

1)月面道路拓扑网可凭借其网络连通能力为超远距离移动规划提供多条转移路径选择，在某条路径无法通行时，可基于道路网络快速提供其他备选路径。同时当月球巡视器移动过程中遇到地图数据无法发现的不可通行区域时，可构建局部拓扑网络来寻找绕行路径，提高超远距离移动探测的可通行概率，实现更加完备高效的月面超远距离探测路径规划。

2)月面道路拓扑网构建完成后，由于月球地形环境基本不会发生变化，可长期用于大范围探测路径规划，使月面道路拓扑网成为可以信任且永久使用的有效工具。同时可基于月面道路拓扑网进行某些重点探测区域间安全转移通道的规划构建，类似我国古代重要地理要塞“河西走廊”，以供世界各国巡视器移动探测使用。

3)通过道路网规划超远距离转移路径规划速度明显高于直接在大规模地图上搜索转移路径，通过构建不同规模及不同密度的拓扑网络，可实现不同范围、不同粒度的自主探测路径规划。

对于在月面构建覆盖全月的通行道路网，相比于地球构建的公路、铁路等路网，月球具体月面环境未知，因此需要依靠分辨率有限的高程图和影像图进行地形分析。而相比于地球的城市作为路网的中途节点，月球目前没有构建道路网所需的网络节点，需要设计节点选取策略，要保证月面道路网节点尽量选在安全平坦区域，并且分布均匀，确保道路网的密度适中且覆盖完整。同时由于月球部分地区地形地貌十分复杂，如月背、两极等，因此需要构建安全道路网，确保超远距离移动路径的可行性和安全性。

综上所述，本节提出月面道路拓扑网的设计构建方法，首先提出了滑动最优泊松采样算法，可选择尽量平坦的区域中心作为构建路网所需的网络节点，同时保证节点分布均匀且覆盖完整，然后设计了均匀邻域网络模型作为网络拓扑结构，并使用改进A*算法来连接各节点完成几何结构设计，可以使道路网结构合理且连通性良好，网络中路径尽量远离障碍区域，实现全月通行安全道路网的构建。

1.1 基于滑动最优泊松采样的网络节点设计

本节对构建路网所需网络节点的选取方法进行详细介绍。首先需要保证构成道路拓扑网G=(,)的网络节点集={v1,v2,…,vn}内,各节点要选在尽量平坦、远离障碍的区域，来保证路网的安全性，同时节点需分布均匀又满足对整个任务区域的覆盖性。因此本节提出滑动最优泊松采样算法，通过设计固定大小的滑动窗口来计算任务区域内所有位置的可行区域覆盖情况，并选择滑动窗口内可行区域覆盖率满足设定的安全要求的位置作为备选节点位置来满足节点安全性要求，在满足覆盖性要求的备选位置中做最优泊松均匀采样，得到分布均匀的采样点作为构建路网所需的网络节点。

泊松圆盘采样(Poisson disc sampling)算法是一种平面随机采样算法[16]，生成的采样点满足随机且分布均匀的特性，且各点之间的距离均不小于指定的最小距离。首先设定采样点之间的最小距离为r，然后在采样范围内随机生成一个活跃采样点，在这个采样点周围的环形区域中再随机生成k个候选采样点，这个环形区域以该活跃采样点为圆心，半径从r延伸到2r。在这k个随机候选采样点中，剔除与已选定的采样点距离小于r的点，剩下的作为新的活跃采样点。如果这k个采样点都被剔除了，没有剩下任何可用的点，则将此环形区域圆心处的所选活跃采样点标记为非活跃，不再用于生成候选项。在对候选采样点剔除筛选时，使用了对角线长度为r的单元网格来加速距离检查。每个单元网格最多只能包含一个采样点，只需检查候选采样点周边固定数量的相邻单元网格即可。当所有采样点均为非活跃状态时，算法迭代结束。

图1为矩形区域内一次随机采样和泊松圆盘采样的结果对比。泊松圆盘采样生成的点集既满足随机性又满足均匀性，但这类方法有一个缺点是无法精确地控制采样点的数目和质量，尤其在月面环境这种典型的多障碍场景，泊松圆盘采样生成的点集无法保证节点是否处于可行区且尽量远离障碍。

本节提出滑动最优泊松圆盘采样算法，首先在在月面可行区域地图上设置一个边长为Rw的正方形采样窗口，采取滑动窗口的方法计算窗口内的可行区域覆盖率，选择所有可行覆盖率超过90%的窗口区域作为备选采样窗口，然后对所有备选窗口进行最优泊松圆盘采样得到网络节点集。最优泊松圆盘采样即在采样时选取可达区域覆盖率最高的备选窗口中心位置作为新的采样点，并根据设置的采样半径Rs进行节点活跃性检测，将满足条件的节点作为滑动最优泊松采样点。滑动最优泊松圆盘采样算法可以保证可行区域覆盖最优性，可以使最终采样得到的路网节点处于可行区域且尽量远离障碍，算法流程如图2所示。

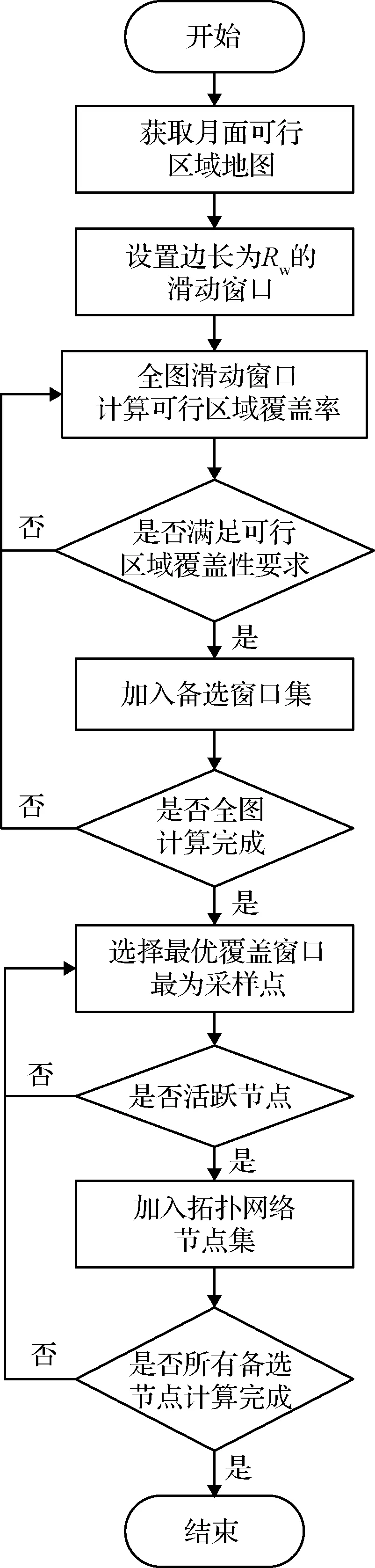
图2 滑动最优泊松圆盘采样算法流程Fig.2 Sliding optimal Poisson disk sampling algorithm flow

1.2 均匀最近邻域网络结构设计

月面道路拓扑网的网络结构是将道路网以抽象复杂网络的形式表达出来，从而进行复杂性的研究，通过拓扑结构能够对道路结构的复杂性有直观的认识理解。道路网结构一般分为拓扑结构和几何结构，拓扑结构即对道路网二维空间布局性结构的一次抽象，就是把实体抽象成与其位置、形状无关的“节点”，而把连接实体的道路抽象成“边”，进而以图的形式来表示这些点与边之间关系，拓扑结构的重点在于研究节点之间的相连关系。而几何结构表征的是点、线之间的位置关系，强调的是节点与边的位置、所构成的形状(大小)，几何结构的重点包括道路长度、道路宽度、道路方向等多种几何属性的综合影响分析。本节分别从拓扑结构和几何结构两方面进行月面道路拓扑网的结构设计。

(1)网络拓扑结构设计

复杂网络的结构可根据随机性的增加由最近邻域网络等规则网络逐渐向完全随机网络演化，而对于月面移动探测任务来说，由于需要根据地形约束设计安全、可靠、长久使用的道路拓扑网，需要将随机性降到最低，因此需要采用规则网络结构来进行网络拓扑结构设计。本节提出了均匀最近邻域网络模型作为月面道路拓扑网的结构模型，具体定义如下。

定义1：均匀最近邻域网络模型

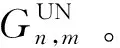
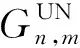
(1)

式中:vi,vj为节点vi,vj之间的平面欧氏距离;Rn为节点邻域范围，即每个节点只与距离其小于Rn的其他节点相连。

由前节滑动最优泊松采样算法可知，节点间的最小距离可由采样半径Rs控制，而相邻节点间的最大距离可由节点邻域范围Rn控制，因此可通过设计合理的采样半径Rs以及节点邻域范围Rn完成道路拓扑网的拓扑网络结构设计。通过调节采样半径Rs的大小，可以调节道路网的密度，适当的道路网密度可以保证良好的月面区域可达性以及道路网的覆盖面积，从而提高道路网的覆盖效率。而节点邻域范围Rn决定了网络的连接情况和基本结构，需要综合考虑月面道路拓扑网的设计约束及需求进行分析设计。

(2)网络几何结构设计

对于道路拓扑网的几何网络结构，需要根据网络节点的位置及拓扑关系来完成每条边的设计构造，在此过程中需要考虑月面复杂地形环境，要确保道路拓扑网的转移道路，即网络的每条边都处于月面可行区域，并避开月面主要地形障碍，因此道路拓扑网的网络几何结构设计问题即可转化为节点间的路径规划问题。

本节提出一种连接各网络节点形成安全月面道路网的路径规划方法。由于DEM地图的栅格地图特性以及月面巡视路径规划的最优性要求，本文主要研究具有最优性保证的启发式图搜索算法(A*算法)，改进了A*算法的代价评估函数，使其生成的路径尽量远离障碍区域，从而提高路网的安全性和可通过概率。

A*算法是一种启发式图搜索算法[17]，根据启发式函数f(n)来指导搜索节点的扩展，f(n)=g(n)+h(n)，其中g(n)是从起点到节点n的路径的确切代价，h(n)是节点n到目标点的剩余路径代价估计。本节定义安全启发式函数fsafe(n)来指导算法进行安全路径搜索，具体定义如式(2)所示：

fsafe(n)=g(n)+ωsafe(n)+fDiag(n)

(2)

式中：ωsafe(n)为节点n的安全代价，定义为以节点n为中心的滑动窗口内的障碍总数量，安全代价越大说明节点n周围障碍越多，其安全性越低；fDiag()为对角启发式距离函数，也可替换为欧氏距离函数或其他满足一致性条件的启发式函数。通过使用改进A*算法规划可连通节点间的安全路径，可实现节点间的远离障碍区域的路径连接，完成全月通行安全道路网的构建。

2 基于月面道路拓扑网的超远距离移动规划

在月面道路拓扑网构建完成后，可依据路网实现超远距离移动的全局路径规划。区别于传统路径规划方法在进行路径规划时根据任务设定的最优性指标规划出一条由起点到终点的转移路径，这种方法缺少对目标点可达性和路径可通行概率的考虑，无法确保月面超远距离移动任务的成功。月面道路拓扑网可凭借其复杂网络的连通能力和局部拓扑重构能力提高巡视器超远距离移动系统完备性和成功性。本节首先证明了基于月面道路拓扑网进行路径规划具有概率完备性，并给出了影响完备性的因素，然后分析了月面道路拓扑网的可通行概率，提出了RPC-Dijkstra算法完成基于月面道路拓扑网的K优路径规划，可为月面大范围移动任务一次性提供多种路径选择，实现更加完备高效的超远距离移动路径规划。

2.1 月面道路拓扑网规划完备性分析

路径规划算法的完备性是指如果规划空间中存在起点至终点的可行路径，那么算法一定可以规划出一条路径，反之如果算法规划失败，说明空间中一定不存在可行路径。基于图搜索的算法(如A*算法)皆具有完备性，但完备性算法在超远距离规划场景中应用困难，因此有些算法放宽了完备性要求以换取更高的求解效率，如基于采样的方法(RRT等)，此类算法具有概率完备性。概率完备性是指如果规划空间中存在起点至终点的可行路径，只要搜索或计算的时间够长，那么算法一定可以规划出一条路径。本节将证明基于月面道路拓扑网的规划方法具有概率完备性。

下面进行一些基本概念定义。对于离散化的地图空间可行区域F，假设可行区域内存在一条由点A到点B的长度为L的路径p[0:L]∈F，其中p(0)=A，p(L)=B，路径p上的点距离其最近障碍的距离可表示为o(t),t∈[0,L]，对于可行路径p来说，其距离障碍最小值Ro=mint∈[0,L]o(t)>0。

本节将从点A至点B之间存在可通行网络的概率与网络节点数量n的关系来分析月面道路拓扑网的概率完备性。首先给出以下定理。

定理1：假设存在一条由点A到点B的长度为L的路径p[0:L]∈F，则基于网络Gn无法在点A至点B间生成可行路径的概率Pfail的上界可表示为：

(3)

式中：α=π/(4|F|)是一个常数; |F|为任务空间可行区域面积;Ro为路径p距离障碍的最小值;n为网络节点数。

BRo/2(xi+1)⊆BRo(xi), ∀i=0,…,n-1

(4)

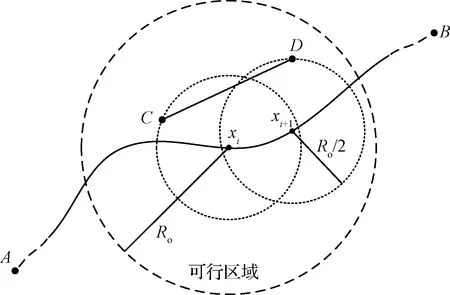
图3 沿路径p构建圆示意图Fig.3 Construct a circle diagram along path p

对于有n个节点的网络Gn来说，若沿路径p构建的x个圆BRo/2(pi),i=1,…,x，每个圆中均至少含有一个网络节点，则这些节点及节点之间的边均处于可行区域中，说明基于该网络一定可以规划出由点A到点B的可行路径。若其中存在不包含网络节点的圆，则基于该网络的规划有可能失败。本节定义事件1：沿路径p构建的x个圆BRo/2(pi),i=1,…,x，中存在不包含网络Gn节点的圆的概率为P1，事件2：圆BRo/2(pi)中不包含任一网络Gn节点的概率为P2。由于网络Gn的节点{v1,v2,…,vn}所处位置相互独立，因此有：

P2=[1-SBRo/2(pi)/(|F|)]n=

(5)

则基于网络Gn在点A至点B间规划失败的概率Pfail，有：

(6)

而基于如下式所示的不等式关系：

1-x≤exp(-x), ∀x≥0

(7)

可将式(6)转化为

(8)

定理1证毕。

由定理1可得，基于月面道路拓扑网在两点间搜索出可行路径的成功概率Psucc满足：

1-a·exp(-bn)

(9)

(1)规划距离，即可行路径长度L，规划距离越长，整体任务难度越高，规划成功率越低。

(2)环境复杂度，即可行路径距离障碍的最小值Ro，Ro越小，环境复杂度越高，规划成功率越低。

(3)网络节点数，网络节点数越多，对整个任务区域的覆盖性就越强，基于该网络规划的成功率就越高。

综上，对于一个确定的规划环境或规划任务，其规划距离及环境复杂度是固定的，即使对于未知动态的任务其也是一个有界的数值，而网络节点数可以根据任务动态调整，且基于月面道路拓扑网规划成功的概率随网络节点数增加而增加，极限条件下当网络密度足够大时，可保证基于月面道路拓扑网的路径规划成功率趋近于1，因此利用月面道路拓扑网进行月面超远距离移动路径规划具有概率完备性。

2.2 月面道路拓扑网可通行概率分析

月面地形条件是影响路径可通行性最重要的因素，在保证地形特征提取精度精准可靠的条件下，可以直接依靠计算提取的地形特征进行路径可通行性分析。由于DEM地图是获取月面地形特征的主要方式，而目前可公开获取的具有较高分辨率及数据精度的全月数据集主要包括中国嫦娥二号拍摄形成的CE2TMap2015全月数据集以及美国SLDEM全月数据集，其最大分辨率分别为20 m及59 m，该分辨率地图不足以获取月面精细准确的地形特征，使用有限分辨率DEM地图计算得到的地形特征及可通行区域等信息会存在一定误差，因此需要针对不同分辨率地图分析不同区域的地形计算误差及可通行概率。

本节首先分析单条路径的可通行概率，其可以表示为该路径途径的月面区域的最小可通行概率，而月面不同区域的可通行概率将主要考虑该区域坡度的影响，坡度越小，可通过性越高，但同时还需要考虑使用不同分辨率DEM地图进行地形提取所带来的误差的影响，误差越大，对地形描述越不准确，将会一定程度上降低地形的可通过概率。因此需要对有限分辨率DEM地图下的坡度计算误差进行分析。

月面地形特征提取精度与DEM地图误差及分辨率直接相关，而DEM地图误差固定且连续，对地形特征提取影响不大，但DEM分辨率不同，所提取的地形特征也会发生改变，从而对地形特征分析造成一定的影响。现有文献研究表明，以坡度为例，根据不同分辨率DEM地图提取的坡度数据，随着DEM地图分辨率的降低，每个分辨率包含的地形信息更加概括，对不同区域地形细节的表达能力逐渐降低，坡度提取误差会逐渐增大。文献[18]对平均坡度与DEM地图分辨率间的关系进行分析，结果表明，针对所有地形，随着分辨率降低地形平均误差(记作Ea)均增大，并且地形起伏程度越高，这种增加越明显，说明分辨率降低总体造成坡度的误差数值增大。该文献根据在黄土高原试验样区高程数据采样并对Ea误差进行了回归分析，得到Ea误差与DEM分辨率及平均坡度的关系模型如下所示：

Ea=(0.514s-0.002)ln(r)-(0.285s+0.004)

(10)

式中:r为DEM分辨率；s为分析区域的平均坡度。由此可得地形平均误差与DEM分辨率与区域平均坡度之间的对应关系。

本节将某分辨率地图中某栅格的可通行概率Ptrans(i)建模为该栅格内真实地形全部满足巡视器运动能力的概率，首先将栅格内真实地形分布建模为正态分布，均值μi为该分辨率地图计算的地形坡度，标准差为该区域该分辨率地图对应的地形计算误差，建立该分布后，计算该栅格内坡度全部小于巡视器最大爬坡能力smax的概率即为该栅格的可通行概率。

(11)

在分析完单条月面规划路径的可通行概率后，可进行月面道路拓扑网的整体可通行概率分析。对于网络G及其任意两个节点对vi，vj之间存在的可行路径数量Nij，假设每条路径均存在一个通行概率Ptrans(i)，则可采用概率分析理论计算月面道路拓扑网任意节点对vi，vj之间的可通行概率Ptrans(i, j)如下式所示：

(12)

式中：Ptrans(i)∈[0,1]为月面道路拓扑网中节点对vi，vj之间的每条路径的可通行概率。

对于网络G，网络内任意两个节点对vi，vj之间存在的可行路径数量为[19]：

(13)

式中：lmax为节点vi，vj之间最长可行路径限制，可人为设定或根据网络节点数量计算。

下面分析网络节点数量及网络边数对可行路径数量的影响。当网络节点数量n增加时，其邻接矩阵A内的非零元素增加，Nij增大。对于网络G，令网络G′表示对网络G中随机增加一条边e后的网络，则网络G′中任意两个节点对vi，vj之间存在的可行路径数量Nij(G′) =Nij(G)+N′ij，其中，Nij(G)是不经过边e的可行路径数量，即没有添加边e的原网络G的路径数量，N′ij为节点对vi，vj之间经过边e的可行路径数量，显然N′ij≥0，因此网络任意两节点间可行路径数量满足网络节点数量及边数量的单调性。

因此月面道路拓扑网任意节点对vi，vj之间的可通行概率Ptrans(i, j)与节点间可行路径的数量成正比，即Nij越大，总体可达性Ptrans(i, j)越大，而可行路径的数量Nij与网络节点数量n，网络边数皆成正比。由此可见，基于月面道路拓扑网进行月面超远距离路径规划相比于传统单条最优路径规划方法可提高路径的可通行概率，同时在网络密度变大时，即网络节点和边的数量增加时，月面道路拓扑网的可通行概率增加，极限条件下当网络密度足够大时，可保证月面道路拓扑网的整体可通行概率趋近于1，也间接证明了利用月面道路拓扑网进行月面超远距离移动路径规划具有概率完备性。

2.3 考虑重复路径代价的K优路径规划

本节进行基于月面道路拓扑网进行超远距离探测K优路径规划的方法研究。首先进行K优路径规划问题的定义，设Pij是网络G中节点vi和vj间所有可行路径的集合，则最优路径规划问题的定义就是在Pij中寻找一条距离最小的路径p′，即在网络G中寻找一条路径p′，满足p′∈Pij，且对于任意路径p∈Pij,p≠p′，都有路径长度dp′≤dp。而K优路径规划问题是最优路径规划问题的扩展，目的是寻找包括最短路径、次短路径直至第k短路径的集合，即在网络G中寻找路径集合P′={p′1,p′2,…,p′k}，满足P′∈Pij，且对于任意路径p∈Pij,p∉P′，都有dp′i≤dp，同时对于1≤i≤k，有dp′i≤dp′i+1。

对于无向图中从一个顶点到其余各顶点的最短路径规划问题，可使用Dijkstra算法[19]进行求解。经典Dijkstra一次只能搜索出一条起点至终点的最短路径，为了求解无向加权图G中的K优路径规划问题，本节提出基于重复路径代价Dijkstra (Repea-ted path cost Dijkstra, RPC-Dijkstra)的K优路径规划算法，引入路径重复度及重复路径代价因子的概念，在最优路径规划完成后，将与最优路径重复的路径段增加重复路径代价，使无向图中重复路段对应边的权重增加，从而使算法再进行次优路径规划时产生与最优路径差异化的路径结果，为超远距离移动探测提供多条备选转移路径。

RPC-Dijkstra求解流程如图4所示，首先基于原权重图G利用Dijkstra算法规划最优路径，将此最优路径加入K优路径集合P′，然后为当前最优路径添加重复路径代价，将最优路径途径边的权值乘以重复路径代价因子ωRP(ωRP>1)，根据权值更新后的图G规划下一最优路径p′i+1，然后计算p′i+1与路径集合P′中路径的重复度。本节定义图G中路径pi相对于pj的路径重复度Rij为pi和pj相同边的数量与路径pj长度的比值，代表两条路径的重复情况。若路径p′i+1与集合P′中路径的重复度均满足要求，即均小于设定的最大重复度，则将此路径p′i+1加入P′，然后继续增加重复路径代价，直至找出全部k条最优路径。

图4 RPC-Dijkstra算法求解流程Fig.4 Solution flow of RPC Dijkstra algorithm

此外，由于月面道路拓扑网是基于分辨率有限的DEM地图构建，不能保证巡视器在真实转移过程中全程路径的可行性，如基于超远距离全局规划结果转移途中发现实际不可通行区域，则需要转移路线的重规划，通过在无法通行点至下一网络节点之间通过构建密度更大的局部拓扑网络，可对月面道路拓扑网进行更新，生成新的可通行路径，这样即可快速实现转移路径重规划，避免重新搜索超远距离全局路径，极大的缩小了重规划所需的时间及计算资源。

3 仿真校验分析

3.1 仿真场景

本文拟在Apollo 11和12两次登月任务的着陆点之间进行超远距离转移任务，选取Apollo 11及Apollo 12两次任务的着陆点作为超远距离移动探测任务的起止点。首先获取任务区域的DEM数据，由于嫦娥二号全月地形数据产品在空间分辨率、全月覆盖率、定位精度和地貌结构细节表达等方面相比其他全月地形数据具有明显优势[21]，所以本文采用嫦娥二号CE2TMap2015数据产品中的DEM-50 m数据集进行月面可达区域分析，分析区域面积达2207.2 km×871.3 km。提取任务区域高程信息如图5所示。

图5 Apollo任务区域DEM地图Fig.5 DEM map of the Apollo mission area

3.2月面道路拓扑网构建仿真

下面对月面道路拓扑网构建方法进行仿真分析。首先对该任务区域进行最优泊松圆盘采样，选取构建路网所需网络节点，设置采样滑动窗口大小为20 km×20 km，设置采样半径Rs=30 km，阿波罗任务区域进行网络节点选取结果及其泊松圆盘覆盖情况如图6所示，共采样网络节点668个，采样节点窗口内可达区域覆盖率最高100%，最低95.2%。由图6可以看出，网络节点基本处于安全平坦区域，最优泊松圆盘采样结果密度适中且对整个任务区域覆盖性很好，使得路网的覆盖效率达到最大。

然后进行月面道路拓扑网的结构设计仿真，基于本文所提出的网络拓扑结构及几何结构设计方法进行网络结构设计。本节设置节点邻域范围Rn= 45 km。同时设置改进A*算法的安全代价函数的窗口大小为1 km×1 km，即算法的安全代价权重考虑该范围内的障碍总数量，在阿波罗任务区域路网构建结果如图7所示，网络参数统计信息如表1所示，可以看出，本文构建的月面道路拓扑网可以完整覆盖Apollo任务区域，网络连通性良好，可以保证较高的月面区域可达性以及网络覆盖效率。同时，基于月面道路拓扑网的转移路径会尽量远离多障碍区域，从而提高了路网的安全性和可通过概率。

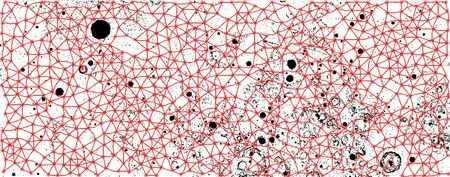
图7 Apollo任务区域月面道路拓扑网构建结果Fig.7 Results of safety road network construction in the Apollo mission area

表1 月面道路拓扑网网络参数统计Table 1 Statistics of lunar road topology network parameters

3.3 基于月面道路拓扑网超远距离路径规划仿真

本节进行基于月面道路拓扑网的超远距离路径规划仿真，在路网中进行最优路径搜索，选取Apollo 11和Apollo 12两次任务着陆点为仿真的起点终点，模拟超远距离移动路径规划任务。设置最优路径数量k=5，重复路径代价因子ωRP=1.2，最大可接受路径重复度为80%，所得K优路径规划结果如图8所示，指标参数对比如表2所示，可以看出RPC-Dijkstra算法能够实现基于月面道路网的K优路径规划，5条路径在路径长度、窗口可行区域覆盖率及可通行概率方面各有优势，综合考虑5条路径的整体可通行概率为99.99%，可保证超远距离移动路径的安全性及可通行性。

图8 Apollo任务区域超远距离路径规划结果Fig.8 Large scale path planning results of the Apollo mission area

表2 K优路径规划路径指标参数对比Table 2 Path index comparison of K-optimal path planning

然后以路径1为例，本节对超远距离移动规划路径的全路程坡度信息及路径节点窗口内障碍区域覆盖率进行统计处理，结果如图8及图9所示，图中阴影部分为原始数据，实线为经过平滑后的数据。可以看出基于月面道路拓扑网规划的移动路径整体坡度较为平缓，全程坡度最大值约为10°，且路径全程1 km×1 km窗口内障碍覆盖率很低，在中段及后段高原区域的障碍覆盖率有所增长，但整体障碍覆盖率在5%以下，说明本文所构建月面道路拓扑网可以实现移动路径远离多障碍区域，从而提高超远距离移动探测的安全性及可通过概率。

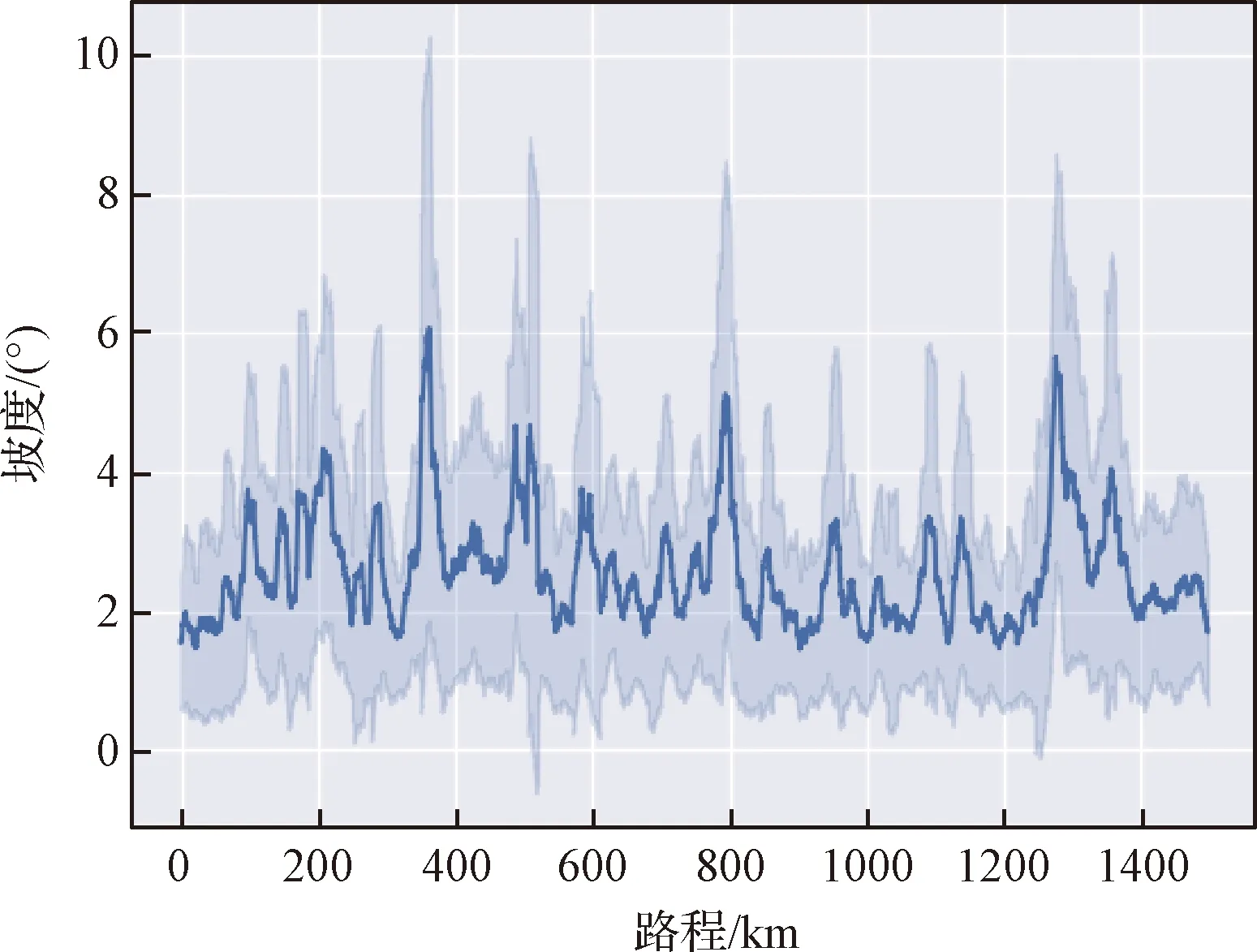
图9 月面道路网规划路径的坡度变化信息Fig.9 Slope change information of planned path of lunar road network

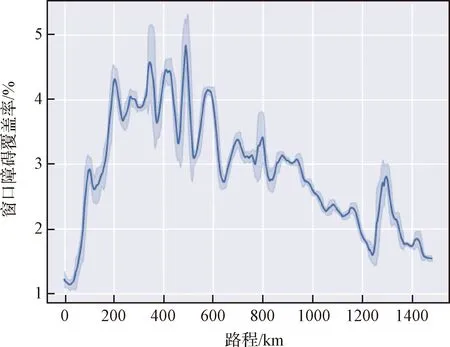
图10 月面道路网规划路径的障碍覆盖率Fig.10 Obstacle coverage of planned path of lunar road network

本节同时将基于月面道路拓扑网的路径规划与标准A*算法、JPS算法[22]进行了性能对比，结果如表3所示。可以看出，基于月面道路拓扑网的路径规划虽然路径长度略高于其他两个算法，但路径平均坡度及平均障碍区域覆盖率明显优于其他算法，表明月面道路拓扑网的构建可以提高超远距离移动路径的安全性。同时，由于本节是基于已经构建完成的月面道路拓扑网的路径规划，路径搜索时间明显优于其他算法，可以极大提高超远距离全局路径搜索的计算效率。

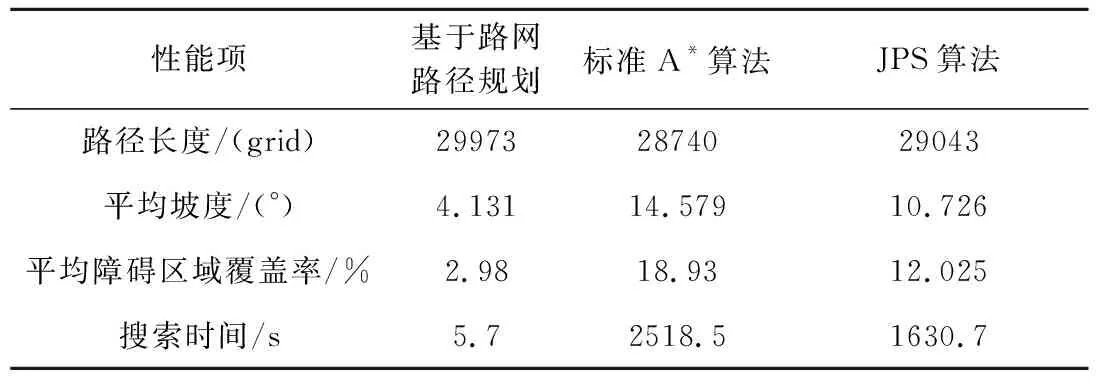
表3 不同算法的性能表现对比Table 3 Performance comparison of different algorithms

4 结 论

本文基于月面道路拓扑网的构建设想提出了一种弱全局信息下月面超远距离保通行性移动规划技术，得出以下主要结论：

1) 提出了月面道路拓扑网的构建设想，分别针对节点及结构设计提出了网络设计方法，仿真结果表明本文构建的道路网密度适中且对整个任务区域覆盖性很好，网络中各移动路径会尽量远离多障碍区域，从而提高了月面道路网的安全性和可通过概率。

2) 进行了基于月面道路拓扑网的超远距离保通过性路径规划，首先证明道路网规划的概率完备性，并分析了月面道路网整体可通行概率，同时提出了RPC-Dijkstra算法实现基于道路网的K优路径规划。仿真表明基于月面道路拓扑网可实现上千公里级的月面探测路径规划，网络可通行概率明显高于单条路径，同时路径的安全性和搜索时间明显优于其他算法。

本文旨在通过月面道路拓扑网的设计构建实现更加安全完备的月面超远距离移动探测任务，具有重要的概念创新和理论研究意义，有一定的工程应用潜力，可为未来月球探测任务提供有价值的发展建设思路。