航天器姿态机动规划技术研究进展

徐 瑞，朱 哲，李朝玉，范宇麒，朱圣英，尚海滨

(1. 北京理工大学宇航学院， 北京 100081； 2. 深空自主导航与控制工业和信息化部重点实验室(北京理工大学)， 北京 100081)

0 引 言

航天器在轨运行或深空探测过程中，需要执行姿态机动。姿态机动是航天器从当前姿态转换到目标姿态的再定向过程[1]。而姿态机动规划是指对姿态机动过程中空间上的姿态路径以及时间上的角速度、控制力矩等运动学、动力学参数进行综合规划求解，生成满足各种约束的姿态机动路径，本文中也称作姿态规划。姿态规划是姿态控制系统中的重要环节，如图1所示，在航天器自主姿态控制系统中，姿态测量敏感器获取姿态和角速度参数在内的测量数据，反馈输出给姿态规划和控制模块。姿态规划根据输入的姿态约束和优化目标，通过约束处理和指标优化生成姿态机动路径，以控制指令形式传递给姿态跟踪控制模块，进一步由执行机构执行姿态机动轨迹。

图1 航天器自主姿态控制系统结构Fig.1 Structure of spacecraft autonomous attitude control system

针对无指向约束下的姿态机动问题，采用姿态控制方法一般可得到有效的解决。多年来广大学者在姿态控制领域进行了深入研究，采用经典PID控制、根轨迹法和频率响应法、H2/H∞控制等方法对姿态控制器进行设计，可以有效地处理小角度姿态机动问题。近年来对滑模变结构控制、模型预测控制、鲁棒控制和最优控制等多种现代控制理论的研究，使大角度姿态机动控制亦得到快速发展。然而在航天任务中，航天器姿态机动需要满足一系列姿态指向约束，例如，强光天体(如太阳)的方向矢量不能进入相机和恒星敏感器等光学敏感器元件的视场；执行目标探测任务时，天线要保持通信指向同时相机跟踪目标等。在哈勃空间望远镜、卡西尼号以及深空一号等探测任务中都考虑了复杂姿态指向约束[2-4]，它们限制了航天器在姿态空间的机动路径可行域。

在综合考虑复杂多约束和能量消耗、机动时间等优化指标的情况下，单独采用姿态控制方法难以满足约束和求解姿态机动路径，姿态规划技术成为航天器姿态机动领域的重点研究方向之一[5-8]。在姿态规划中综合考虑各种复杂约束和优化目标并通过规划方法求解得到姿态机动路径、运动学动力学参数，这样既可以满足多种姿态机动的约束，又能够减少姿态机动的资源消耗和提高姿态控制精度。

姿态规划技术的应用对于航天器姿态机动任务具有如下的意义：

(1)姿态规划能够有效处理多轴多约束，增强航天器在复杂空间环境限制下的姿态机动能力；

(2)姿态规划生成参考路径，再通过跟踪控制执行轨迹，能够减少对复杂姿态控制方法的要求，降低控制系统复杂性并提高控制精度；

(3)航天器通过姿态规划方法优化姿态机动路径，提高姿态机动解的全局最优性；

(4)姿态规划能够有效实现工程应用中的多种任务目标,处理模型误差或者环境不确知等问题，提高航天器满足多种任务需求的多目标优化能力和姿态机动鲁棒性；

(5)姿态规划技术能够为航天器实现更高层次的自主运动规划和自主智能运行提供关键技术支撑。

姿态规划问题求解的难点在于，不仅需要考虑光学敏感元件或太阳帆板等载荷的姿态指向约束，还要考虑姿态动力学约束和有界约束。姿态指向约束是航天器的外部环境约束，限制了航天器姿态机动的可行解区域；姿态动力学约束和有界约束是航天器的内部约束，即航天器姿态机动遵循特定的姿态动力学模型，同时执行机构输出的控制力矩和姿态敏感器的测量角速度受到限制。在航天器姿态机动过程中，外部环境的变化会产生不同的姿态指向约束，当由此引发的复杂姿态指向约束和航天器自身动力学约束耦合在一起时，姿态机动路径难以求解。对此类情况的可行解规划方法是当前姿态规划技术研究的一个重要方向。

姿态规划技术在轨适用性可能受到如下性质的影响：对复杂多约束的处理能力有限；输出解的随机性较大难以在轨应用；计算效率较低占用过多星上资源。因此，姿态规划技术的在轨应用需要快速高效地处理复杂多约束的能力的支持。同时，航天器在执行姿态机动任务时通常需要优化燃料消耗或姿态机动时间。在考虑这类优化目标的情况下，姿态规划技术需要兼顾满足复杂约束和计算高效性、规划结果的确定性，以利于星上应用。总而言之，提高规划计算效率同时对燃料消耗和机动时间进行优化，是姿态规划中迫切需要解决的一个问题。

目前，国内外研究人员根据姿态规划问题建模、路径求解、优化等不同角度，对航天器姿态规划问题进行了深入研究。从上述描述可以得出，对规划问题的复杂约束处理是影响姿态规划技术方法特点和应用性能的核心因素。本文根据不同的姿态规划方法中的约束处理方法将航天器姿态规划技术分为约束评价规避方法、约束简化松弛方法、约束几何规避方法、约束解析满足方法四大类，如图2所示。

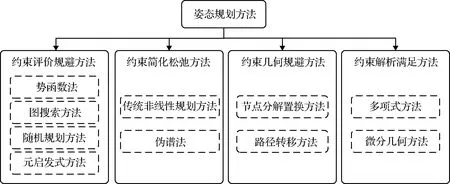
图2 姿态规划技术方法分类Fig.2 Categorization of attitude planning methods

约束评价规避方法包括势函数法、图搜索方法、随机规划方法和元启发式方法。势函数法发端于20世纪80年代，于1994年首次应用于航天器姿态规划[9]。图搜索方法以A*算法为典型，发表较早，但直到2013年才应用于姿态规划问题[10]。随机规划方法以概率路线图法(1996年)[11]和快速搜索随机树方法(1999年)[12]为典型。元启发式方法作为一种特殊的约束评价规避方法于2014年[13]开始应用于姿态规划问题。约束评价规避方法设计启发式评价函数，当姿态空间中状态节点通过局部搜索或随机生成进行路径扩展时，采用评价函数估计并选择节点，连接节点生成路径实现对约束的规避。总的来说，约束评价规避方法能处理复杂指向约束，但处理有界约束和姿态动力学约束时可能因方法不确定性使得星上独立应用可靠性不足。约束评价规避方法是一种非最优解姿态规划方法。

约束简化松弛方法从传统非线性规划方法到伪谱法及其多种变型，经历了长期、持续的发展。约束简化松弛方法将多约束姿态机动规划问题转化为一个非线性规划问题，相比于使用非线性规划工具直接求解，对原问题进行了适当的简化变形。该类方法能引入优化目标，但对复杂约束处理效果不足，鲁棒性一般。其中，伪谱法将最优控制问题离散化转变为非线性规划问题，采用正交多项式描述最优解曲线，从而对多项式系数进行数值求解。伪谱法的应用优势在2007年得到航天任务在轨验证[14]，但选择不同类型的伪谱法会得到不同的计算效率。

约束几何规避方法最早于1992年用于航天器姿态机动可行路径求解[15]。该方法利用空间矢量的几何关系设计路径上节点的指向约束检测和规避方法，通过建立映射关系，在二维平面上处理三维指向约束，中间路径节点使用球面几何距离标定，得到姿态规划序列。近年来该方法获得了多方面拓展研究，能够处理优化问题，复杂约束处理能力较强，且计算效率较高。

约束解析满足方法采用连续的参数化函数曲线来表示航天器的姿态机动路径解析解，最早发展于多项式方法(2005年)[16]。这种方法通过求解或者优化少量的路径参数，即可实现问题求解，因此约束解析满足方法计算效率较高。但是路径参数的变化对姿态路径的改变有限，难以有效地满足复杂多轴指向约束。

除此之外，部分姿态规划方法仅处理特殊姿态规划问题，如约束监测法；还有的姿态规划方法利用特殊数学思想对规划模型进行简化，如基于函数空间梯度的路径优化方法。这些方法一般对姿态机动约束处理具有一定局限性。表1展示了图2中主要的姿态规划方法的不同特点及各自的局限性。

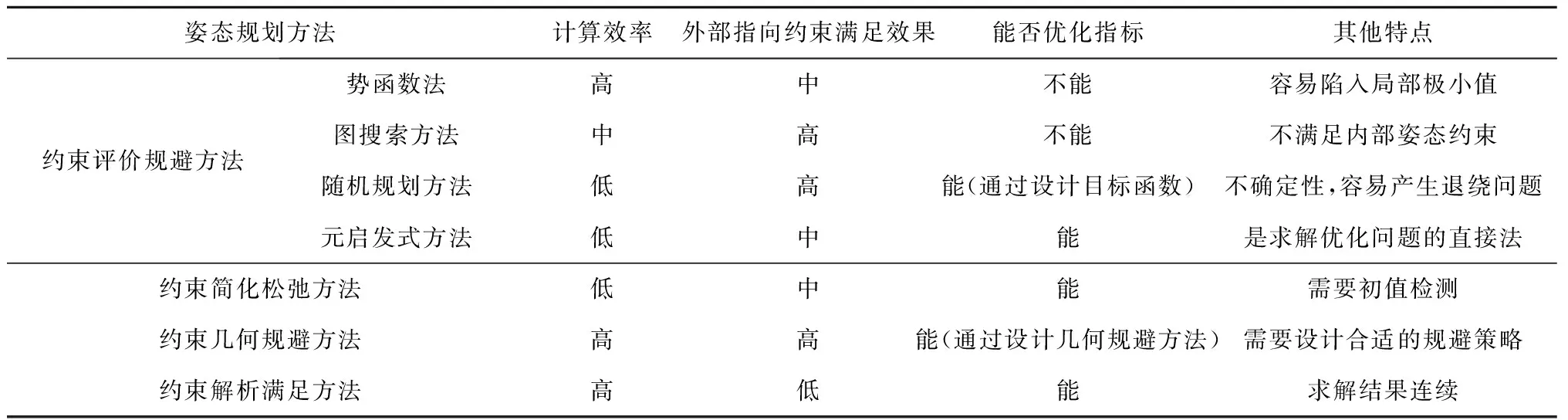
表1 姿态规划方法比较Table 1 Comparison of different attitude planning methods

航天器姿态机动规划技术能够减少航天器姿控系统对复杂姿态控制方法的需求和依赖，丰富并增强复杂姿态机动任务场景下的机动执行能力，使航天器具备自主规划和运行能力。

1 航天器姿态机动规划模型

航天器执行姿态机动任务需要姿态规划技术规划出合理的姿态机动路径，该路径需要满足由航天器内部特性及外部环境决定的多种复杂约束。航天器姿态机动规划建立在约束表达和规划模型的基础之上。

在姿态规划技术中，刚体航天器的姿态运动学方程通常采用四元数表示如下：

(1)

式中：q=[q0,q1,q2,q3]T，四元数表示一个旋转的旋转轴和旋转角度，单位四元数满足q2=1;ω=[ω1,ω2,ω3]T表示在本体系下的惯性角速度。

航天器约束分两大类：内部特性带来的姿态约束和外部环境产生的姿态指向约束，分别称为内部姿态约束和外部姿态约束。在航天器姿态机动过程中这两类约束会耦合在一起，限制姿态机动的可行域。

航天器内部姿态约束主要包括动力学约束和有界约束。全驱动的刚体航天器能提供三轴姿态控制力矩，其满足的动力学约束如下：

Iω=T-ω×Iω

(2)

式中：I=diag(I1,I2,I3)表示航天器相对本体系的惯量矩阵；T=[T1,T2,T3]T表示本体系下的控制力矩及其分量；ω×是ω的叉乘矩阵：

(3)

有界约束也即不等式约束，姿态规划中主要包括控制力矩和角速度有界约束。航天器在姿态机动任务中执行机构输出力矩幅值有限，形成了控制力矩的约束边界：

|ui|≤γ1,i=1,2,3

(4)

式中：γ1表示航天器控制力矩的幅值。

同时，航天器的角速度敏感器有一定的量程，航天器的角速度需要保持在仪器测量范围内，由此形成了角速度约束边界：

|ωi|≤γ2,i=1,2,3

(5)

式中：γ2表示航天器角速度的幅值。

外部姿态约束是指航天器在姿态机动任务时，其本体或可动部件的姿态受到在姿态空间中指向的约束，这类约束缩小了航天器姿态机动的可行域，也称作姿态指向约束。姿态指向约束由于强光天体进入相机视场、天线偏离通信目标等而被违反时，航天器的导航定姿、科学观测或通信传输能力将遭到损坏，影响任务正常执行。姿态指向约束包括禁忌指向约束和强制指向约束。

在航天器姿态机动过程中，相机必须“禁止”非目标的强光天体进入视场角，类似这种规避特定指向的约束称为禁忌指向约束[4,15,17]，简称禁忌约束。图3为航天器禁忌指向约束示意图，rg1,rg2表示两个光敏元件在本体系下的视场中心方向矢量，rI表示禁忌指向(如强光天体)在惯性系下的方向矢量。

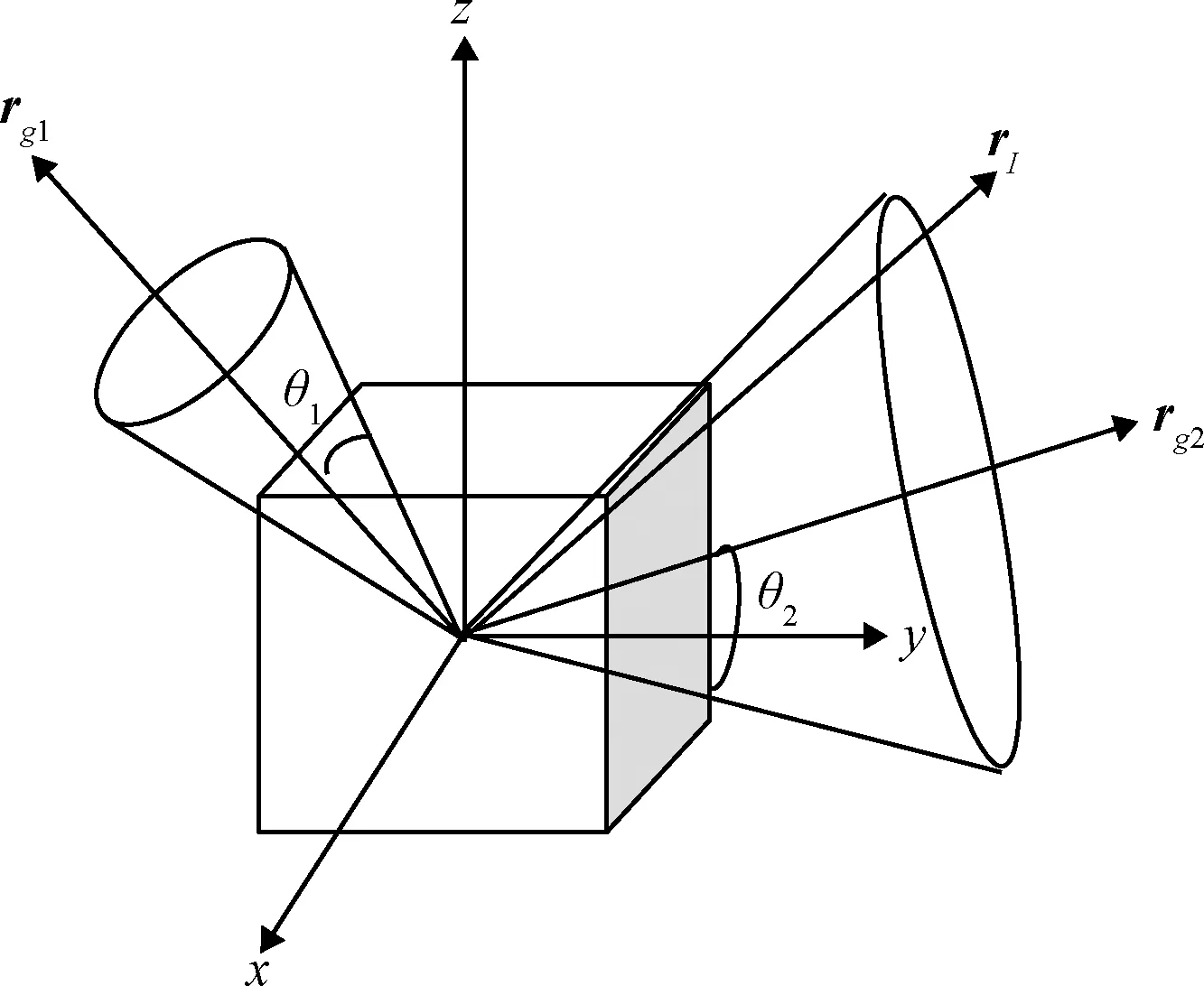
图3 航天器禁忌指向约束示意图Fig.3 Diagram of spacecraft keep-out constraints

禁忌指向约束要求禁忌指向和光学敏感载荷的视场中心方向矢量夹角不能小于视场角，表示为：

(6)

式中：i=1, 2;CIB与CBI表示本体系与惯性系之间的转换矩阵。

特别地，将余弦矩阵展开，可以将指向约束表示为二次型[17]：

qTKCq≤0

(7)

式中：

(8)

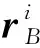
图4 航天器强制指向约束示意图[19]Fig.4 Diagram of spacecraft keep-in constraint[19]

(9)

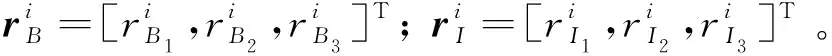
在姿态任务中，航天器不仅需要满足上述复杂约束条件，还需要进一步地实现姿态机动快速和低能量等目标。综合考虑航天器姿态机动过程中的复杂约束和优化目标，航天器姿态机动规划模型如下所示：

(10)

式中：p(x)表示姿态任务的目标优化函数，如姿态机动时间最短或能量消耗最低。航天器姿态规划技术基于上述姿态机动规划模型进行规划求解，得到满足多种约束和目标的姿态机动路径。

2 航天器姿态规划技术研究现状

航天器姿态规划技术对姿态机动问题的复杂多约束进行处理，建立并求解规划模型，生成姿态机动的执行路径。约束处理方法体现了姿态规划技术的核心思想，据此可对航天器姿态规划技术作出分类及进一步划分。

2.1 约束评价规避方法

约束评价规避方法运用于姿态规划时，首先将动力学方程的姿态参数空间离散化，使用启发式评价函数对网格化节点或随机节点进行估计，再通过搜索算法或随机扩展求解得到满足指向约束的姿态机动路径，该路径即基于评价函数的启发式路径解。姿态空间通过势函数构造势能场描述姿态空间及指向约束时，采用势函数法；姿态空间进行节点网格划分时采用图搜索方法；姿态空间中节点随机扩展时采用随机规划方法。特别地，对于姿态规划的优化方法，当约束评价规避方法中姿态参数空间的搜索模型以特定自然现象为模拟，实现局部搜索和随机扩展的平衡时，认为其构造的启发式是广义的、泛化可用的，称为元启发式方法，详见2.2.3节。

2.1.1势函数法

势函数法(或人工势场法)由Khatib[20]提出，其基本思想是根据目标和指向约束对姿态机动的影响设计启发式的势函数，将姿态空间构造为势能场，实现目标处吸引、禁忌约束处排斥的效果。势函数法用于姿态规划有两个步骤，一是势函数的设计，势函数包括吸引势函数和排斥势函数，用于产生描述机动路径过程中目标姿态和指向约束的吸力和斥力；二是姿态控制器的设计，需要考虑有界约束并回避势函数的局部极小值。势函数法的构造示意图如图5 所示。

图5 两个禁忌约束下的势函数构造示意图[9]Fig.5 Diagram of potential function with two keep-out constraints[9]

针对光学载荷视场需要规避太阳的姿态机动问题，McInnes[9]采用姿态欧拉角的描述方式并且首次引入势函数法，通过排斥势函数产生高势能从而规避禁忌约束，同时运用李雅普诺夫(Lyapunov)第二法，得到控制力矩的解析表达式。针对星敏感器需要规避太阳的姿态机动问题，Wisniewski等[21]利用势函数法规避指向约束，同时实现了对四飞轮驱动航天器的最优控制力矩分配。随后的研究逐渐将势函数法的应用范围扩展到姿态指向约束、有界约束、随机干扰和抗退绕等方向。Lee等[22]在对单位四元数空间内姿态指向约束集合的凸参数化的基础上，设计了凸对数势函数，处理姿态指向约束。Shen等[23]采用单位四元数的姿态描述方式设计了凸二次势函数，在不显式使用速率反馈的基础上实现了禁忌约束下挠性航天器的姿态机动。进一步地，Shen等[24]在采用凸二次势函数规避姿态指向约束的基础上，又设计了凸对数势函数来处理角速度有界约束，最后将两种势函数与滑模控制方法结合得到自适应的非线性姿态控制律。Chen等[25]应用参数选择方法，改进了单位四元数表示的排斥势函数的存在条件，而后结合反步法，研究了姿态指向约束、输入饱和以及随机干扰同时存在下的姿态机动问题。为了解决四元数双值性所带来的退绕问题，Hu等[26]在姿态指向约束的势函数的基础上加入抗退绕的姿态误差函数，以满足姿态指向约束。

势函数法计算简单，实时性好，路径平滑，易于应用，但是存在以下缺点：

1)容易陷入局部极小值而导致违反约束。2)只适合处理简单指向约束的情况。对于多轴复杂指向约束，采取线性加权组合的方式，具有一定的局限性。3)无法对能量消耗和机动时间等指标进行优化。

2.1.2图搜索方法

图搜索方法以已知信息的姿态和约束空间为基础，通过构建地图搜索寻找到达目标的机动路径，需要首先对姿态空间或者姿态参数空间进行投影离散网格划分，然后采用图搜索算法求解得到满足指向约束的姿态机动路径。相应的图搜索算法常见的采用 A*搜索算法，其最初由Stanford研究院的Hart等[27]发表，通过构造启发式函数，A*算法可以获得较好的寻的性能，其原理图如图6所示。

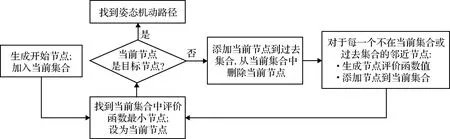
图6 以A*算法为例的图搜索算法原理图Fig.6 Diagram of graph search algorithm using A* as an example

图搜索方法能够有效地处理多轴复杂指向约束，但是只适用于几何类型约束，且无法处理角速度和控制力矩有界约束以及姿态动力学约束。对于内部姿态约束只能在姿态跟踪控制算法中考虑。

2.1.3随机规划方法

空间离散化随机规划方法首先是在机器人运动规划领域得到了大量的应用。Kavraki等[11]首先提出了概率路线图法，这是一种静态空间中的运动规划方法。LaValle团队[12,28-29]在此基础上提出了快速搜索随机树(Rapidly-exploring random tree, RRT)方法，其原理流程图如图7所示。针对复杂指向约束下的姿态机动问题，Frazzoli团队[30-31]利用基于概率路线图和RRT的混合方法作为全局规划器进行姿态扩展，并且基于李雅普诺夫函数建立局部制导律，最终得到安全可行的姿态机动路径。仲维国等[32]采用罗德里格斯参数的姿态描述方式，将指向约束表示成罗德里格斯参数空间中的单页双曲面，并且证明了姿态的直接欧拉旋转对应着该空间内两姿态点的直线连接，同时结合RRT算法规划出安全可行的姿态路径。但是他们都未考虑控制输入受限和角速度受限问题，即有界约束。Cheng等[33]以RRT为框架规划满足指向约束的全局路径，通过滑模控制生成满足有界约束和动力学约束的局部扩展节点，从而得到从初始状态到目标状态的可行路径。Xu等[34]同样将RRT作为全局规划器，而在局部扩展时将运动学、动力学和有界约束转化为线性约束后用二次规划方法求解，并且对新生成的节点进行障碍检测确保满足指向约束。

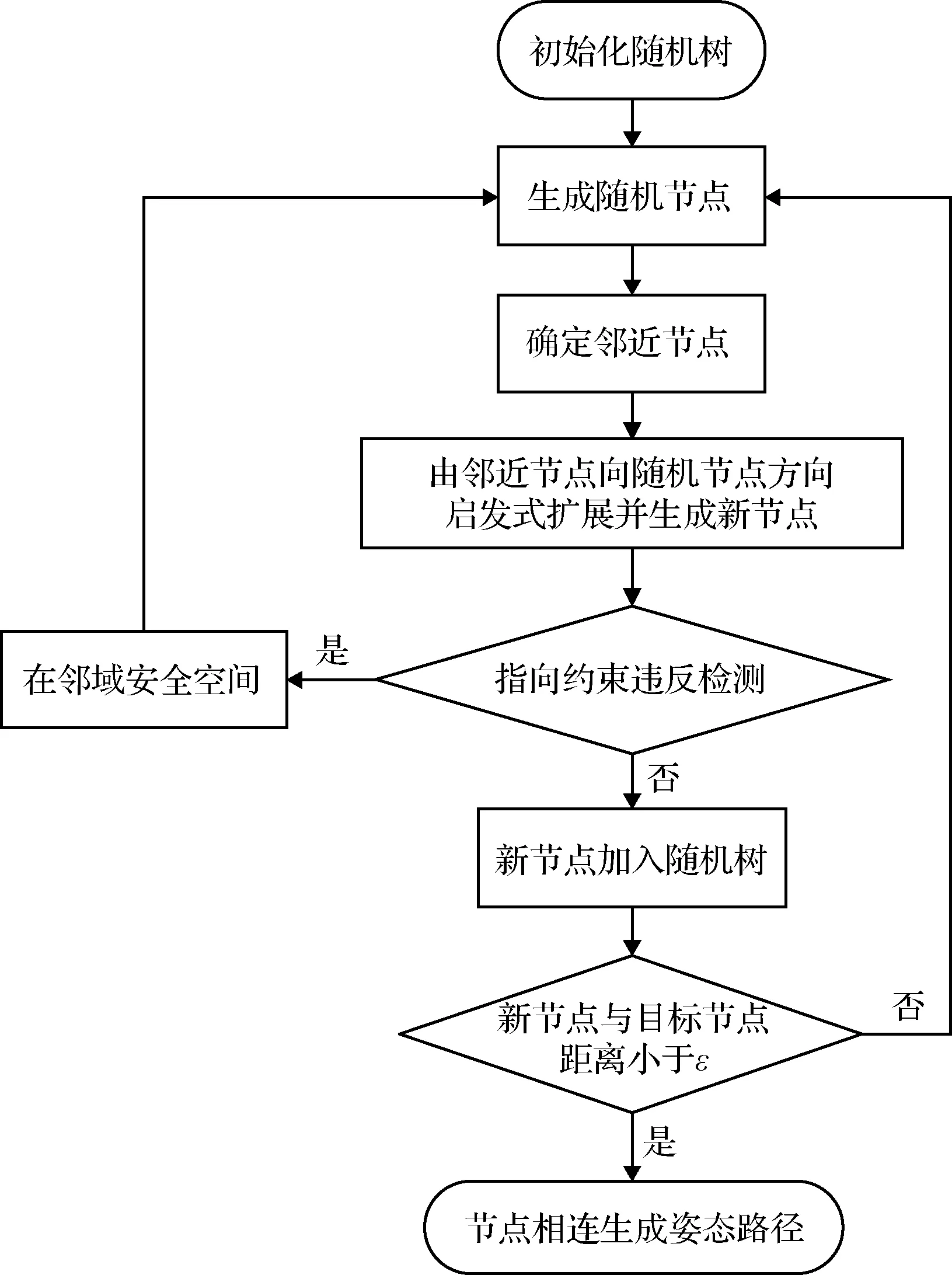
图7 RRT方法原理流程图Fig.7 Flow diagram of RRT method

随机规划方法能高效适应航天器的各种复杂约束情况，但其随机扩展过程生成的路径具有不确定性，而且姿态机动路径容易产生退绕问题。

2.1.4元启发式方法

特别地，当处理姿态路径的优化问题时，以特定自然现象的模拟为搜索模型，即高层次的通用型启发式，称为元启发式方法。元启发式方法广泛应用于姿态机动、姿态确定和轨迹规划等领域，可以适用于能量消耗或者机动时间等不同优化目标，在姿态空间的状态节点扩展中兼顾了局部搜索和随机生成的平衡性。

如图8所示，基于个体的元启发式方法以各种模拟搜索算法为主，基于群体的元启发式方法主要包括不同的群智能算法。Melton[13]检验了粒子群优化、差分进化和细菌觅食等方法，然后将这些方法得到的解用作伪谱法的初值猜测。随后，Melton[35]又检验了自适应协方差矩阵进化策略算法，评价了该算法单独处理无指向约束下时间最优姿态机动问题以及作为伪谱法的初值猜测来解决单轴禁忌约束下时间最优姿态机动问题的性能。缪远明等[36]以快速最优为目标，基于比例微分控制设计编码方法并用于评价函数，而后采用粒子群优化算法求解单轴禁忌约束下的快速姿态机动路径。Spiller等[37]将粒子群优化算法应用于姿态运动学过程，并且结合逆动力学方法求解控制力矩。Pontani等[38]针对无指向约束和单轴禁忌约束这两种时间最优姿态机动问题分别研究了多种元启发式方法，包括逆动力学下的粒子群优化和烟花算法以及自适应协方差矩阵进化策略算法和间接元启发式算法。Wu等[39]通过优化算法计算中间节点，间接实现姿态规划的全局时间最优，最后采用差分进化算法实现约束满足和路径求解。Spiller等[40]又进一步地将逆动力学粒子群优化算法应用于求解飞轮控制下的单轴禁忌约束时间最优姿态机动问题。Wu等[41]在近似能量最优姿态机动规划问题中对差分进化算法进行了改进并求解。

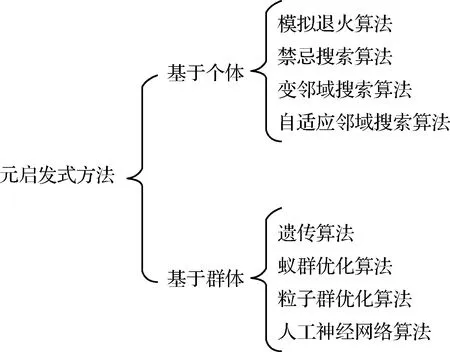
图8 元启发式方法的分类Fig.8 Categorization of metaheuristic algorithms

元启发式方法具有姿态机动路径的能量或时间优化问题求解能力，但是现有的算法主要针对单轴禁忌约束的情况，而且目前的元启发式方法计算效率不高。

2.2 约束简化松弛方法

约束简化松弛方法将航天器姿态规划问题转化为非线性规划问题(Nonlinear programming, NLP)，将复杂多约束进行适当简化松弛变形，求得满足约束的非线性解。约束简化松弛方法总的来说计算资源要求低，有较好的在轨适用性。约束简化松弛方法从传统非线性规划方法发展而来，传统非线性规划方法解决了二次规划、半正定规划和非凸姿态指向约束的凸化等问题，进一步引入松弛思想，增强了复杂指向约束下能量最优问题的求解能力。伪谱法将最优控制问题转化为离散的非线性规划问题，将最优解曲线参数化简化，实现对姿态规划的能量最优和时间最优问题的求解。

2.2.1传统非线性规划方法

传统非线性规划方法以非凸二次规划问题为对象，进行一定程度的简化。序列二次规划(Seque-ntial quadratic programming, SQP)和半正定规划是其中较为基础和典型的两种方法。

对于姿态机动的非线性规划问题，序列二次规划算法在每次迭代中对目标函数泰勒展开至二阶，然后求解二次规划子问题。其优点是易收敛、计算资源要求低，缺点在于对于复杂规划问题的计算量很大。

半正定规划是线性规划的一种推广，又是非线性规划问题的简化，半正定规划与非线性规划的关系见图9。半正定规划求解线性函数极大极小值问题，它同时是一个非光滑的凸优化问题。其优点是在满足严格松弛条件时能够获得全局最优解，缺点在于对于不满足松弛条件的系统只能获得全局最优解的一个不可行的下界, 求解中等以上规模系统时计算时间过长。

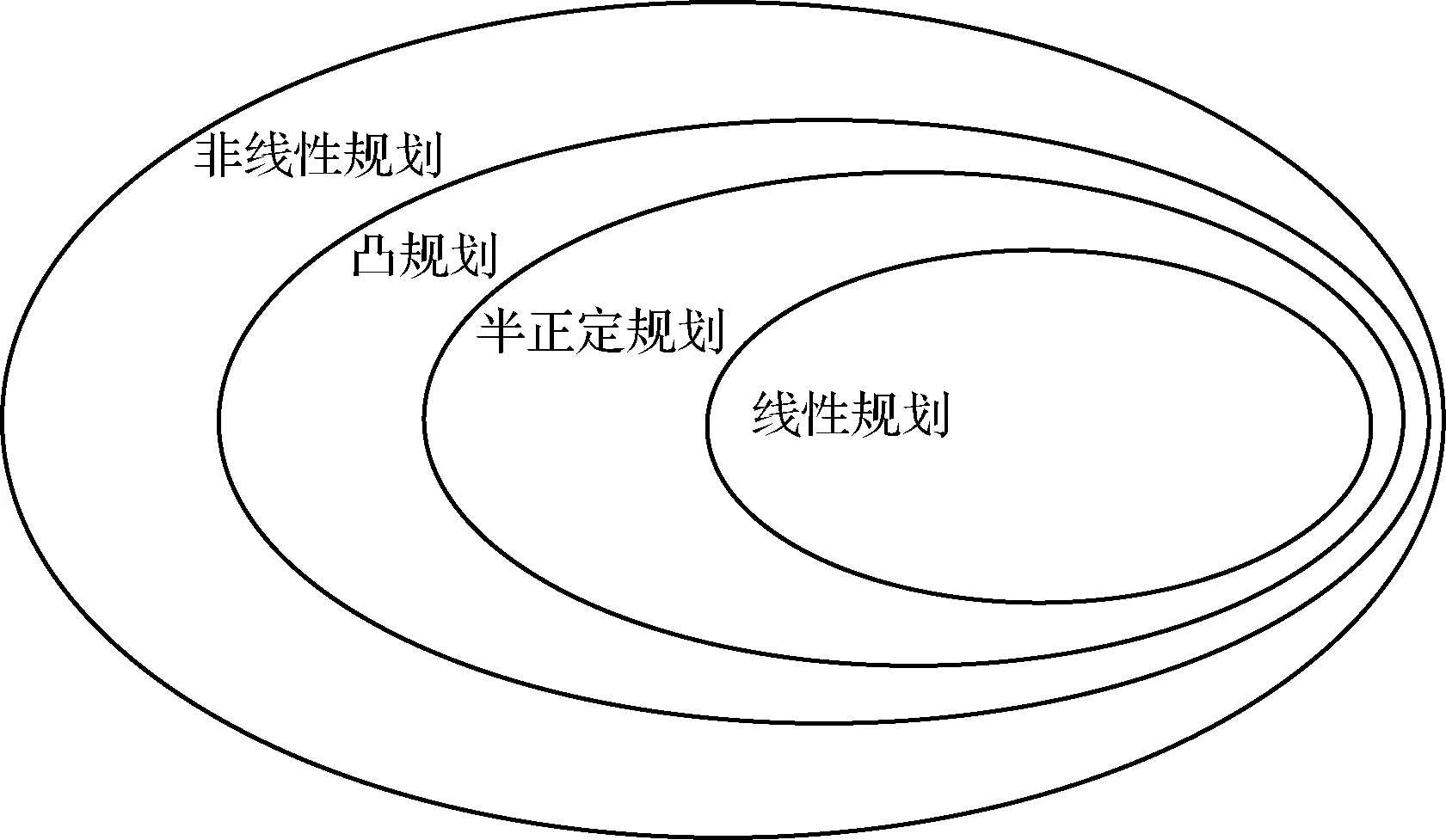
图9 非线性规划和半正定规划的关系Fig.9 Relationship of nonlinear programming and semi-definite programming

传统非线性规划方法需要解决非凸姿态指向约束的凸化问题，以半正定规划为例，Kim团队[42-43]采用姿态四元数的描述方式，将边界条件表示成二次目标函数，将姿态指向约束转化成凸化二次型，转化为半正定规划问题求解得到姿态机动路径。但是该算法采用的单步规划模式在有界约束的限制下容易造成违反指向约束的情况，而且无法对机动时间等指标进行优化。在此基础上，程小军等[44]证明了姿态机动过程中禁忌约束满足非凸二次约束。构造正定海塞矩阵实现约束凸化。最后采用预测控制方法克服了姿态机动路径求解的收敛性和指向约束规避问题。Walsh等[4]将Kim的工作扩展到由旋转矩阵构成的矩阵李群SO(3)上，同样采用半正定规划方法生成姿态机动路径解。

传统非线性规划方法引入松弛思想，通过松弛方法标定非线性规划问题的最优值范围，主要用于求解能量最优问题。Sun和Dai[8,45]将原问题半定松弛为半定规划问题，迭代得到能量最优解。武长青等[5]将原非凸二次规划问题线性松弛，求出低能量的近优解。这些方法可以得到低能量的姿态机动路径，但是计算效率较低。

传统非线性规划方法对原有的航天器姿态机动的非线性规划问题进行简化，但是在路径节点或者约束数量较多的时候非线性规划工具的求解效率和求解能力就会显著下降。

2.2.2伪谱法

伪谱法是一种求解最优控制问题的直接法，也是一种非线性规划方法，既能求解能量最优问题，又能求解时间最优问题。伪谱法采用正交配置法设计基函数，利用正交多项式对状态和控制变量进行插值近似，实现微分代数方程的简化配置，对最优控制问题利用现有的非线性规划算法进行求解。伪谱法在正交多项式(如拉格朗日多项式)上通过配点法插值近似最优解曲线，如式(11)：

(11)

式中：任意函数u(x)的谱表示为其在≤N次多项式ψn(x)空间上的正交投影。

根据所采用的插值配点的不同也衍生出不同的伪谱法(如图10)，传统上比较有代表性的是勒让德伪谱法、高斯伪谱法和切比雪夫伪谱法，如勒让德伪谱法选择勒让德(Legendre)多项式的根为配点。新的伪谱法经过Brikhoff变型，包括勒让德-高斯法、勒让德-高斯-罗贝托法、切比雪夫-高斯-罗贝托法[46]。国际空间站通过跟踪由勒让德伪谱法产生的姿态机动路径先后完成了数次大角度姿态机动[14]。蔡伟伟等[47]为了消除微分方程约束和降低设计空间维数，运用微分平坦理论建立原问题到平坦输出空间的映射，给出了参数化平坦输出的切比雪夫伪谱法，最终转换为非线性规划问题求解。易中贵等[48]利用勒让德伪谱法离线规划得到仅带有两组喷气推力器的非轴对称欠驱动航天器的最短时间姿态机动参考轨迹。

图10 伪谱法按原理分类Fig.10 Categorization of pseudospectral methods

伪谱法通过构造节点求姿态规划问题的离散优化解，节点处满足约束而未对离散节点间的连续路径进行约束检测。如果增加离散节点个数，则会降低伪谱法的计算效率。

2.3 约束几何规避方法

约束几何规避方法通过几何方法设计路径规避复杂指向约束。该方法将以禁忌约束为代表的指向约束标示为禁入区域，采用路径约束检测消除无效约束。通过建立映射关系，在二维平面上处理三维指向约束，使用球面几何距离计算推导中间路径节点并生成约束规避路径。得到姿态机动路径的规划指令集后，由控制器执行跟踪控制。

约束几何规避方法根据姿态指向矢量、约束方位矢量等计算球面几何距离从而设计姿态机动可行路径。Frakes等[15]设计了一个速度避障算法来保护大型重离子望远镜仪器视线轴远离航天器轨道附近的空间危险碎片。该算法保持了望远镜视线轴与航天器速度矢量的夹角不小于90°。Hablani[49]在天球面上基于明亮天体建立排斥域，在姿态机动过程中设计切线路径并得到机动转角和排斥夹角，从而实现指向约束规避。较为典型的约束几何规避方法包括节点分解置换方法和路径转移方法，前者是Xu等[50]提出的基于多节点分解置换的递归规划方法，该方法采用先规划出路径后进行约束违背路径分解置换及重校验的方式，处理了指向和有界约束；后者是Wang等[51]提出的基于路径转移策略的快速规划方法，该方法建立安全路径映射模型简化姿态约束，递进式生成姿态参考路径、松弛路径和指向路径，有效处理多约束问题的同时进一步提高了规划效率。

2.3.1节点分解置换方法

如图11所示，节点分解置换方法当初始姿态路径陷入约束区域时，在约束区域附近设计旋转路径规避约束，递归分解得到新的安全的姿态机动路径，但是需要多次约束检查来判断姿态机动路径是否满足姿态指向约束和有界约束。虽然算法速度优于传统的规划算法，但仍存在一定的时间资源浪费。

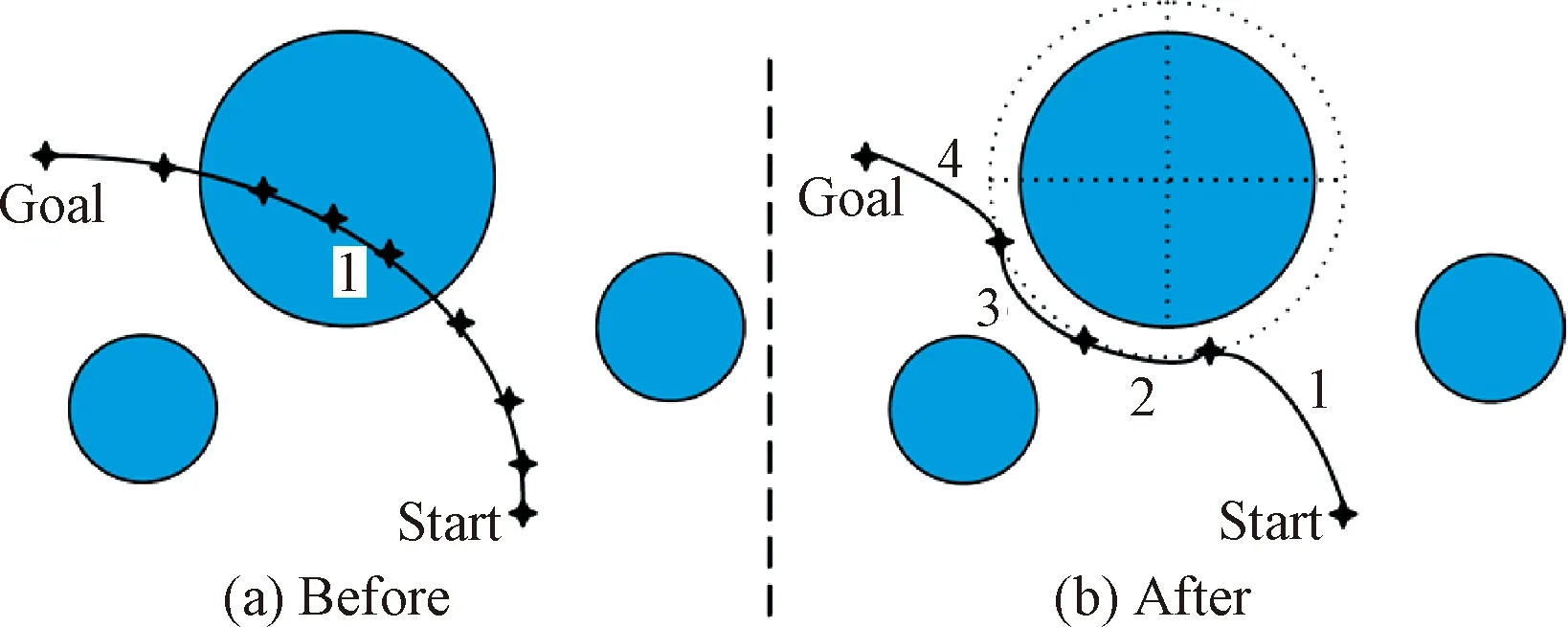
图11 节点分解置换方法的指向约束处理示意图[50]Fig.11 Diagram of pointing constraint processing in multi-node decomposition-and-substitution method[50]

2.3.2路径转移方法

如图12所示，路径转移方法在进行参考路径规划之后，通过松弛路径规划和递进式路径转移规划实现了初始参考路径生成、有界约束满足和指向约束的路径搜索规避，具有一定的时间优化效果。

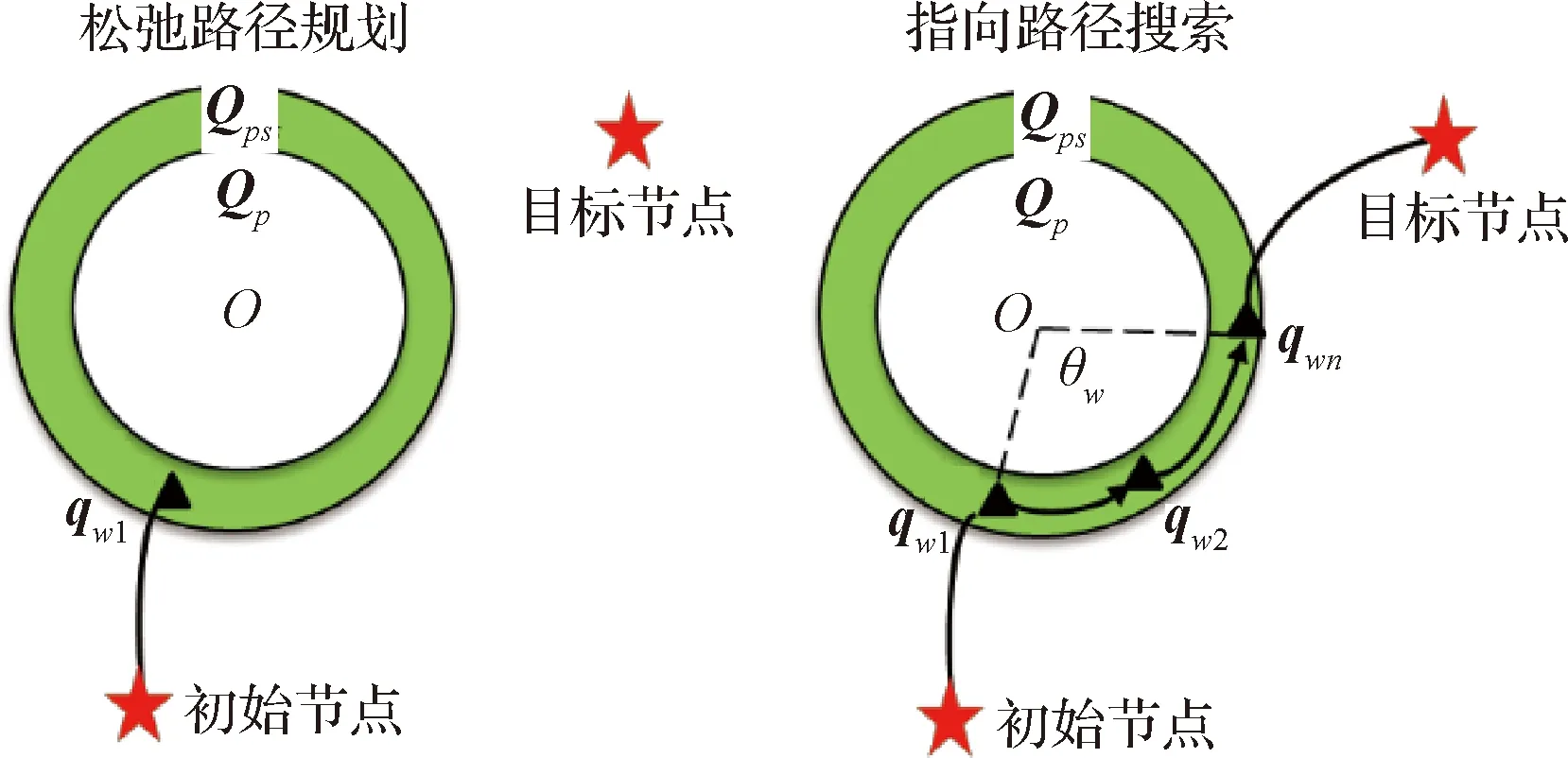
图12 路径转移方法的指向约束处理示意图[51]Fig.12 Diagram of pointing constraint processing in path transfer method[51]

对约束几何规避方法的研究近年来集中于对复杂约束规避策略的设计，同时将该方法用于求解优化问题。约束几何规避方法的优点是能够满足复杂约束并灵活处理优化问题，解决约束规避问题同时节省姿态机动时间。由于是确定性算法，没有随机因素，约束几何规避方法简单直观、计算效率高。但缺点是对于多轴多约束的情况，需要设计合适的规避策略。

2.4 约束解析满足方法

约束解析满足方法采用连续解析的参数化姿态路径表达式，通过优化表达式系数实现约束满足。由于离散形式的姿态机动结果能够满足一般的航天器姿态任务需求，目前关于约束解析满足方法的研究相对较少。当姿态机动的连续解析路径采用多项式表示时，采用多项式方法；近年来微分几何方法也逐步应用于姿态规划问题。

2.4.1多项式方法

多项式方法[16,52-54]通常采用一定阶数的多项式来表示航天器姿态机动过程中的姿态机动曲线(如图13)，然后结合逆动力学方法求解角速度和控制力矩。通过优化多项式系数，实现匹配边界条件和满足指向约束等多种功能。Caubet等[55]利用直接归一化的多项式表示姿态四元数变化曲线，通过迭代自由系数规避简单指向约束。然后利用逆动力学方法和寻根法求解得到满足有界约束的控制力矩和机动时间。最后运用比例-微分四元数反馈控制器跟踪规划得到姿态四元数和角速度曲线，并将规划得到的控制力矩曲线引入前馈控制。

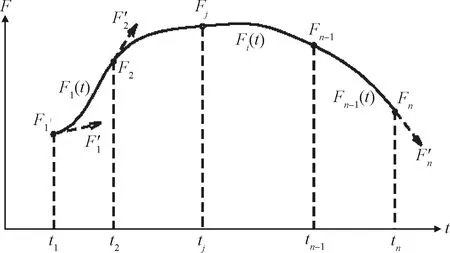
图13 多项式方法的姿态机动曲线[16]Fig.13 Attitude maneuver curve of polynomial methods[16]

多项式方法求解效率高，求解结果连续，但是对指向约束的处理能力较弱。

2.4.2微分几何方法

微分几何方法近几年被应用于求解多约束姿态机动规划问题。该类方法通常基于几何控制理论和极小值原理等理论方法推导一定条件下的姿态机动解析解，而后通过对时间参数或其他虚拟参数的优化实现指向约束和有界约束等约束满足。

Maclean等[56]利用刚体的自然运动来规划小型航天器的姿态机动。该方法通过利用角速度解析解和拉克斯对积分，推导得到航天器姿态在四元数形式下的解析表达式，并通过对解析表达式中自由参数的优化来实现对边界条件和简单指向约束的满足。所求解的参考运动可以被简单的比例微分控制器跟踪控制。Biggs等[57]采用的微分几何方法基于一种旋转矩阵的半解析形式，能够实现指向约束和有界约束处理。该方法在迭代中赋予代价函数不同权值使姿态路径能够规避指向约束，同时路径机动角速度随时间参数化改变，并通过虚拟域和逆动力学的方式来确保满足控制力矩和角速度有界约束。

微分几何方法计算代价较小，解析解的表达方式易于应用，求解结果连续，但是只适合处理简单的小范围姿态指向约束。

3 航天器姿态规划技术发展趋势

随着任务需求的不断变化，姿态规划技术的发展需要适应于航天器在形态结构、控制系统、飞行模式、执行机构等方面的发展。面对新一代航天任务中姿态机动任务的约束条件复杂且较多、对不确定干扰敏感、实时性要求较高的特点，需要从姿态机动的可行解生成、姿态路径优化等方面建立新形式的姿态动力学及规划与优化模型，满足航天器姿态机动规划需求。姿态规划技术发展趋势如下：

1)由单一航天器向多航天器协同发展

在多航天器协同飞行任务中，航天器之间存在姿态机动的协同问题，且可能存在姿轨耦合。因此，提出了多航天器协同姿态规划技术的应用需求，需要建立多航天器协同的相对动力学模型，姿态机动路径既兼顾飞行参考轨迹，又满足姿态机动约束。

2)考虑挠性部件的航天器姿态机动规划

未来航天器向大型化、柔性化发展，挠性附件的存在对姿态机动路径提出了减振需求，基于刚性模型的姿态规划方法难以符合工程需要。针对柔性航天器，重点研究新的姿态动力学模型以及柔性机动路径的平滑处理方法，使姿态规划结果适应于姿态机动控制需求。

3)考虑含可动部件的多自由度姿态规划

航天器在任务中往往安装多个含自由度的敏感器对其他航天器进行跟踪，其中本体与可动部件在姿态上相耦合，需要考虑本体姿态机动和可动部件姿态机动相耦合的动力学模型，通过设计有效的航天器姿态规划方法使本体尽可能少的转动，从而以可动部件的转动代替减少航天器姿态机动的燃料消耗。

4)由单执行机构向多执行机构组合姿态机动规划发展

传统力矩执行机构在提供高精度大力矩时能量效率较低；与之相比，控制力矩陀螺具有能量效率高、不产生污染等特点，但受奇异问题影响较大。同时，单执行机构异常可能导致航天器姿态控制受限。随着航天器单执行机构向多执行机构组合的发展，姿态机动规划问题的控制力矩约束也将更加复杂化、非线性化。

4 结束语

随着姿态机动规划技术的深入发展，对地观测、交会对接、地外天体探测等航天任务广泛应用了相关技术解决姿态机动任务中的规划问题。根据姿态规划的约束处理方法，本文将目前研究中较为成熟的航天器姿态机动规划技术划分为约束评价规避、约束简化松弛、约束几何规避、约束解析满足四种方法类别，梳理了方法的发展脉络，分析、比较并总结了每种方法的优缺点和应用现状。最后基于新一代航天器姿态机动任务的需求，指出了姿态机动规划技术协同化、柔性化、含可动部件、多执行机构组合的发展趋势，需要提出新的姿态动力学和规划模型，在约束处理中考虑耦合、时变的复杂多约束条件，推动姿态机动规划技术在空间科学和工程领域的应用与突破。