主观预期寿命、保险产品定价与对冲效应——基于CHARLS数据的分析

邓睿涵 中南财经政法大学金融学院

张崇林 中国人民保险集团股份有限公司

胡 祥 中南财经政法大学金融学院

一、引言

随着人均预期寿命的稳步提高和人口出生率的逐渐下降，我国人口老龄化进程持续加速。截至2021年，我国65岁及以上人口已突破2亿人，占总人口14.2%，人口老龄化问题日益突出。人均预期寿命持续增长是我国人口老龄化进程加速的重要原因之一。国家卫健委发布的《2021 年我国卫生健康事业发展统计公报》显示，我国居民的人均预期寿命已达到78.2岁，并且这种增长趋势将持续下去。可见，个体与社会在享受长寿所带来益处的同时，也将面临养老资源不足、养老保障不全面等风险（段白鸽，2017）。

人均预期寿命趋势性增加，使得未来平均寿命高于预期寿命所带来的风险，即为长寿风险（胡仕强，2013）。长寿风险给保险行业带来了全新挑战。在保费不变的前提下，预期寿命的提高导致年金产品的给付时间延长，原有的资产负债平衡被打破，保险公司面临收不抵支的超负荷给付风险甚至会陷入财务危机。有关长寿风险的管理问题，国内外学者围绕寿险产品与年金产品的自然对冲效应进行了深入探讨。随后，学者们开始关注通过构建自然对冲模型对长寿风险进行管控的研究。例如：Wang等（2010）结合Lee-Carter模型对未来死亡率变化进行建模，得出了最佳保险产品组合比率；金博轶（2013）、魏华林和宋平凡（2014）基于我国养老金组织机构面临的长寿风险构建自然对冲模型，从而计算保险产品组合的最优比例；曾燕等（2015）构建引入外生产品价格的自然对冲模型，探究保险产品组合的最优配比以降低长寿风险。

未来死亡率的估计偏差是长寿风险的重要来源之一。对保险公司而言，未来死亡率的波动可能会导致寿险产品与年金产品面临定价错配的风险（祝伟、陈秉正，2012）。现有研究中，有关未来死亡率预测的主要依据是反映总体状况的实际死亡率数据。然而，对自身剩余寿命的主观预期也是预测未来死亡率的重要依据之一（段白鸽、陆婧文，2015）。与客观预期寿命依据实际死亡率进行测算的方式不同，主观预期寿命是个体预计自身存活到目标年龄的主观期望，是个体对未来生存可能性的心理预期，可以有效地反映个体未来死亡率（邹小秡、杨芊芊，2019）。自Hamermesh（1985）提出在生命周期建模中应考虑个体的主观预期因素后，学术界对主观预期寿命在未来死亡率预测方面的探讨逐渐深入。Gan 等（2007）与Hurd（2009）利用主观预期寿命拟合出个人主观生存曲线，探究主观生存概率与实际死亡率的关系；Delavande 和Kohler（2009）对比主观预期死亡率与实际死亡率的相关数据，发现主观预期死亡率与实际死亡率在现实生活中变化一致，利用主观预期死亡率计算出的生命周期模型可以更精准地预估人均寿命。

由于主观预期寿命这一因素在未来死亡率的预测中发挥着重要的补充作用，部分学者开始考虑在生命周期模型中引入主观预期寿命这一因素，以弥补实际死亡率在预测过程中缺乏个体主观信息的情形。Wu等（2015）通过引入主观比例因子对实际生存概率模型进行调整，进而分析不同年龄段的老年人年金精算现值的变动及其退休阶段消费计划的变化；O'Dea和Sturrock（2020）将主观生存曲线嵌入生命周期模型中，分析微观个体在主观预期寿命条件下对年金产品的购买需求，从而更好地解释“年金谜题”；Chen 等（2021）发现，主观生存率不同于保险公司所使用的生命表中的生存率，这会导致传统年金产品以及联合养老保险产品的价格有较大差异；王记文（2021）对比了实际死亡率与主观预期死亡率的差异，并利用主观预期寿命进一步分析个体的经济行为。

综上所述，已有的寿险产品和年金产品价格的对冲效应研究主要是在动态死亡率和利率变化的条件下对不同险种组合的自然对冲效应进行分析，尚未有学者在主观预期寿命条件下探讨长寿风险的量化管理问题。目前，我国寿险公司在实务中使用《中国人身保险业经验生命表（2010—2013）》中的静态死亡率数据对保险产品进行定价，难以量化死亡率随时间推移的变动情况，因而无法对未来的死亡率做出准确的预测。相比之下，《中国人口和就业统计年鉴》涵盖了各个年份的死亡率数据，有效地弥补了生命表时效性不足的问题，并且中国健康与养老追踪调查（CHARLS）中的主观预期寿命数据补充了实际死亡率缺乏的个体主观信息，从而为保险公司合理预测未来死亡率，进而有效防范长寿风险提供一种新的视角。

鉴于此，本文考虑在主观预期寿命条件下，基于性别、年龄、保险期限等多个角度，讨论个体在不同年份主观预期寿命的变动情况，进一步分析引入主观预期寿命的终身型、定期型和延期型寿险产品和年金产品的价格变动情况，并利用寿险产品和年金产品价格的反向变动关系进行对冲，探究主观预期寿命条件下不同保险产品组合对冲效应的动态演变规律，以便保险公司更好地管理主观预期寿命所带来的不确定性风险。同时，本文结合当前利率下行这一背景，分析主观预期寿命条件下利率因素对对冲效应的影响，全面诠释保险公司面临的长寿风险。

二、研究设计

（一）引入主观预期寿命的寿险产品和年金产品的精算现值理论模型

1.终身型寿险产品和年金产品

本文分析主观预期寿命条件下，投保年龄为x岁、单位保额的期初付终身年金和期末付终身寿险，其精算现值分别为：

其中，v=1/(1+i)且d=i/(1+i)；kpx为年龄x岁的个体活过k年的主观生存概率；qx+k为x+k岁的个体一年内的主观死亡概率。为计算方便，本文假定寿险产品和年金产品在定价时使用相同的死亡率。

为了进一步研究主观预期寿命条件下的个体生存概率，本文借鉴了Wu（2015）的研究方法，通过引入主观比例因子对实际生存概率进行调整，进而得出个体在主观条件下的主观生存概率。主观比例因子可以理解为个体预期的主观权重，根据公式（1）可知，主观比例因子越高，相应的主观生存概率越低。设τpx为年龄x岁的个体活过τ年的主观生存概率，其计算公式为：

其中，qx+s为x+s岁的个体一年内的死亡概率；c(x)为主观比例因子。

2.定期型寿险产品和年金产品

本文分析主观预期寿命条件下，投保年龄为x岁、单位保额的n年期期初付定期年金和期末付两全保险，其精算现值分别为：

3.延期型寿险产品和年金产品

本文分析主观预期寿命条件下，投保年龄为x岁、单位保额的延期n年的期初付延期年金和期末付延期寿险，其精算现值分别为：

（二）引入主观预期寿命的寿险产品和年金产品对冲弹性理论模型

由于寿险产品和年金产品的价格反向变动存在着天然的对冲关系，本文在主观预期寿命条件下，借鉴段白鸽（2019）关于寿险产品和年金产品对冲效应变化规律的研究，构建对冲弹性模型分析死亡率变化导致的终身型、定期型以及延期型寿险产品与年金产品价格变化的对冲效应。本文假定t0为初始年份，探究由于死亡率变化导致的保险产品价格从初始年份t0到目标年份t的变动情况。

1.终身型保险产品组合的对冲弹性

设e(1)x为x岁的参保者在主观预期寿命条件下，死亡率在[t0,t]时间段内变化导致的终身寿险与终身年金价格的对冲弹性，具体公式如下：

2.定期型保险产品组合的对冲弹性

设e(2)x为x岁的参保者在主观预期寿命条件下，死亡率在[t0,t]时间段内变化导致的两全保险与定期年金价格的对冲弹性，具体公式如下：

3.延期型保险产品组合的对冲弹性

设e(3)x为x岁的参保者在主观预期寿命条件下，死亡率在[t0,t]时间段内变化导致的延期寿险与延期年金价格的对冲弹性，具体公式如下：

由于寿险产品与年金产品的价格整体上呈反方向变动，年金产品价格的上涨可以被寿险产品价格的下降所抵消，从而可以有效避免长寿风险所带来的影响。因此，本文考虑利用对冲弹性模型量化在保单有效期内寿险产品价格与年金产品价格的变化情况。当对冲弹性为负时，表明寿险产品与年金产品的价格呈反方向变动，二者存在对冲效应，并且绝对值越大说明对冲效果越好。

（三）对冲效应的利率弹性模型

利率因素对保险产品组合的价格变动有着重要的影响，故本文在主观预期寿命条件下，通过引入利率弹性模型以探究不同利率水平下保险公司面临的长寿风险。设受对冲弹性影响的利率弹性为Δr，具体公式如下：

三、实证分析

（一）数据来源及其说明

本文使用的数据来源于中国健康与养老追踪调查（CHARLS）和《中国人口和就业统计年鉴》。

主观预期寿命的数据来源于2015 年和2018 年CHARLS 数据库。由于数据库中95 岁以上人口占比较小，难以反映该年龄段的整体特征，因此，本文选择研究年龄为45—95岁的受访者。在剔除变量的缺失值后，2015年和2018年样本量分别为16272人和15910人。中心死亡率数据来自2015年和2018年《中国人口和就业统计年鉴》。

（二）相关数据计算

1.主观预期寿命

本文使用主观生存概率量化主观预期寿命。CHARLS 数据库以受访者的当前年龄为依据，并在此基础上询问其活到某一目标年龄的主观可能性，如表1所示。本文将回答选项设置为1（几乎不可能）、2（不太可能）、3（有可能）、4（很可能）、5（简直一定）五个等级。

由于本文选择研究的是45—95 岁的受访者，因此本文只关注75岁、80岁、85岁、90岁、95岁、105岁、110岁这七个目标年龄。本文将5个回答选项分别与0、25%、50%、75%、100%的概率相对应，求出不同性别、不同年龄的受访者存活到目标年龄概率的平均值，从而分别计算出2015 年和2018 年45—95 岁受访者的主观生存概率，并将其与2015年和2018年的实际生存概率进行对比。

由图1可知，2018年的受访者实际生存概率和主观生存概率在整体上均高于2015年，并且主观生存概率明显低于实际生存概率，不过在85 岁之后，这种差距随着年龄的增长逐渐缩小。分年龄段来看，2015年和2018年受访者的主观生存概率在65岁之后下降较为明显，但在85 岁之后呈现一定的上升趋势；分性别来看，与女性相比，男性的主观生存概率更高，这与实际生存概率的结果相反。可见，女性比男性更容易低估自己的寿命。

▶表1 受访者当前年龄与目标年龄的对照表

▶图1 主观生存概率与实际生存概率的比较

2.死亡概率

常用的死亡率指标包括中心死亡率mx和死亡概率qx。中心死亡率mx表示年龄为x岁的个体在一年内的死亡人数与总人数的比值；死亡概率qx表示年龄为x岁的个体在一年内死亡的概率，该指标在保险产品定价中发挥着重要的作用。本文利用英国学者伐尔（Farlle）所提出的计算公式来表示中心死亡率mx与死亡概率qx之间的关系：

根据《中国人口和就业统计年鉴》的中心死亡率数据并结合公式（9），可以计算出2015年和2018年男性与女性的死亡概率qx，如图2所示。由于《中国人口和就业统计年鉴》没有高龄死亡概率的相关数据，故本文选择利用多项式拟合的方式补齐缺失值。

由图2 可知，分年龄段来看，男性和女性在不同年份的死亡概率在45—85 岁差距不大，而在85 岁之后，2018 年死亡概率明显低于2015 年；分性别来看，女性的死亡概率低于男性，这与实际情况相一致。

（三）主观预期寿命条件下的对冲效应分析

1.不同险种价格的定量分析

2019年，银保监会发布通知，将普通型人身保险保单评估利率上限定为年复利3.5%和预定利率的较小者。因此，本文选择在3.5%的预定利率条件下，分析保险产品的价格变动。图3至图8分别表示在利率为3.5%的假设下，2015年和2018年不同性别的投保者在主观预期寿命条件下购买的终身年金、终身寿险、20 年期定期年金、20 年期两全保险、延期20年给付的递延年金和延期20年给付的递延寿险的精算现值。为进一步判断主观预期寿命对保险产品价格的影响，本文将其与客观预期寿命条件下的保险产品价格进行对比。

▶图2 2015年和2018年分性别死亡率

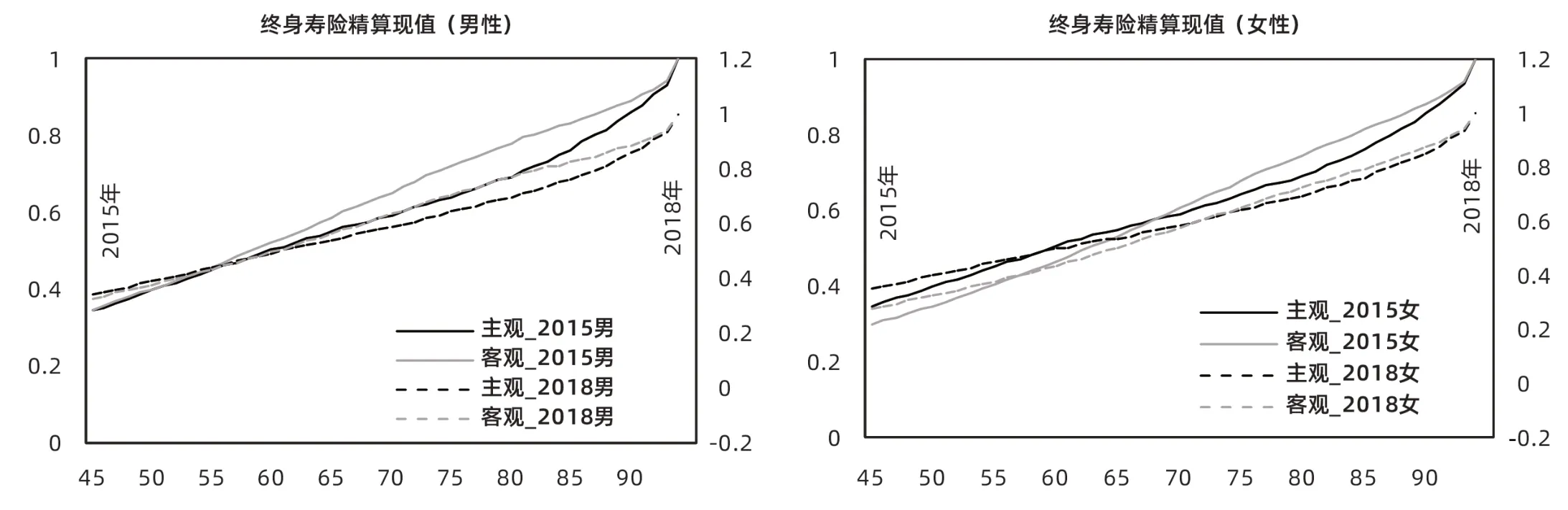
▶图3 主观预期寿命与客观预期寿命条件下终身寿险精算现值

由图3 至图8 可知：第一，在主观预期寿命和客观预期寿命条件下，终身寿险和两全保险的精算现值随着年龄的增长逐渐提高，而终身年金、定期年金、递延年金和递延寿险的精算现值则逐渐降低。第二，在主观预期寿命和客观预期寿命两种不同条件下，与2015 年相比，2018 年年金产品的精算现值在整体上提高，而2018 年寿险产品的精算现值在整体上降低，并且主观预期寿命条件下不同年份寿险产品和年金产品价格的变化幅度高于客观预期寿命。值得注意的是，2018 年部分年龄段延期寿险的精算现值高于2015 年，这一反常现象将会导致延期型保险产品组合面临的长寿风险更显著。第三，男性寿险产品和年金产品价格的变化幅度明显高于女性（特别是在主观预期寿命条件下），说明死亡率的变化对于男性的影响更大，男性面临更严峻的长寿风险。

由于年金产品和寿险产品的价格呈反方向变动，在固定利率条件下，寿险产品价格的下降部分能够对冲年金产品价格的上升部分，这在一定程度上可以弱化长寿风险对保险公司经营的影响。那么，与客观预期寿命相比，在主观预期寿命条件下，保险产品的对冲效果如何？主观预期寿命对不同年龄段的对冲效应有着怎样的影响？对冲作用后男性与女性所面临的长寿风险存在着怎样的差异？为解答这些问题，本文引入了对冲弹性，进一步分析在主观预期寿命条件下，保险产品组合对冲效应的动态演变规律。

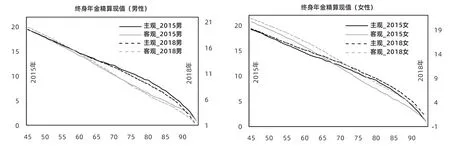
▶图4 主观预期寿命与客观预期寿命条件下终身年金精算现值

▶图5 主观预期寿命与客观预期寿命条件下20年期两全保险精算现值

▶图6 主观预期寿命与客观预期寿命条件下20年期定期年金精算现值

▶图7 主观预期寿命与客观预期寿命条件下延期20年给付的递延寿险精算现值

▶图8 主观预期寿命与客观预期寿命条件下延期20年给付的递延年金精算现值

2.不同保险产品组合对冲效应的动态演变规律

图9 至图11 给出了在3.5%固定利率假设下，45—95 岁男性和女性分别在主观预期寿命与客观预期寿命条件下，于2015—2018 年参保的终身型、定期型和延期型寿险产品和年金产品组合价格的对冲弹性。

由图9至图11可知：第一，整体而言，在主观预期寿命与客观预期寿命两种条件下，终身型和定期型保险产品组合的对冲弹性均为负值，这主要是因为这两个组合中寿险产品和年金产品的价格呈反方向变动；延期型保险产品组合的对冲弹性出现了部分正值，面临的长寿风险更加显著。第二，终身型和定期型保险产品组合的对冲弹性绝对值随着年龄的增加而减小，说明高年龄段人群面临的长寿风险更加严峻；对于延期型保险产品组合，在客观预期寿命条件下，对冲弹性为正值且随着年龄的增加而增大；而在主观预期寿命条件下，对冲弹性于50—65 岁出现部分正值且高于客观预期寿命条件下的对冲弹性，因此，要特别关注延期型保险产品组合中男性与女性面临的长寿风险。第三，在客观预期寿命条件下，女性的对冲弹性绝对值始终高于男性，

这是因为女性的实际死亡率始终低于男性；而在主观预期寿命条件下，由于女性和男性对于预期寿命的主观看法存在差异，不同年龄段的男性和女性的对冲效应不同。在主观预期寿命条件下，对于终身型和定期型保险产品组合而言，当年龄较低时，女性对冲弹性绝对值低于男性，但随着年龄的增长，女性对冲弹性绝对值逐渐超过男性。可以反映出低年龄段男性面临的长寿风险低于女性，而高年龄段男性与女性相比面临的长寿风险更高；对于延期型保险产品组合，低年龄段女性的对冲效果更加显著，而高年龄段女性的对冲效应整体上弱于男性，面临的长寿风险更加严峻。

▶图9 2015—2018年终身寿险与终身年金的对冲弹性

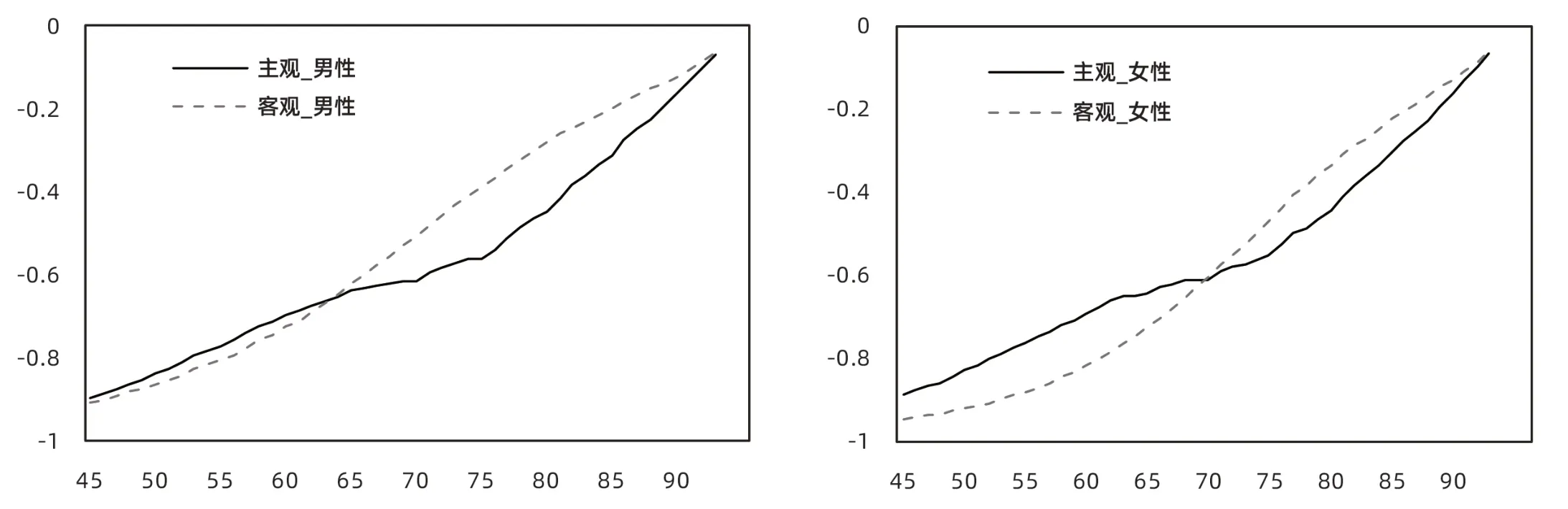
▶图10 2015—2018年两全保险与定期年金的对冲弹性

▶图11 2015—2018年延期寿险与延期年金的对冲弹性

（四）低利率背景下的对冲弹性分析

当前，在全球经济下行的影响下，各国央行实施宽松的货币政策，相继下调利率。我国目前的预定利率相对较高，但在全球经济低利率时代下，受经济增速放缓、利率市场化、人口结构失衡等方面的影响，我国将长期面临利率下行压力。低利率环境下，长寿风险对保险公司经营的影响愈加显著。为进一步探究主观预期寿命条件下利率因素对长寿风险的影响，本文分析了在2015—2018年不同利率水平下，三种保险产品组合对冲弹性的变化情况。具体结果如图12 至图14所示。

从图12至图14可知：随着利率的下降，对冲弹性不断减弱，长寿风险更加显著。分年龄段来看，随着年龄的增长，利率变化对于对冲效应的影响逐渐减弱；分性别来看，利率对于不同性别的对冲效应影响不同，特别是对于延期型保险产品组合来说，在不同利率水平下，男性对冲弹性变化幅度明显高于女性。因此，在利率下行这一大背景下，保险公司将会面临更加严峻的长寿风险。

四、研究结论与建议

本文在主观预期寿命条件下，通过引入对冲弹性模型，从性别、年龄、延期期限等多个角度探讨寿险产品与年金产品组合的自然对冲效应动态演变规律，并且分析利率这一敏感性因素对不同保险产品组合对冲效应的影响。

研究结果表明：第一，整体上，预期寿命的延长使得居民的主观预期寿命提高，然而在部分高年龄段，主观预期寿命并没有相应的提高，并且女性与男性相比更容易低估自己的寿命。第二，在主观预期寿命与客观预期寿命两种条件下，随着年龄的增长，保险产品组合的对冲效应逐渐减弱，面临的长寿风险更加严峻。对于终身型和定期型这两种保险产品组合来说，低年龄段男性的对冲效果更强，而在高年龄段，女性的对冲效果更显著。对于延期型保险产品组合来说，低年龄段女性的对冲效果明显优于男性，高年龄段女性的对冲效果弱于男性。第三，在主观预期寿命条件下，利率的变化对保险公司面临的长寿风险有重大影响。特别是在当前利率下行这一大背景下，随着利率的降低，保险公司的长寿风险更加显著。

针对上述结论，本文提出如下建议：第一，未来死亡率预估的准确性对保险公司合理管控长寿风险起到了重要的作用。因此，保险公司在死亡率预测中可以拓展数据来源，及时更新数据，通过引入个体的主观预期寿命等因素对长寿风险量化模型进行优化。第二，保险公司在进行寿险产品与年金产品开发时，应考虑到在主观预期寿命条件下，不同性别、年龄下寿险产品与年金产品价格存在的差异，科学合理地厘定寿险产品与年金产品的价格和配置比例，从而有效地规避长寿风险。第三，在利率下行这一大背景下，利率的降低会导致保险产品组合的对冲效果下降。因此，保险公司需及时关注利率变化的动向并建立利率风险防范机制，以化解利率风险带来的冲击。

▶图12 不同利率水平下终身型保险产品组合价格的对冲弹性

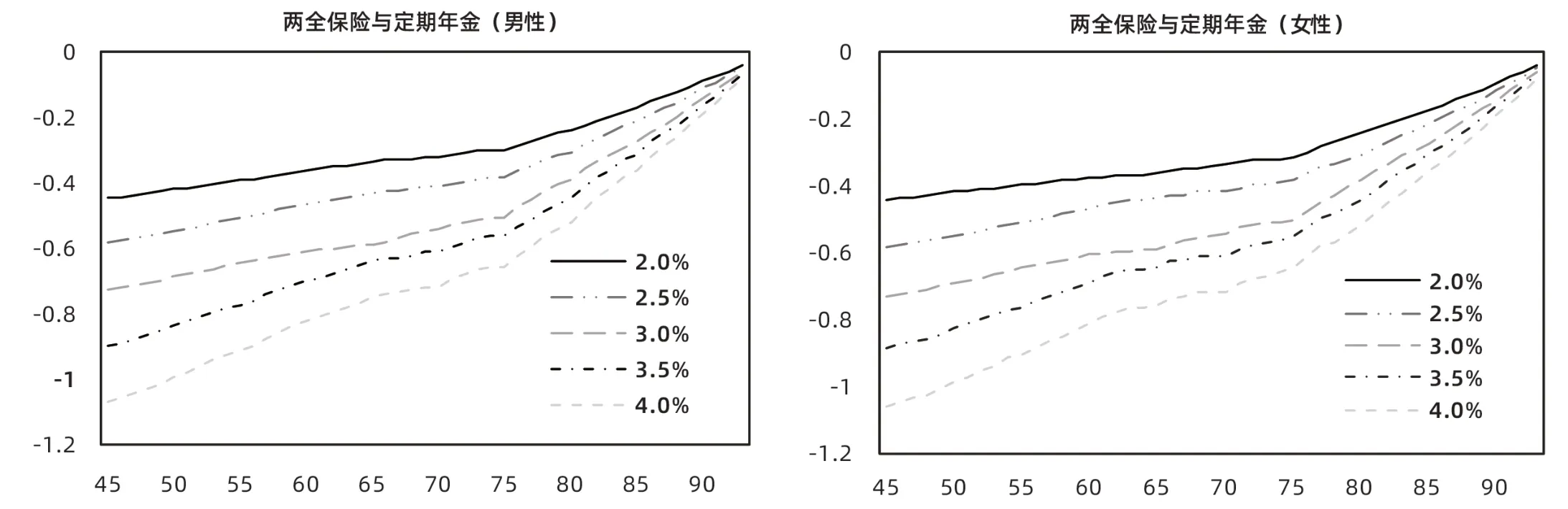
▶图13 不同利率水平下定期型保险产品组合价格的对冲弹性

▶图14 不同利率水平下延期型保险产品组合价格的对冲弹性