思维导图在高中数学教学中的应用

陈妍

【摘要】思维导图是利用图表视觉形象化地表达知识的工具，借助思维导图并结合问题串组织教学，能够让学生有效进行自主探索，实现思维过程的教学，进而帮助学生构建完善的认知结构，积累数学活动经验，最终体会数学的精神.文章从以“旧”探“新”、设计活动、精选例题三个角度出发，并通过三个案例说明思维导图在高中数学教学中的应用策略，最后提出实现思维过程教学、实现“两次倒转”的教学机制、丰富学生基本活动经验的应用策略，以供参考.

【关键词】思维导图；迁移；高中数学；应用

【基金项目】福建省中青年教师教育科研项目（基础教育研究专项）《新课程背景下培育学生深度学习新教材的有效途径研究》；项目编号：JSZJ21067；（福建教育学院资助）

引 言

在高中数学教学中经常遇到学生反馈这样的问题，明明上课都听得懂但做作业时就屡屡碰壁，没有思路.这是因为学生对知识仅停留在浅层的认识上，只知道有这样的一个概念、一条定理，并没有真正理解知识的本质，难以将知识串联起来.数学知识是需要学生经历一系列丰富的教学活动习得的，当遇到问题时则需要借助于过往积累的活动经验解决.

一、思维导图概述

思维导图最初作为一种高效记笔记和提高记忆的学习工具，以放射思维为基础通过绘制导图模拟人脑神经网络结构，导图结构包括中心主题与层级结构，图中关键词类似于神经网络中的神经元，由它可引发出各类关联.思维导图依靠文字、符号、图像链接和传递对应的信息，实现知识点整理及知识间衔接.思维导图引入教学，给学生提供了一个思维可视化的学习环境，用连线展示概念间的关系，描绘了知识与学习发生过程的一种映射.

二、思维导图融入高中数学教学的实践案例

现阶段，在培养学生核心素养的过程中，教育更推崇以教师为主导，以学生为主体的教学模式，在教师的引领下，学生开展有目的的自主学习活动.笔者尝试在教学中引入思维导图，帮助学生积累课堂活动经验：给学生布置预习任务，以“旧”知识为生长点探索“新”知识，绘制思维导图建构知识网络，从而让学生了解整体知识网络；在知识教学环节中，教师借思维导图帮助学生厘清探索路径发现数学本质；在解题教学过程中，教师整理解决问题的方法，同时串联知识间的关系.下面笔者以人教A版必修第二册中，第八章关于“垂直”关系的几个教学环节为例，谈谈借助思维导图，丰富学生课堂学习经验的设计理念.

（一）以“旧”探“新”，帮助学生积累独立认识新知识的经验

案例1 “直线与平面垂直”课堂引入的情境创设

课前任务：预习课本“空间直线与平面垂直”内容，完成本节思维导图.

课堂引入问题：类比之前直线与平面平行的知识的学习过程，关于直线与平面的垂直，需要研究哪几方面的内容？

提问：研究方法是什么？

评注：学生通过预习生成的导图，导图里除了串联着本章的知识，还有一些思维形成的过程，学生可以根据自己的情况将它补充完整.以“单元—课时”知识整体性思想让学生阅读“空间直线与平面垂直”整节内容，完成思维导图.通过绘制思维导图培养学生养成预习阅读课本的习惯，也给学生积累了独立认识新知识的经验，然后带着对新知识一些初浅的印象和问题进入课堂.通过思维导图的铺垫，唤醒学生之前关于“平行”内容的学习经验，借助经验继续探索新知识.

（二）设计活动，帮助学生积累抽象问题本质的经验

案例2 “直线与平面垂直”定义的生成

图2为笔者关于概念生成这一教学环节绘制的“点的思维”导图，“点的思维”指的是学生对某个特定知识点进行探索而产生的思维，这里即是对概念学习的一种思维.在引导教学的过程中结合问题链展开学习.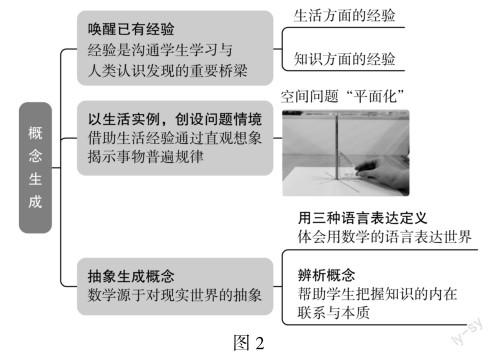

问题：旗杆与地面有怎样的位置关系？

追问1：大家都认为旗杆与地面是垂直的，那如何理解“垂直”呢，大家认识中的垂直是怎样的或者说不垂直是怎样的？

追问2：如何给直线和平面垂直下定义？（启发：在研究直线和平面平行时，我们将空间问题转化为平面问题去分析和处理，在探索直线和平面垂直时，我们同样可以采用类似“平面化”的思想进行研究）.

学生动手实验：将铅笔当作旗杆，白纸为地面，当铅笔矗立在白纸上时，它与纸面上的直线有什么关系？（引导学生在过铅笔与白纸的交点上画直线，并利用三角板测量铅笔与这些交线夹角.通过实验学生都发现铅笔所在的直线与这些交線都是垂直的）.

追问3：如何用符号语言描述直线与平面垂直的定义？

追问4：如果直线l与平面α垂直，l与平面α内的任意一条直线有什么关系？

评注：学生直观感知中的“垂直”和定义的内涵存在一定的距离，通过先前的预习学生认识了定义，但还是无法理解“直线与平面内的任意一条直线都垂直”这一性质.教师以旗杆为例，设计铅笔垂直纸面，类比迁移之前的学习经验，将空间问题转化为平面问题辅助学生分析和处理，让学生通过动手操作，理解“任意直线”的含义.经历从实际生活的空间中抽象出几何定义，培养学生的直观想象核心素养.三种语言的互相转化，让学生体会“用数学的语言表达世界”.

（三）精选例题，帮助学生建立已知与未知转化的经验

案例3 “立体几何”教学的研讨过程

例题 如图3，已知PA⊥平面ABC，平面PAB⊥平面PBC，求证：BC⊥平面PAB.

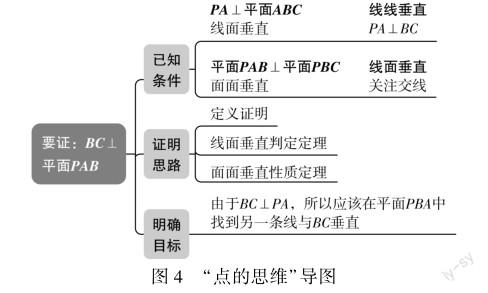
解后提问：例题中涉及线线垂直、线面垂直、面面垂直，大家是否能将这些垂直与前面学的平行关系整理出知识结构图？（学生整理如图5）

这样，通过思维导图罗列题目条件及解决问题的思路，确定最后的目标，使学生解题的思维过程得到显化，加深了学生对解题的印象.数学问题往往需要学生将几个知识点结合起来一起思考，借习题回顾知识，培养学生梳理知识结构图，通过前面定义与判定定理两个“点的思维”的探究学习，引导学生发现知识点间的关系，延伸获得“线的思维”导图，即把知识点由此及彼地联系起来进行思考.

三、思考与启示

（一）實现思维过程教学

数学学科的本质特征，决定了数学具有发展学生理性思维的工具属性.学习是一种从未知的情境出发探索问题解决方案的过程，也是一种复杂思维的互动过程.思维的发生绝不是从死记硬背、机械模仿开始的，它是“反思—问题生成—探究、批判—解决问题”的过程，要想获得好的学习效果，那么免不了有一场深刻的思维活动.

首先，思维过程的教学能够完善学生的认知结构.学习效果与认知结构的完整性是成正比的，简单来说认知结构就是人脑中的知识结构，在皮亚杰的认识论中，认知结构的发展是主客体相互作用的结果.《中国高考评价体系》中也提到了高考需考查学生的综合性，综合性要求学生具有完整的知识网络，且能将不同模块间的知识逻辑连接成整体.本节课笔者尝试借助思维导图帮助学生完善认知结构，课前学生通过预习了解知识整体结构，课上教师从定义讲解再到定理讲解最后到应用，设计由“点的思维”逐渐延伸到“线的思维”，结合问题链的形式引导学生在解决问题的过程中显化思维生成导图，最终将知识再次串联起来.

其次，思维过程的教学能够引导学生进行知识迁移.在一系列思维互动过程中，促使学生通过一次次的研究，感悟更具一般性的思想方法，慢慢学会解决数学问题的相似套路，最终形成数学的思维方式.比如本节课中，引导学生迁移类比直线与平面平行这一“点的思维”的研究套路，经历“直观感知—猜想结论—操作确认”的学习过程.

最后，思维过程的教学能够让学生体会知识背后的数学文化.数学知识源于对现实世界的抽象，揭示事物的本质与规律，它不仅仅有运算推理，还有数学的思想、眼光、语言、精神.比如本节课在抽象定义环节中，虽然学生能够直观地感受到直线与平面垂直的关系，但将直观感知转化为定义还是有很大难度的，因此教师引导学生动手操作、观察世界，培养学生用数学的眼光观察，逐步发现事物的本质，体会了定义生成的纯粹性与完备性.

（二）实现“两次倒转”的教学机制

学生从课本中习得知识的过程，本身就具有高起点性，不需要体验漫长的探索和试错经历，打开课本就能得到前人对一系列现象抽象表达的成果.让学生对知识直接从认识开始，这就是学习的“第一次倒转”，有目的地指向现成成果的学习，通过预习完成教师设计的任务及绘制思维导图，让学生在“第一次倒转”能对知识有初浅的意识，带着这些初浅的意识进入教师主导的课堂，开启教学的“第二次倒转”.为了让“第二次倒转”能真正解决学生从认识开始接触高深知识遇到的困难，就要求教师在教学中要充分考虑学生与知识的心理距离和学习感受，顺应学生思维，让学生能在教师的启发下积极主动地参与学习活动，以知识的发生、发展过程为载体，适时适点地利用问题引发学生思维活动，让课堂教学真正实现思维过程的教学.

（三）丰富学生基本活动经验

数学就是源于对现实世界的抽象，抽象需要借助已有的经验对客观事物的本质进行概括归纳.《普通高中数学课程标准（2017年版2020年修订）》里提到的“四基”中，就有一项是为学生提供必备的数学活动经验，为促使学生自主探索、主动学习提供可能.然而，获得新知识经验主要还是源于课堂，这就要求教师应在充分了解学生知识储备、思维过程、心理情绪等的基础上，通过设计具有明确指向性的课堂活动，调动学生参与的热度.课堂上的学生绝不是一张白纸，教师应注重知识与学生个体经验的相互转化，利用生活中的一些例子与学生过往习得的知识，唤醒学生的经验，让学生自觉融入课堂，使经验成为沟通学生学习与课本知识的桥梁.除了以真实情境融入课堂，教师还可以设计一系列开放的任务和动手操作的活动，让学生合作交流，在不间断的反思、质疑和实践中，利用已经掌握的知识与积累的经验处理各类烦琐、陌生的问题，从而获得解决新问题的经验，提升了直观想象，逻辑推理，数学抽象的核心素养.

结 语

章建岳博士提到过：“只有思维过程的教学才能真正落实学生的‘四基和‘四能.”利用思维导图将数学知识、方法、思想以图形方式串联起来，不仅能辅助学生的记忆，更能将思维外显表达出来.因此，教师应尽力化解教材内容与学生思维、心理的矛盾，优化教学设计，让学生的学习真正发生、深度发生.

【参考文献】

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[2]曹均.利用思维科开展高中数学教学的策略探讨[J].数理天地（高中），2022（23）：67-69.

[3]郭玉峰，史宁中.“数学基本活动经验”研究：内涵与维度划分[J].教育学报.2012（5）：23-28