基于停车视距的强降雨环境下公路车辆制动安全可靠性研究

盛旭高，于梦阁，霍 炜

(青岛大学 机电工程学院，山东 青岛 266071)

0 引言

近年来，我国高速公路里程数已突破14万公里，位居世界第一，但公路行车安全问题仍十分严峻，特别是在强降雨环境下，路面附着系数和能见度较低，驾驶员反应时间较长，致使制动距离变长，事故发生率较晴天相比急剧增大[1-3]。据统计，雨天公路交通事故发生率较晴天高2～3倍，降雨环境驾驶员的行车安全性大大降低[4]。因此，有必要开展雨天行车安全研究工作。

目前，大部分的公路交通事故与停车视距不足有很大关系，国内外学者已在停车视距及其引发的行车安全问题方面开展了大量研究工作。美国国家公路与运输协会标准(Americal Association of State Highway and Transportation Officials，AASHTO)停车视距模型将停车视距简化为匀速行驶阶段和匀减速行驶阶段[5]。德国道路设计规范停车视距模型将驾驶员反应时间分为城内和城外两种，并考虑了空气阻力对停车视距的影响[6]。法国路线设计规范停车视距模型用平均减速度对停车视距进行了描述，平均减速度的取值受路面潮湿状态、轮胎状态、设计速度等因素影响[7]。袁浩等[8]将车辆制动时受到的阻力用制动减速度来表示，并用制动减速度描述了车辆的制动过程。姜虹等[9]针对不良天气高速公路路面附着系数降低和能见度减小的情况，得出一种适用于不同路面条件(干燥、微湿、积水、积雪、结冰)的停车视距计算模型。杨帆等[10]以车辆行驶时的动力学模型为基础，以时间段0.01 s为间隔，对停车视距进行了推导。Bassani等[11]分析了驾驶员在视线受阻环境下的驾驶行为，发现降低车速能有效的减小停车视距，从而保证驾驶员的行车安全。李涛等[12]分析了不同能见度下公路车辆的停车视距，并给出了车辆在不同能见度下的行车安全距离。赵新勇[13]基于AASHTO停车视距模型给出了自由流状态下车辆是否会与前方障碍物发生碰撞的判断方法。

在强降雨环境下，一方面，路面附着系数降低会导致停车视距增大，另一方面降雨又使得驾驶员可视距离变短，从而导致车辆碰撞或追尾的概率增大[14]。目前已有一些学者针对雨天停车视距增大及可视距离变短的问题，开展了雨天公路车辆行车安全的研究工作。Sun等[15]分析了雨天车速及停车视距对行人过路安全的影响，给出了雨天车速应小于45 km/h的建议。孙悦[16]通过停车视距和能见度分析了雨天海绵道路车辆的行车安全性，给出了雨天海绵道路的安全车速建议值。李铁强等[17]选取路面附着系数和能见度为评估指标对雨天道路行车安全性进行了仿真分析，并对雨天行车安全进行了等级划分。

驾驶员在实际制动过程中，由于环境-车辆-驾驶员系统中的许多参数具有随机性，如车速，驾驶员反应时间等，因此，事故是以一定概率发生的，需要采用可靠性的方法对车辆的制动安全进行评估。目前，已有部分学者对车辆的制动安全可靠性工作进行了研究，并有了相关的研究成果。张航等[18]采用一次二阶矩方法讨论了现行规范停车视距设计取值的安全可靠性，用失效概率对停车视距的安全可靠性进行了描述。朱兴琳等[19]用公路供给停车视距值和驾驶员期望停车视距值构建停车视距的功能函数，采用一次二阶矩方法对停车视距的可靠性进行了分析。以上车辆制动安全可靠性的研究工作皆是在晴天环境下进行的，而雨天车辆制动安全可靠性的研究工作尚且较少。

基于此，本研究充分考虑车辆制动过程中坡度阻力的变化情况，对AASHTO停车视距模型进行改进，在此基础上，建立雨天车辆制动安全可靠性模型，基于蒙特卡罗模拟方法计算雨天车辆制动安全可靠性及可靠性灵敏度，对雨天车辆的制动安全性进行评估。

1 停车视距

1.1 制动过程

车辆制动过程中受到的阻力有：滚动阻力、坡度阻力、空气阻力、地面制动力。由于滚动阻力和空气阻力相对较小，因此忽略其对制动过程的影响。制动过程具体如图1所示。分为3个阶段：驾驶员反应阶段、制动器作用阶段、持续制动阶段。

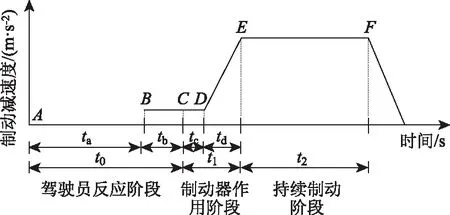
图1 停车视距制动模型Fig.1 Braking model of stopping sight distance

驾驶员反应阶段(AC段)对应时间为t0，即驾驶员接到紧急停车信号到脚接触制动踏板所需的时间，分为思索阶段(AB段)和移脚阶段(BC段)，对应时间分别为ta和tb。在移脚阶段坡度阻力开始产生制动减速度。

制动器作用阶段(CE段)对应时间为t1，即脚接触制动踏板至制动力上升到最大值所需的时间。分为制动间隙消除阶段(CD段)和制动力上升阶段(DE段)，对应时间分别为tc和td。在制动力上升阶段，地面制动力开始产生制动减速度，将其简化为一个线性变化的过程。

持续制动阶段(EF段)对应时间为t2，即车辆以最大制动力持续制动到停车所需的时间。

针对制动过程的3个阶段，建立公路车辆的停车视距模型。

1.2 停车视距推导

在思索阶段(AB段)车辆处于匀速行驶状态，此阶段车辆行驶距离sa为：

sa=v0ta，

(1)

式中v0为车辆制动前的行驶速度。

车辆在移脚阶段(BC段)，任意时刻的车速vb为：

vb=v0-gtsini，

(2)

式中，g为重力加速度；i为纵坡坡度;t为时间。

车辆在移脚阶段(BC段)的行驶距离sb为：

(3)

式中dt为时间t的积分。

驾驶员反应阶段(AC段)的行驶距离s0为：

(4)

车辆在制动间隙消除阶段(CD段)，任意时刻的车速vc为：

vc=v0-gtbsini-gtsini。

(5)

车辆在制动间隙消除阶段(CD段)的行驶距离sc为：

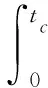
(6)

车辆在制动力上升阶段(DE段)，任意时刻的车速vd为：

(7)

式中φ为路面附着系数。

车辆在制动力上升阶段(DE段)的行驶距离sd为：

(8)

制动器作用阶段(CE段)的行驶距离s1为：

车辆在E点的车速vE为：

(10)

持续制动阶段(EF段)的行驶距离s2为：

(11)

(12)

式中m为车辆质量。

由式(4)，(9)，(12)可得停车视距S为：

(13)

将v0(m/s)化成v(km/h)：

(14)

当路面坡度i较小时，即sini≈i,cosi≈1,式(14)可写为：

(15)

当时间段t1为0,且时间段tb的纵坡坡度为0时，本研究建立的停车视距模型即为AASHTO停车视距模型。

(16)

1.3 停车视距模型对比分析

驾驶员在晴天制动时，驾驶员制动反应时间t0取值为1.2 s[20]，思索时间ta取值为1 s[21],移脚时间tb为驾驶员反应时间与思索时间的差值，即为0.2 s。制动器作用时间t1取值为0.3 s[22]，制动力上升时间td取值为0.2 s[8]，制动间隙消除时间tc为制动器作用时间与制动力上升时间的差值，即为0.1 s。纵坡坡度i取值为2%[23]，晴天路面(干燥路面)附着系数φ取值为0.88[24]，重力加速度g取值为9.8 m/s2。

根据式(15)～(16)计算出不同行驶速度下公路车辆的晴天停车视距值，如表1所示。“AASHTO”表示AASHTO停车视距模型的计算值，“改进AASHTO模型”表示改进AASHTO停车视距模型的计算值。

从表1中可以看出，AASHTO停车视距模型的计算值偏小，原因是AASHTO停车视距模型忽略了移脚阶段和制动器作用阶段制动力的变化情况，改进AASHTO停车视距模型对移脚阶段和制动器作用阶段制动力的变化情况进行了考虑，与实际较为贴切。基于改进AASHTO停车视距模型进行强降雨环境车辆制动安全可靠性研究。

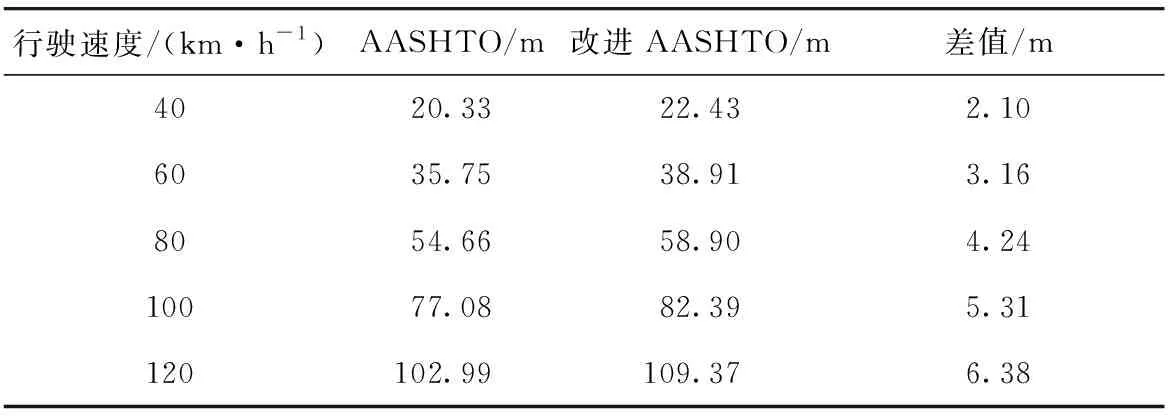
表1 停车视距模型对比Tab.1 Comparison of stopping sight distances

2 强降雨环境制动安全可靠性模型

2.1 功能函数

雨天驾驶员的行车安全主要受轮胎滑水和能见度的影响。在小雨及中雨天气，轮胎滑水对行车安全影响较大。在强降雨天气，能见度对行车安全影响较大，尤其当降雨强度达到3 mm/min时，能见度会低至百米以下，严重影响行车安全[25-28]。当驾驶员发现前方危险进行紧急制动停车时，由于环境-车辆-驾驶员系统许多参数具有随机性，因此，事故的发生是有一定概率的，需采用可靠性方法对车辆的制动安全进行评估。为此，建立系统的功能函数Z≡Z(X)，其中X为系统的随机变量，并规定Z(X)>0为系统处于安全状态，Z(X)=0为系统处于极限状态，Z(X)<0为系统处于失效状态。本研究通过能见度和停车视距建立强降雨环境车辆制动安全可靠性分析的功能函数为：

Z=L-S，

(17)

式中L为雨天能见度。

由于降雨影响，雨天能见度显著降低，其大小与降雨强度有关。雨天能见度如式(18)[29]所示:

L=294.8r-1.1，

(18)

式中r为降雨强度。

车辆在雨天行驶时，雨水会在路面形成一层水膜，进而影响附着系数，雨天路面水膜厚度计算公式为[30]：

hw=0.125 8·l0.671 5·d-0.314 7·r0.778 6·TD0.726 1，

(19)

式中，hw为水膜厚度；TD为构造深度；l为坡面长度(排水长度)，坡面长度l取值可为5 m[30]；d为坡面坡度。根据《公路沥青路面设计规范》(JTG D50—2017)可知，构造深度TD取值可为1 mm；根据《公路工程技术标准》(JTG B01—2014)可知，坡面坡度d取值可为2%。

由于制动过程时间较短，认为车辆在制动时的雨天路面附着系数φ是恒定的。其数值大小可由行驶速度v和水膜厚度hw计算取得[31]：

φ=0.660 3-0.003 7-0.005 7hw。

(20)

通过式(15)，(18)～(20)建立强降雨环境车辆制动安全可靠性分析的功能函数如式(21)所示：

(21)

基于功能函数进行强降雨环境车辆制动安全可靠性及可靠性灵敏度分析。

2.2 可靠性及可靠性灵敏度Monte Carlo模拟

强降雨环境下进行车辆制动安全可靠性评估时，若能见度小雨或等于停车视距，即功能函数Z≤0，认为车辆制动停车时发生碰撞或追尾事故，系统处于失效状态。失效概率Pf如式(22)[32]所示：

(22)

式中，z(x)≤0为失效域；fX(x)为基本随机变量X=(x1,x2,…,xn)的联合概率密度函数。

随机变量的联合概率密度函数在失效域中的积分可以改写为失效域指示函数的数学期望。

E[IF(x)]，

(23)

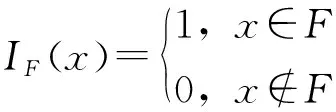
蒙特卡罗模拟方法是将失效域指示函数的数学期望由失效域指示函数的样本均值来近似，以随机变量的联合概率密度函数抽取N个样本点，落入失效域的内样本点个数与总样本点个数的比值即为失效概率的估计值，当样本量足够大时，便可得到精确解。失效概率如式(24)所示：

(24)

式中，xj(j=1,2,…,N)为随机变量的联合概率密度函数抽取的N个样本点，本研究N取107。

可靠性灵敏度定义为失效概率Pf对基本随机变量xn分布参数(均值uxn、标准差σxn等)的偏导数，如式(25)[33]所示：

(25)

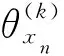
3 计算结果分析

相对于晴天而言，驾驶员在雨天制动停车时,思索时间会有所延迟，延迟时间取值为1 s[34]，即雨天思索时间ta变为2 s，雨天驾驶员制动反应时间t0变为2.2 s，其余各时间段取值与晴天相同。本研究将车速、降雨强度、思索时间建模为随机变量，并假设随机变量X皆服从均值为u，标准差为0.1u的正态分布，基于蒙特卡罗模拟方法计算不同降雨强度(0.5～4 mm/min)下的车辆制动失效概率及失效概率对随机变量均值和标准差的灵敏度。

图2采用确定性方法(即认为车速、降雨强度、思索时间为确定值)计算了不同降雨强度和不同车速下的停车视距值，从图中可以看出，车速越高，停车视距越大，降雨强度越大，停车视距越大。

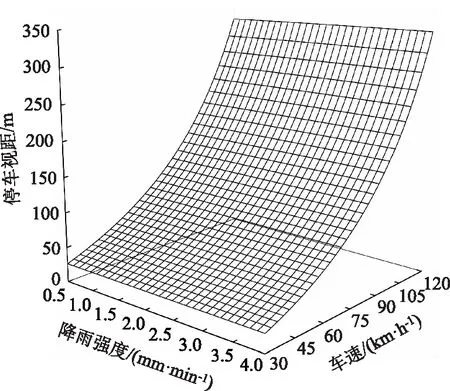
图2 雨天停车视距Fig.2 Stopping sight distance in rainy days

图3以思索时间2 s，降雨强度2 mm/min，车速80 km/h，100 km/h为例，通过随机变量的联合概率密度函数抽取107个样本点，给出了停车视距的统计概率，图中曲线为正态分布拟合曲线。从图3中可以看出，车速的变化对停车视距的波动程度影响较大，当系统的随机变量X服从正态分布时，停车视距也近似服从正态分布，且分布的均值和标准差随着车速的增大而增大。

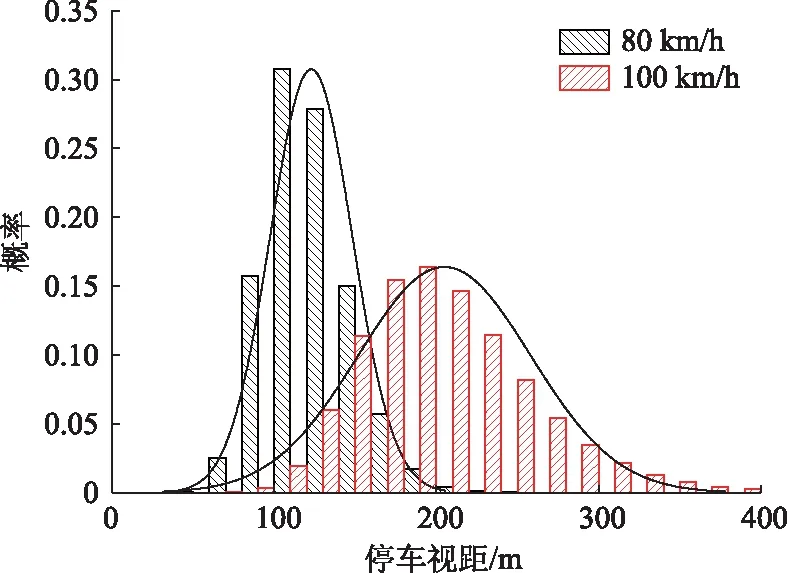
图3 不同车速下的停车视距频率Fig.3 Frequencies of stopping sight distance at different vehicle speeds

图4以思索时间2 s，车速80 km/h，降雨强度1 mm/min，3 mm/min为例，通过随机变量的联合概率密度函数抽取107个样本点，给出了停车视距的统计概率，图中曲线为正态分布拟合曲线。从图4中可以看出，降雨强度的变化对停车视距的波动程度影响较小，对停车视距正太分布曲线均值和标准差的影响也较小。

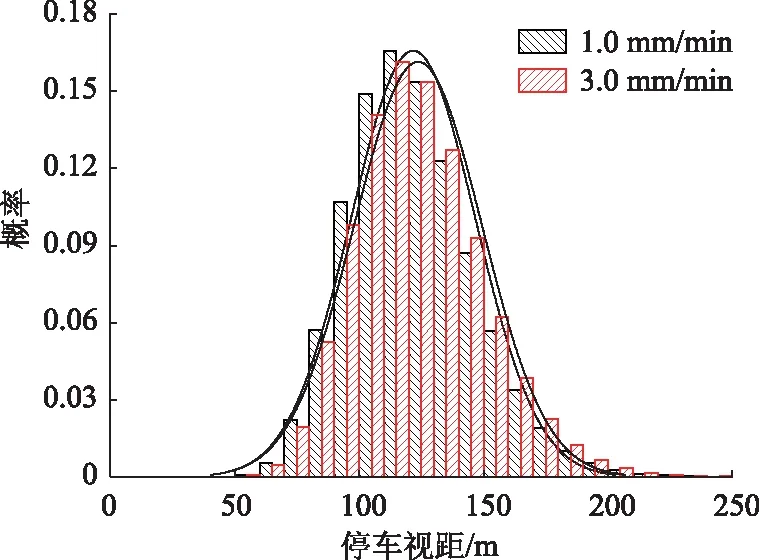
图4 不同降雨强度下的停车视距频率Fig.4 Frequencies of stopping sight distance under different rainfall intensities

图5给出了不同车速、不同降雨强度下的公路车辆制动失效概率。从图5中可以看出，当降雨强度一定时，车速越大，失效概率越大。当车速一定时，降雨强度越大，失效概率越大。失效概率随着车速和降雨强度的增大逐渐接近于1。

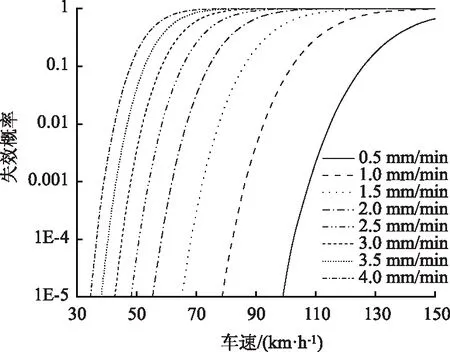
图5 失效概率Fig.5 Failure probability

图6给出了不同失效概率下，车辆在不同降雨强度下的行车安全限速值。从图6中可以看出，采用确定性方法求得的雨天行车安全限速值较为危险，基于可靠性的方法可得到更为合理的雨天行车安全限速值。降雨强度越大，行车安全限速值越低，当给定一个可接受的失效概率，如Pf=0.01，可得到车辆在不同降雨强度下的行车安全限速值。

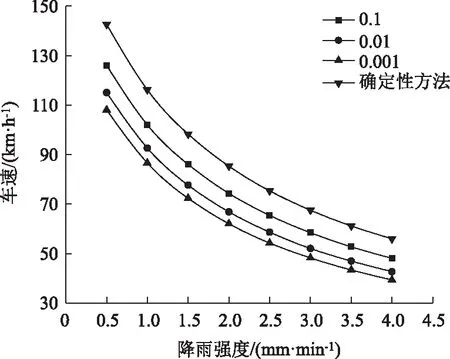
图6 行车安全限速值Fig.6 Speed limit values of driving safety

图7给出了失效概率对随机变量均值的灵敏度。从图7中可以看出，失效概率对随机变量均值的灵敏度存在一个极大值，当降雨强度一定时，随着车速的增大，失效概率对随机变量均值的灵敏度从0开始先逐渐增大，在到达极大值后，开始逐渐减小，最终又趋近于0。降雨强度越大，失效概率对车速均值灵敏度、思索时间均值灵敏度及降雨强度均值灵敏度的极大值点越小，对车速均值灵敏度和对思索时间均值灵敏度的极大值越大，对降雨强度均值灵敏度的极大值越小。

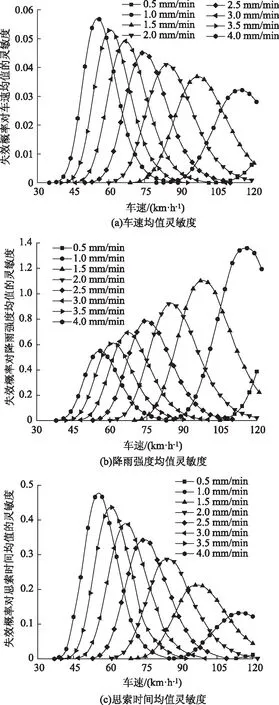
图7 失效概率对随机变量均值的灵敏度Fig.7 Sensitivity of failure probability to mean random variables

图8给出了失效概率对随机变量标准差的灵敏度。从图8可以看出，失效概率对随机变量标准差的灵敏度存在一个极大值和一个极小值，当降雨强度固定时，失效概率对随机变量标准差的灵敏度从0开始逐渐上升，在达到极大值后，又开始下降，并在下降过程中穿过0点，当达到极小值后，又开始上升，最终接近于0。降雨强度越大，失效概率对车速标准差灵敏度、思索时间标准差灵敏度及降雨强度标准差灵敏度的极大值点和极小值点均越小，对车速标准差灵敏度和对思索时间标准差灵敏度的极大值及极小值的绝对值越大，对降雨强度标准差灵敏度的极大值及极小值的绝对值越小。

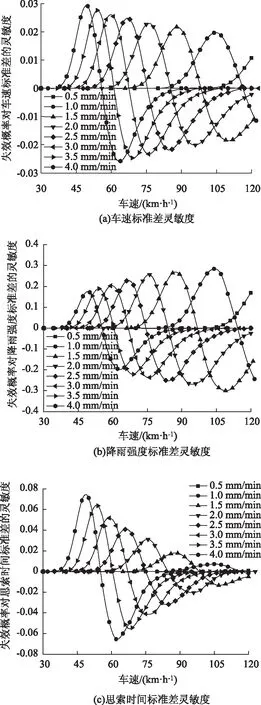
图8 失效概率对随机变量标准差的灵敏度Fig.8 Sensitivity of failure probability to standard deviations of random variables

4 结论

(1)改进AASHTO模型与原始AASHTO模型相比，停车视距计算值偏大，且差值随着车速的增大而增大。

(2)车速的变化对雨天停车视距的波动程度影响较大，降雨强度的变化对雨天停车视距的波动程度影响较小。

(3)车辆在强降雨环境下制动停车时，行车安全限速值随着降雨强度的增大而减小。由传统确定性方法计算得到的雨天行车安全限速值较为危险，基于可靠性方法可得到更为合理的雨天行车安全限速值。

(4)失效概率对随机变量均值的灵敏度存在一个极大值，对随机变量标准差的灵敏度存在一个极大值和一个极小值。