SMA驱动手指康复机器人模糊自适应控制方法研究

王扬威，吕佩伦，郑舒方，王 奔

(东北林业大学 机电工程学院， 哈尔滨 150040)

0 引言

工作压力大和作息不规律，导致上肢神经压迫和脑卒中等疾病不断向年轻化发展，患者神经系统损伤后失去手部运动控制能力[1]，严重影响工作和生活[2]。研究表明康复治疗最有效的方式是基于神经重塑和强化肌肉训练[3]，被动地促使手指重复完成抓握动作，从而改善或修复受损神经。软体手指康复机器人具有动作柔性好、手指契合度高等优点，在手功能康复领域具有广阔的应用前景[4]。

软体手指康复机器人主要采用外骨骼结构，驱动方式主要有绳索驱动[5]、气动驱动[6]和形状记忆合金(shape memory alloy，SMA)驱动[7]等。韩国首尔国立大学研制了一种绳索驱动的硅胶康复机器人[8]，将绳索内嵌于硅胶手套中，依靠绳索收缩带动硅胶手套运动，帮助患者完成抓握物体的动作。德国路贝克大学研制了钢丝绳索驱动的外骨骼康复机器人[9]，该装置采用3D打印结构以适应每个康复患者。钢丝绳用于模拟肌腱，电动机拉动钢丝绳带动外骨骼关节转动，手指随外骨骼运动从而达到康复的目的。绳索驱动结构复杂，刚性外骨骼可能对患者关节造成二次伤害。新加坡国立大学的学者研制了可定制的柔性气动手指矫形驱动器[10]，该装置具有与3个手指关节相应的气动通道，通过气压带动手指弯曲，软体外骨骼避免了对关节的二次伤害，但气动驱动结构的管路和动力源仍较为复杂。SMA丝驱动相比于其他方式具有结构简单、驱动力大、功重比高等优点，已经被广泛应用于软体外骨骼结构致动器[11]。但SMA丝材料的饱和迟滞非线性特性，给精确控制带来了很大的困难[12]。美国Samadi等[13]提出了一种分数阶PID控制器，在传统PID控制器上加入外界环境变量使SMA执行器达到期望的位置，该方法能够消除部分迟滞，但控制器中参数恒定会降低动态性能，影响稳定性。Kilicarslan等[14]采用线性变参数控制器，能一定程度上补偿迟滞问题，但上升时间较长，系统鲁棒性较弱。Zhang等[15]提出神经网络算法对于合金丝模型进行动态逆补偿，将神经网络与PID控制器结合，具有较好的控制精度和鲁棒性，但控制效果过于依靠数据参数的训练结果。稳定性好、响应快的SMA人工肌肉控制算法是提升软体手指康复机器人运动性能的关键。

提出一种用于SMA丝驱动手指康复机器人的模糊自适应控制方法，基于SMA的热力学模型、本构模型和手指康复机器人的运动模型，构建了模糊自适应PID控制策略，实验研究了模糊自适应PID控制器对于软体手指康复机器人的关节角度控制效果，并与传统PID控制效果进行了对比分析。

1 SMA驱动手指康复机器人结构

SMA驱动手指康复机器人由驱动装置(包括上固定板、下固定板、前导丝块、后导丝块和SMA丝)和手部执行机构组成，如图1(a)所示。驱动装置采用SMA丝作为驱动器，由于SMA的应变率约为4%，为保证手指能有足够的屈伸角度，设计了往复式布丝结构以提升收缩量。手部执行机构采用轻量化手套式外骨骼结构，将SMA丝产生的应变转化为外骨骼钢丝绳的移动从而带动手指运动，如图1(b)所示。手指各关节间布置特氟龙导向管充当手指滑车作用，减小钢丝绳与手套式外骨骼之间的阻力，同时避免钢丝在伸展运动中从手指上滑落，保证其在屈曲动作中基本与手指贴合。驱动装置中SMA丝在末端折返形成游动端，手部执行机构中的手指牵引钢丝绳一端固定在下固定板上，另一端穿过SMA丝游动端后固定在指尖，如图1(c)所示。钢丝的移动距离是SMA丝游动端移动距离的2倍，达到在折返SMA的基础上继续增加行程的目的。

2 手指康复机器人驱动模型

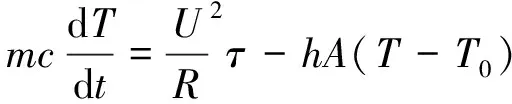
(1)

SMA的相变模型和本构模型定义了材料的热力学特性，即SMA在相变过程中温度、应力、应变的关系，Tanaka模型[16]关系式为：

(2)

E=EA+ξ(EM-EA)

(3)

SMA丝加热过程中，其内部材料由马氏体向奥氏体相变时，马氏体所占的体积分数为：

ξ=exp[a(AS-T)+bσ]

(4)

由奥氏体向马氏体转变过程，即为冷却过程，合金丝内部马氏体所占的体积分数为：

ξ=1-exp[a(MS-T)+bσ]

(5)

式中：AS为奥氏体相变的开始温度；MS为马氏体相变的开始温度；ξ为马氏体百分含量；σ为SMA丝收缩产生的应力；E为SMA相变过程中的弹性模量；EM为SMA处于马氏体的弹性模量；EA为SMA处于奥氏体的弹性模量；Ω为相变的系数；Θ为热弹性的系数；a、b为常量参数，随外界环境改变。

2018年6月23 日上午开幕式，开幕式由呼伦贝尔学院外国语学院院长田振江教授主持。呼伦贝尔学院外国语学院书记金鑫鑫教授和内蒙古大研会会长马占祥教授致欢迎词，各省大研会会长周玉忠教授，董广才教授，李正栓教授，李力教授代表致词，呼伦贝尔学院校方代表陈绍英主任致贺词，论坛常务理事王玫教授提请大家审议通过了2018 NALLTS组委会和学术委员会名单，共有19位专家学者分别担任论坛名誉主席、主席、副主席和执行副主席，有25位各高校外语学院领导成员当选为论坛组委会常务理事。

手指康复机器人单根手指3个关节弯曲角度与合金丝应变收缩距离的关系为：

(6)

式中：x为合金丝的应变收缩位移；l1为近节指骨长度；l2为中节指骨长度；l3为远节指骨长度；θ1为掌指关节(MCP)的弯曲角度；θ2为近端指节(PIP)的弯曲角度；θ3为远端指节(DIP)的弯曲角度，如图2所示。

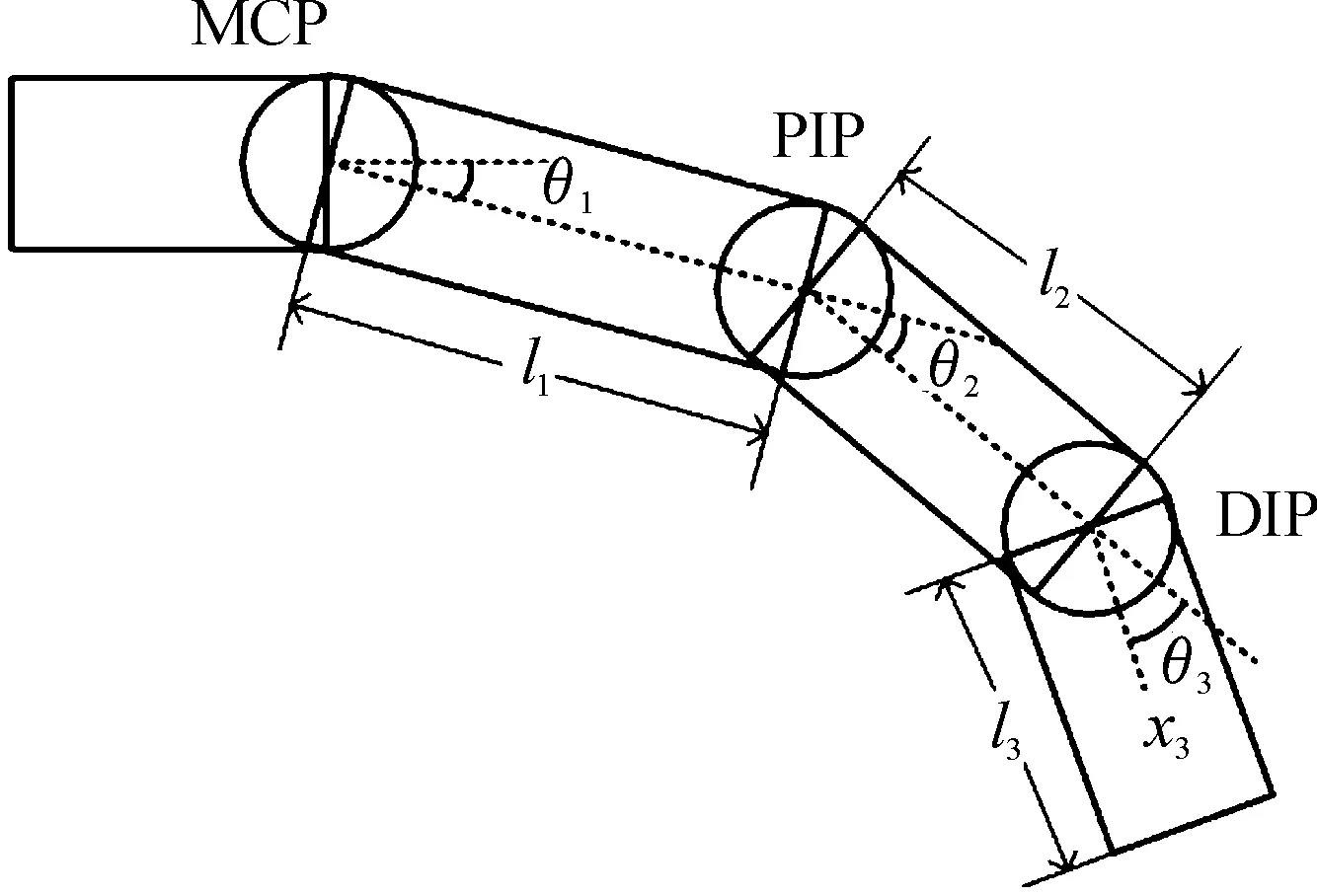
图2 手指弯曲示意图

3 模糊自适应PID控制器设计

3.1 模糊PID控制器结构

SMA材料具有自感知特性，其相变过程中材料电阻与其应变有对应关系。因此，可以利用SMA丝电阻值作为反馈信号[17]，实现对SMA丝应变的控制。SMA材料形变的非线性和迟滞问题使得传统的PID控制算法不能很好地实现位置控制。为此，引入模糊自适应对PID控制参数进行优化，控制器结构如图3所示。输入值U为期望姿态对应的电流，输出值Y为手指的实际位姿对应的电流。

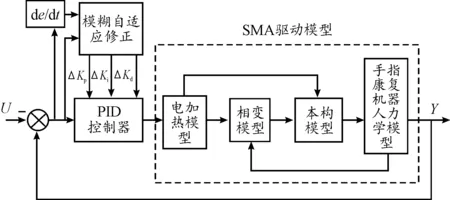
图3 模糊自适应PID控制器工作原理图

3.2 模糊控制器规则建立

根据被控对象SMA丝的驱动特性，采用增量式PID控制器[18]，其离散化处理后表达式为：

(7)

式中:uk为输出量；e(t)为不同时刻的偏差值；Kp、Ki、Kd分别为比例项、积分项、微分项系数。

本系统根据任务设计的模糊控制器由模糊化、模糊推理过程、反模糊化3个部分组成，控制器首先对输入系统中的电流值信号进行模糊化，然后按照预先制定的模糊规则进行运算，最后进行反模糊化，得到实际的控制输出值。

首先对模糊控制器的输入输出进行模糊化，设定模糊控制器中Kp、Ki、Kd的初始参数分别为20、1、0.2，为了规范模糊规则，将输入输出变量转化到同一论域内，为了解决SMA丝的非线性迟滞问题，模糊化子集的隶属度函数选取双边高斯曲线。

模糊逻辑的推理过程在不同外界环境变量下，根据实时测量值与输入量的偏差e以及偏差变化率ec，将两者作为输入变量进行模糊化，从而计算出ΔKp、ΔKi、ΔKd的隶属度和隶属度值，在已定的初始参数基础上进行参数增量调整，最终实现系统模糊自适应控制[19]。

2个输入变量在一定区间内变化，将该区间划分为7个论域，分别用“PB、PM、PS、Z、NS、NM、NB” 分别代表所属的数值的“正大、正中、正小、零、负小、负中、负大”。其中根据输入变量建立的ΔKp、ΔKi、ΔKd的模糊规则如表1—3所示。

反模糊化过程采用面积重心法对模糊输出进行反解，得到该变量实际基本论域内的变化量。

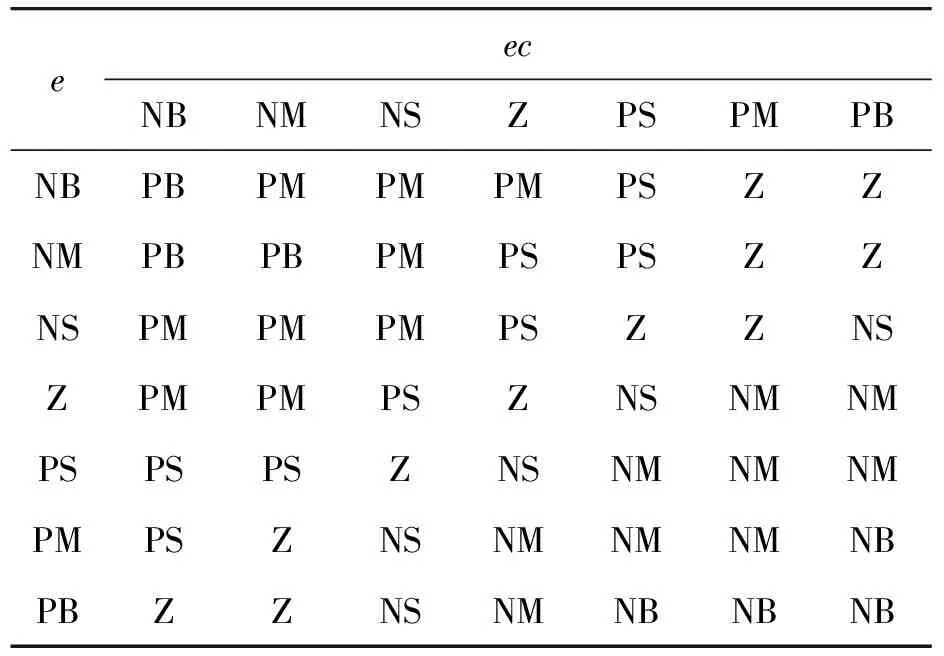
表1 ΔKp的模糊规则表

表2 ΔKi的模糊规则表

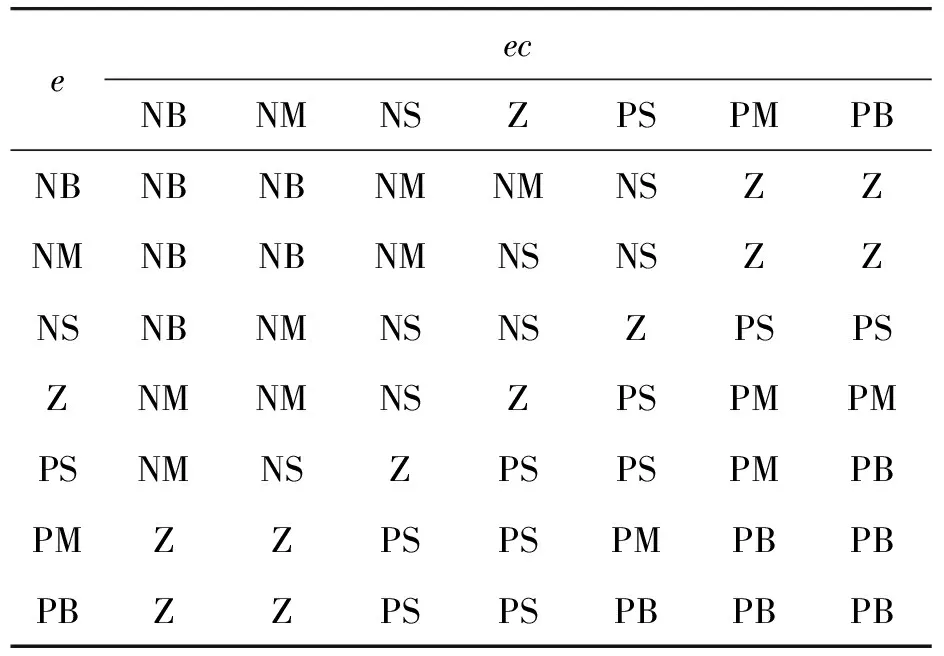
表3 ΔKd的模糊规则表

4 实验结果与分析

4.1 实验台装置

实验装置包括泰信APS3005S可编程直流电源、PC机、STM32F407下位机、ACS712电流传感器模块、驱动板、软体手指康复机器人样机和仿人手模型，软体手指康复机器人弯曲角度变化通过高速相机记录，记录间隔为1 s，PWM脉冲频率为50 HZ，如图4所示。

图4 实验装置图

为了保证手指康复训练试验与实际更加符合，实验中用仿人手模型代替人手进行测试。文献[20]研究表明，手指在不同工作情况下各关节间约束力在一定的范围内，以正常成年人食指为例，远端指节关节的约束力为0～10.5 N，近端指节关节的约束力0～19.4 N，掌指关节的约束力为0～24 N。在仿人手模型忽略摩擦力的情况下，在远端指节和近端指节固定线径0.3 mm，外径0.6 mm，3匝的碳素弹簧钢的扭簧，最大扭力为 12 N。掌指关节固定线径0.4 mm，外径0.8 mm，4匝的碳素弹簧钢的扭簧，最大扭力为16 N，仿人手模型如图5所示，扭簧约束力符合实际情况。

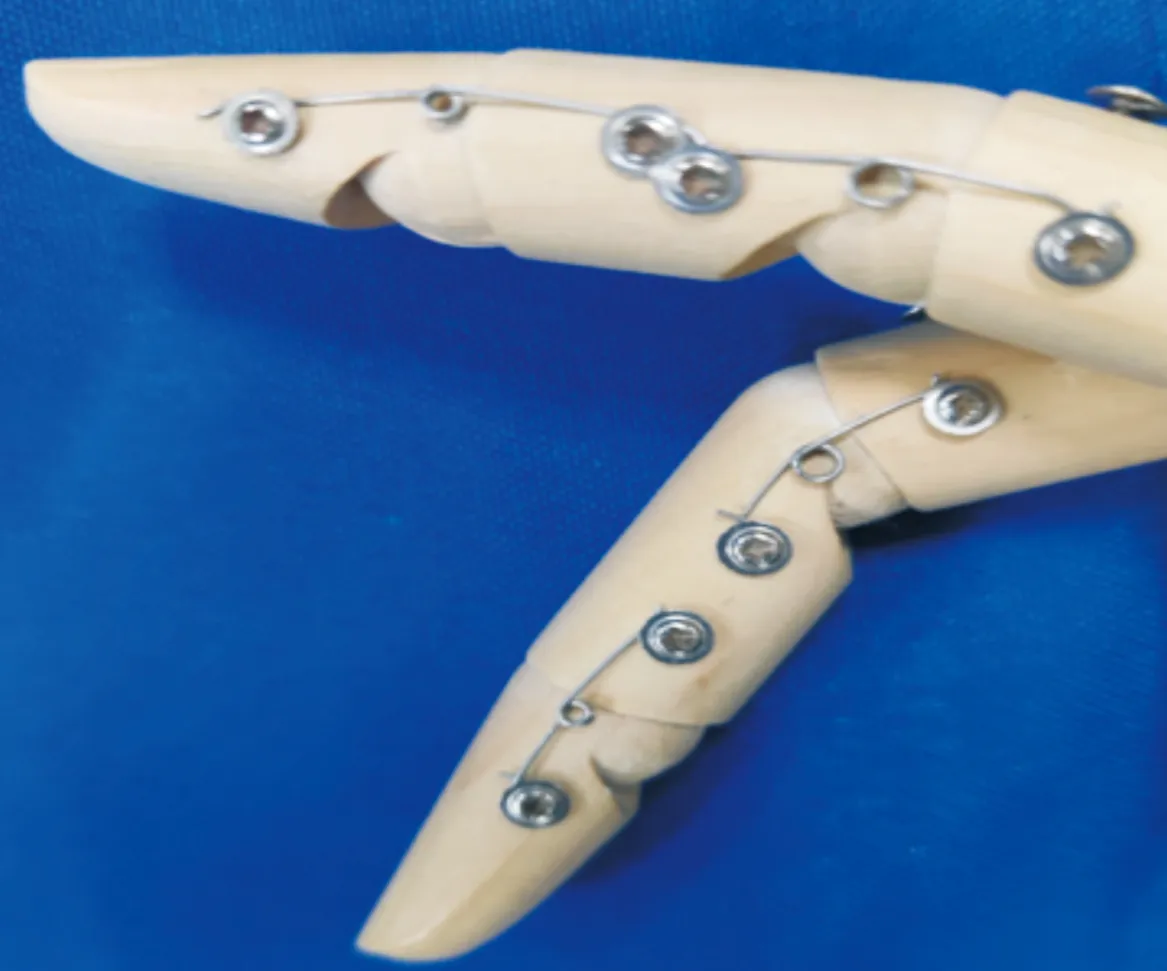
图5 仿人手模型

4.2 软体康复机器人手指关节角度控制

在实验环境温度为25 ℃的条件下，将仿人手模型固定在手指康复机器人上，电源输出设定为恒压24 V。通过控制算法改变合金丝应变量从而控制整根手指的弯曲角度，整根手指达到固定弯曲角度后手指3个关节角度保持稳定，图6为食指弯曲运动序列图。

图6 食指弯曲运动序列图

通过模糊自适应控制算法调整单根手指的弯曲角度以适应不同程度的康复训练，食指弯曲角度与稳定后各关节弯曲角度的关系，见表4。模糊自适应PID和传统PID控制下，食指各关节角度变化的实验结果，如图7—9所示。

表4 食指弯曲角度和各关节角度 (°)

实验结果表明,在食指的远端指节角度稳定后,分别使弯曲角度达到20°、25°、30°、45°，模糊自适应PID分别能在20、17、16、15 s达到期望角度，相比传统PID控制策略响应时间能够缩短2 s，超调量减少了5%；近端指节弯曲角度稳定后弯曲30°、40°、50°、60°，模糊自适应PID分别在18、16.5、16、15 s达到期望角度，相比PID控制响应时间缩短3 s，超调量减少8%；由于掌指关节运动范围受限，稳定状态下角度分别达到15°、20°、30°，模糊自适应PID分别在15、18、17 s达到稳态，相比PID控制缩短4 s，超调量减少9%。

模糊自适应PID控制运动过程中关节弯曲角度变化均匀，能够很好地解决SMA丝驱动过程中的非线性迟滞问题，根据不同情况改变控制参数，具有更短的响应时间和更小的超调量。

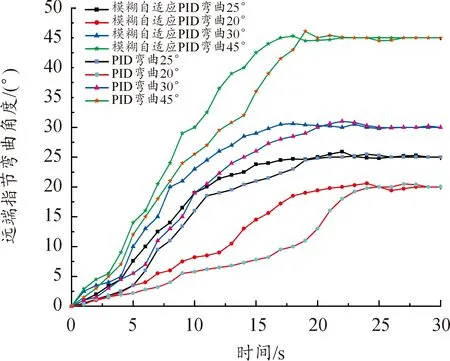
图7 远端指节位置控制曲线

图8 近端指节位置控制曲线

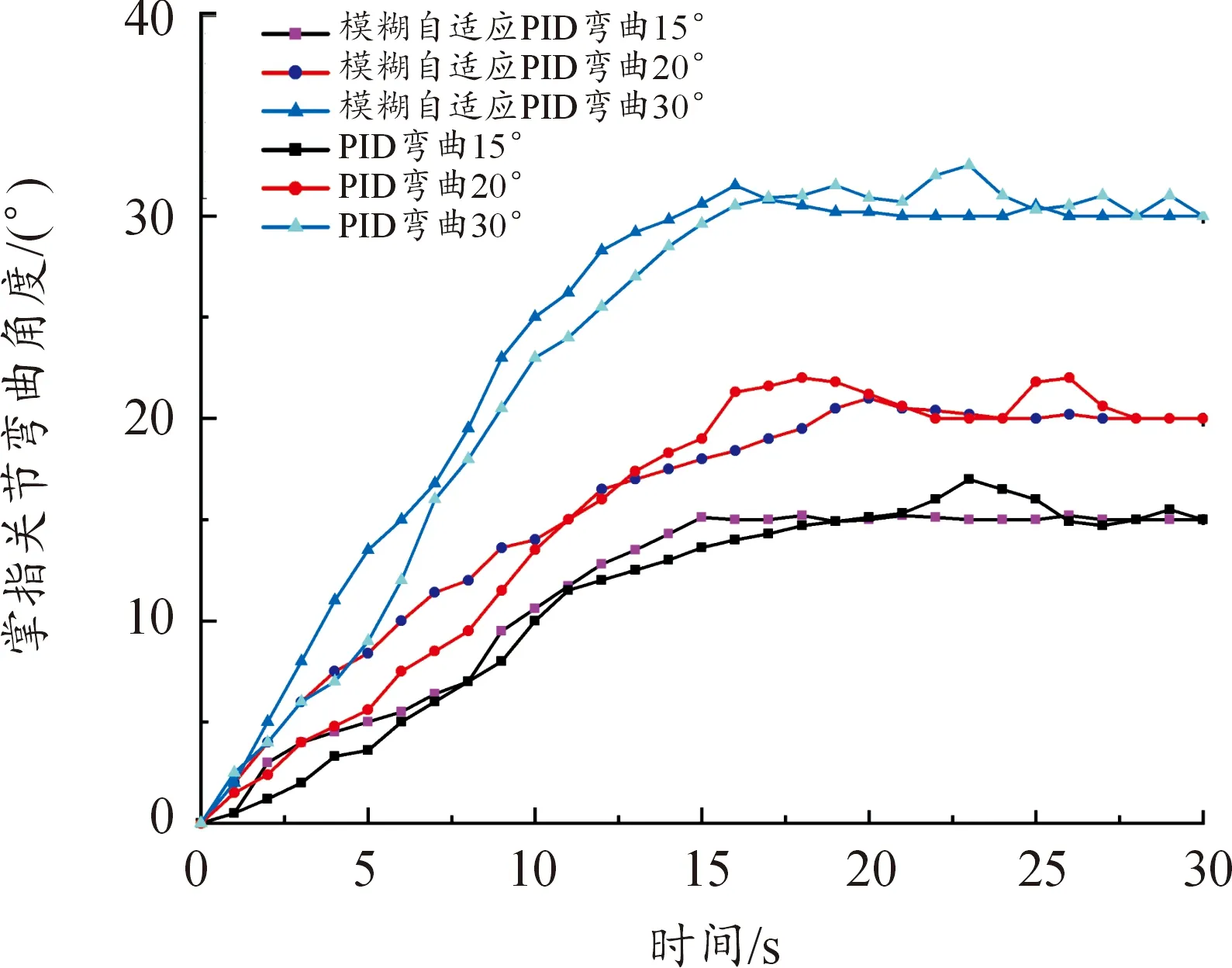
图9 掌指关节位置控制曲线

针对控制系统的鲁棒性进行实验，食指整体弯曲90°(远端指节弯曲30°、近端指节弯曲40°、掌指关节弯曲20°)，当系统处于稳定状态下，在20 s时分别在指尖附加50、100、150、200 g的砝码充当外部负载，如图10所示。手指关节角度变化的实验结果，如图11—13所示。结果表明，通过模糊自适应PID控制系统在远端指节处于稳定位置状态下，附加50、100、150、200 g负载下分别下降了3°、5°、7°、9°，在系统自适应调节后2、4、5、6 s后恢复到稳定角度，相比于PID控制，恢复时间平均提高了2～3 s。

近指关节在不同负载下分别下降了4°、6°、8°、10°，在3、4、6、7 s后恢复到稳定位置，相比PID控制，时间缩短了3～5 s；掌指关节在负载作用下下降了2°、6°、7°、9°，在3、4、5、7 s后恢复稳定，恢复时间相比于PID提高了3～5 s。

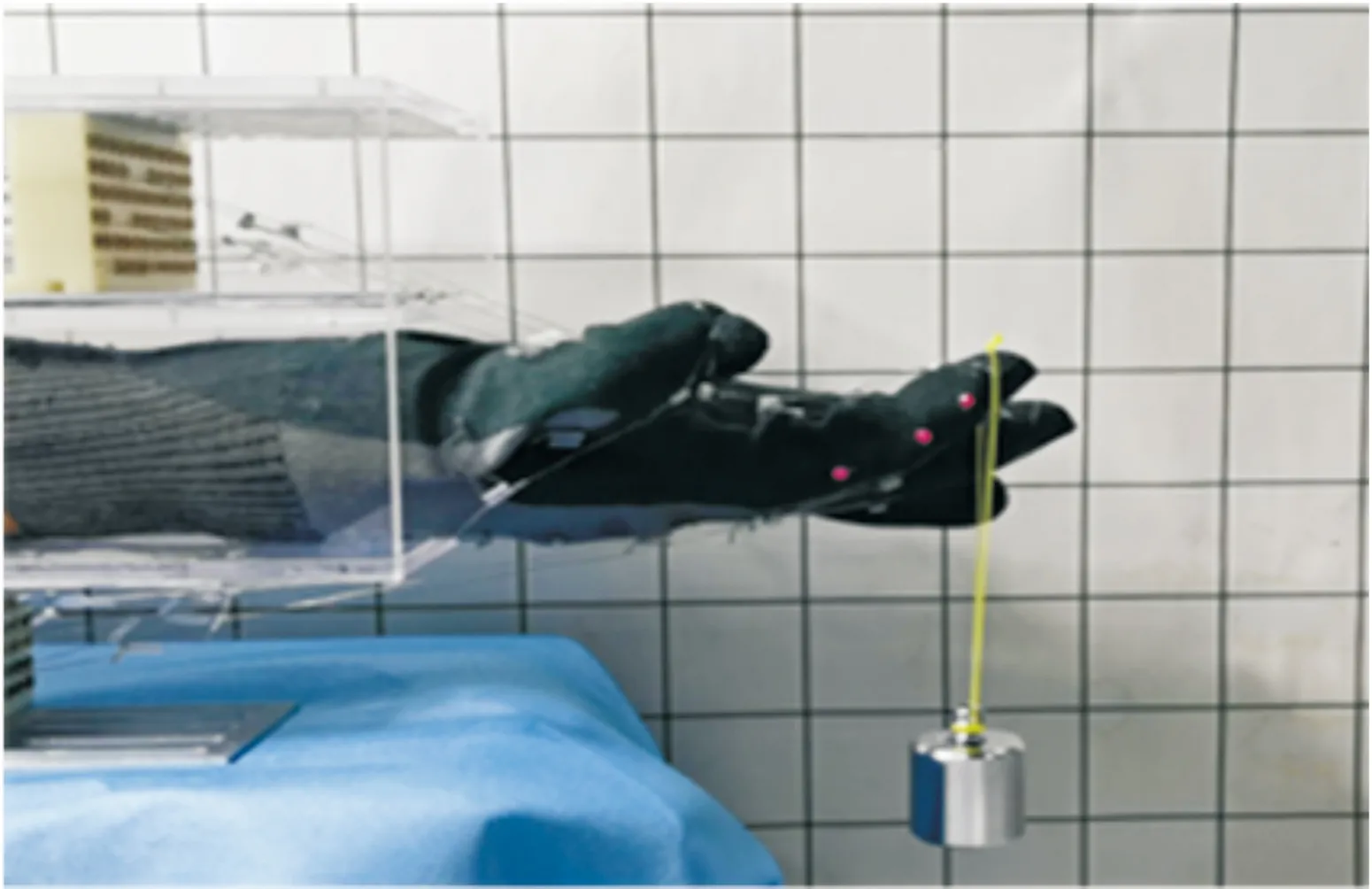
图10 稳定状态下负载实验图

图11 远端指节负载回复图

图12 近端指节负载回复曲线

图13 掌指关节负载回复曲线

实验结果表明，模糊自适应PID控制算法相比于PID控制具有很强的鲁棒性，在有外部环境干扰的情况下，能够通过推论改变最优的参数，使整个系统在短时间内恢复稳态，且误差范围小。

5 结论

针对SMA丝驱动外骨骼式手指康复机器人屈伸角度难以精确控制的问题，提出了一种模糊自适应的控制算法，对于食指关节角度进行定量控制。实验研究表明，模糊自适应PID算法相比于PID达到稳态时间提升2～3 s，超调量平均降低9%，稳定状态下具有更好的鲁棒性，能够明显消除SMA丝的迟滞问题。