基于STSS模型的改进及其应用

匡 婵,郑海涛,赵宜婵,韦洪雷

(西南交通大学 数学学院， 成都 611730)

0 引言

随着信息技术的迅猛发展和大数据时代的到来，以环境、交通、金融、医疗等为代表的多个领域产生大量数据，这些数据中蕴含着丰富的时空信息。例如医学成像数据[1]、环境监测卫星遥感数据[2-3]、国家环境信息中心数据集NCEI(national centers for environmental information)等。针对不同类型的时空数据，需要找到合适的表达来描述数据反映出的各项信息。而采用合适的模型来对不同类型的时空数据进行分析，会提高对时空特性探究的准确度，以及对数据变化趋势有更真实的描述，这对时空数据的应用发展有着重要的意义。

近年来，国内外关于不同类型时空数据的应用研究都是比较频繁的。例如，Cabrera等[4]通过广义加性混合模型建立时空数据模型来观察天气和登革热传播之间的复杂关系，这项研究汇集了来自不同来源的大型数据集，包括委内瑞拉卫生部，还包括美国国家航空航天局提供的远程卫星气候数据。再例如，Ghosh等[5]提出了一个端到端的交通关联规则挖掘框架，通过分析城市的出租车出行轨迹，有助于提取城市交通动态，此研究使用NYC绿色和黄色出租车跟踪、罗马出租车数据集和旧金山出租车数据集的真实GPS跟踪数据集，属于轨迹数据类。而许熳灵等[6]也同样使用轨迹数据，他们基于智能交通卡数据，以南京市为例，通过建立一种季节性差分自回归移动平均模型，解释了不同种类的天气因素(如降雨、气温、相对湿度、风速等)对地铁客流量时空分布的影响程度。

对于收集到的一些海量的、有噪声的数据进行平滑处理是了解其时空特征的关键。例如，对于NARCCAP(the North American regional climate change assessment program)[7-8]这样的大规模时空数据集，French等[9]提出了一种平滑处理方法STSS(spatio-temporal sandwich smoother)。在2013年Xiao等[10]提出的OSS(the original sandwich smoother)的基础上，发展了一种惩罚样条方法来表示具有主光滑成分的连续时空数据，分别对空间和时间维度采用不同的基函数来进行处理，他们还用模拟和实际数据证明了此方法的实用性。French等提出的STSS模型不仅能在保留数据时空特性下对数据做平滑处理，还具有高效的计算效率。而NCEI收集到的数据集不仅具有大规模的特性，还包含各种不同的信息变量。针对呈现出多维信息的时空数据，需要合适的表达来描述这类时空数据的特征。

French等提出的STSS模型能在时间、空间上捕捉到关键特征，但当协变量对响应有影响且有周期特征时，STSS模型还是不能很好地解释数据的变化。因此，引入了协变量函数和周期函数。协变量函数用来描述各种信息变量对响应变量的影响，而周期函数用来补偿解释数据的周期性。利用STSS模型关于基函数和惩罚函数的运用，可以对大规模数据进行平滑处理；同时还伴随着协变量和周期性对观察变量的影响。关于协变量函数使用的是常见的多元线性模型，而周期函数则考虑了不同周期长度的描述，这样能探究出数据更真实的周期变化。为了更好地处理上述类型的时空数据，提出的模型不只是单一地讨论数据的时空结构，也可以观测其相关信息对数据变化的影响，还包括探测数据变化是否具有一定的周期性，这样的结合使得所提的模型能更全面、更贴合实际地描述时空数据的结构和变化。

论文的结构如下：第1节介绍了所提出的改进模型，包括模型的表达形式和参数估计方法；第2节利用蒙特卡洛的方法对所提出的模型进行了模拟研究；第3节将改进模型应用于实际时空数据集，并对分析结果进行了讨论；第4节对所提出的方法进行了总结。

1 模型介绍

对于一些数据集，它们收集的区域范围广，统计年份长，呈现出大规模的数据集，还包含着多种信息变量，并且数据变化存在明显的周期性。而期望能在对数据做平滑处理的同时，还能观察一些相关因素对数据的影响和数据的周期变化情况，因此在French等提出的STSS模型基础上，引入了协变量函数和周期函数。关于描述协变量与响应变量之间的关系使用的是常见的多元线性模型，周期函数则也考虑了不同周期长度的描述。下面是关于模型的具体介绍。

1.1 模型表达

假设在某个区域内观测到n1个不同地点和n2个不同时间的响应，用数学模型可表示成

yij=y(xij;si,tj)=

f(xij)+d(tj)+z(si,tj)+ε(si,tj)，

i=1,2，…,n1,j=1,2，…,n2

(1)

其中：y是响应变量，f(x)是有关影响y的协变量x的函数，d(t)是关于时间t的周期函数，z(s,t)是考虑成空间位置s和时间t对y的一个影响，误差过程ε(s,t)满足Ε(ε(s,t))=0，Ε(ε2(s,t))=σ2。如上文所述，考虑f(x)是关于x的多元线性函数，z(s,t)则是使用STSS模型的方法，即空间基函数和时间基函数的张量积，令

其中：p是协变量的个数，C是一个由周期函数构成的矩阵，残差εij=ε(si,tj),1≤i≤n1,1≤j≤n2，这里的周期函数d(t)可以采用如下形式：

(2)

其中：α1,α2,…,α2k-1,α2k是函数的系数，2k是周期函数的个数，m1,m2,…,mk取值为正整数。在应用于实际数据的时候，可以综合考虑周期呈半年、季度以及月度等的变化来确定k和m1,m2,…,mk的取值，以便观察数据更真实的周期性。则周期函数矩阵也可以表示成

则上述数学模型(1)可以表示成矩阵的形式：

y=Xβ+Cα+Bθ+ε

(3)

式(3)中，基函数的张量积B=B2⊗B1，其中B1、B2分别是关于空间和时间的基函数矩阵，具体形式如下：

其中：rk(si),1≤k≤c1,1≤i≤n1是描述空间的径向基函数，bl(tj),1≤l≤c2,1≤j≤n2是描述时间的B样条基函数。

这里采用的径向基函数是Wendlend协方差函数[11]，基本形式为：

其中：k=1,2,…,c1，h=|ki-s|是空间中2点之间的距离，ki,i=1,2,…,c1表示空间节点，N是多项式阶数，φ是函数的支撑(也称带宽参数)，aj,j=1,2,…,N为一组非零系数。关于Wendland协方差函数的更多细节可以在文献[11-12]中找到。采用的B样条基函数的一个递归定义[13-14]如下，设τ0≤τ1≤…≤τM为一组时间节点，记第i个d次B样条基函数为Bi,d(t)，定义

其中i=0,1,…,M-1。当节点数M和次数d确定时，得到一组B样条基bl(t),1≤l≤c2，其中c2=M+d+1。

1.2 参数估计

在给定的惩罚参数λ1、λ2下，关于上述模型(3)的目标函数可表示为：

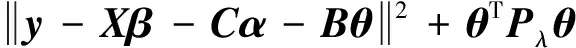
(4)

其中

λ1λ2(Dm)TDm⊗(Sm)TSm

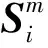
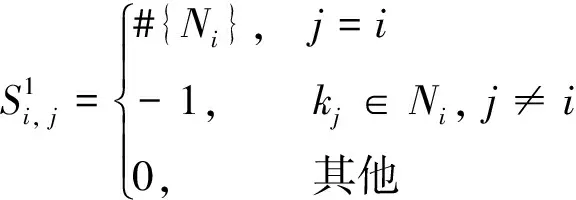
其中#{Ni}为近邻集Ni元素的个数；当m≥2时，定义

则依次计算出Sm的每一行元素。关于空间差分矩阵更多的运用细节可以在French等的文章中找到。惩罚参数λ1、λ2可通过广义交叉验证[15-17]的方法进行选择。

令参数

q是周期函数系数的个数，根据1.1小节的描述可知q=2k，则上述目标函数(4)可以转化为以下形式：

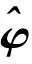
(B,X,C)Ty

2 模拟研究

根据所提出的模型随机生成数据，然后进行多次模拟，来观察其参数估计的结果、模型拟合的效果以及模型残差的分析结果，模拟设置如下：

1) 样本容量n=n1×n2×n3，n1、n2是关于空间位置的样本大小(一共有n1×n2个空间位置)，n3是时间长度的样本大小。模拟取5×5个空间点，分小样本n=5×5×50、中样本n=5×5×200和大样本n=5×5×500。

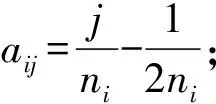
3) 根据2得到空间维和时间维的基函数矩阵B1、B2和差分矩阵Sm、Dm；确定周期函数矩阵，模拟将周期矩阵设置为：

由上述的模拟设置，在不同的样本容量和标准差的情况下，各进行了1 000次的重复模拟，最后取每个参数估计结果的均值。与参数模拟取值的比较如表1—3所示，从估计结果看，取不同大小的样本容量以及不同的标准差，得到的估计值与模拟取值相差都比较小。模拟数据的周期函数系数仅α1、α2取值不为零，其余的周期系数均取值为零，而其余的周期函数系数α3、α4、α5和α6的估计都非常接近于0，则可以说明周期项得到的估计结果与模拟数据周期项也非常相近，即可以说明提出的模型能反映数据的真实周期变化。参数估计结果的均方差(MSE)如表1—3括号中的数值所示，表中数据显示随着样本容量的增加均方差在逐渐减小，而随着标准差取值的增加均方差也在增加，其各均方差值也都比较小，表示参数估计结果的波动比较小。

表1 小样本模拟数据参数估计结果

表2 中样本模拟数据参数估计结果

表3 大样本模拟数据参数估计结果

任意选取一个空间位置，在3种样本大小和3种标准差的情况下，分别观察模型的拟合效果。图1是同一空间位置的观测值与拟合值，其中红色实线为观测值，绿色虚线为拟合值。如图1所示，可以看到图中的拟合效果都是比较好的，而随着标准差取值的增加会使得其拟合值与观测值之间的差变大。从任一位置的拟合图形可以看到，不管是小样本、中样本还是大样本，其模型的拟合效果都是非常好的，随着标准差取值的增加，观测值的波动会稍微变大，而拟合值会相对平滑一些。此外，还对任一空间位置进行了残差分析，结果显示不同样本不同标准差情况下的残差都呈现出非常好的随机性和正态性。各种残差图形以及正态性检验结果如图2—4和表4所示，表4中显示检验的P值均大于0.05，可判断残差服从正态分布。也就意味着所提出的改进模型有较好的适用性，下面通过实际数据的应用来证实模型的实用性。

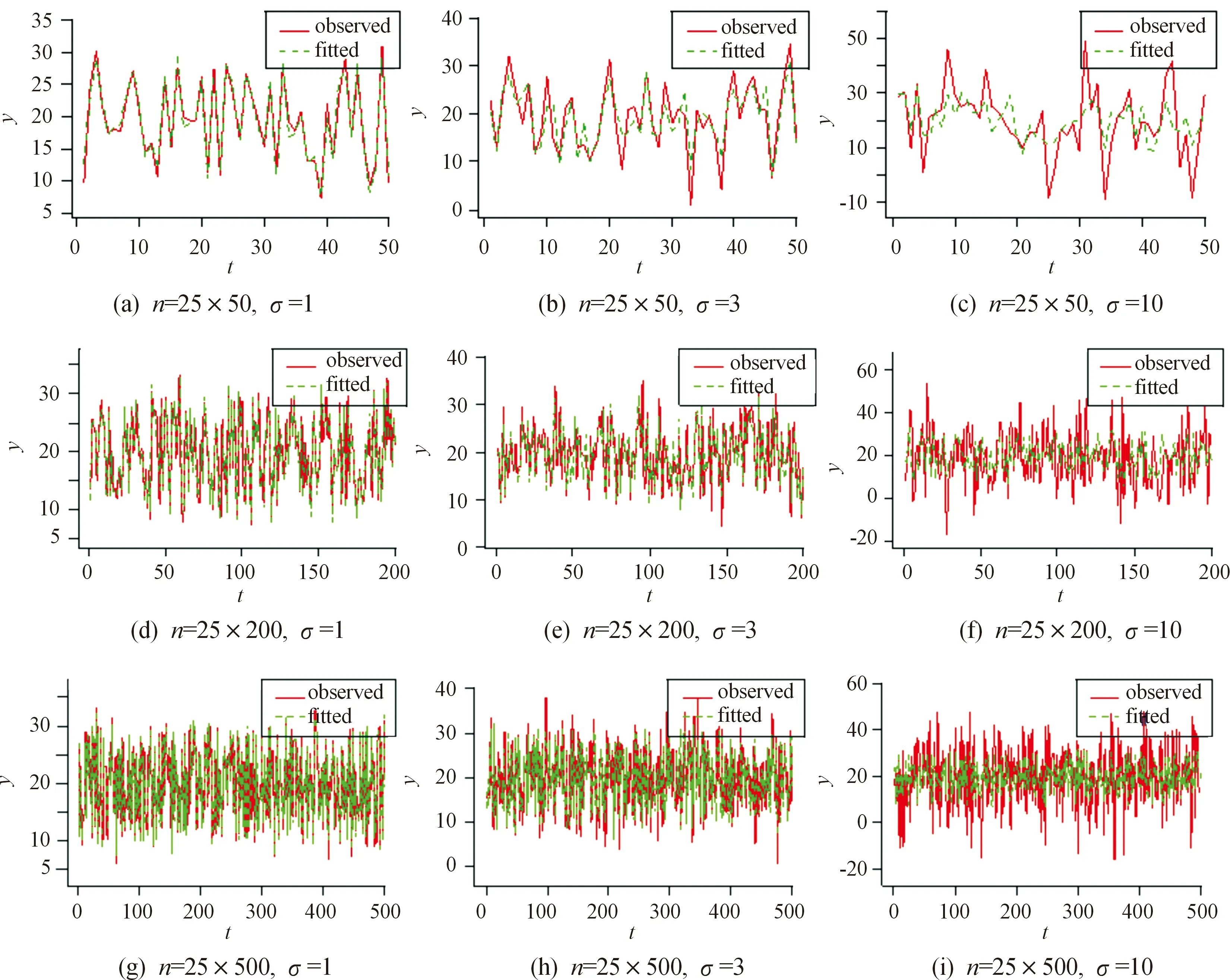
图1 3种样本容量不同标准差下的拟合图

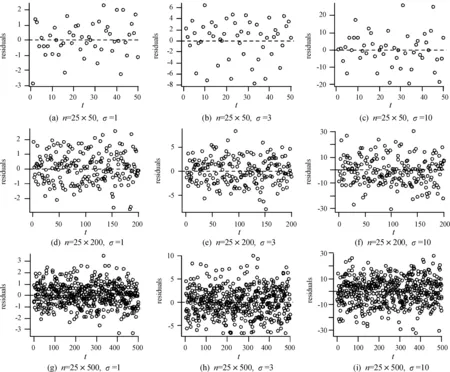
图2 3种样本容量不同标准差下的残差图

图3 3种样本容量不同标准差下的残差Q-Q图

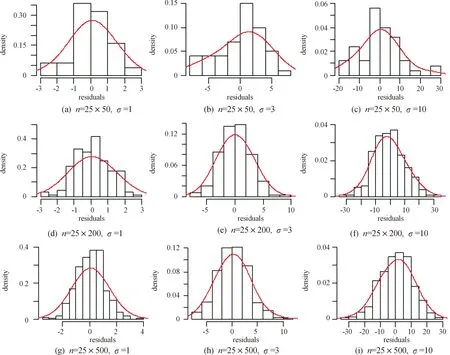
图4 3种样本容量不同标准差下的残差直方图

表4 残差的正态性检验(Kolmogorov-Smirnov)结果

3 案例分析

在这一节中将用上述改进的模型应用于实际时空数据，并与STSS模型做比较。实际应用的时空数据是由NCEI收集的数据集。随机选取美国的Colorado州中57个站点的月平均温度(华氏度)数据，将此作为待观测的响应变量，其中各个站点的空间位置由经纬度表示，时间长度为从2000年1月到2020年12月，形成了252个月份内在57个空间位置观测到的时间序列，总共有14 364个响应值。图5中的黑色圆点表示各个站点的位置。其余的信息变量还包括各个站点的海拔和月降水量，将这2个信息变量作为待观测数据的协变量。

现在考虑将改进的模型应用于这些数据。在关于基函数的处理上，空间维度使用2种不同分辨率下的Wendland协方差函数，分别使用4节点和20节点(共24个节点)，每个分辨率的节点位置在图5(b)中用不同颜色和形状的符号表示，采用m=2阶的空间差分惩罚；时间维数使用了12个B样条基函数。为了能更准确地抓住数据的真实周期变化，这里考虑设置周期函数的个数为q=16和正整数取值(m1,m2,…,m8)=(2,4,6,8,10,12,24,36)。

图5 Colorado州中57个站点的位置

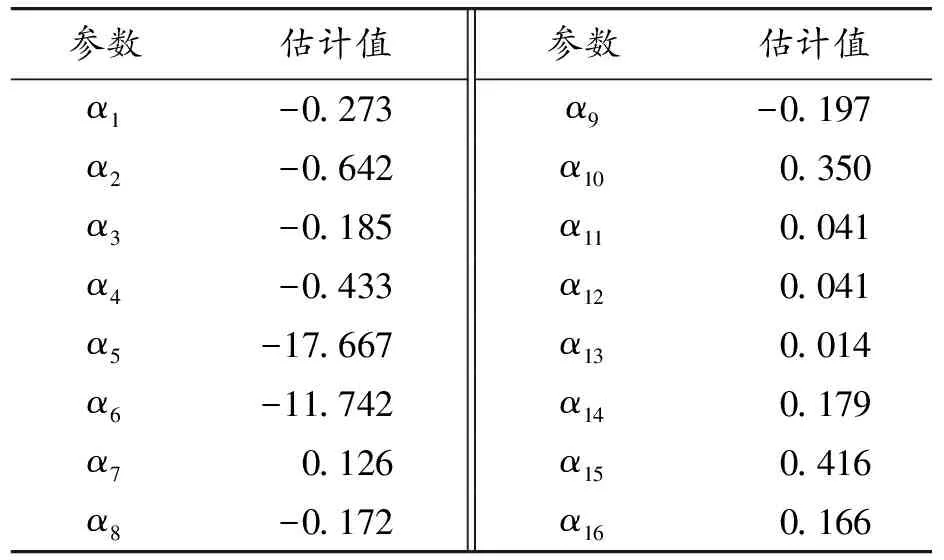
表5 周期函数参数估计结果

接下来将观察模型的拟合效果和残差分析。图6是选取的任一站点位置的拟合图，图中红色实线为月平均温度的真实观测值，绿色虚线为拟合值。从图6可以看到2条线非常贴合，说明模型的拟合效果是很不错的。图7是整体残差的相关图形，图7 (a)是整体残差图，图7 (b)是残差直方图，残差图中的数值大致均匀分布在零均值线上下，从图7可以看到,整体残差的随机性和正态性都表现得很好，说明模型适用于实际时空数据。

图6 任一站点位置的拟合图

图8 观测到的月平均温度(华氏度)和拟合值的散射图

表6是2个模型的均方差比较，从表中数值可以看出，改进模型的均方差比STSS模型小很多，说明改进的模型要比STSS模型更适合于时空数据。图8分别是2个模型的拟合数据和观测数据的散射图，其中图8(a)是STSS模型，图8 (b)是本文模型的散射图，显示了变量之间期望的线性关系，可以看到改进的模型比STSS模型能更完整地捕获原始月平均温度数据的总体模式。

表6 模型的均方差

French等提出的STSS模型具有高效的计算效益和很好的数据结构捕获效益，但也提到在应用STSS模型时，会因为模型中的一些调整参数的不同设置导致模型得到的结果存在差异。例如，基函数的节点数，太少会导致拟合结果过于平滑，但节点数太多又会使得基函数的参数增多从而使得计算量增大；再比如，带宽参数φ的选择，French等建议至少是每个节点与其近邻点之间最大距离的2倍，但φ太大也会导致计算不稳定，因为生成的基函数矩阵将具有高度相关的列。还有基函数的阶数、差分矩阵的阶数m，等等。也就是说，在应用于实际时空数据的时候，有时会因为一些原因使得模型的这些调整参数不一定取到最合适的数值，这样会很容易降低模型的使用效益，也会减少模型的实用性。而从图8(a)和图8(b)的对比结果可以看到，提出的改进模型会大大减少这种情况对结果产生的影响，能在一定程度上有效地保证模型的使用效益，从而确保模型的实用性。

4 结论

在French等提出的STSS模型基础上进行了改进，使其更适用于包含多维信息的大规模时空数据。在STSS模型上引入了协变量函数和周期函数，协变量函数描述各信息变量对观察变量的影响，周期函数描述数据的周期性。其中关于协变量与观察变量之间的关系使用的是常见的多元线性模型，而周期函数则考虑了不同周期长度的描述。与STSS模型相比，所提的改进模型既能在保留时空结构下对数据做平滑处理，还可以观测其相关因素对数据的影响，探测数据变化的周期性。然后通过模拟实验和NCEI收集的实际时空数据应用验证了改进模型的适用性和实际性。

模拟研究结果表明，改进的模型呈现较好的拟合效果，而随着数据标准差取值的增加，观测值的波动稍微变大，模型的拟合更趋于平滑。此外，模型的残差在各种情况下都呈现良好的正态性，即显示了改进的模型有很好的适用性。将改进的模型应用于实际时空数据，分析结果呈现了良好的拟合效果，显示了改进模型的优良性。与STSS模型进行对比，改进的模型比STSS模型能更完整地捕获原始数据的整体变化。